Τα βασικά του Centroid
Είναι σημαντικό να σημειωθεί ότι σε μια διατομή, του οποίου η περιοχή είναι ομοιόμορφη παντού, το κεντροειδές μπορεί να βρεθεί λαμβάνοντας το άθροισμα των στιγμών σε σχέση με έναν άξονα που έχει ρυθμιστεί αυθαίρετα, αλλά συνήθως τοποθετείται στην κορυφή ή στην κάτω ίνα. Δείτε το προηγούμενο άρθρο μας για υπολογισμός του κέντρου τμήματος δοκού και SkyCiv Free Centroid Calculator.
Βασικά, το κεντροειδές μπορεί να ληφθεί λαμβάνοντας το άθροισμα των στιγμών κατά το άθροισμα της περιοχής. Αυτό εκφράζεται με αυτόν τον τρόπο.
[μαθηματικά]
\μπαρ{Χ}= frac{1}{ΕΝΑ}\int xf αριστερά ( x δεξιά )dx
[μαθηματικά]
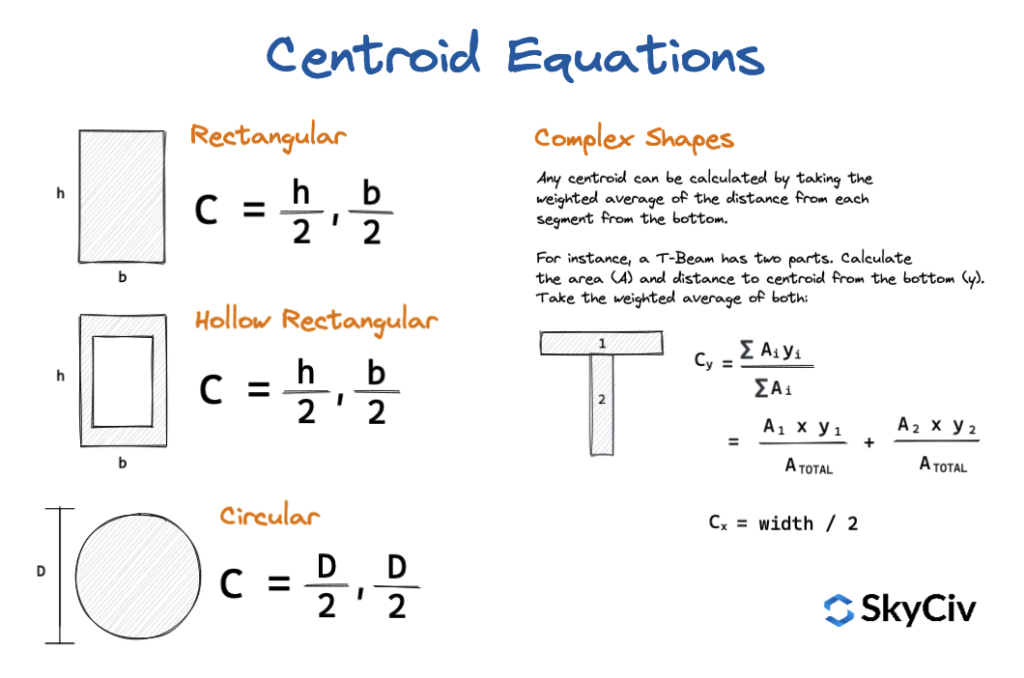
Περίληψη Centroid Equations
Στην παραπάνω εξίσωση, φά(Χ) είναι η συνάρτηση και το x είναι ο βραχίονας στιγμής. Για να το διευκρινίσω καλύτερα, θα αντλήσουμε το κεντροειδές y ενός αυθαίρετου τριγώνου με τη βάση του να συμπίπτει με τον άξονα x. Σε αυτή την κατάσταση, το σχήμα του τριγώνου, είτε είναι ισόπλευρη, Τα ισοσκελή ή το σκαλένιο δεν έχουν σημασία, καθώς όλα σχετίζονται μόνο με τον άξονα Χ. Σημειώστε ότι το σχήμα δεν έχει σημασία εάν η βάση του τριγώνου είναι σύμπτωση ή παράλληλη σε σχέση με τον άξονα. Αυτό δεν θα συμβεί κατά την επίλυση του x centroid. αντι αυτου, μπορείτε να το φανταστείτε ως λήψη του κεντροειδούς δύο σωστών τριγώνων σε σχέση με τον άξονα y. Για λόγους ευκολίας, ας φανταστούμε ένα ισογώνιο τρίγωνο παρόμοιο με τον παρακάτω πίνακα αναφοράς. Η εύρεση της σχέσης μεταξύ b και h θα δώσει την ακόλουθη σχέση.
[μαθηματικά]
\frac{-και}{Χ}= frac{-η}{σι}
[μαθηματικά]
Σημειώστε ότι η κλίση είναι αρνητική καθώς φαντάζουμε το τρίγωνο να είναι όρθιο. Αν φανταστούμε το τρίγωνο να αντιστραφεί, η κλίση θα ήταν θετική. Ανεξάρτητα, η σχέση παραμένει η ίδια. Ως x = f(και), Η παραπάνω σχέση μπορεί να ξαναγραφεί ως εξής.
[μαθηματικά]
x = f αριστερά ( σωστά )= frac{σι}{η}και
[μαθηματικά]
Μπορούμε τώρα να λύσουμε το centroid. Προσαρμογή της πρώτης εξίσωσης παραπάνω, έχουμε τα ακόλουθα.
[μαθηματικά]
\μπαρ{και}= frac{1}{ΕΝΑ}\int yf αριστερά ( σωστά )δύο
[μαθηματικά]
Η σύνδεση πρόσθετων τιμών και η αντικατάσταση της παραπάνω σχέσης θα αποφέρει την ακόλουθη εξίσωση.
[μαθηματικά]
\μπαρ{και}= frac{2}{βχ}\int_{0}^{η} \frac{σι}{η}και ^{2}δύο
[μαθηματικά]
Απλοποίηση,
[μαθηματικά]
\μπαρ{και}= frac{2}{h ^{2}}\αριστερά [ \frac{και ^{3}}{3} \σωστά ]_{0}^{η}
[μαθηματικά]
[μαθηματικά]
\μπαρ{και}= frac{2}{h ^{2}}\αριστερά [ \frac{h ^{3}}{3}-0 \σωστά ]
[μαθηματικά]
[μαθηματικά]
\μπαρ{και}= frac{2}{3}η
[μαθηματικά]
Σημειώστε ότι αυτή η λύση έχει ληφθεί από την κορυφή. Το κεντροειδές που λαμβάνεται από το κάτω μέρος πρέπει τότε να είναι ίσο με 1/3 του h.
Formula for centroids of common shapes and beam sections
Παρακάτω είναι μια λίστα με α ποικιλία σχημάτων τομής δοκού και την απόσταση από τα κεντροειδή του τμήματος. Οι εξισώσεις δείχνουν πώς να βρείτε το κεντροειδές μιας συγκεκριμένης ενότητας από τη βάση ή το πιο μακρινό αριστερό σημείο της ενότητας. Για συνδρομές SkyCiv Student και Structural, αυτή η αναφορά μπορεί επίσης να ληφθεί ως αναφορά PDF για να πάρετε μαζί σας όπου κι αν πάτε. Τα κεντροειδή του τμήματος δέσμης είναι εξαιρετικά σημαντικά καθώς εντοπίζουν τον Ουδέτερο Άξονα και είναι ένα από τα πρώτα βήματα που απαιτούνται κατά την ανάλυση ενός τμήματος δέσμης.
Το SkyCiv προσφέρει επίσης έναν περιεκτικό πίνακα περίληψης τμημάτων που περιέχει όλες τις εξισώσεις και τους τύπους που σχετίζονται με τις διατομές δοκών (στιγμή αδράνειας, περιοχή κ.λπ.…).
Η εξίσωση για διάφορα κεντροειδή αναφέρεται παρακάτω:
| ΑΝΑΦΟΡΑ | ντοκαι (Απόσταση από κάτω) |
ντοΧ (Απόσταση από το πιο μακρινό αριστερό σημείο) |
Κεντροειδές ορθογώνιο ή ορθογώνιο τμήμα |
||
|---|---|---|
 |
[μαθηματικά] \dfrac{η}{2} [μαθηματικά] |
[μαθηματικά] \dfrac{σι}{2} [μαθηματικά] |
Κεντροειδές ενός κοίλου ορθογώνιου τμήματος |
||
 |
[μαθηματικά] \dfrac{σι}{2} [μαθηματικά] |
[μαθηματικά] \dfrac{η}{2} [μαθηματικά] |
Centroid ενός κύκλου ή κυκλικής τομής |
||
 |
[μαθηματικά] \dfrac{ρε}{2} [μαθηματικά] |
[μαθηματικά] \dfrac{ρε}{2} [μαθηματικά] |
Centroid Εξίσωση κοίλου κυκλικού τμήματος |
||
 |
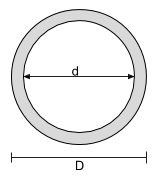[μαθηματικά] \dfrac{ρε}{2} [μαθηματικά] |
[μαθηματικά] \dfrac{ρε}{2} [μαθηματικά] |
Κεντροειδές ενός τριγώνου Isosceles |
||
 |
[μαθηματικά] \dfrac{η}{3} [μαθηματικά] |
[μαθηματικά] \dfrac{σι}{2} [μαθηματικά] |
Centroid of an I Beam |
||
 |
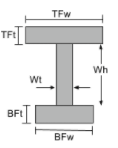[μαθηματικά] \frac{TFw φορές TFt φορές αριστερά ( BFt + Τι + \frac{TFt}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh + BFw φορές BFt} + [μαθηματικά] [μαθηματικά] \frac{Wt φορές Wh φορές αριστερά ( BFt + \frac{Τι}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh + BFw φορές BFt} + [μαθηματικά] [μαθηματικά] \frac{BFw φορές BFt φορές αριστερά ( \frac{BFt}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh + BFw φορές BFt} [μαθηματικά] |
[μαθηματικά] TFw > BFw, \frac{TFw}{2}[μαθηματικά] [μαθηματικά] BFw > TFw, \frac{BFw}{2} [μαθηματικά] |
Κεντροειδές Τ-τομής |
||
 |
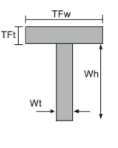[μαθηματικά] \frac{Wt φορές Wh φορές αριστερά ( \frac{Τι}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh } + [μαθηματικά] [μαθηματικά] \frac{TFw φορές TFt φορές αριστερά ( Τι + \frac{TFt}{2} \σωστά ) }{TFw φορές TFt + Wt φορές Wh } [μαθηματικά] |
[μαθηματικά] \frac{TFw}{2} [μαθηματικά] |
Κεντροειδές ενός τμήματος C |
||
 |
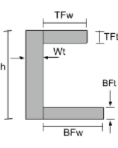[μαθηματικά] \frac{TFw φορές TFt φορές αριστερά ( η – \frac{TFt}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh + BFw φορές BFt} + [μαθηματικά] [μαθηματικά] \frac{Wt φορές h φορές αριστερά ( \frac{η}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh + BFw φορές BFt} + [μαθηματικά] [μαθηματικά] \frac{BFw φορές BFt φορές αριστερά ( \frac{BFt}{2} \σωστά )}{TFw φορές TFt + Wt φορές Wh + BFw φορές BFt} [μαθηματικά] |
[μαθηματικά] \frac{TFt φορές TFw φορές αριστερά ( Β + \frac{TFw}{2} \σωστά )}{TFt φορές TFw + h φορές Wt + BFt φορές BFw} + [μαθηματικά] [μαθηματικά] \frac{h φορές Wt φορές αριστερά ( \frac{Β}{2} \σωστά )}{TFt φορές TFw + h φορές Wt + BFt φορές BFw} + [μαθηματικά] [μαθηματικά] \frac{BFt φορές BFw φορές αριστερά ( Β + \frac{BFw}{2} \σωστά )}{TFt φορές TFw + h φορές Wt + BFt φορές BFw} [μαθηματικά] |
Κεντροειδές γωνιών |
||
 |
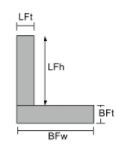[μαθηματικά] \frac{LFt φορές LFh φορές αριστερά ( BFt + \frac{LFh}{2} \σωστά ) }{LFt φορές LFh + BFw φορές BFt} + [μαθηματικά] [μαθηματικά] \frac{BFw φορές BFt φορές αριστερά ( \frac{BFt}{2} \σωστά )}{LFt φορές LFh + BFw φορές BFt} [μαθηματικά] |
[μαθηματικά] \frac{LFh φορές LFt φορές αριστερά ( \frac{LFt}{2} \σωστά )}{LFh φορές LFt + BFt φορές BFw} + [μαθηματικά] [μαθηματικά] \frac{BFt φορές BFw φορές αριστερά ( \frac{BFw}{2} \σωστά )}{LFh φορές LFt + BFt φορές BFw} [μαθηματικά] |
Automatic Equations for Centroid of Beam
Ρίξτε μια ματιά στο δικό μας Αυτό το άρθρο σάς καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid, μια απλοποιημένη έκδοση του Οικοδόμος ενότητας SkyCiv, to calculate centroid of beam automatically with no need for hand calculations. Ή εγγραφείτε σήμερα για να ξεκινήσετε!
