Πώς να υπολογίσετε μια απροσδιόριστη δέσμη – Διπλή ολοκληρωμένη μέθοδος

Ακαθόριστος δοκάρια μπορεί να είναι μια πρόκληση λόγω των επιπλέον βημάτων που απαιτούνται για την επίλυση των αντιδράσεων. Θυμηθείτε ότι οι απροσδιόριστες δομές έχουν αυτό που ονομάζεται βαθμός απροσδιόριστης. Για την επίλυση της δομής, πρέπει να εισαχθούν όρια. συνεπώς, όσο υψηλότερος είναι ο βαθμός αβεβαιότητας, πρέπει να προσδιοριστούν οι πιο οριακές συνθήκες. Αλλά πριν μπορέσουμε να λύσουμε μια απροσδιόριστη δέσμη, Πρέπει πρώτα να προσδιορίσουμε εάν η δέσμη είναι στατικά απροσδιόριστη. Καθώς οι δοκοί είναι μονοδιάστατες κατασκευές, Η χρήση της εξίσωσης για τον προσδιορισμό εξωτερικά στατικά απροσδιόριστων δομών είναι αρκετή.

[μαθηματικά]
Εγώ_{μι}= R- αριστερά ( 3+μι_{ντο} \σωστά )
[μαθηματικά]

Οπου:

• Εγώ_μι = Βαθμός αβεβαιότητας
• R = Συνολικός αριθμός αντιδράσεων
• μι_ντο = Εξωτερικές συνθήκες (π.χ. εσωτερική άρθρωση)

Τυπικά, ωστόσο, χωρίς να χρειάζεται επίλυση για τον βαθμό απροσδιοριστίας, οτιδήποτε άλλο εκτός από απλές εκτάσεις ή δοκούς προβόλου είναι στατικά απροσδιόριστος, υποθέτοντας ότι τέτοιες δοκοί δεν έρχονται με εσωτερικούς μεντεσέδες.

Υπάρχουν πολλοί τρόποι προσέγγισης για την επίλυση απροσδιόριστων δοκών. Αν και για λόγους απλότητας και ομοιότητας με το SkyCiv Beam υπολογισμοί χεριών, θα συζητήσουμε τη μέθοδο διπλής ολοκλήρωσης.

Διπλή ολοκλήρωση

Η Διπλή Ενσωμάτωση είναι ίσως η απλούστερη όλων των μεθόδων για την ανάλυση των δοκών. Η ιδέα για αυτή τη μέθοδο είναι αρκετά απλή σε αντίθεση με άλλες μεθόδους, καθώς βασίζεται κυρίως σε μια βασική κατανόηση του ολοκληρωτικού λογισμού, εξ ου και το όνομα. Ένα κομμάτι ακέραιου λογισμού προσαρμόζεται από τη σχέση της καμπυλότητας της δέσμης με τη στιγμή που φαίνεται παρακάτω.

[μαθηματικά]
\frac{1}{\Ρο}= frac{Μ}{ΟΧΙ}
[μαθηματικά]

Σημειώστε ότι το 1 / ρ είναι η καμπυλότητα της δέσμης και ότι το ρ είναι η ακτίνα της καμπύλης. Βασικά, Ο ορισμός της καμπυλότητας είναι ο ρυθμός αλλαγής της εφαπτομένης σε σχέση με το μήκος του τόξου. Καθώς η στιγμή είναι συνάρτηση της φόρτωσης σε σχέση με το μήκος του μέλους, Η ενσωμάτωση της καμπυλότητας σε σχέση με το μήκος του μέλους θα δώσει την κλίση της δοκού. Ομοίως, Η ενσωμάτωση της κλίσης σε σχέση με το μήκος του μέλους θα δώσει την εκτροπή της δέσμης. Ως τυπικά δομικά φορτία έχουν αλγεβρική φύση, Η ενσωμάτωση αυτών των εκφράσεων είναι τόσο απλή όσο η χρήση του γενικού τύπου ισχύος.

[μαθηματικά]
\int f αριστερά ( x δεξιά )^{ν}dx = frac{f αριστερά ( x δεξιά )^{n + 1}}{n + 1}+ντο
[μαθηματικά]

Ίσως ο καλύτερος τρόπος για να κατανοήσετε την έννοια είναι να δώσετε ένα παράδειγμα δέσμης με τα ακόλουθα.

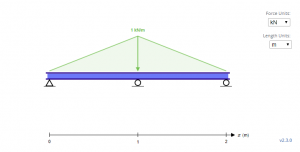
Η παραπάνω δέσμη δείγματος είναι μια απροσδιόριστη δέσμη με τριγωνικά φορτία. Με την υποστηρίζει, ΕΝΑ_και, σι_και και Γ_και για τον πρώτο, δεύτερος, και τρίτη υποστήριξη αντίστοιχα, το πρώτο βήμα για την επίλυση αυτών των άγνωστων είναι ξεκινώντας με τις εξισώσεις ισορροπίας.

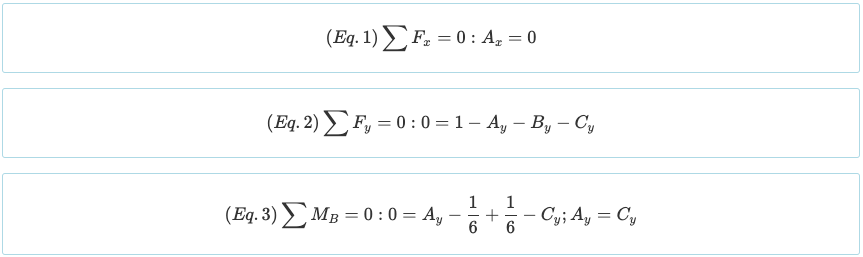
Σημειώστε ότι η δοκός έχει βαθμό στατική αβεβαιότητα από 1°. Καθώς υπάρχουν τέσσερα άγνωστα (ΕΝΑ_Χ, ΕΝΑ_και, σι_και, και Γ_και) και υπάρχουν μέχρι τώρα τρεις εξισώσεις από τις παραπάνω εξισώσεις ισορροπίας, Είναι απαραίτητο να δημιουργηθεί μια ακόμη εξίσωση από τις οριακές συνθήκες. Θυμηθείτε ότι η ροπή που δημιουργείται από ένα σημειακό φορτίο και ένα τριγωνικό φορτίο είναι τα ακόλουθα.

Σημείο φόρτωσης:

[μαθηματικά]
Μ = F φορές x; Μ = Fx
[μαθηματικά]

Τριγωνικό φορτίο:

[μαθηματικά]
Μ = frac{w_{0}\φορές x}{2}\φορές αριστερά ( \frac{Χ}{3} \σωστά ); Μ = frac{w_{0}x ^{2}}{6}
[μαθηματικά]

Χρησιμοποιώντας τη μέθοδο διπλής ολοκλήρωσης, Αυτές οι νέες εξισώσεις γίνονται και εμφανίζονται παρακάτω.

Σημείωση: Οι παραπάνω εξισώσεις γράφονται ως λειτουργίες Macaulay όπου μια έκφραση ισούται με μηδέν όταν Χ < μεγάλο. Σε αυτήν την περίπτωση, L = 1.

Στις παραπάνω εξισώσεις, παρατηρήστε ότι ο τέταρτος όρος που προστέθηκε φαίνεται να βγαίνει από το πουθενά. στην πραγματικότητα, η διεύθυνση της φόρτωσης είναι αντίθετη από την κατεύθυνση της βαρύτητας. Αυτό οφείλεται στο γεγονός ότι οι εξισώσεις για τριγωνικά φορτία λειτουργούν μόνο όταν το φορτίο αυξάνεται καθώς αυξάνεται το μήκος. Αυτό δεν είναι πολύ ένα θέμα για εξισώσεις για διανέμονται και φορτία σημείου λόγω της συμμετρίας τους. Σε ισχύ, η ισοδύναμη φόρτωση για τη δοκό παραπάνω μοιάζει με τη δοκό παρακάτω, έτσι οι εξισώσεις βασίζονται σε αυτήν.

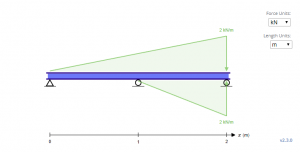
Για επίλυση για C₁ και Γ₂, πρέπει να καθοριστούν οι οριακές συνθήκες. Στην παραπάνω δέσμη, μπορεί να παρατηρηθεί ότι υπάρχουν τρεις τέτοιες οριακές συνθήκες Χ = 0, Χ = 1, και Χ = 2, όπου η παραμόρφωση y είναι μηδενική στις τρεις θέσεις.

Όριο ορίου 1

[μαθηματικά]
x = 0, y = 0; ΝΤΟ_{2}= 0
[μαθηματικά]

Όριο ορίου 2

[μαθηματικά]
x = 0, y = 0; ΝΤΟ_{1}= frac{1}{120}-\frac{ΕΝΑ_{και}}{6}
[μαθηματικά]

Μετά τον προσδιορισμό των τιμών κάθε σταθεράς, Η τελευταία εξίσωση μπορεί τώρα να ληφθεί χρησιμοποιώντας την τελευταία συνθήκη ορίου.

Όριο ορίου 3

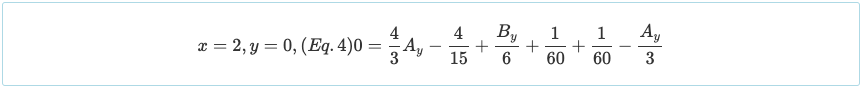
Σημειώστε ότι η οριακή συνθήκη του θ = 0 στο x = 1 μπορεί να χρησιμοποιηθεί, αν και ισχύει μόνο για τη μεσαία αντίδραση μιας συμμετρικής συνεχούς δέσμης με συμμετρική φόρτιση.

Καθώς έχουν καθοριστεί οι τέσσερις εξισώσεις, μπορούν τώρα να λυθούν ταυτόχρονα. Η επίλυση αυτών των εξισώσεων θα δώσει τις ακόλουθες αντιδράσεις.

Με τις αντιδράσεις καθορισμένες, οι τιμές των αντιδράσεων μπορούν να αντικατασταθούν από την εξίσωση στιγμής. Αυτό θα μας επιτρέψει να προσδιορίσουμε την τιμή της ροπής σε οποιοδήποτε μέρος του συστήματος δέσμης.

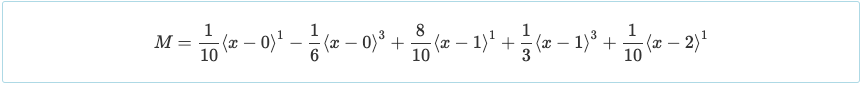
Μια άλλη ευκολία της Διπλής Ολοκλήρωσης είναι ότι η εξίσωση στιγμής παρουσιάζεται με τρόπο που μπορεί να χρησιμοποιηθεί για την επίλυση της διάτμησης με τη σχέση που φαίνεται παρακάτω.

[μαθηματικά]
V = frac{dM}{dx}
[μαθηματικά]

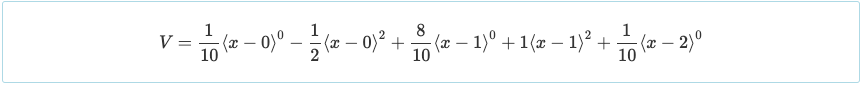
Πάλι, χρησιμοποιώντας μόνο μια βασική κατανόηση του διαφορικού λογισμού, Η εξίσωση του παραγώγου μιας συνάρτησης στο μηδέν αποδίδει το μέγιστο ή το ελάχιστο αυτής της συνάρτησης. Ετσι, εξίσωση V = 0 θα οδηγήσει σε μια μέγιστη θετική στιγμή στις Χ = 0.447 και Χ = 1.553 του Μ = 0.030

Φυσικά, Όλα αυτά μπορούν να επαληθευτούν με το SkyCiv Beam.

Λογισμικό SkyCiv Beam

Λογισμικό ανάλυσης δέσμης SkyCiv επιτρέπει στους χρήστες να αναλύουν τις δομές δοκών εύκολα και με ακρίβεια. Μπορείτε να λάβετε μια ανάλυση του μέλους δοκού σας, συμπεριλαμβανομένου αντιδράσεις, δύναμη διάτμησης, στιγμή κάμψης, εκτροπή, και στρες μέσα σε λίγα δευτερόλεπτα.

Αν θέλετε να το δοκιμάσετε πρώτα, Υπολογιστής δωρεάν δέσμης είναι ένας πολύ καλός τρόπος για να ξεκινήσετε, ή απλά εγγραφείτε δωρεάν σήμερα!