Ένας οδηγός για τον Στατικό Προσδιορισμό, Απροσδιοριστία, και Αστάθεια

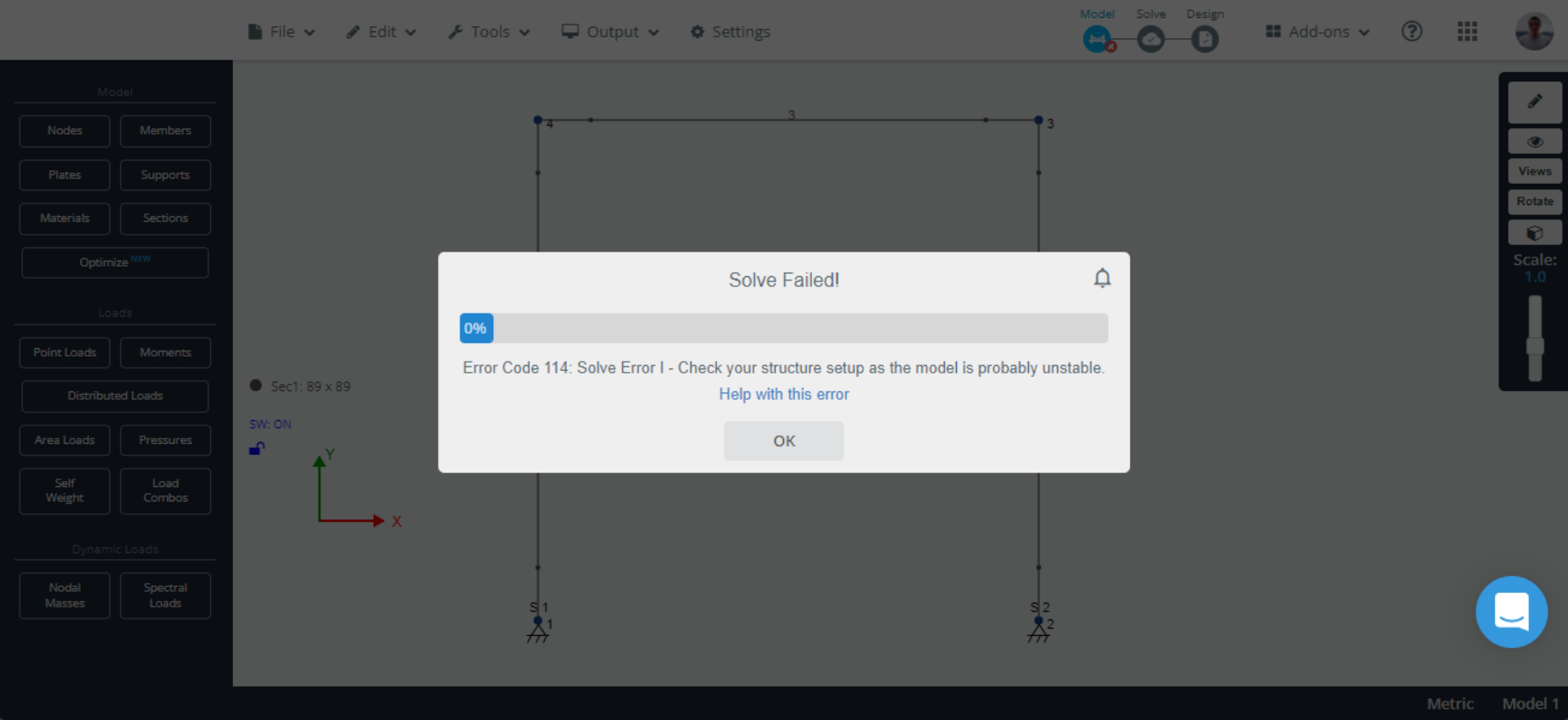
Αφού μοντελοποιηθεί πλήρως η κατασκευή και εφαρμοστούν τα φορτία, είναι καιρός να λύσουμε το σύστημα για να βρούμε όλα τα αποτελέσματα που προέρχονται από το στάδιο της ανάλυσης: αντιδράσεις, εσωτερικές δυνάμεις (δύναμη διάτμησης, στιγμή κάμψης, αξονική δύναμη, και στρέψη), μετατοπίσεις, και τονίζει. Μερικές φορές τα πράγματα δεν πάνε όπως αναμενόταν και όταν πρόκειται για επίλυση, μπορεί να λάβετε ένα ενοχλητικό μήνυμα που λέει “Η επίλυση απέτυχε! Ελέγξτε τη ρύθμιση της δομής σας, καθώς το μοντέλο είναι μάλλον ασταθές”, και οι πιθανότητες είναι ότι δεν ξέρετε ακριβώς τι είναι λάθος με το μοντέλο. Αυτό το άρθρο εξηγεί την έννοια της δομικής σταθερότητας μαζί με τον στατικό προσδιορισμό και την απροσδιοριστία που είναι πολύ σχετικά θέματα, Παρουσιάζει επίσης μερικές συμβουλές για την αντιμετώπιση προβλημάτων ενός ασταθούς μοντέλου.

Γενικά, μια κατασκευή θεωρείται εσωτερικά σταθερή εάν διατηρεί το σχήμα της όταν αφαιρούνται τα στηρίγματα. Αντίστροφως, μια κατασκευή θεωρείται εσωτερικά ασταθής εάν μόλις αποκολληθεί από τα στηρίγματα, η κατασκευή δεν μπορεί να διατηρήσει το σχήμα της και μπορεί να υποστεί μεγάλες μετατοπίσεις ή ακόμα και να καταρρεύσει. Εχοντας πεί αυτό, θα ρίξουμε μια πιο προσεκτική ματιά στον τύπο στατικού προσδιορισμού, τόσο για εσωτερικά ασταθείς όσο και για σταθερές κατασκευές. Ο τύπος στατικού προσδιορισμού βοηθά στην ταξινόμηση μιας δομής ως εξωτερικά ασταθούς, στατικά καθορισμένο, ή στατικά απροσδιόριστο.

Στατικός προσδιορισμός εσωτερικά σταθερών κατασκευών

Μια εσωτερικά σταθερή δομή μπορεί να ληφθεί ως εξωτερικά προσδιοριζόμενη στατικά εάν όλες οι αντιδράσεις υποστήριξής της μπορούν να λυθούν με την επίλυση των εξισώσεων ισορροπίας. Για επίπεδες κατασκευές υπό επίπεδα φορτία, χρειάζεται να υπάρχουν τρεις υποστηρικτικές αντιδράσεις για να είναι η δομή σε ισορροπία. Επιπροσθέτως, αφού υπάρχουν μόνο τρεις διαθέσιμες εξισώσεις ισορροπίας, τρεις αντιδράσεις μπορούν να βρεθούν το πολύ, οπότε θα πρέπει να υπάρχουν ακριβώς τρεις αντιδράσεις που υποστηρίζουν την επίπεδη δομή. Μερικά παραδείγματα εξωτερικά στατικά καθορισμένων επίπεδων δομών φαίνονται στην παρακάτω εικόνα:

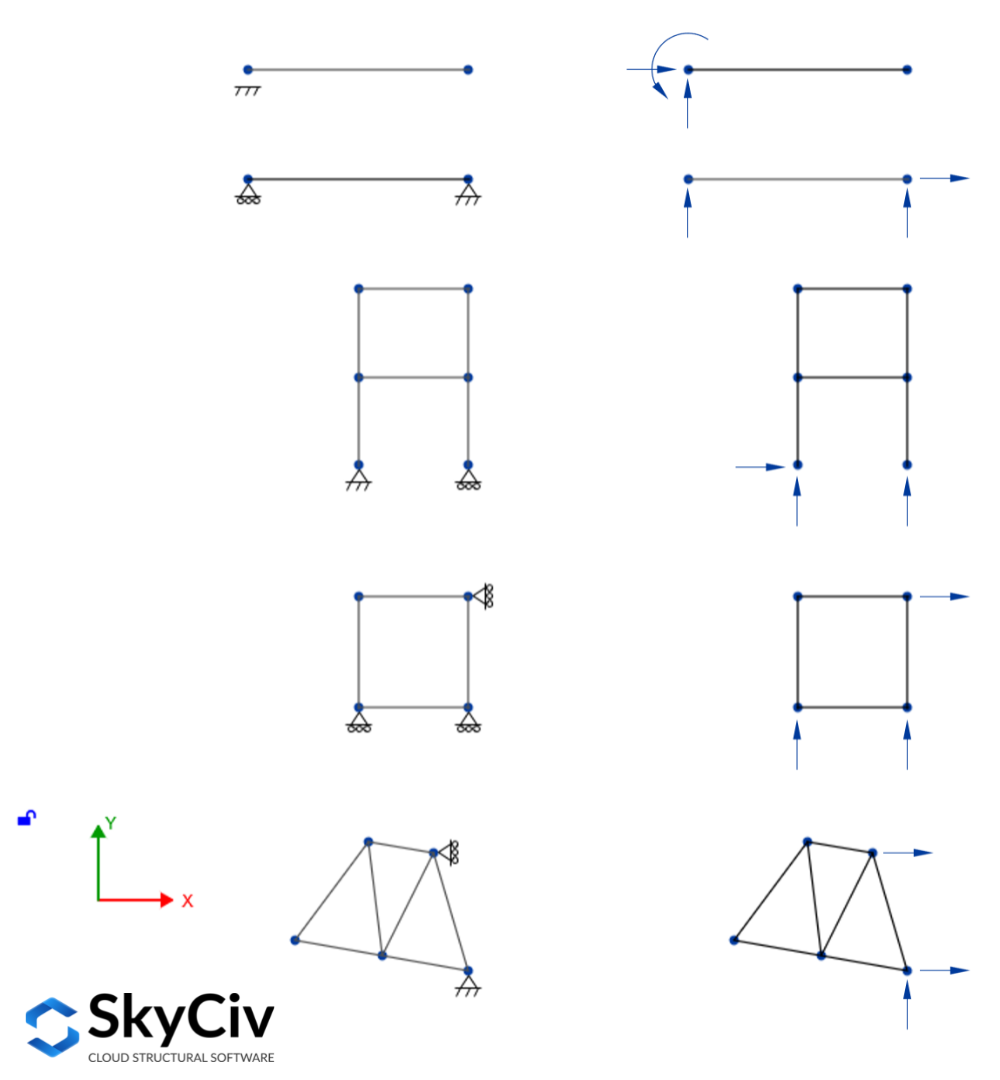
Όταν περισσότερες από τρεις αντιδράσεις υποστηρίζουν τη δομή, ονομάζεται στατικά ακαθόριστη εξωτερικά δομή, αφού δεν είναι δυνατό να λυθούν όλες οι αντιδράσεις χρησιμοποιώντας τις τρεις εξισώσεις ισορροπίας. Αυτές οι αντιδράσεις ονομάζονται εξωτερικές περιττές και ο αριθμός των εξωτερικών περιττών είναι γνωστός ως βαθμός εξωτερικής απροσδιοριστίας, γραμμένο ως εξίσωση μοιάζει με αυτό:

\(i_e = r – 3\)

Οπου \(r) είναι ο αριθμός των αντιδράσεων που υποστηρίζουν τη δομή.

Στις περιπτώσεις που η κατασκευή υποστηρίζεται από λιγότερες από τρεις αντιδράσεις στήριξης, αυτά δεν αρκούν για να αποτρέψουν τη μετακίνηση της δομής στο επίπεδό της, δεδομένου ότι αυτή η δομή δεν θα παραμείνει σε ισορροπία κάτω από ένα γενικό σύστημα φορτίων, ονομάζεται στατικά ασταθής εξωτερικά. Με βάση τον αριθμό των αντιδράσεων \(r), είναι δυνατόν να προσδιοριστεί ο στατικός προσδιορισμός, αβεβαιότητα, και αστάθεια εσωτερικά σταθερών δομών με βάση τα κριτήρια που ακολουθούν:

\( r αρχή{θα θεωρήσουμε το επίγειο ηλιακό πάνελ ως ένα ανοιχτό μονόκλιτο κτίριο όταν η γωνία κλίσης είναι μικρότερη ή ίση με 45° και ως σταθερό σημάδι για γωνία κλίσης μεγαλύτερη από 45°} < 3, \; \textrm{στατικά ασταθής εξωτερικά δομή} \\ = 3, \; \textrm{προσδιορίζουν στατικά εξωτερικά τη δομή} \\ > 3, \; \textrm{στατικά απροσδιόριστη εξωτερικά δομή} \τέλος{θα θεωρήσουμε το επίγειο ηλιακό πάνελ ως ένα ανοιχτό μονόκλιτο κτίριο όταν η γωνία κλίσης είναι μικρότερη ή ίση με 45° και ως σταθερό σημάδι για γωνία κλίσης μεγαλύτερη από 45°}\)

Είναι σημαντικό να αναφέρουμε ότι εφόσον πληρούνται οι δύο τελευταίες προϋποθέσεις, δεν είναι σίγουρο ότι η δομή θα είναι σταθερή. Σημαίνει ότι ακόμη και όταν η δομή υποστηρίζεται από περισσότερες από τρεις αντιδράσεις, εάν στηρίξει και δεν είναι σωστά διατεταγμένη, η δομή μπορεί να εξακολουθεί να είναι ασταθής. Αυτό ονομάζεται γεωμετρική εξωτερική αστάθεια και προκαλείται από δύο βασικούς λόγους:

• Όταν όλες οι αντιδράσεις’ οι γραμμές δράσης είναι παράλληλες επειδή η δομή δεν θα εμποδίζεται να μετατοπιστεί στην κάθετη κατεύθυνση των αντιδράσεων
• Όταν όλες οι αντιδράσεις’ οι γραμμές δράσης είναι ταυτόχρονες σε ένα σημείο επειδή η δομή θα επιτρέπεται να περιστρέφεται γύρω από το σημείο ταυτόχρονης

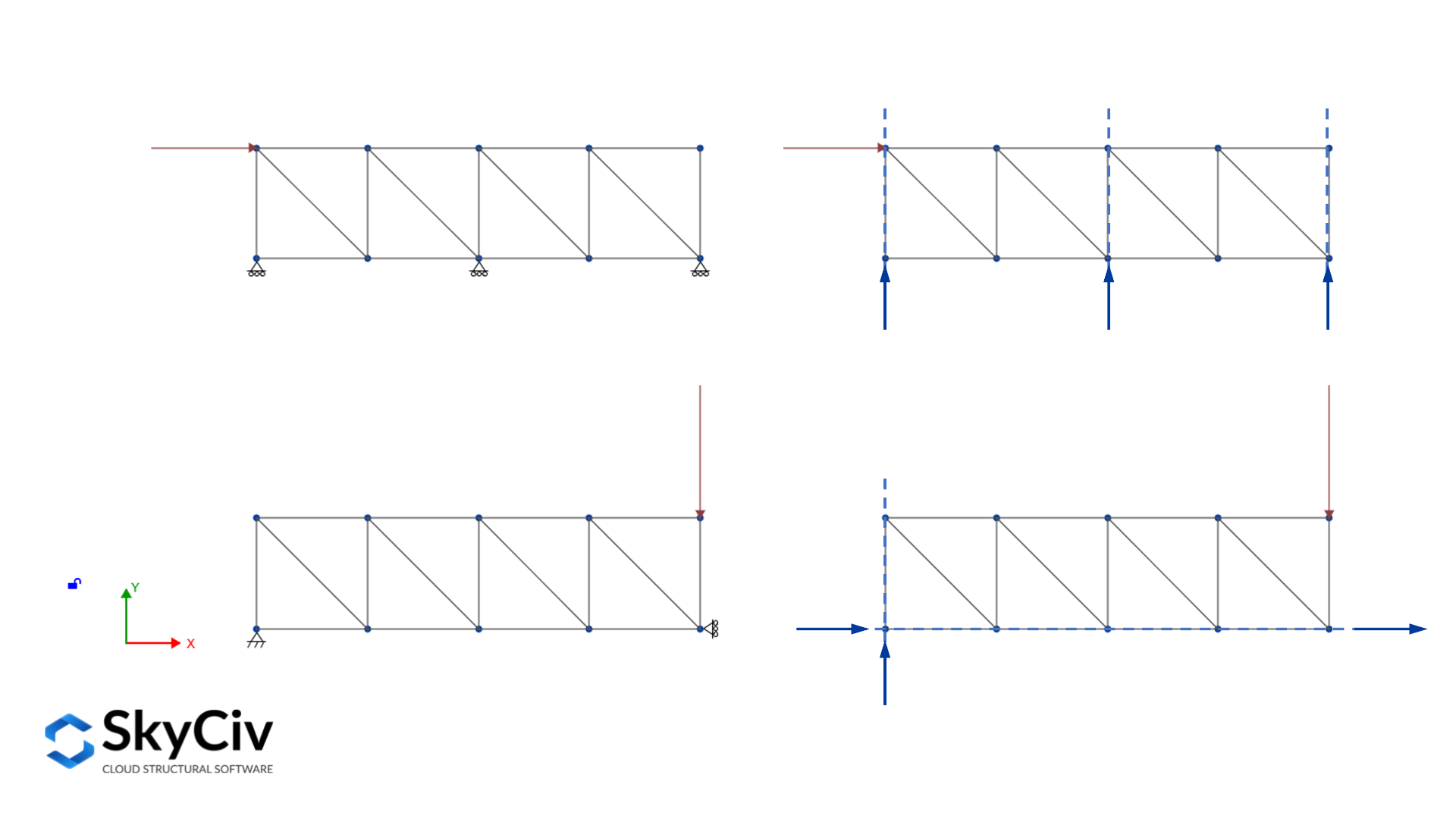
Στατικός προσδιορισμός εσωτερικά ασταθών δομών

Εσωτερικά ασταθείς κατασκευές είναι εκείνες που όταν αποσπαστούν από τα στηρίγματα δεν μπορούν να κρατήσουν το αρχικό τους σχήμα. Χωρίς στηρίγματα, τα μέλη της κατασκευής θα υφίσταντο μεγάλες μετατοπίσεις μεταξύ τους. Για να ορίσετε τον στατικό προσδιορισμό, αβεβαιότητα, και εξωτερική σταθερότητα αυτών των δομών, οι εξισώσεις αλλάζουν λόγω των πρόσθετων εξισώσεων συνθήκης που μπαίνουν στο παιχνίδι λαμβάνοντας υπόψη τις ειδικές συνδέσεις μεταξύ των μελών. Οι ειδικές συνδέσεις είναι αυτές που δεν μεταδίδουν στιγμή, δύναμη διάτμησης, ή αξονική δύναμη.

Ως παράδειγμα, εξετάστε τη δομή στην παρακάτω εικόνα (πάνω τμήμα), υποστηρίζεται ξεκάθαρα από τρεις αντιδράσεις, αλλά αυτά δεν αρκούν για να εξασφαλιστεί η ισορροπία υπό τις ασκούμενες δυνάμεις εντός του επιπέδου χάρη στην παρουσία της άρθρωσης μεταξύ των μελών, χρειάζεται τέταρτο μη παράλληλο, μη ταυτόχρονη αντίδραση για να εξασφαλιστεί η ισορροπία (κάτω τμήμα).

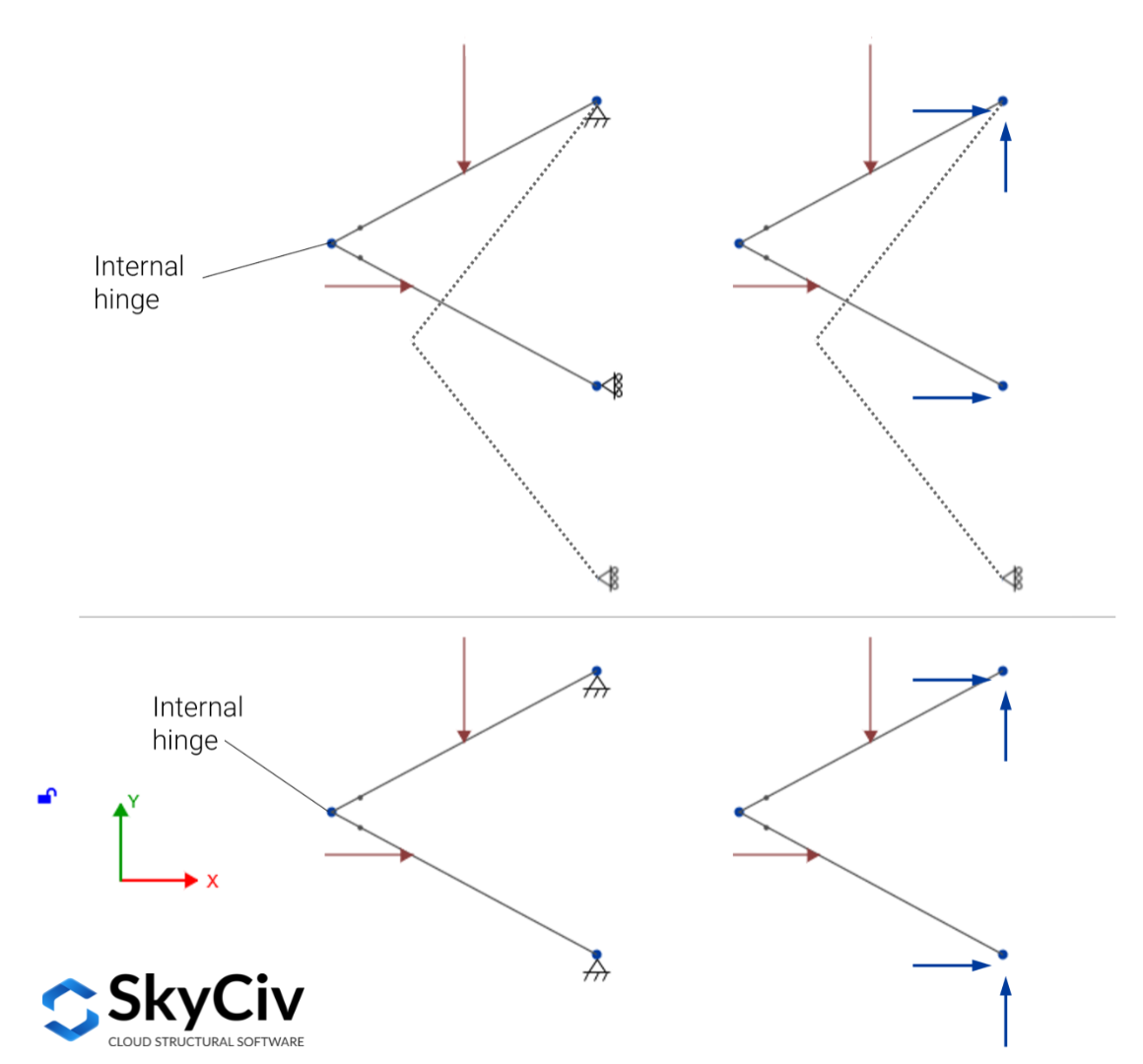
Γενικά, για εσωτερικά ασταθείς κατασκευές, με βάση τον αριθμό των αντιδράσεων \(r) και εξισώσεις συνθήκης \(e_c), είναι δυνατόν να προσδιοριστεί ο στατικός προσδιορισμός, αβεβαιότητα, και αστάθεια εσωτερικά σταθερών δομών με βάση τα κριτήρια που ακολουθούν:

\( r αρχή{θα θεωρήσουμε το επίγειο ηλιακό πάνελ ως ένα ανοιχτό μονόκλιτο κτίριο όταν η γωνία κλίσης είναι μικρότερη ή ίση με 45° και ως σταθερό σημάδι για γωνία κλίσης μεγαλύτερη από 45°} < 3 + e_c, \; \textrm{στατικά ασταθής εξωτερικά δομή} \\ = 3 + e_c, \; \textrm{προσδιορίζουν στατικά εξωτερικά τη δομή} \\ > 3 + e_c, \; \textrm{στατικά απροσδιόριστη εξωτερικά δομή} \τέλος{θα θεωρήσουμε το επίγειο ηλιακό πάνελ ως ένα ανοιχτό μονόκλιτο κτίριο όταν η γωνία κλίσης είναι μικρότερη ή ίση με 45° και ως σταθερό σημάδι για γωνία κλίσης μεγαλύτερη από 45°}\)

Για απροσδιόριστες εξωτερικά εσωτερικά ασταθείς δομές, ο βαθμός της εξωτερικής απροσδιοριστίας μπορεί να εκφραστεί ως εξής:

\(i_e = r – (3 + e_c)\)

Σύνοψη

Για επίπεδες κατασκευές που είναι εσωτερικά σταθερές να είναι εξωτερικά σταθερές, που σημαίνει ότι παραμένει σε ισορροπία κάτω από ένα γενικό σύστημα φορτίων, πρέπει να ισχύουν τα παρακάτω:

• Η δομή υποστηρίζεται από τρεις ή περισσότερες αντιδράσεις
• Όλες οι αντιδράσεις δεν μπορούν να είναι παράλληλες ή ταυτόχρονες

Για επίπεδες κατασκευές που είναι εσωτερικά ασταθείς να είναι εξωτερικά σταθερές, που σημαίνει ότι παραμένει σε ισορροπία κάτω από ένα γενικό σύστημα φορτίων, πρέπει να ισχύουν τα παρακάτω:

• Ο αριθμός των αντιδράσεων που υποστηρίζουν τη δομή είναι μεγαλύτερος ή ίσος με τον αριθμό των εξισώσεων της συνθήκης συν τρεις
• Όλες οι αντιδράσεις δεν μπορούν να είναι παράλληλες ή ταυτόχρονες

Αντιμετώπιση προβλημάτων ασταθούς δομής στο S3D

Υπάρχουν μερικά πράγματα που μπορείτε να δοκιμάσετε όταν το μοντέλο δεν λύνεται, και παίρνετε το “Ασταθής δομή” μήνυμα σφάλματος:

• Επιλέξτε όλα τα μέλη και βεβαιωθείτε ότι έχουν τις επισκευές τους ως προς το τέλος των μελών τους “FFFFFF”, και προσπαθήστε να εκτελέσετε το μοντέλο. Εάν ορισμένα μέλη πρέπει να έχουν διαφορετική σταθερότητα στο τελικό μοντέλο, ξεκινήστε να το αλλάζετε ένα προς ένα και λύστε τη δομή για να δείτε ποιο είναι το ακριβές μέλος ή το σύνολο μελών που προκαλεί την αστάθεια.
• Επιλέξτε όλα τα μέλη και αλλάξτε τον τύπο τους από κανονικό σε συνεχές, που θα συνέδεε σωστά μέλη που δεν έχουν κόμβο στη διασταύρωση αλλά προορίζονται να συνδεθούν.
• Καταργήστε από την ανάλυση όλα τα καλώδια, και προσπαθήστε να λύσετε το μοντέλο. Για να μάθετε πώς να καταπιέζετε τα μέλη, Συνδέσεις/Υποστήριξη αυτό το άρθρο.

βιβλιογραφικές αναφορές

Κασιμάλη, Aslam. «3.4 Στατικός Προσδιορισμός, Απροσδιοριστία, και αστάθεια». Δομική ανάλυση, Cengage Learning, 2011.