ΟΡΘΟΤΡΟΠΙΚΑ ΥΛΙΚΑ
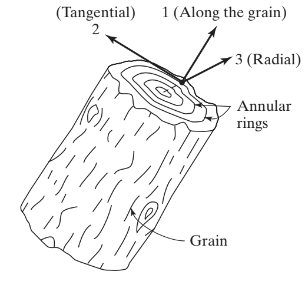
Πριν περάσετε από μια εξήγηση των ορθοτροπικών πλακών, Ας δούμε μερικά παραδείγματα ορθότροπων υλικών. Υλικά όπως κρύσταλλοι τοπάζι και βαρίτης είναι ορθότροπα (Τσαντροπάτλα, 2012). Ένα άλλο πολύ διαδεδομένο ορθοτροπικό υλικό είναι το ξύλο. Φιγούρα 1 δείχνει τους κύριους άξονες στους οποίους ορίζονται οι μηχανικές ιδιότητες για το ξύλο.
Φιγούρα 1. Το ξύλο ως ορθότροπο υλικό (Τσαντροπάτλα & Belegundu ,2012, σελίδα 233)
Αξονας 1 ορίζεται κατά μήκος του κόκκου ή των ινών; άξονας 2 είναι εφαπτομενική και άξονας 3 τρέχει ακτινωτά. Ο γενικευμένος νόμος του Hooke για αυτό το παράδειγμα (και για οποιοδήποτε άλλο ορθοτροπικό υλικό) μπορεί να γραφτεί ως
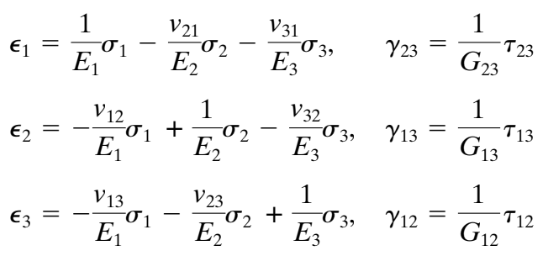
Εξισώσεις 1. Γενικευμένος Νόμος του Χουκ (Τσαντροπάτλα & Belegundu,2012, σελίδα 233)
Οπου:
- ε1, ε2, ε3 είναι τα φυσιολογικά στελέχη.
- γ12, γ13, γ23 είναι οι διατμητικές παραμορφώσεις.
- μι1, μι2, και Ε3 είναι το μέτρο του Young κατά μήκος του κύριου άξονα.
- σολ12, σολ13, σολ23 είναι το μέτρο διάτμησης.
- ν21, ν31, ν12, ν32, ν23 είναι οι αναλογίες του Poisson.
- Για συνδυασμένους δείκτες, Ο πρώτος αριθμός δείχνει πού ασκείται τάση και ο δεύτερος όπου συμβαίνει παραμόρφωση.
Επομένως, Η κύρια διαφορά σε ένα ορθότροπο υλικό είναι ότι έχουμε διαφορετικές μηχανικές ιδιότητες κατά μήκος των κύριων αξόνων, αυτό είναι, “Χ”, “και”, “με”.
ΟΡΘΟΤΡΟΠΙΚΑ ΠΛΑΚΑ
Υπάρχουν μερικές συνήθεις περιπτώσεις χρήσης για πλάκες στη δομική μηχανική, που μπορούμε να συνοψίσουμε ως εξής: ισοτροπικό επίπεδο, σύνθετο ή σάντουιτς και σκληρυμένο (Οι W. Jiang et al, 1997).
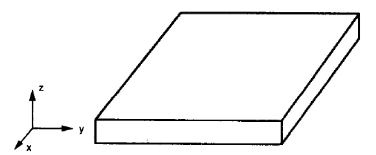
Οι ισοτροπικές επίπεδες πλάκες είναι κανονικές πλάκες (σχήμα αρ.2), χρειάζεται μόνο για να οριστεί μια τιμή για την αναλογία Poisson, Νέος, και μέτρο διάτμησης γιατί οι μηχανικές ιδιότητες σε καμία κατεύθυνση δεν αλλάζουν.
Εικόνα αρ.2. Οι επίπεδες πλάκες είναι συνήθως ισότροπες (Οι W. Jiang et al, 1997, σελίδα 106)
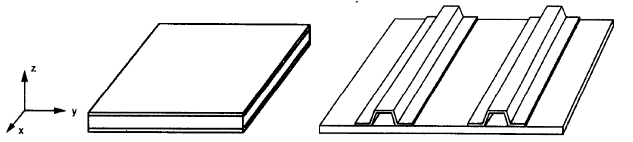
Για τις δύο τελευταίες επιλογές, σάντουιτς και σκληρυμένα πιάτα (σχήμα αρ.3), πρέπει να ορίσουμε διαφορετικές μηχανικές ιδιότητες στον κύριο άξονά τους. Αυτές οι διαφορετικές τιμές κάνουν τις πλάκες ορθοτροπικές.
Φιγούρα 3. Σύνθετος (αριστερά) και πλάκες ενισχυμένες με καπέλο (σωστά) (Οι W. Jiang et al, 1997, σελίδα 106)
Σε ορθοτροπικό πιάτο, θα είχαμε δύο άξονες με την ίδια ακαμψία, σχήμα αρ.3. Οι άξονες "x" και "y" βρίσκονται σε ένα επίπεδο, και το "z" είναι κάθετο σε αυτό.
Μπορούμε να το πούμε αυτό (Οι W. Jiang et al, 1997):
- μιΧ = μικαι ≠ μιμε ; (μιΧ, μικαι )> μιμε .
- νxz = νyz ≠ νxy ; (νxz, νyz) >νxy
- σολxy = σολxz = σολyz
Οι εκφράσεις που υποδεικνύονται προηγουμένως υποδηλώνουν ότι η ακαμψία στις κατευθύνσεις "x" και "y" είναι υψηλότερη από το "z". Οι λόγοι του Poisson δείχνουν επίσης ότι υπάρχει μεγαλύτερη παραμόρφωση σε επίπεδα που σχετίζονται με την κατεύθυνση "z" παρά σε επίπεδο που σχηματίζεται από τους άξονες "x" και "y"..
ΠΑΡΑΔΕΙΓΜΑ
Περιγραφή και Ρύθμιση
Να συνοψίσει τις έννοιες που μάθαμε σε προηγούμενες ενότητες, πρόκειται να αναπτύξουμε ένα παράδειγμα στο SkyCiv. Αποτελείται από την ανάλυση ενός πάνελ τοίχου/πλάκας σάντουιτς που είναι κατασκευασμένο με δύο στρώματα εκτοξευόμενου σκυροδέματος που χωρίζονται από έναν πυρήνα πολυστυρενίου. Επιλέξαμε την επόμενη αναφορά για τις μηχανικές ιδιότητες που θα χρησιμοποιηθούν στη μοντελοποίηση: Οι Torres Villavicencio et al. (2013).

Φιγούρα 4. Πάνελ τοίχου/πλάκας σάντουιτς
Για να καταγράψουμε τη διαφορά ανάλυσης σε πλάκες όταν επιλέγουμε τις προηγμένες επιλογές (ορθοτροπικό), αναπτύσσουμε μια σύντομη σύγκριση του σάντουιτς πάνελ που περιγράφεται παραπάνω και μια προσέγγιση στις μηχανικές τους ιδιότητες χρησιμοποιώντας μια ισοτροπική προσέγγιση. Η τελευταία περίπτωση χρησιμοποιεί τιμές στις μηχανικές ιδιότητες που δεν αλλάζουν κατά μήκος των κύριων αξόνων τους.
Ο στόχος αυτού του παραδείγματος είναι η σύγκριση των αποτελεσμάτων ως προς την κατακόρυφη μετατόπιση. Η ρύθμιση του μοντέλου φαίνεται στο σχήμα 5.
 Φιγούρα 5. Ρύθμιση μοντέλου. Ορθότροπος (αριστερά), Ισότροπος (σωστά)
Φιγούρα 5. Ρύθμιση μοντέλου. Ορθότροπος (αριστερά), Ισότροπος (σωστά)
Μηχανικές ιδιότητες
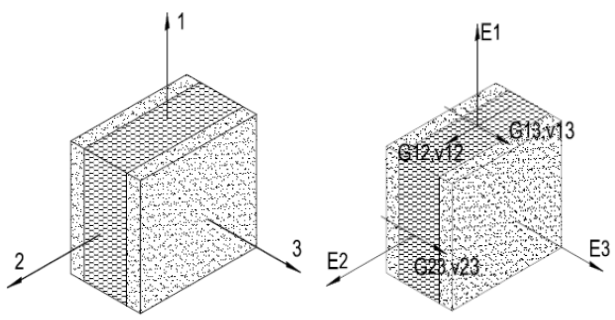
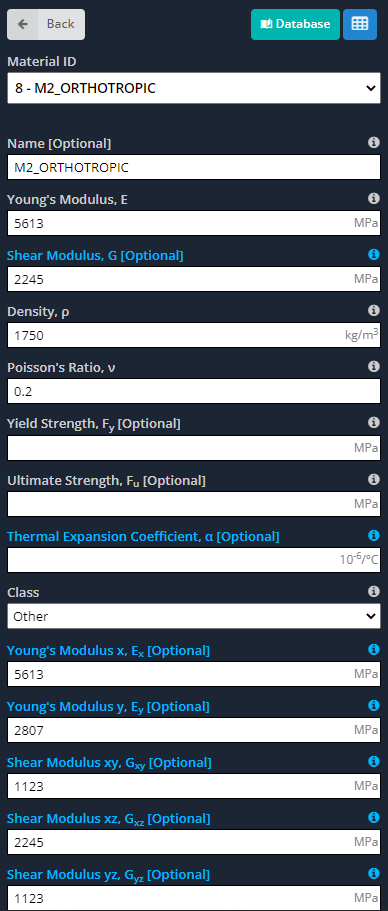
Με βάση διαφορετικές εκθέσεις εργαστηριακών δοκιμών, οι ορθοτροπικές ιδιότητες του πάνελ είναι (Οι Torres Villavicencio et al, 2013):
| Ιδιοκτησία | αξία |
|---|---|
| μι1 (MPa) | 5613 |
| μι2 (MPa) | 5613 |
| μι3 (MPa) | 2807 |
| σολ12 (MPa) | 2245 |
| σολ23 (MPa) | 1123 |
| σολ13 (MPa) | 1123 |
| ν12 | 0.2 |
| ν23 | 0.25 |
| ν13 | 0.25 |
Πίνακας αρ.1. Ορθοτροπικές Μηχανικές Ιδιότητες Πάνελ Σάντουιτς
Εικόνα αρ.6. Κύριοι άξονες στο στοιχείο του πίνακα (Οι Torres Villavicencio et al, 2013).
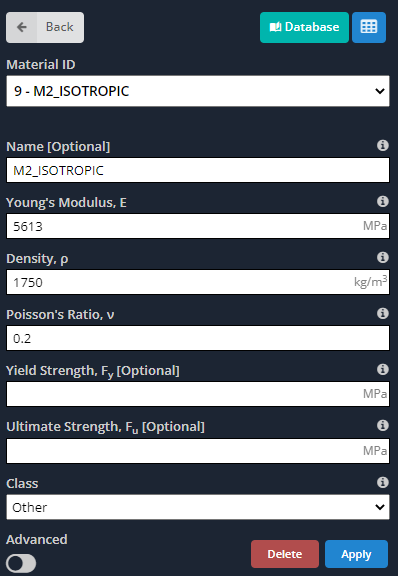
Η προσέγγιση για την ισότροπη περίπτωση υποδεικνύεται στον παρακάτω πίνακα.
| Ιδιοκτησία | αξία |
|---|---|
| μι (MPa) | 5613 |
| σολ (MPa) | 2245 |
| ν | 0.20 |
Πίνακας αρ.2. Προσέγγιση ισοτροπικών μηχανικών ιδιοτήτων πάνελ σάντουιτς
Μοντελοποίηση στο SkyCiv
Τώρα περιγράφουμε με πολύ συνοπτικό τρόπο τα βήματα που απαιτούνται για τη μοντελοποίηση του παραδείγματος. (Για περισσότερες λεπτομέρειες στη μοντελοποίηση πιάτων, συμβουλευτείτε αυτόν τον σύνδεσμο Μοντελοποίηση πλακών SkyCiv). Δεν έχω δοκιμάσει το SkyCiv, ακολουθήστε χρησιμοποιώντας το Structural 3D, απλά εγγραφείτε δωρεάν εδώ.
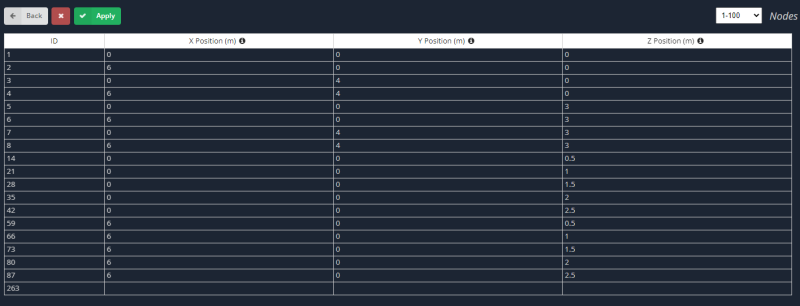
- Κόμβοι: Να δημιουργηθούν και οι δύο περιπτώσεις, ορίζουμε πρώτα τους κόμβους που αντιστοιχούν στην οριζόντια και κάθετη πλάκα.

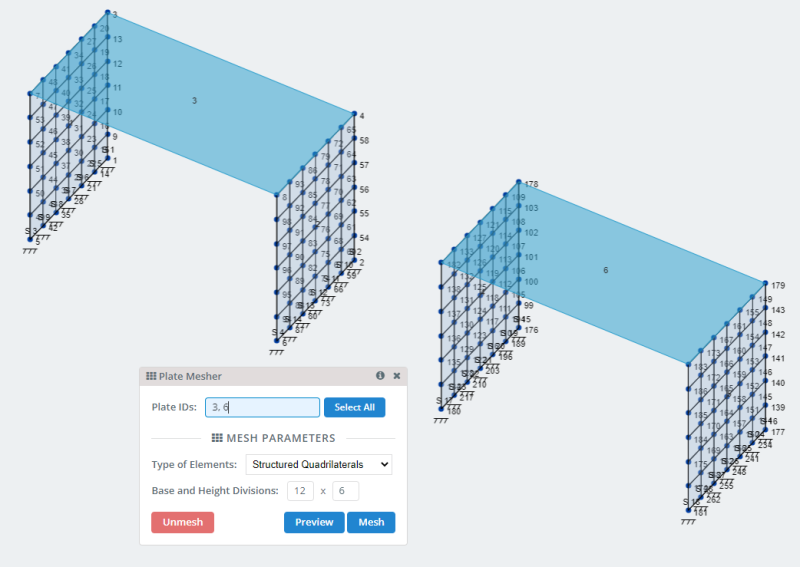
- Υλικά: Όπως είπαμε και πριν, Τα ορθότροπα υλικά έχουν διαφορετικές ιδιότητες κατά μήκος των κύριων αξόνων τους. Οι επόμενες εικόνες υποδεικνύουν τις εισόδους που πρέπει να ορίσουμε για το μοντέλο.


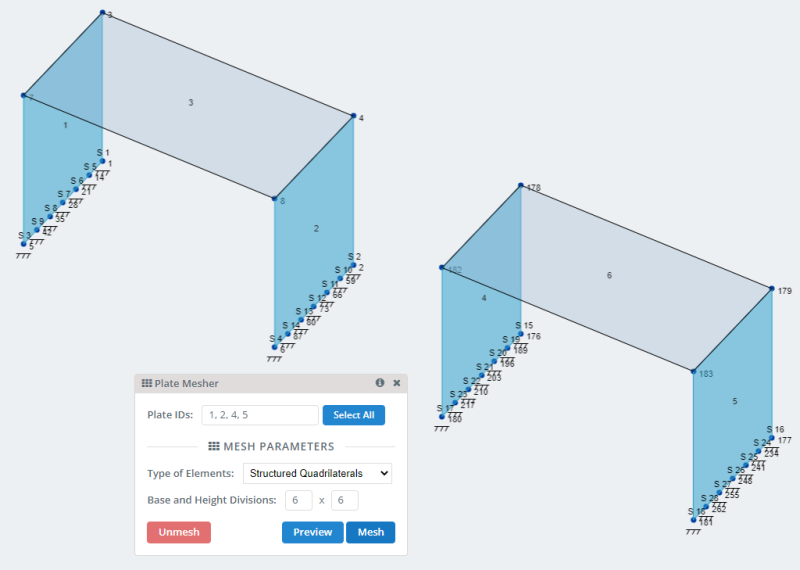
- Πλάκες: Μέσω κόμβων μοντέλων δημιουργούμε τις ορθογώνιες πλάκες. Δύο για τη μοντελοποίηση κάθετου τοίχου και ένα για το δάπεδο ή την πλάκα.

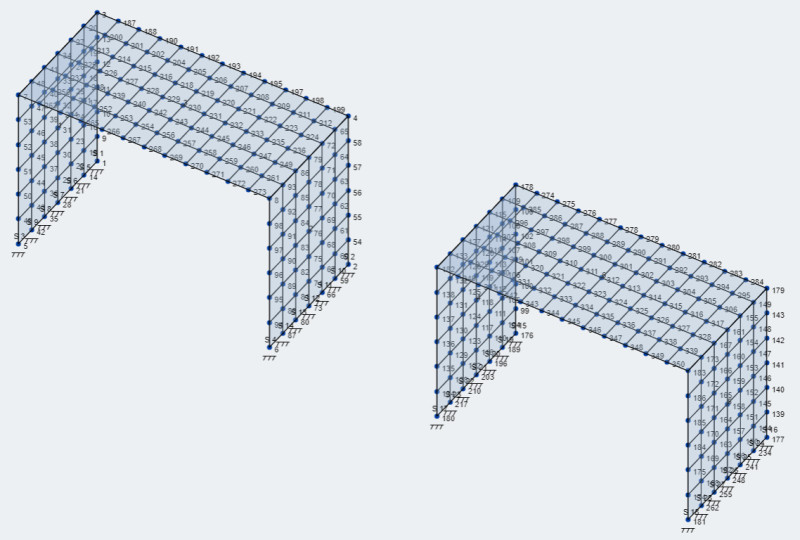
- Διχτυωτές πλάκες: Το SkyCiv έχει πολλές επιλογές για πλέγμα των πλακών και μπορείτε να το συμβουλευτείτε Δικτύωση του πιάτου σας . Για το μοντέλο μας, ας χρησιμοποιήσουμε την επιλογή του πλέγματος δομημένων τετραπλευρών.



- Καθορισμός φόρτισης αυτο-βάρους: Θα εξετάσουμε αυτό το φορτίο αυτο-βάρους μόνο για να καταγράψουμε τη γενική δομική συμπεριφορά της πλάκας.

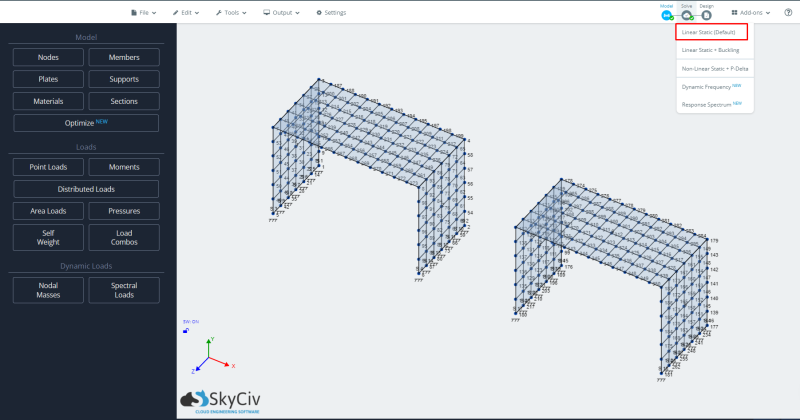
- Εκτελούμενη ανάλυση: Για να τρέξουμε το μοντέλο θα επιλέξουμε την περίπτωση γραμμικής στατικής ανάλυσης.

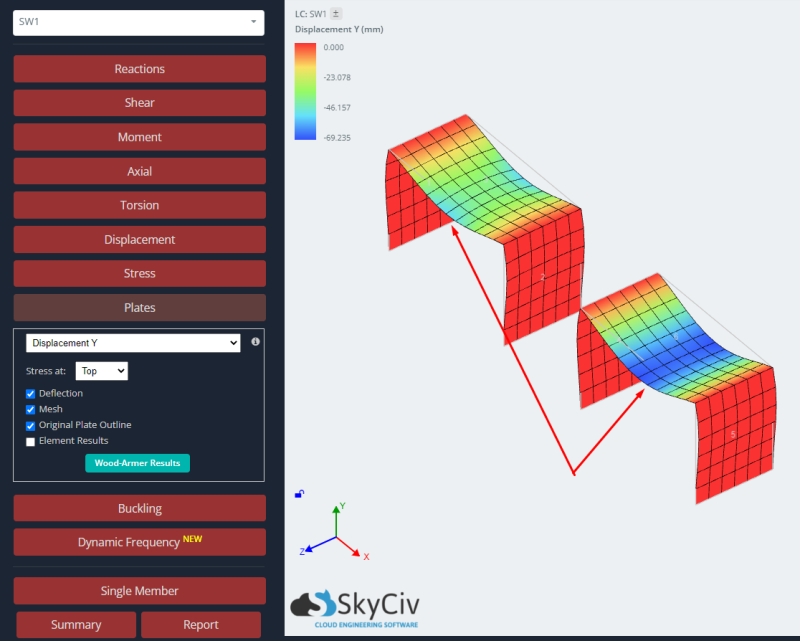
- Αποτελέσματα: Τελικά, Σε αυτό το σημείο μελετάμε τη δομική απόκριση και για τις δύο πλάκες, την ισότροπη και την ορθότροπη περίπτωση. Για περισσότερες λεπτομέρειες στην ανάγνωση των αποτελεσμάτων για την ανάλυση πλακών, μπορείτε να δείτε αυτό το άρθρο Αποτελέσματα ανάλυσης πλακών.

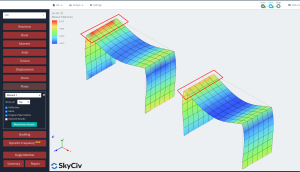
Να μελετήσει την ανταπόκριση και των δύο περιπτώσεων, Συγκρίνουμε τα αποτελέσματα της κατακόρυφης μετατόπισης και της ροπής κάμψης. Η ορθότροπη πλάκα παρουσιάζει μικρότερες παραμορφώσεις και μεγαλύτερες ροπές κάμψης από την ισότροπη περίπτωση. Μπορούμε να πούμε ότι η χρήση μιας ορθοτροπικής προσέγγισης θα μας δώσει ένα πιο άκαμπτο στοιχείο και αυτό θα επηρεάσει τα συνολικά και τοπικά αποτελέσματα σε μια ελαστική γραμμική ανάλυση.
Ξεκινήστε δωρεάν
Ολοκλήρωση παραγγελίας SkyCiv Structural 3D δωρεάν σήμερα για να πάρετε μια γεύση από το λογισμικό μας!
βιβλιογραφικές αναφορές:
- Τσαντροπάτλα, Τιρουπάθι Ρ & Belegundu, Ashok (2012). “Εισαγωγή στα πεπερασμένα στοιχεία στη μηχανική” 4η έκδοση, Pearson Education.
- Δ. Οι Jiang et al (1997). “Μοντελοποίηση πεπερασμένων στοιχείων σκληρυμένων και μη ορθοτροπικών πλακών”, Υπολογιστές & Structures Vol.63, Νο. 1, σελ. 105-117, Elsevier Science Ltd.
- Οι Torres Villavicencio et al (2013). “μονογραφικό έργο: Βοηθήματα σχεδίασης για συστήματα ρουλεμάν EMMEDUE πάνελ από οπλισμένο σκυρόδεμα με πυρήνα E.P.S (Σύστημα διογκωμένου πολυστυρενίου)”. Εθνικό Πανεπιστήμιο Μηχανικών.
- Όλες οι εικόνες λογισμικού λαμβάνονται από Λογισμικό SkyCiv Structural 3D Analysis