Κατά τη μοντελοποίηση μιας δομής στο SkyCiv Structural 3D, τα μέλη και οι συνδέσεις απλοποιούνται με κόμβους και γραμμές για μέλη. Αυτές οι γραμμές μεταξύ κόμβων τρέχουν πάντα μέσω του κεντροειδούς κάθε μέλους για απλότητα και συνέχεια. Στην πραγματικότητα, καταστάσεις προκύπτουν όταν το φορτίο που ενεργεί σε ένα μέλος δεν μπορεί να δικαιολογηθεί μέσω του κεντροειδούς του, αυτό είναι ένα εκκεντρικό φορτίο. Οι μηχανικοί πρέπει να σκεφτούν τα έκκεντρα φορτία κατά το σχεδιασμό των μελών επειδή η προσθήκη περιστροφής διατομής, ή Συστροφή, μπορώ, και πιθανότατα θα, επηρεάζει την οριακή κατάσταση της διατομής.
Για παράδειγμα: ένα σημείο φόρτωσης πάνω από ένα πρόβολο από πάνω, ή ένα κρεμαστό φορτίο από την πλευρά μιας δέσμης που συνδέεται με ενισχυτές. Ένα απλό γράφημα εκκεντρικών φορτίων και πώς να τα ερμηνεύσετε φαίνεται στο Σχήμα 1.
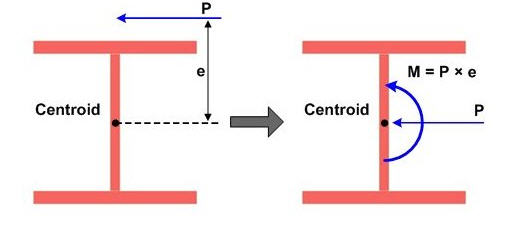
Φιγούρα 1: Παράδειγμα εκκεντρικού φορτίου σε διατομή σχήματος Ι
Πηγή: http://εγχειρίδιο.midasuser.com
Ας ρίξουμε μια ματιά σε ένα παράδειγμα στο SkyCiv Structural 3D και εφαρμόστε ένα εκκεντρικό σημείο φόρτωσης με δύο διαφορετικούς τρόπους. Πρώτα, ας υποθέσουμε ότι έχουμε μια δέσμη W14x22 που είναι 15 πόδια με έκκεντρο φορτίο σημείου στο μεσαίο άνοιγμα των 10 kips , ηθοποιία 12 ίντσες μακριά από το κέντρο. Θα υποθέσουμε ότι το φορτίο ενεργεί προς τα κάτω (-Και κατεύθυνση) και στην αριστερή πλευρά (+Z κατεύθυνση) του μέλους. Επίσης, θα υποθέσουμε ότι το αυτο-βάρος είναι απενεργοποιημένο, για απλότητα.
Κατά τη μοντελοποίηση ενός μέλους, βεβαιωθείτε ότι οι υποστηρίξεις σας είναι σωστές κατά τη μοντελοποίηση ενός εκκεντρικού φορτίου. Η ανάλυση δεν θα εκτελεστεί και με τα δύο υποστηρίγματα της δέσμης σας ως τρισδιάστατα ακροδέκτες επειδή καμία υποστήριξη δεν θα αντιστέκεται στην περιστροφή της διατομής. Στην περίπτωσή μας, Το στήριγμα πιο μακριά από την προέλευση είναι μόνο ένας 2D πείρος που επιτρέπει περιστροφή προς την κατεύθυνση X και Y, προέρχεται από κάθετη και οριζόντια παραμόρφωση. Ας ρίξουμε μια ματιά στο παράδειγμα του μέλους μας στον χώρο μοντελοποίησης 3D:
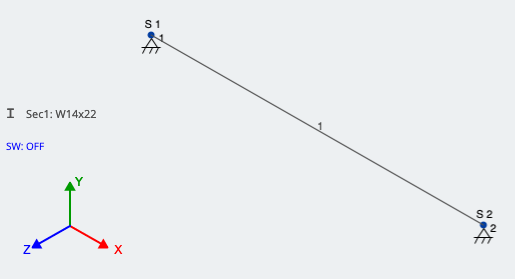
Τώρα, ας εξετάσουμε τις δύο μεθόδους λογιστικής για την εκκεντρότητα του φορτίου μας. Αναφερόμενοι στο Σχήμα 1, στην περίπτωσή μας:
\({Π} = {10} kips)
\({μι} = 12 ίντσες = 1 foot\)
Μέθοδος 1: Λογιστική εκκεντρότητας εφαρμόζοντας μια στιγμή
Όπως φαίνεται στο σχήμα 1, μπορούμε να εξηγήσουμε την εκκεντρότητα του φορτίου εφαρμόζοντας μια επιπλέον στιγμή στο κέντρο του μέλους. Αυτή η στιγμή εντοπίζεται λαμβάνοντας το σημειακό φορτίο πολλαπλασιαζόμενο με το βραχίονα ροπής, ή “μι”. Πρέπει ακόμη να λάβουμε υπόψη το ίδιο το σημείο φόρτωσης, οπότε θα υπάρξει (2) φορτώνει στην καθορισμένη τοποθεσία.
Στην περίπτωσή μας:
\({Μ} = {Π}*{μι}\)
\({Μ} = 10 kips * 1 πόδι = 10 kip-ft\)
Οπως αναφέρθηκε, αυτή η στιγμή εφαρμόζεται τώρα στην ίδια θέση κατά μήκος του μέλους με το εκκεντρικό σημείο φόρτωσης. Το SkyCiv αναγνωρίζει τη θετική στιγμή ως αριστερόστροφα γύρω από τον άξονα που εφαρμόζεται, που βρίσκεται γύρω από τον παγκόσμιο άξονα Χ στην περίπτωσή μας. Βλέπε σχήμα 3 από αυτά τα φορτία που εφαρμόστηκαν στο SkyCiv 3D:
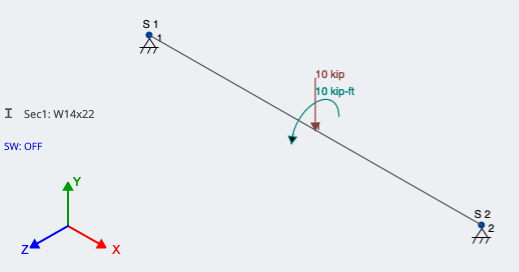
Φιγούρα 3: Μοντελοποίηση εκκεντρικού φορτίου εφαρμόζοντας μια επιπλέον στιγμή
Μέθοδος 2: Χρησιμοποιώντας άκαμπτους συνδέσμους
Μια άλλη μέθοδος είναι η χρήση άκαμπτων συνδέσμων. Άκαμπτοι σύνδεσμοι θεωρούνται ως φανταστικά μέλη που περιστρέφονται και μεταφράζονται με οτιδήποτε συνδέεται. Δεν εκτρέπονται μεταξύ των κόμβων τους και είναι εντελώς άκαμπτοι. Οι άκαμπτοι σύνδεσμοι αναγνωρίζονται στον χώρο μοντελοποίησης 3D ως ανοιχτό γκρι και έχουν α “Ρ” δίπλα τους, όπως φαίνεται στο σχήμα 4. Επειδή χρησιμοποιούνται περισσότερο για τη σύνδεση στοιχείων και φορτίων, χρειάζονται μέγεθος ή αναγνωριστικό ενότητας.
Για το παράδειγμά μας, Κόμβος 6 είναι στο midspan στο μέλος. Κόμβος 5 είναι στην ίδια συντεταγμένη Χ, αλλά 1.0 πόδια στην κατεύθυνση + Z; Κόμβος 5 είναι η πραγματική θέση του εκκεντρικού φορτίου.
Δημιουργήστε / σχεδιάστε ένα μέλος μεταξύ των δύο κόμβων, και να το ορίσετε ως άκαμπτο σύνδεσμο. Μπορείτε να το κάνετε πατώντας το Προχωρημένος μεταβείτε στο παράθυρο μέλους, μετά πηγαίνω Τύπος και να το αλλάξουμε σε Άκαμπτος σύνδεσμος. Μόλις εφαρμοστεί, το μέλος θα πρέπει να φαίνεται όπως περιγράφεται παραπάνω. Με το ένα άκρο να δείχνει την πραγματική θέση του εκκεντρικού φορτίου και το άλλο άκρο συνδεδεμένο με το μέλος στην κάθετη κατεύθυνση, το φορτίο μπορεί τελικά να εφαρμοστεί. Αυτό φαίνεται στο σχήμα 4; το κόκκινο βέλος δείχνει στον άκαμπτο σύνδεσμο:
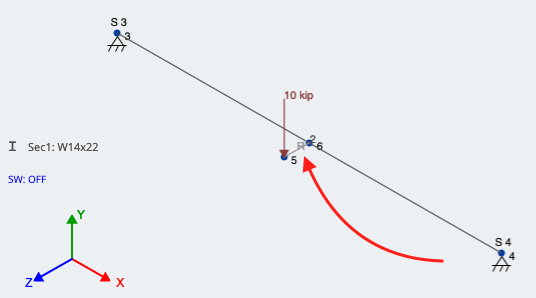
Φιγούρα 4: Χρησιμοποιώντας έναν άκαμπτο σύνδεσμο για τον υπολογισμό της εκκεντρότητας ενός σημείου φόρτωσης
Τελική σύγκριση και ανάλυση:
Ας εκτελέσουμε μια γραμμική στατική ανάλυση και να δούμε τα αποτελέσματα. Πρέπει να βλέπουμε την πτωτική δύναμη του 10 kips εκτός από ένα στρεπτικό στοιχείο στη θέση φόρτωσης. Και τα δυο
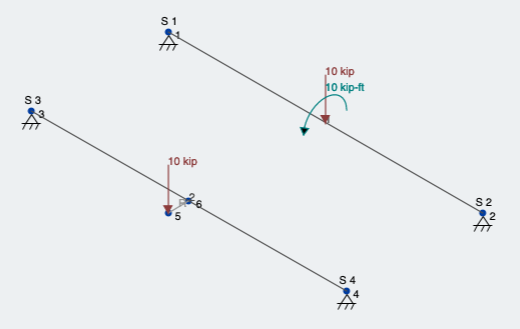
Φιγούρα 5: Και οι δύο συνθήκες φόρτωσης για εκκεντρικό φορτίο
Πρώτα, ας δούμε τα αποτελέσματα της αντίδρασης και της στιγμής (Φιγούρα 6):
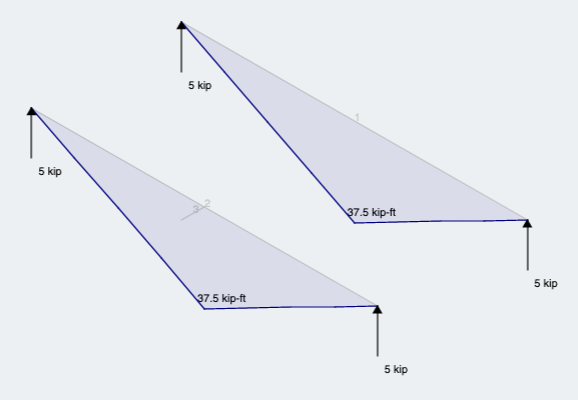
Φιγούρα 6: Αποτελέσματα αντιδράσεων και στιγμής και για τις δύο μεθόδους
Όπως αναμενόταν, βλέπουμε τι θα περιμέναμε από το ίδιο μέγεθος και το ίδιο μήκος κατά μήκος του μέλους, αλλά μέσω του κεντροειδούς.
Ακολούθως, λόγω της εκκεντρικότητας, μπορούμε να παρατηρήσουμε ότι και τα δύο μέλη δίνουν το ίδιο αποτέλεσμα και δείχνουν ότι το μέλος είναι ΕΠΙΣΗΣ βιώνει στρέψη (Φιγούρα 7):
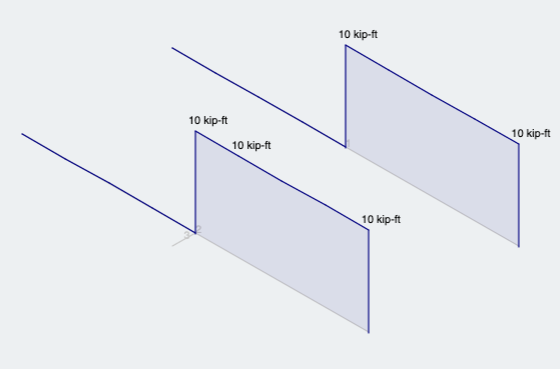
Φιγούρα 7: Αποτελέσματα ανάλυσης στρέψης και για τις δύο μεθόδους
Δομικός μηχανικός
BEng (Εμφύλιος)



