Αυτό το άρθρο εξετάζει δύο παραδείγματα σχεδίασης πλακών από οπλισμένο σκυρόδεμα, συμπεριλαμβανομένης της μονόδρομης και αμφίδρομης κάμψης. Ο κύριος στόχος είναι να συγκριθούν τα αποτελέσματα που προέκυψαν μεταξύ των υπολογισμών με το χέρι και της μονάδας σχεδίασης πλακών SkyCiv. Θα χρησιμοποιήσουμε τον Ευρωκώδικα 2 για Κατασκευές Οπλισμένου Σκυροδέματος.
Οι κατασκευαστικοί κώδικες έχουν παρόμοιες προσεγγίσεις κατά τον καθορισμό των τυπικών περιπτώσεων για πλάκες. Αν θέλετε να μάθετε περισσότερα για αυτό το θέμα, σας προτείνουμε να διαβάσετε τα παρακάτω άρθρα σχετικά με το σχεδιασμό πλακών Παράδειγμα σχεδίασης πλακών ACI και σύγκριση με το SkyCiv και Παράδειγμα σχεδίασης πλακών προτύπων Αυστραλίας AS3600 και σύγκριση με το SkyCiv
Παράδειγμα σχεδίασης πλάκας μονής κατεύθυνσης
Η πρώτη περίπτωση που πρέπει να αναλυθεί είναι ένα μικρό μονώροφο κτίριο (Φιγούρα 1, Φιγούρα 2) που έχει συμπεριφορά πλάκας που περιγράφεται ως προς μία κατεύθυνση.
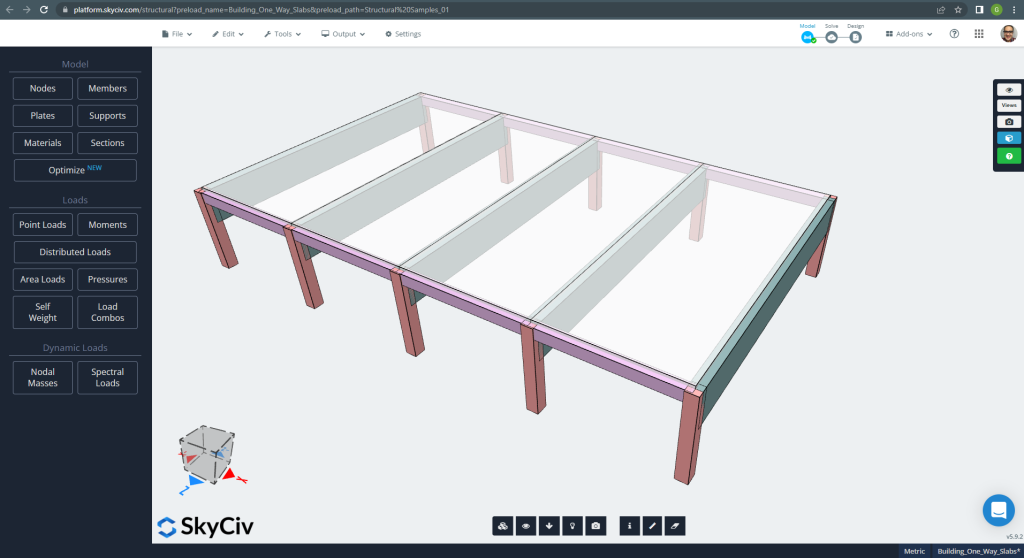
Φιγούρα 1. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
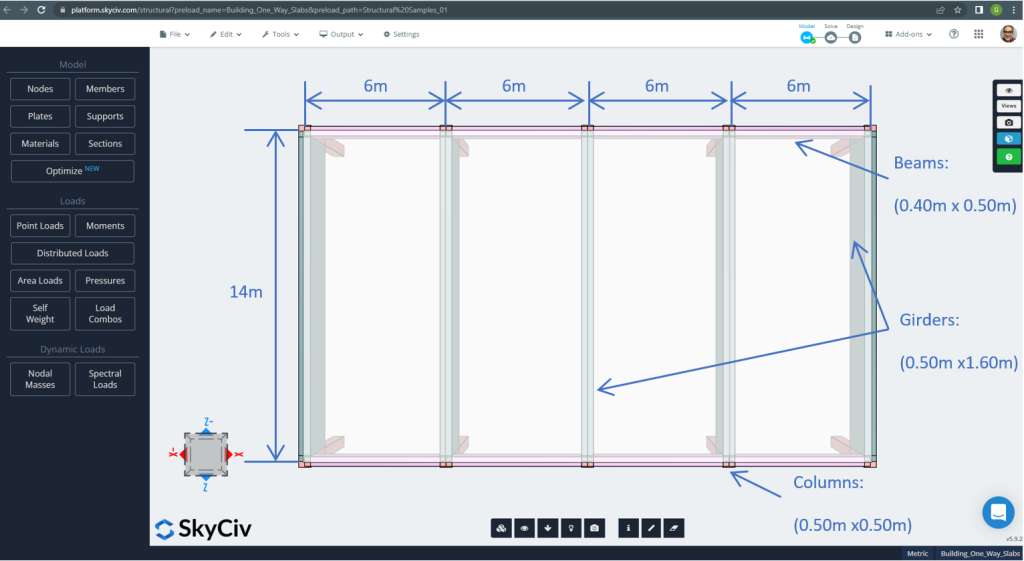
Φιγούρα 2. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου (διαστάσεις σχεδίου). (Δομικά 3D, SkyCiv Cloud Engineering).
Για το παράδειγμα πλάκας, Συνοψίζοντας, το υλικό, ιδιότητες στοιχείων, και φορτία που πρέπει να ληφθούν υπόψη :
- Ταξινόμηση τύπου πλάκας: Ενας – τρόπο συμπεριφοράς \(\frac{L_2}{L_1} > 2 ; \frac{14Μ}{6Μ}=2,33 > 2.00 \) Εντάξει!
- Επάγγελμα κτιρίου: Οικιστική χρήση
- Πάχος πλάκας \(αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{πλάκα}=0,25m)
- Πυκνότητα οπλισμένου σκυροδέματος \(\rho_w = 25 \frac{ΚΝ}{m^3}\)
- Χαρακτηριστική θλιπτική αντοχή σκυροδέματος στο 28 μέρες (C2530) \(fck = 25 MPa \)
- Πλάκα Αυτο-βάρος \(Νεκρό = rho_w φορές t_{πλάκα} = 25 \frac{ΚΝ}{m^3} \φορές 0,25m = 6.25 \frac {ΚΝ}{m^2}\)
- Υπερ-επιβεβλημένο νεκρό φορτίο \(SD = 3.0 \frac {ΚΝ}{m^2}\)
- Ζωντανό φορτίο \(L = 2.0 \frac {ΚΝ}{m^2}\)
Υπολογισμοί χειρός σύμφωνα με το EN-2
Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, θα υπολογίσουμε την απαιτούμενη ράβδο οπλισμένου χάλυβα χρησιμοποιώντας την αναφορά του προτύπου του Ευρωκώδικα. Λαμβάνουμε πρώτα τη συνολική συντελεστή ροπής κάμψης που πρέπει να πραγματοποιηθεί από τη λωρίδα ενιαίου πλάτους της πλάκας.
- Νεκρό φορτίο, \(g = (3.0 + 6.25) \frac{ΚΝ}{m^2} \φορές 1 m = 9.25 \frac{ΚΝ}{Μ}\)
- Ζωντανό φορτίο, \(q = (2.0) \frac{ΚΝ}{m^2} \φορές 1 m = 2.0 \frac{ΚΝ}{Μ}\)
- Απόλυτο φορτίο, \(Fd = 1,35 φορές g + 1.5\φορές q = (1.35\φορές 9.25 + 1.5\φορές 2.0)\frac{ΚΝ}{Μ} =15,5 φράκ{ΚΝ}{Μ} \)
Πριν από την απόκτηση της περιοχής οπλισμού χάλυβα, πρέπει να ελέγξουμε τις αναλογίες βάθους με αποτέλεσμα το άνοιγμα. Δύο βασικές περιπτώσεις:
| Δομικό Σύστημα | Βασικός λόγος βάθους αποτελεσματικού ανοίγματος | ||
|---|---|---|---|
| Συντελεστής για δομικό σύστημα Κ | Το σκυρόδεμα έχει μεγάλη ένταση %(\(\rho = 1.5 )\) | Το σκυρόδεμα έχει ελαφρά καταπονηθεί %(\(\rho = 0.5 )\) | |
| 1. Τελικό άνοιγμα συνεχούς δοκού ή μονόδρομης συνεχούς πλάκας ή διπλής κατεύθυνσης πλάκας συνεχούς σε μια μεγάλη πλευρά | 1.3 | 18 | 26 |
| 2. Εσωτερικό άνοιγμα συνεχούς δοκού ή πλάκας μονής ή διπλής κατεύθυνσης | 1.5 | 20 | 30 |
Η πιο κρίσιμη περίπτωση είναι για το νούμερο ένα, Έτσι, επιλέγουμε μια αναλογία 26.
- \(αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ελάχ}= frac{μεγάλο}{ΞΕΡΩ}+εξώφυλλο+0,5κουκκίδα_{διάμετρος}= frac{6Μ}{26}+0.025m+0,5 φορές 12mm=0,26m \) ~ \(0.25Μ). Το συνολικό πάχος εξακολουθεί να είναι επαρκές, Εντάξει!
Τώρα, είναι καιρός να χρησιμοποιήσετε το τραπέζι για μονόδρομες συνεχείς πλάκες:
| Συνθήκη τερματισμού υποστήριξης | Στην αρχή εσωτερική υποστήριξη | Στο μέσο των εσωτερικών ανοιγμάτων | Στα εσωτερικά στηρίγματα | ||||
|---|---|---|---|---|---|---|---|
| Καρφιτσώθηκε | Συνεχής | ||||||
| Εξωτερική υποστήριξη | Σχεδόν στη μέση του ακραίου ανοίγματος | Τερματίστε την υποστήριξη | Τελικό διάστημα | ||||
| Στιγμή | 0 | 0.086FL | – | 0.075FL | – | 0.063FL | – |
| 0.04FL | 0.086FL | 0.063FL | |||||
| Κουρεύω | 0.4φά | – | – | – | |||
| 0.46φά | 0.6φά | 0.5φά | |||||
Οπου:
- Το L είναι το αποτελεσματικό διάστημα
- F είναι το συνολικό τελικό φορτίο στο άνοιγμα (1.35Gk + 1.5Qk; Το Gk είναι το νεκρό φορτίο και το Qk το ζωντανό φορτίο, αντίστοιχα)
Θα εξηγηθεί μόνο μία περίπτωση (συνεχής τελική υποστήριξη) και τα υπόλοιπα θα φανούν στον παρακάτω πίνακα.
- \(F=Fd φορές L = 15.5 \frac{ΚΝ}{Μ} \φορές 6m = 93.0 ΚΝ \)
- \(M=0,04FL=0,04 φορές 93.0 kN φορές 6m= -22.32{ΚΝ}{Μ}\)
- \(d = 230 mm \)
- \(K=frac{Μ}{{σι}{d^2}{φά_{ck}}}= frac{22.32\φορές 10^6 {Ν}{χιλ}}{{1000χιλ}\φορές{(230 χιλ)^ 2}\φορές {25 \frac{Ν}{mm^2}}}=0,016877)
- \(l_a = 0.95 \)
- \(z=l_a φορές d = 0,95 φορές 230mm = 218.50 mm)
- \(A_s = frac{Μ}{{0.87}{φά_{yk}}{με}}= frac{22.32\φορές 10^6 {Ν}{χιλ}}{0.87\φορές 500 {Ν}{mm^2} \φορές {218.50χιλ} = 234.83 mm^2 }\)
- \(ΕΝΑ_{μικρό,ελάχ}=0,0013{σι}{ρε}=0,0013 φορές 1000 mm φορές 230 mm =299 mm^2)
- \(ΕΝΑ_{αγ}=μέγ(Οπως και, ΕΝΑ_{μικρό,ελάχ}) = μέγ(234.83, 299) mm^2 = 299 mm^2 \)
| Στιγμές | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| Τιμή M, kN-m | 22.32 | 35.15 | 41.85 | 48.00 | 35.15 | 35.15 |
| κ | 0.0168 | 0.0266 | 0.03164 | 0.0362 | 0.0266 | 0.0266 |
| με, χιλ | 218.50 | 218.50 | 218.50 | 218.50 | 218.50 | 218.50 |
| \(Οπως και, mm^2) | 234.83 | 369.815 | 440.31 | 505.011 | 369.815 | 369.815 |
| \(ΕΝΑ_{μικρό,ελάχ},mm^2) | 299.00 | 299.00 | 299.00 | 299.00 | 299.00 | 299.00 |
| \(ΕΝΑ_{αγ} {mm^2}\) | 299.00 | 369.815 | 440.31 | 505.011 | 369.815 | 369.815 |
Η επόμενη κίνηση είναι ο υπολογισμός του χάλυβα οπλισμού οπλισμού χρησιμοποιώντας τη μονάδα σχεδίασης πλακών στο SkyCiv. Σας παρακαλούμε, συνεχίστε να διαβάζετε την παρακάτω ενότητα!.
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
Αποτελέσματα ενότητας σχεδίασης πλακών SkyCiv S3D
Αυτή η ενότητα ασχολείται με την απόκτηση της περιοχής ενίσχυσης από χάλυβα αλλά μόνο με τη χρήση του λογισμικού, ο Ενότητα σχεδίασης πιάτων. Με συνοπτικό τρόπο, θα δείξουμε μόνο τα αποτελέσματα ή σημαντικές πληροφορίες μέσω εικόνων.
Πριν από την ανάλυση του μοντέλου, πρέπει να ορίσουμε ένα μέγεθος πλέγματος πλάκας. Μερικές αναφορές (2) προτείνετε ένα μέγεθος για το στοιχείο κελύφους του 1/6 του μικρού διαστήματος ή 1/8 του μεγάλου εύρους, το μικρότερο από αυτά. Ακολουθώντας αυτή την τιμή, έχουμε \(\frac{L2}{6}= frac{6Μ}{6} = 1 m \) ή \(\frac{L1}{8}= frac{14Μ}{8}=1,75μ \); παίρνουμε 1 m ως μέγιστο συνιστώμενο μέγεθος και 0,50 m εφαρμοσμένο μέγεθος ματιών.
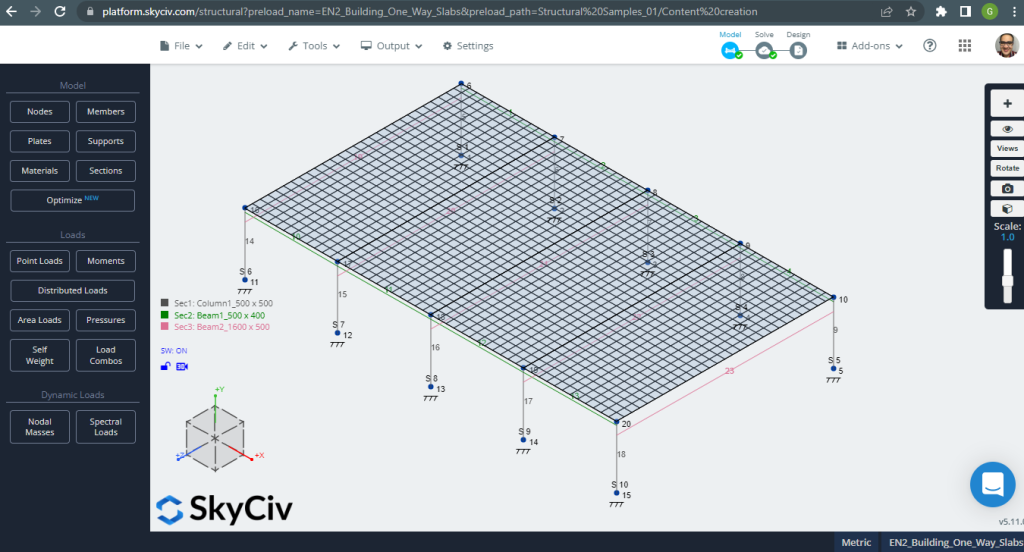
Φιγούρα 3. Διχτυωτό πιάτο. (Δομικά 3D, SkyCiv Cloud Engineering).
Μόλις βελτιώσαμε το αναλυτικό δομικό μας μοντέλο, κάνουμε γραμμική ελαστική ανάλυση. Κατά το σχεδιασμό πλακών, πρέπει να ελέγξουμε αν η κατακόρυφη μετατόπιση είναι μικρότερη από τη μέγιστη επιτρεπόμενη από τον κωδικό. Ευρωκώδικας 2 καθιέρωσε μια μέγιστη λειτουργικότητα κατακόρυφη μετατόπιση του \(\frac{μεγάλο}{250}= frac{6000χιλ}{250}=24,0 mm).
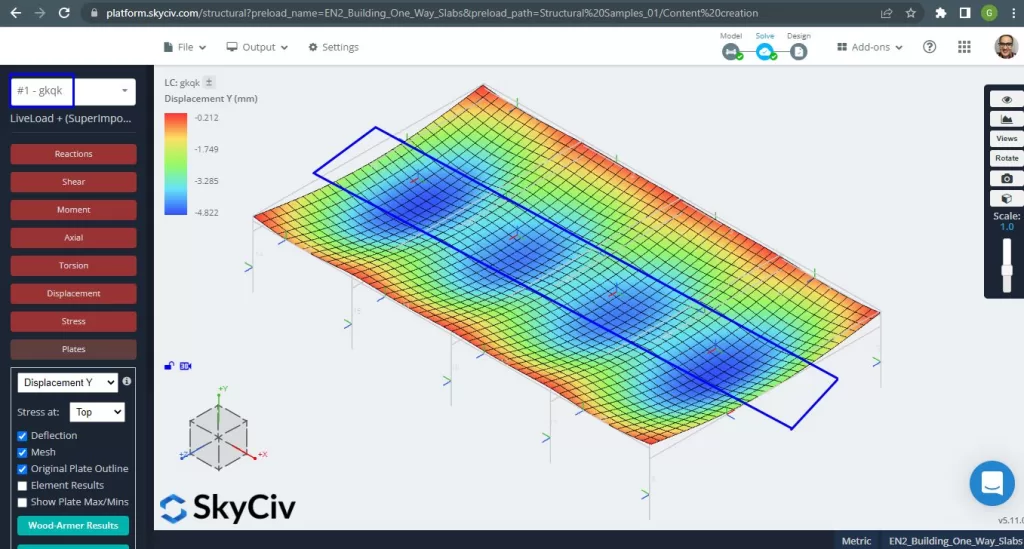
Φιγούρα 4. Κατακόρυφη μετατόπιση, μέγιστες τιμές στο κέντρο των ανοιγμάτων. (Δομικά 3D, SkyCiv Cloud Engineering).
Σύγκριση της μέγιστης κατακόρυφης μετατόπισης με την τιμή που αναφέρεται στον κωδικό, η ακαμψία της πλάκας είναι επαρκής. \(4.822 χιλ < 24.00mm).
Οι μέγιστες ροπές στα ανοίγματα της πλάκας βρίσκονται για θετικές στο κέντρο και για αρνητικές στα εξωτερικά και εσωτερικά στηρίγματα. Ας δούμε τις τιμές αυτών των στιγμών στις παρακάτω εικόνες.
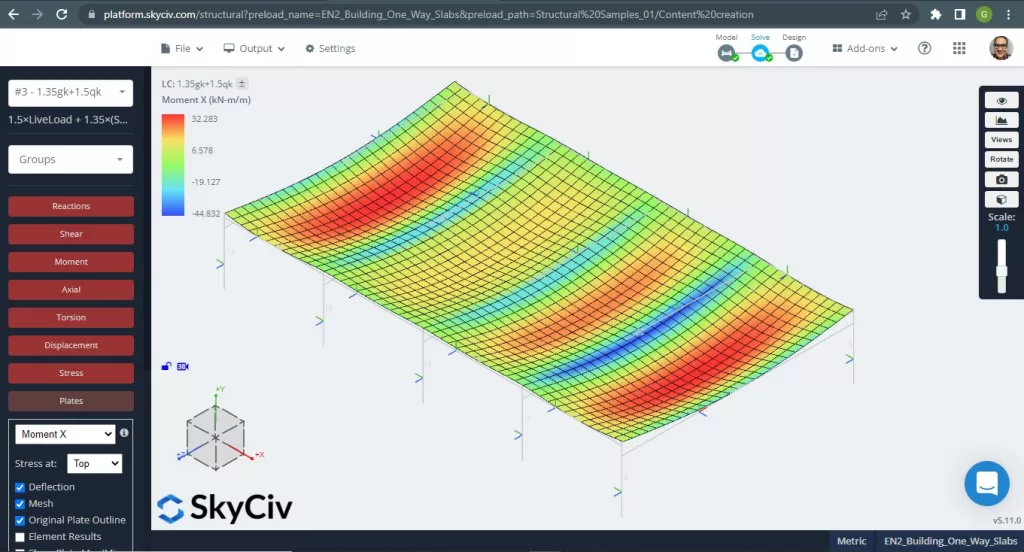
Φιγούρα 5. Ροπές κάμψης προς Χ κατεύθυνση. (Δομικά 3D, SkyCiv Cloud Engineering).
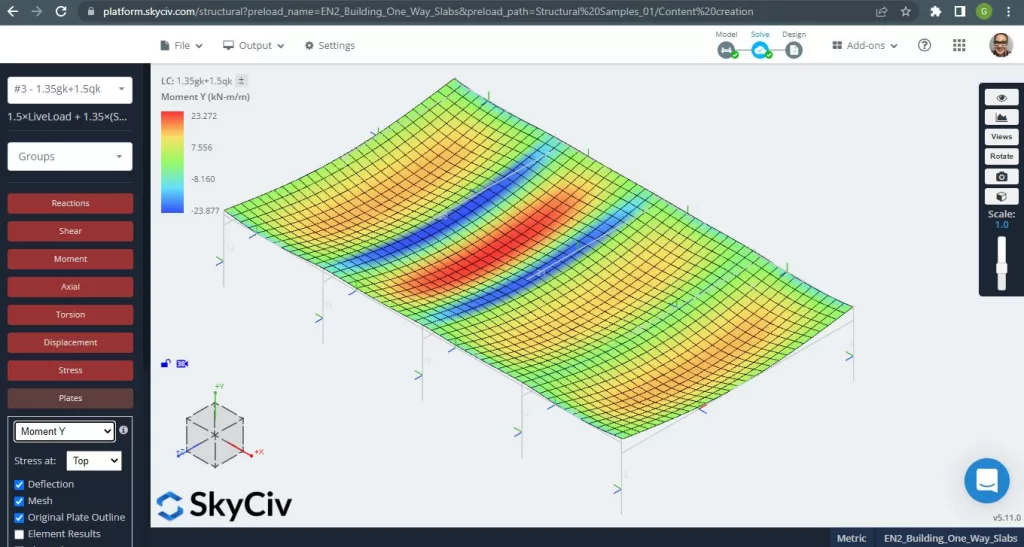
Φιγούρα 6. Ροπές κάμψης προς την κατεύθυνση Υ. (Δομικά 3D, SkyCiv Cloud Engineering).
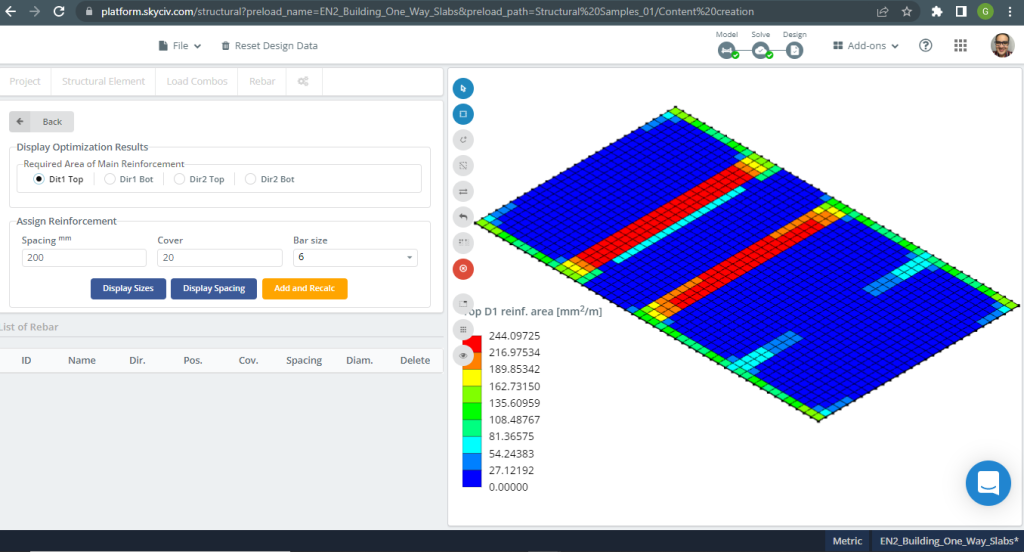
Φιγούρα 7. Χάλυβας Ενίσχυση για κατεύθυνση Χ στην κορυφή. (Δομικά 3D, SkyCiv Cloud Engineering).
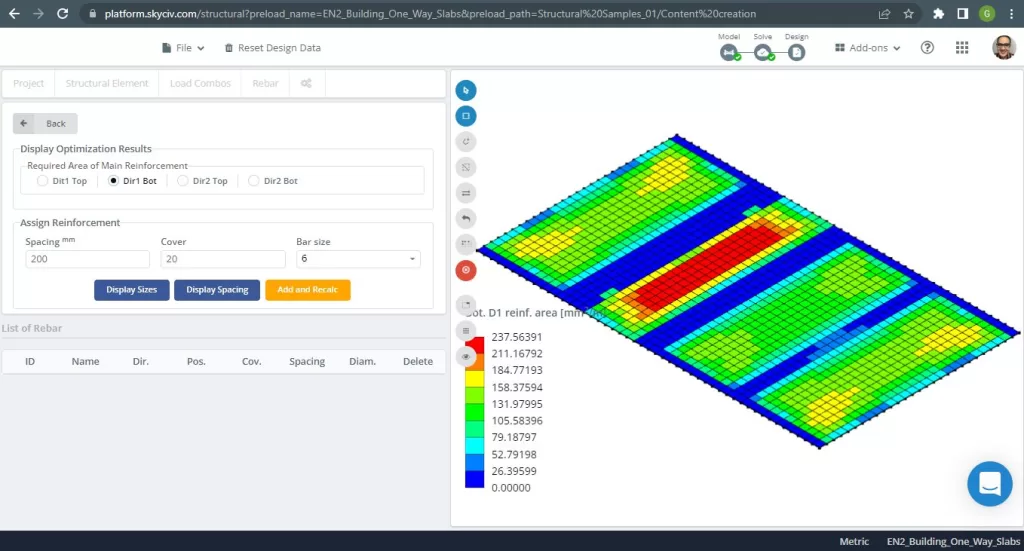
Φιγούρα 8. Χάλυβας Ενίσχυση για κατεύθυνση Χ στο κάτω μέρος. (Δομικά 3D, SkyCiv Cloud Engineering).
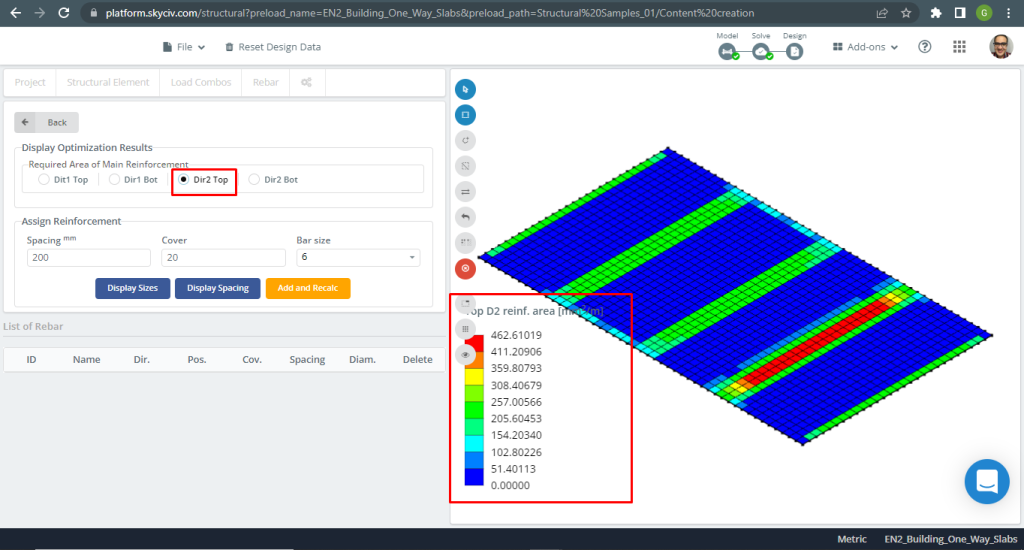
Φιγούρα 9. Χάλυβας Οπλισμός για κατεύθυνση Υ στο πάνω μέρος. (Δομικά 3D, SkyCiv Cloud Engineering).
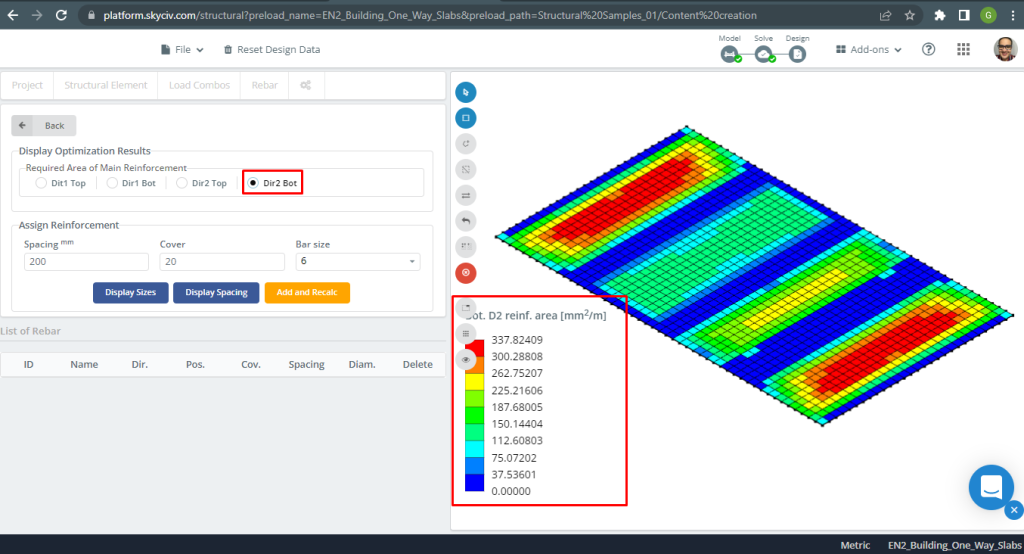
Φιγούρα 10. Χάλυβας Ενίσχυση για κατεύθυνση Υ στο κάτω μέρος. (Δομικά 3D, SkyCiv Cloud Engineering).
Σύγκριση αποτελεσμάτων
Το τελευταίο βήμα σε αυτό το παράδειγμα σχεδίασης πλάκας μονής κατεύθυνσης είναι η σύγκριση της επιφάνειας του χαλύβδινου οπλισμού που ελήφθη με ανάλυση S3D (τοπικούς άξονες “2”) και υπολογισμοί χειρός.
| Στιγμές και περιοχή χάλυβα | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| \(ΕΝΑ_{αγ, HandCalcs} {mm^2}\) | 299.00 | 369.82 | 440.31 | 505.011 | 369.82 | 369.82 |
| \(ΕΝΑ_{αγ, S3D} {mm^2}\) | 308.41 | 337.82 | 462.61 | 462.61 | 262.75 | 308.41 |
| \(\Δέλτα_{διαφ}\) (%) | 3.051 | 8.653 | 4.820 | 8.400 | 28.95 | 16.610 |
Μπορούμε να δούμε ότι τα αποτελέσματα των τιμών είναι πολύ κοντά μεταξύ τους. Αυτό σημαίνει ότι οι υπολογισμοί είναι σωστοί!
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
Παράδειγμα σχεδίασης πλακών διπλής κατεύθυνσης
Το SkyCiv 3D Plate Design Module είναι ένα ισχυρό λογισμικό που μπορεί να αναλύσει και να σχεδιάσει οποιοδήποτε τύπο κτιρίου μπορείτε να απεικονίσετε. Για το δεύτερο παράδειγμα σχεδιαστικής πλάκας, αποφασίσαμε να εκτελέσουμε ένα σύστημα επίπεδης πλάκας (φιγούρα 11).
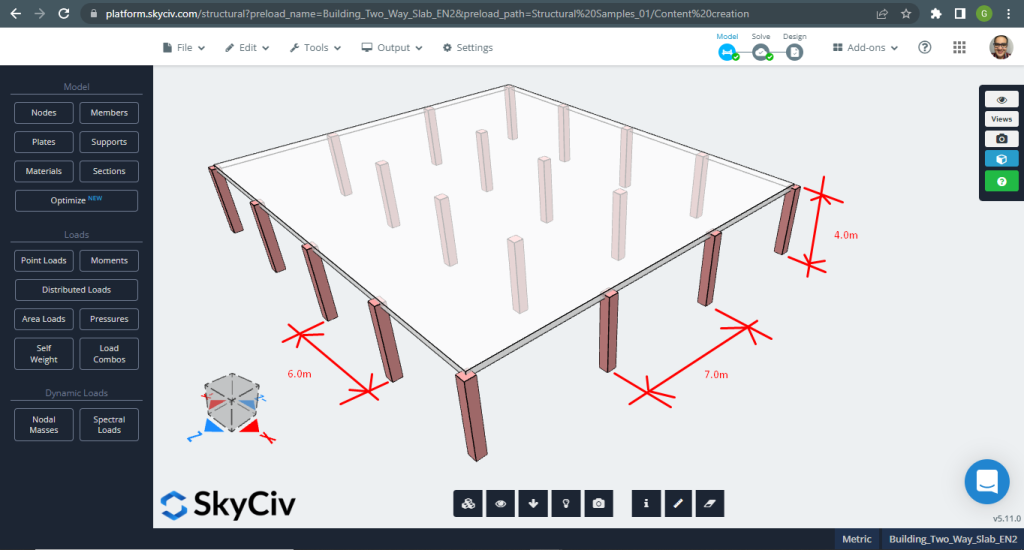
Φιγούρα 11. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
Για το παράδειγμα πλάκας, Συνοψίζοντας, το υλικό, ιδιότητες στοιχείων, και φορτία που πρέπει να ληφθούν υπόψη :
- Ταξινόμηση τύπου πλάκας: Δύο – τρόπο συμπεριφοράς \(\frac{L_2}{L_1} \ο 2 ; \frac{7Μ}{6Μ}=1,17 le 2.00 \) Εντάξει!
- Επάγγελμα κτιρίου: Οικιστική χρήση
- Πάχος πλάκας \(αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{πλάκα}=0,30m)
- Πυκνότητα οπλισμένου σκυροδέματος \(\rho_w = 25 \frac{ΚΝ}{m^3}\)
- Χαρακτηριστική θλιπτική αντοχή σκυροδέματος στο 28 μέρες (C2530) \(fck = 25 MPa \)
- Πλάκα Αυτο-βάρος \(Νεκρό = rho_w φορές t_{πλάκα} = 25 \frac{ΚΝ}{m^3} \φορές 0,30m = 7.5 \frac {ΚΝ}{m^2}\)
- Υπερ-επιβεβλημένο νεκρό φορτίο \(SD = 3.0 \frac {ΚΝ}{m^2}\)
- Ζωντανό φορτίο \(L = 2.0 \frac {ΚΝ}{m^2}\)
Υπολογισμοί με το χέρι σύμφωνα με το EN-2
Το πρώτο βήμα είναι ο καθορισμός του συνολικού τελικού φορτίου:
- Νεκρό φορτίο, \(g = (3.0 + 7.5) \frac{ΚΝ}{m^2} \φορές 7 m = 73.50 \frac{ΚΝ}{Μ}\)
- Ζωντανό φορτίο, \(q = (2.0) \frac{ΚΝ}{m^2} \φορές 7 m = 14.00 \frac{ΚΝ}{Μ}\)
- Απόλυτο φορτίο, \(Fd = 1,35 φορές g + 1.5\φορές q = (1.35\φορές 73.50 + 1.5\φορές 14.00)\frac{ΚΝ}{Μ} =120.225 \frac{ΚΝ}{Μ} \)
Για υπολογισμό με το χέρι, η δομή πρέπει να χωριστεί σε μια σειρά ισοδύναμων πλαισίων. Μπορούμε να χρησιμοποιήσουμε τις ακόλουθες μεθόδους για να επιτύχουμε αυτόν τον στόχο:
- Κατανομή ροπών (Μέθοδος Hardy Cross) για ανάλυση πλαισίου.
- Μέθοδος ακαμψίας για ανάλυση πλαισίου στον υπολογιστή. Δοκιμάστε μας Υπολογιστής μήτρας ακαμψίας.
- Μια απλοποιημένη μέθοδος που χρησιμοποιεί τους συντελεστές ροπών για μονόδρομη κατεύθυνση προσαρμοσμένη στις ακόλουθες απαιτήσεις (Επιλέξαμε αυτή τη μέθοδο λόγω της απλότητας του μοντέλου που αναλύθηκε):
- Η πλευρική σταθερότητα δεν εξαρτάται από τις συνδέσεις πλάκας-κολώνας (Δεν αναλύουμε το κτίριο για πλευρικά φορτία);
- Υπάρχουν τουλάχιστον τρεις σειρές πλαισίων με περίπου ίσο άνοιγμα προς την κατεύθυνση που εξετάζουμε (Έχουμε τέσσερις και τρεις σειρές πάνελ και στις δύο κύριες κατευθύνσεις);
- Το μέγεθος του κόλπου υπερβαίνει \(30m^2) (Η περιοχή του μοντέλου μας είναι \(42m^2)
Το πάχος που επιλέχθηκε για το παράδειγμα πλάκας είναι μεγαλύτερο από τη μέγιστη ελάχιστη τιμή για αντοχή στη φωτιά που υποδεικνύεται στον παρακάτω πίνακα.
| Τυπική αντοχή στη φωτιά | Ελάχιστες διαστάσεις (χιλ) | |
|---|---|---|
| Πάχος πλάκας, hs | Απόσταση άξονα, ένα | |
| REI 60 | 180 | 15 |
| REI 90 | 200 | 25 |
| REI 120 | 200 | 35 |
| REI 240 | 200 | 50 |
Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, θα αναπτύξουμε μόνο τους υπολογισμούς για τη διαμήκη κατεύθυνση και τη λωρίδα στήλης (μη διστάσετε να υπολογίσετε για άλλη κατεύθυνση, το εγκάρσιο, και για μεσαίες λωρίδες). Πριν προχωρήσουμε βαθιά στους αριθμούς, πρώτα πρέπει να χωρίσουμε σε λωρίδες: μέση και στήλη. (Για περισσότερες λεπτομέρειες σχετικά με τις λωρίδες σχεδίασης, ελέγξτε αυτό το άρθρο του SkyCiv: Πλάκες σχεδίασης με ACI-318).
- Πλάτος λωρίδας στήλης: \(6m/4 = 1,50 m)
- Μεσαίο πλάτος λωρίδας: \(7Μ – 2\times 1.50m = 4.0m\)
Το EC2 επιτρέπει την εκχώρηση ροπών σε κάθε λωρίδα σχεδίασης σύμφωνα με τον παρακάτω πίνακα
| Λωρίδα στήλης | Μεσαία λωρίδα | |
|---|---|---|
| Αρνητική ροπή στην ακραία στήλη | 100% αλλά όχι περισσότερο από \(0.17{είναι}{d^2}{φά_{ck}}\) | 0 |
| Αρνητική στιγμή στην εσωτερική στήλη | 60-80% | 40-20% |
| Θετική στιγμή στο διάστημα | 50-70% | 50-30% |
Επιλέξαμε τα ποσοστά των ροπών για τη λωρίδα στήλης που αναλύεται:
- Αρνητική ροπή στην ακραία στήλη: 100%.
- Αρνητική στιγμή στην εσωτερική στήλη: 80%
- Θετική στιγμή στο διάστημα: 70%
Υπολογισμός ροπών συνολικών λωρίδων σχεδίασης:
| Συνθήκη τερματισμού υποστήριξης | Στην αρχή εσωτερική υποστήριξη | Στο μέσο των εσωτερικών ανοιγμάτων | Στα εσωτερικά στηρίγματα | ||||
|---|---|---|---|---|---|---|---|
| Καρφιτσώθηκε | Συνεχής | ||||||
| Εξωτερική υποστήριξη | Σχεδόν στη μέση του ακραίου ανοίγματος | Τερματίστε την υποστήριξη | Τελικό διάστημα | ||||
| Στιγμή | 0 | 0.086FL | – | 0.075FL | – | 0.063FL | – |
| 0.04FL | 0.086FL | 0.063FL | |||||
| Κουρεύω | 0.4φά | – | – | – | |||
| 0.46φά | 0.6φά | 0.5φά | |||||
Οπου:
- Το L είναι το αποτελεσματικό διάστημα
- F είναι το συνολικό τελικό φορτίο στο άνοιγμα (1.35Gk + 1.5Qk; Το Gk είναι το νεκρό φορτίο και το Qk το ζωντανό φορτίο, αντίστοιχα)
Θα εξηγηθεί μόνο μία περίπτωση (συνεχής τερματική υποστήριξη) και τα υπόλοιπα θα φανούν στον παρακάτω πίνακα.
- \(F=Fd φορές L = 120.225 \frac{ΚΝ}{Μ} \φορές 6m = 721.35 ΚΝ \)
- \(M=0,04FL=0,04 φορές 721.35 kN φορές 6m= -173.124 {ΚΝ}{Μ}\)
- \(d = 280 mm \)
- \(K=frac{Μ}{{σι}{d^2}{φά_{ck}}}= frac{173.124\φορές 10^6 {Ν}{χιλ}}{{1500χιλ}\φορές{(280 χιλ)^ 2}\φορές {25 \frac{Ν}{mm^2}}}=0,012637)
- \(l_a = 0.95 \)
- \(z=l_a \times d = 0.95\times 280mm = 266.0 mm)
- \(A_s = frac{Μ}{{0.87}{φά_{yk}}{με}}= frac{173.124\φορές 10^6 {Ν}{χιλ}}{0.87\φορές 500 {Ν}{mm^2} \φορές {266.0χιλ} = 214.0523 mm^2 }\)
- \(ΕΝΑ_{μικρό,ελάχ}=0,0013{σι}{ρε}=0.0013\times 1500mm \times 280 mm =546 mm^2\)
- \(ΕΝΑ_{αγ}=μέγ(Οπως και, ΕΝΑ_{μικρό,ελάχ}) = μέγ(234.83, 546) mm^2 = 299 mm^2 \)
| Στιγμές | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| Τιμή M, kN-m | 173.124 | 191.125 | 260.064 | 298.281 | 191.125 | 218.429 |
| κ | 0.05897 | 0.06500 | 0.0884 | 0.101 | 0.06500 | 0.0743 |
| με, χιλ | 266.00 | 266.00 | 266.00 | 266.00 | 266.00 | 266.00 |
| \(Οπως και, mm^2) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
| \(ΕΝΑ_{μικρό,ελάχ},mm^2) | 546.00 | 546.00 | 546.00 | 546.00 | 546.00 | 546.00 |
| \(ΕΝΑ_{αγ} {mm^2}\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
Η επόμενη κίνηση είναι ο υπολογισμός του χάλυβα οπλισμού οπλισμού χρησιμοποιώντας τη μονάδα σχεδίασης πλακών στο SkyCiv. Σας παρακαλούμε, συνεχίστε να διαβάζετε την παρακάτω ενότητα!
Αποτελέσματα ενότητας σχεδίασης πλακών SkyCiv S3D
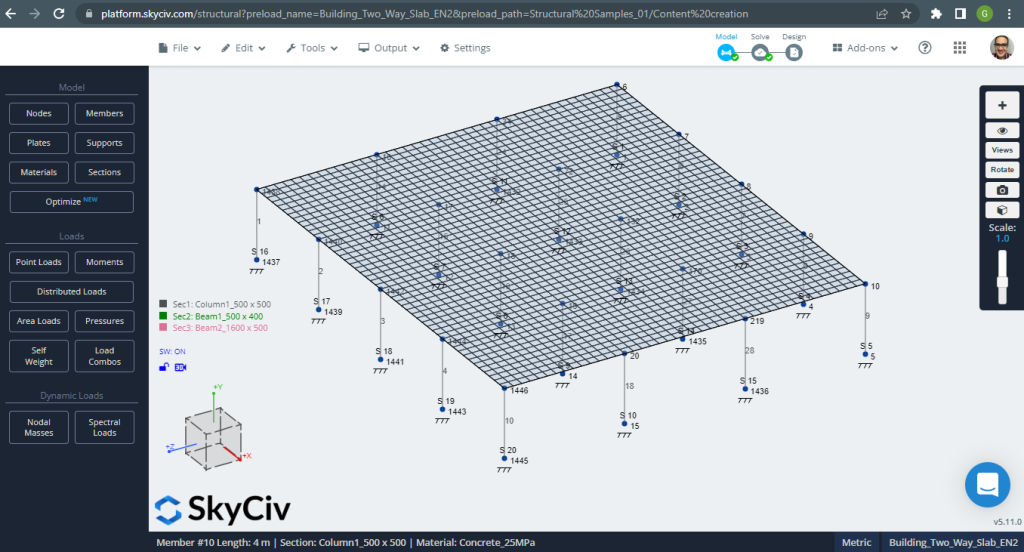
Φιγούρα 12. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
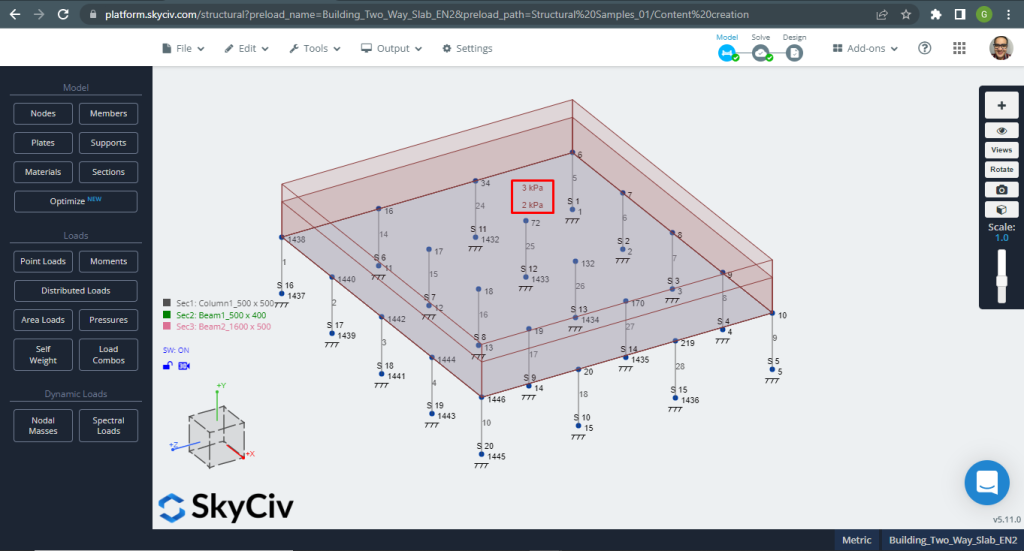
Φιγούρα 13. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
Κατά το σχεδιασμό πλακών, πρέπει να ελέγξουμε αν η κατακόρυφη μετατόπιση είναι μικρότερη από τη μέγιστη επιτρεπόμενη από τον κωδικό. Ο Ευρωκώδικας καθιέρωσε μια μέγιστη κατακόρυφη μετατόπιση της λειτουργικότητας του \(\frac{μεγάλο}{250}= frac{6000χιλ}{250}=24,0 mm).
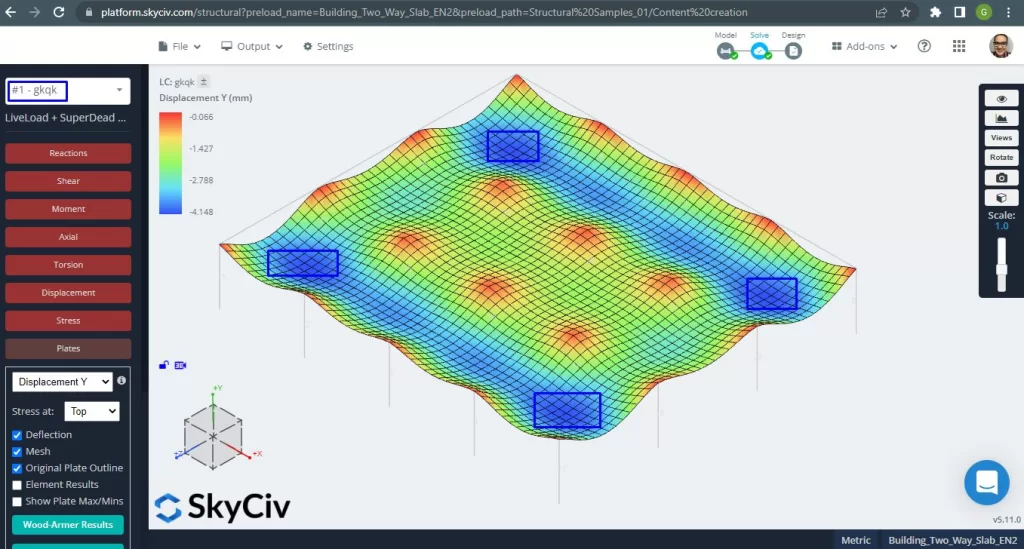
Φιγούρα 14. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
Η παραπάνω εικόνα μας δίνει την κατακόρυφη μετατόπιση. Η μέγιστη τιμή είναι -4,148mm όντας μικρότερη από τη μέγιστη επιτρεπόμενη των -24mm. Επομένως, η ακαμψία της πλάκας είναι επαρκής.
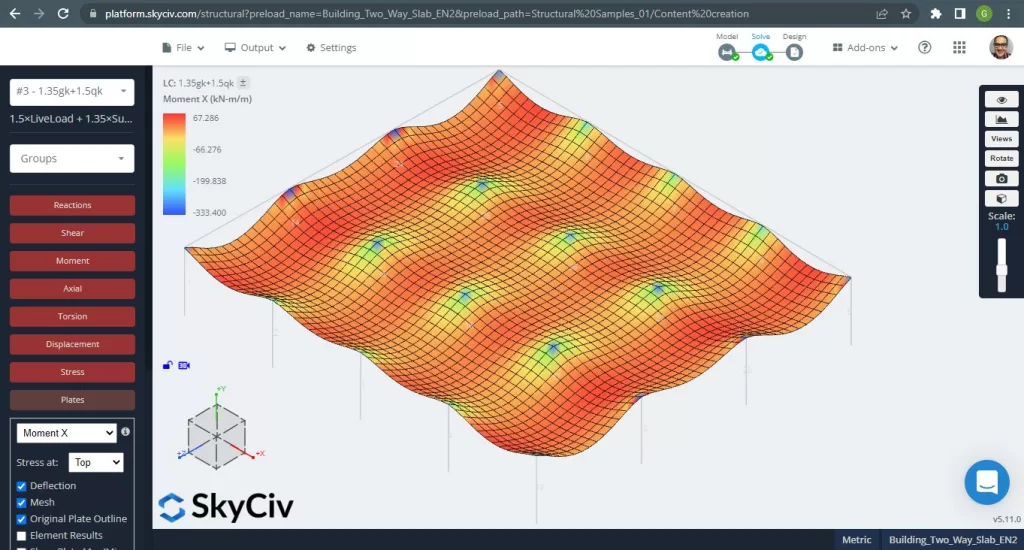
Φιγούρα 15. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
εικόνες 15 και 16 αποτελούνται από τη ροπή κάμψης σε κάθε κύρια κατεύθυνση. Λαμβάνοντας την κατανομή της στιγμής και τις τιμές, το λογισμικό, SkyCiv, μπορεί να αποκτήσει τότε τη συνολική επιφάνεια οπλισμού χάλυβα.

Φιγούρα 16. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
Χώροι ενίσχυσης από χάλυβα:
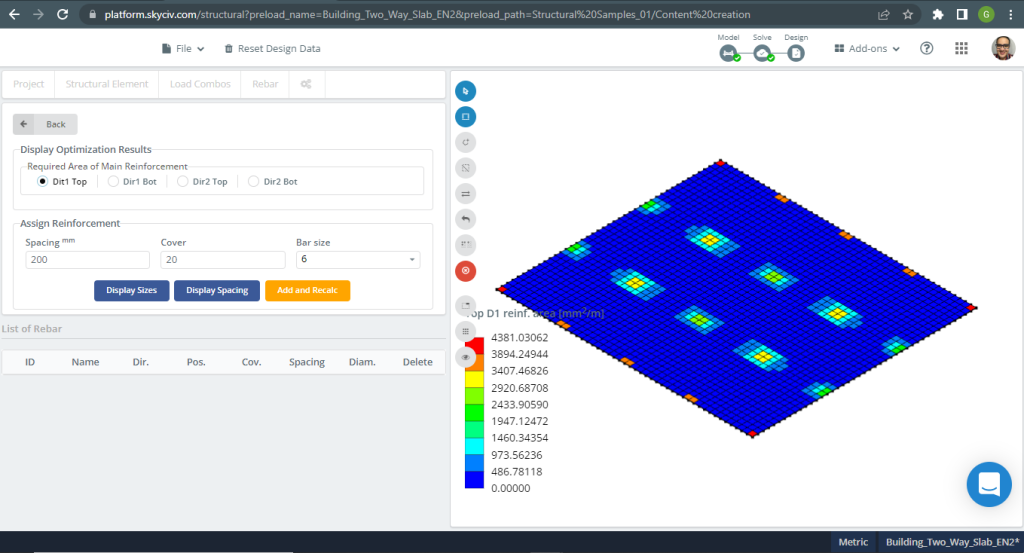
Φιγούρα 17. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
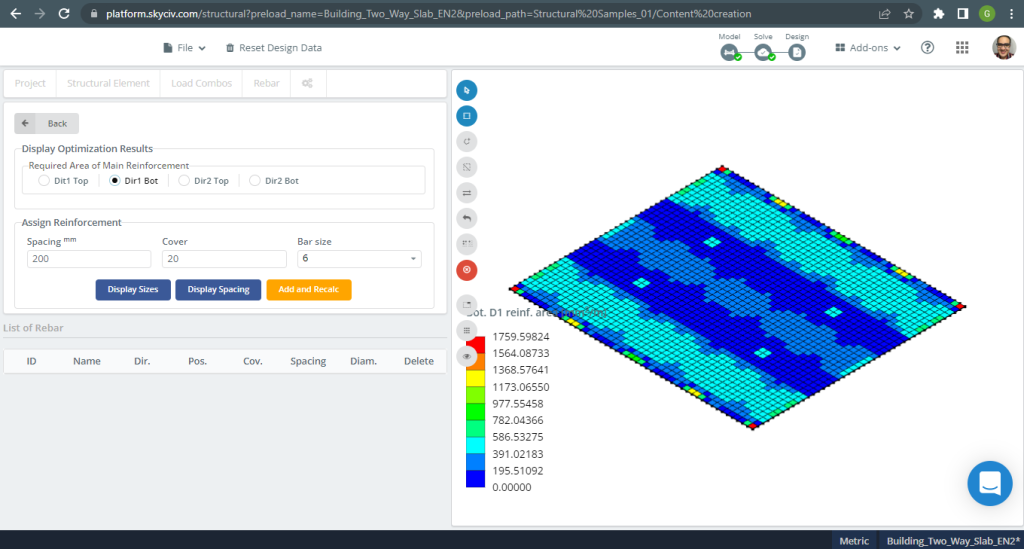
Φιγούρα 18. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
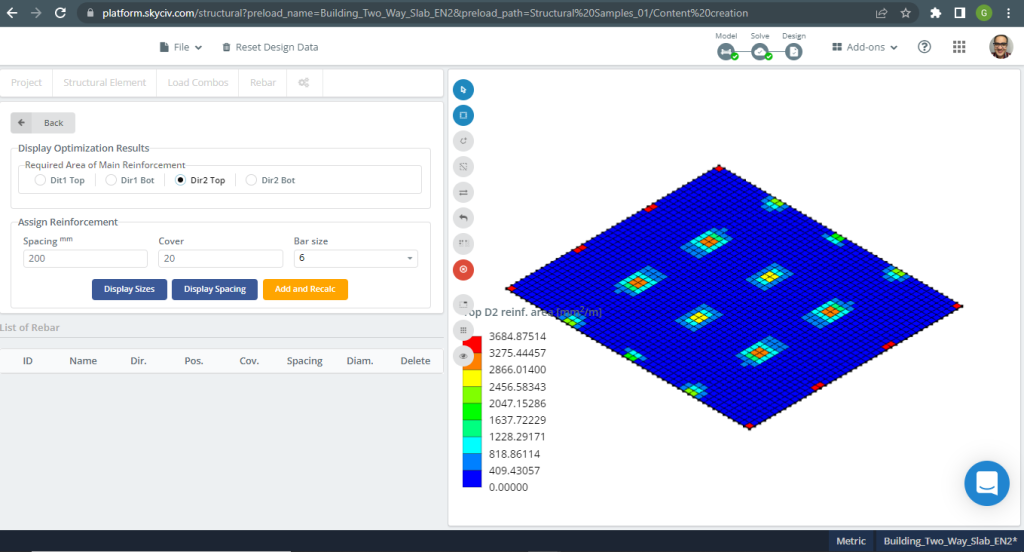
Φιγούρα 19. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
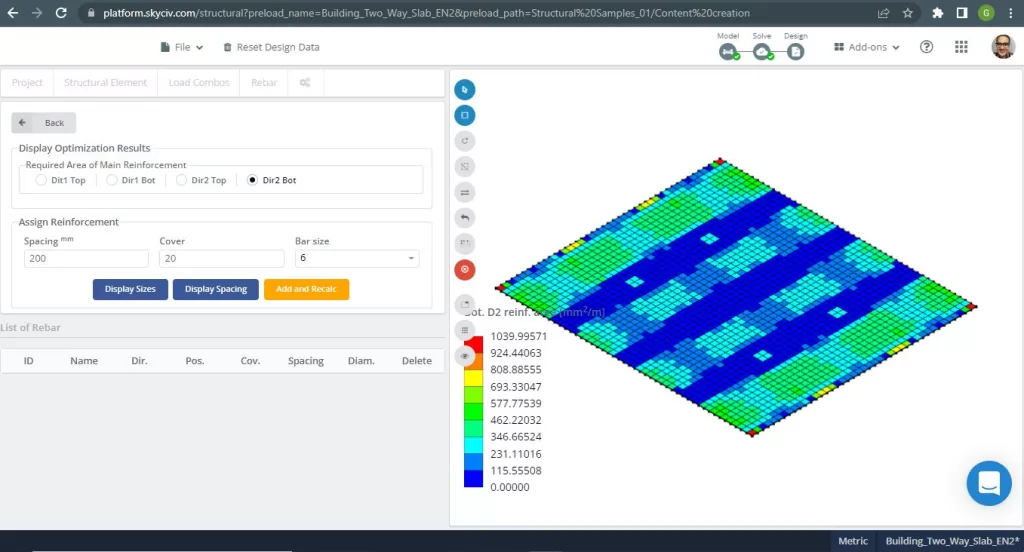
Φιγούρα 20. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
Σύγκριση αποτελεσμάτων
Το τελευταίο βήμα σε αυτό το παράδειγμα αμφίδρομης σχεδίασης πλάκας είναι η σύγκριση της επιφάνειας του χαλύβδινου οπλισμού που λαμβάνεται με ανάλυση S3D και υπολογισμούς με το χέρι.
Χάλυβας οπλισμού για κατεύθυνση Χ και λωρίδα στήλης
| Στιγμές και περιοχή χάλυβα | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| \(ΕΝΑ_{αγ, HandCalcs} {mm^2}\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
| \(ΕΝΑ_{αγ, S3D} {mm^2}\) | 3889.375 | 1040.00 | 4196.145 | 4196.145 | 520.00 | 3175.00 |
| \(\Δέλτα_{διαφ}\) (%) | 61.475 | 37.04 | 46.44 | 38.566 | 68.52 | 40.544 |
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
βιβλιογραφικές αναφορές
- σι. Mosley, Ρ. Hulse, J.H. Bungey , “Σχεδιασμός Οπλισμένου Σκυροδέματος σύμφωνα με τον Ευρωκώδικα 2”, Έβδομη έκδοση, Πάλγκρειβ ΜακΜίλαν.
- Μπαζάν Ενρίκε & Μελί Πιράλλα, “Σεισμική Μελέτη Κατασκευών”, 1εκδ, ΣΑΦΗ.
- Ευρωκώδικας 2: Σχεδιασμός κατασκευών από σκυρόδεμα.


