Σε αυτό το άρθρο, θα αναπτύξουμε ένα παράδειγμα σχεδίασης πλακών χρησιμοποιώντας την τελευταία έκδοση του ACI-318-19: “Απαιτήσεις κωδικού δόμησης για δομικό σκυρόδεμα,” που αποτελείται από τη μοντελοποίηση στο SkyCiv ενός κτιρίου από οπλισμένο σκυρόδεμα χαμηλής οροφής που επικεντρώνεται στη σύγκριση των αποτελεσμάτων λογισμικού και των υπολογισμών με το χέρι με μια αποδεκτή μέθοδο από την ACI: “Η Μέθοδος Άμεσης Σχεδιασμού για Πλάκες.” Αυτή η διαδικασία συνίσταται στην αντιστοίχιση σε διαφορετικές λωρίδες κατά μήκος των κύριων κατευθύνσεων και πλαισίων του κτιρίου της συνολικής ροπής με κατάλληλους παράγοντες για τον προσδιορισμό της ποσότητας του οπλισμού και της θέσης στην πλάκα..

Ελπίζουμε να έχετε διαβάσει το προηγούμενο άρθρο, Σχεδιασμός πιάτων σε S3D, για να μυηθείτε στη μοντελοποίηση και τη σχεδίαση πιάτων χρησιμοποιώντας το SkyCiv. Μια άλλη χρήσιμη πληροφορία που προτείνουμε να εξετάσετε βρίσκεται σε Πώς να μοντελοποιήσετε πιάτα? Μόλις ολοκληρώσετε την ανάγνωση και των δύο εγγράφων, μη διστάσετε να βουτήξετε στο ακόλουθο πλήρες παράδειγμα σύγκρισης πλακών!

Γενική Διάταξη Κτιρίου

Οι παρακάτω εικόνες δείχνουν μια ισομετρική όψη και διαστάσεις κάτοψης του προς υπολογισμό παραδείγματος. Το κτίριο έχει δύο υπερυψωμένες επίπεδες πλάκες χωρίς δοκούς μεταξύ των στηρίξεων κιόνων.

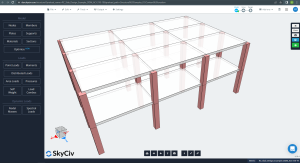
Φιγούρα 1. Ισομετρική άποψη του κτιρίου παράδειγμα

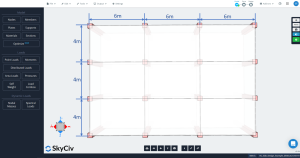
Φιγούρα 2. Διαστάσεις κάτοψης πλάκας

Μέθοδος Άμεσης Σχεδιασμού για Πλάκες Διόδων (DDM)

Περιορισμοί

ACI 318 επιτρέπει τη χρήση του DDM για το σχεδιασμό πλακών από οπλισμένο σκυρόδεμα για φορτία βαρύτητας, που συγκεντρώνουν κάποια προαπαιτούμενα ανάλογα με τη γεωμετρία, σχέσεις φορτίου, συμμετρία, και τα λοιπά. Μπορούμε να συνοψίσουμε αυτούς τους περιορισμούς στην παρακάτω λίστα (Σημειώσεις PCA):

• “Πρέπει να υπάρχουν τρία ή περισσότερα συνεχόμενα ανοίγματα σε κάθε κατεύθυνση.”: Φιγούρα 2 δείχνει τρία ανοίγματα σε κάθε κύρια κατεύθυνση, διαμήκης και εγκάρσια. Εντάξει!
• “Οι πλάκες πρέπει να είναι ορθογώνιες με αναλογία μεγαλύτερο προς μικρότερο άνοιγμα (κεντρική προς κεντρική γραμμή στηρίξεων) όχι μεγαλύτερο από 2.”: Σύμφωνα με το σχήμα 2, η αναλογία είναι ίση με \({\frac{l_1}{4}= frac{6Μ}{4Μ}=1,5 < 2}\). Εντάξει!
• “Διαδοχικά μήκη ανοιγμάτων (κεντρική προς κεντρική γραμμή στηρίξεων) σε κάθε κατεύθυνση δεν πρέπει να διαφέρει περισσότερο από 1/3 του μεγαλύτερου διαστήματος”. Τα μήκη των ανοιγμάτων είναι τα ίδια σε κάθε κατεύθυνση, 6m στο διαμήκη και 4m στο εγκάρσιο. Εντάξει!
• “Οι στήλες δεν πρέπει να μετατοπίζονται περισσότερο από 10% του εύρους (προς την κατεύθυνση της μετατόπισης) από κάθε άξονα μεταξύ κεντρικών γραμμών διαδοχικών στηλών”. Το παράδειγμα κτιρίου δεν έχει μετατοπίσεις στις στήλες. Εντάξει!
• “Τα φορτία πρέπει να κατανέμονται ομοιόμορφα, με το μη παραγοντωτό ή το ενεργό φορτίο υπηρεσίας όχι περισσότερο από δύο φορές το μη παραγοντωτό ή το νεκρό φορτίο υπηρεσίας (L/D ≤ 2)”. Λαμβάνοντας τις τιμές κάθε φορτίου βαρύτητας, η αναλογία ορίζεται ως \({\frac{μεγάλο}{ρε}= frac{2}{7.8}=0,256 < 2}\). Εντάξει!.
• “Για πλάκες διπλής κατεύθυνσης με δοκό, Η σχετική ακαμψία των δοκών σε δύο κάθετες κατευθύνσεις πρέπει να ικανοποιεί τις ελάχιστες και μέγιστες απαιτήσεις που αναφέρονται στον κώδικα.” Ήδη ικανοποιημένος; δεν υπάρχουν δοκοί στις πλάκες. Εντάξει!
• “Δεν επιτρέπεται η ανακατανομή αρνητικών στιγμών με κωδικό.” Λόγω της απλότητας του παραδείγματος, δεν θα είναι απαραίτητο να ανακατανεμηθούν οι αρνητικές ροπές στις πλάκες. Εντάξει!.

Ορισμός διαμήκων και εγκάρσιων λωρίδων

Η πλάκα στο DDM πρέπει να χωριστεί σε δύο κύριες λωρίδες για την ανάλυση και το σχεδιασμό ενός συγκεκριμένου πλέγματος γραμμής: στήλη και μεσαίες λωρίδες. Το πλάτος για τις λωρίδες στηλών είναι το μικρότερο \({\frac {l_1}{4}}\) και \({\frac{l_2}{4}}\), όπου \({l_1}\) είναι το μήκος του ανοίγματος κατά μήκος του πλέγματος γραμμής και \({l_2}\) είναι το εγκάρσιο μήκος κάθετο.

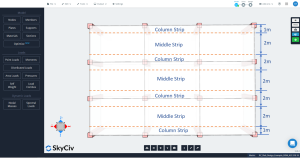
Φιγούρα 3. Διαμήκης στήλη και μεσαίες λωρίδες.

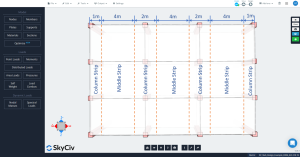
Φιγούρα 4. Εγκάρσια στήλη και μεσαίες λωρίδες.

Ελάχιστο πάχος

Το ACI-318 προτείνει τη χρήση της εξίσωσης: \({αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ελάχ}}= {\frac{l_n}{30}}={\frac{6Μ-0.50Μ}{30}}=0,1833m = 0,20m)

Προκαταρκτικός έλεγχος διατμητικής αντοχής

Πριν τον υπολογισμό του οπλισμού οπλισμού από χάλυβα, Συνιστάται ο έλεγχος της διατμητικής ικανότητας της πλάκας, το ένα για την άμεση διάτμηση στη σύνδεση και το άλλο για τη διατμητική ικανότητα διάτρησης στην κολόνα της πλάκας σύνδεσης.

Για τον υπολογισμό της ζήτησης διάτμησης, χρησιμοποιούμε τα ακόλουθα φορτία βαρύτητας:

• Πλάκα αυτο-βάρους: \({ΝΔ={\gamma_c}\φορές {αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{πλάκα}}={24 {\frac{ΚΝ}{m^3}}}\φορές {0.20Μ}=4,8{\frac{ΚΝ}{m^2}} }\)
• Υπερτιθέμενο νεκρό φορτίο: \({SD={3 {\frac{ΚΝ}{m^2}}}}\)
• Συνολικό νεκρό φορτίο (SW+SD): \({D={7.8 {\frac{ΚΝ}{m^2}}}}\)
• Ζωντανό φορτίο (Κατοικία κατοικίας) : \({L={2 {\frac{ΚΝ}{m^2}}}}\)
• Συντελεστικό φορτίο αντοχής (1.2D+1,6L): \({q_{εσύ}={12.56 {\frac{ΚΝ}{m^2}}}}\)

Ο πρώτος έλεγχος διάτμησης είναι ο “δοκός-διάτμηση” τύπος, όπου η παρακάτω εικόνα δείχνει την περιοχή που πρέπει να ληφθεί υπόψη για να ληφθεί η συνολική διάτμηση. Επιθεωρούμε κάθε κατεύθυνση, λαμβάνοντας την πιο εκτεταμένη περιοχή.

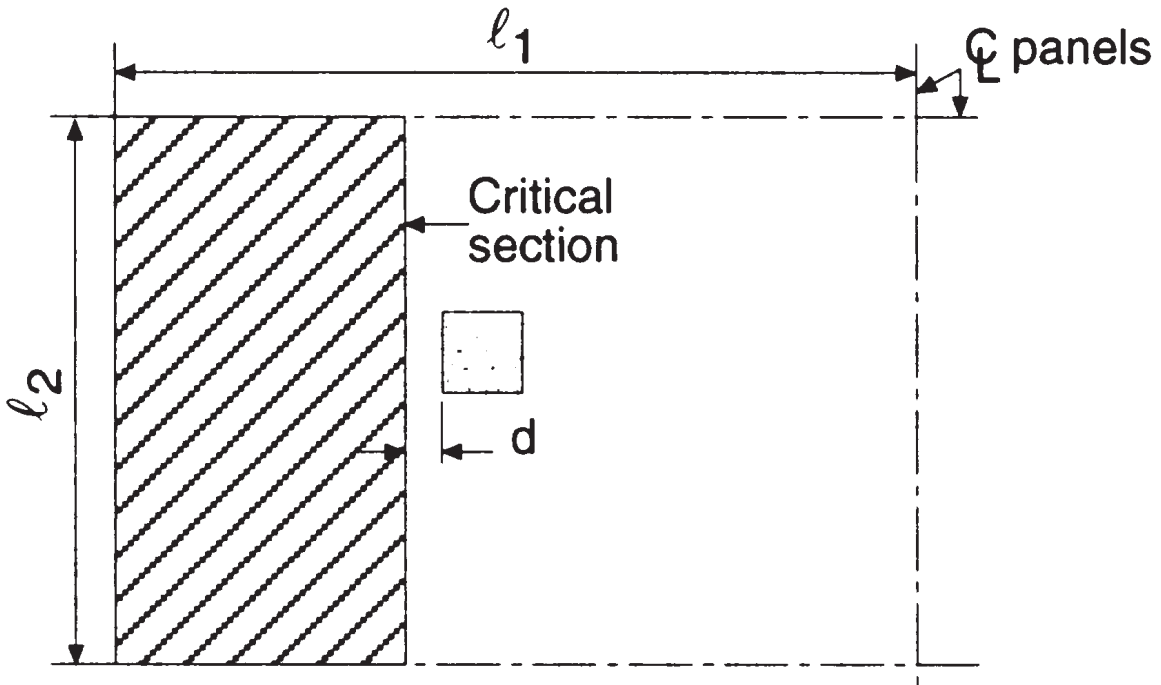
Φιγούρα 5. Διάτμηση δοκού στην εσωτερική στήλη (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

Οπου:

• Μήκος άνοιγμα κατά τη διαμήκη διεύθυνση, \({l_1 = 6,0μ }\)
• Μήκος άνοιγμα σε εγκάρσια διεύθυνση, \({l_2 = 4,0μ}\)
• Συνολική έκταση παραπόταμου, διάτμηση κατά τη διαμήκη διεύθυνση \({A_t = l_2 φορές (\frac{l_1}{2}-\frac{c_1}{2}-ρε) = 4,0 m φορές (\frac{6.0Μ}{2}-\frac{0.50Μ}{2}-0.17Μ) = 10.32 m^2}\) (επιλεγμένο)
• Συνολική έκταση παραπόταμου, διάτμηση σε εγκάρσια διεύθυνση, \({A_t = l_1 φορές (\frac{l_2}{2}-\frac{c_2}{2}-ρε) = 6,0 m φορές (\frac{4.0Μ}{2}-\frac{0.50Μ}{2}-0.17Μ) = 9.48 m^2}\)
• Διάσταση τετράγωνων στηλών, \({c_1 = c_2 = 0,50μ}\)
• Απόσταση δ, \({d = h_{πλάκα} – κάλυμμα = 0,20μ – 0.03m = 0,17m }\)

Επομένως, η μέγιστη διάτμηση δοκού στην εσωτερική στήλη είναι

\({V_u =q_u φορές A_t =12,56 {\frac{ΚΝ}{m^2}}\φορές 10.32 m^2 = 129.62 ΚΝ }\)

Αυτό θα συγκριθεί με την αντίσταση διάτμησης, \({\phi_sV_c}\)

• Αντοχή σκυροδέματος, \({f’_c = 25 MPa}\)
• Αντοχή χάλυβα οπλισμού, \({f_y = 420 MPa}\)
• \({\φι_ς = 0.75}\)
• \({\phi_sV_c = 0,17phi_s lambda sqrt(f'_c) b_w d; b_w=l_2}\)

\({\phi_sV_c = 0,17 φορές 0,75 φορές 1 φορές sqrt(25 MPa) \φορές 4000 mm φορές 170 mm = 433.50 ΚΝ }\)

Μπορούμε να δούμε ότι η διατμητική αντίσταση είναι μεγαλύτερη από τη ζήτηση διάτμησης: \({\phi_sV_c = 433.50 ΚΝ > V_u = 129.62 ΚΝ }\) Εντάξει!.

Σύμφωνα με τις παρακάτω εικόνες, πρέπει να υπολογίσουμε τη διατμητική ικανότητα διάτρησης και τη δύναμη που πρέπει να αντισταθεί από το σκυρόδεμα στην εσωτερική σύνδεση πλάκας-κολώνας. Η πρόθεση του κώδικα για τον έλεγχο της διάτμησης διάτρησης είναι να διατηρεί χαμηλές τιμές διατμητικής τάσης.

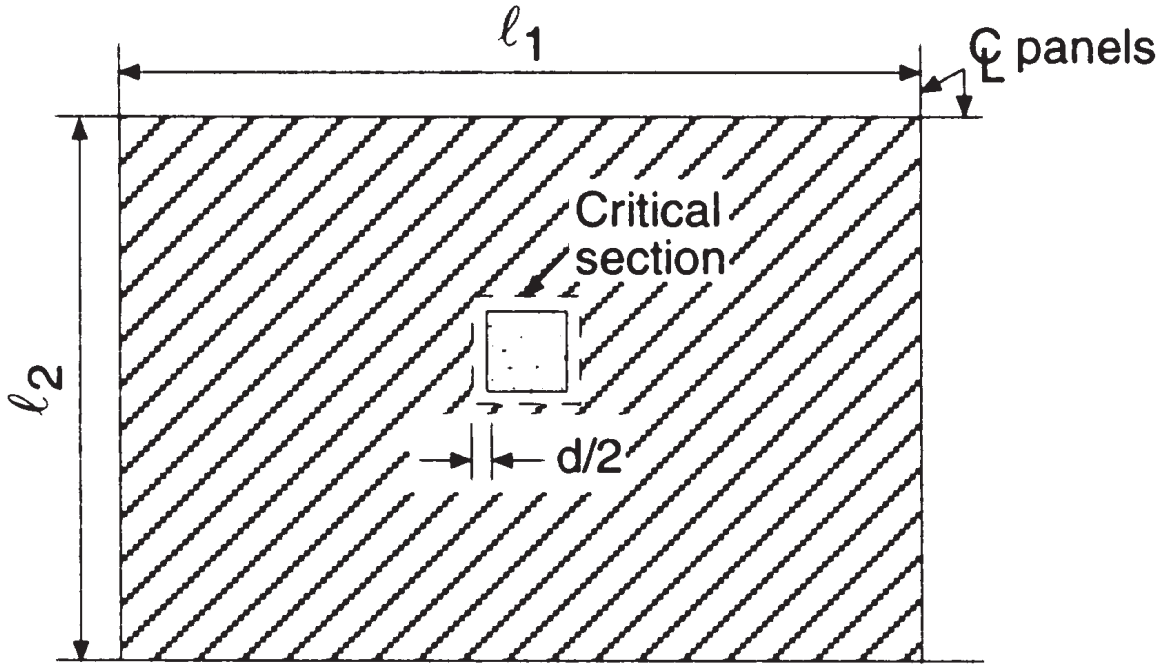
Φιγούρα 6. Αμφίδρομη διάτμηση στην εσωτερική κολόνα (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

• Συνολική έκταση παραπόταμου, διάτμηση διάτμησης, \({A_t = l_1 φορές l_2 – (c_1+d)^2 = 6,0 m φορές 4,0 m – (0.50μ+0,17μ)💕⬛ Αγορά Indocin από 23.55 m^2}\) (ίδια περιοχή και για τις δύο κύριες κατευθύνσεις)

Η συνολική δύναμη διάτμησης που πρέπει να αντισταθεί είναι

\({V_u =q_u φορές A_t =12,56 {\frac{ΚΝ}{m^2}}\φορές 23.55 m^2 = 295.79 ΚΝ }\)

Για να αποκτήσετε τη διατμητική ικανότητα διάτρησης σε μια πλάκα διπλής κατεύθυνσης, θα χρησιμοποιήσουμε την εμπειρική μέθοδο που καθιερώθηκε από τον κωδικό ACI-318, που λαμβάνει υπόψη τη μέγιστη διατμητική τάση που είναι διαθέσιμη στην ενεργή περίμετρο στο κρίσιμο τμήμα. Η πιο συντηρητική έκφραση για την εσωτερική στήλη είναι

• Διατμητική ικανότητα διάτρησης, \({\phi_sV_c = 0,33phi_s lambda sqrt(f'_c) b_0 d; b_0=4φορές (c_1+d)}\)

Επομένως, έχουμε τη διατμητική αντίσταση του

\({\phi_sV_c = 0,33 φορές 0.75 \φορές 1 \τ.μ.(25 MPa) \φορές (4\φορές (500 mm+170 mm)\φορές 170 χλστ) = 563.81 ΚΝ }\)

Μπορούμε να δούμε ότι η διατμητική αντίσταση είναι μεγαλύτερη από τη ζήτηση διάτμησης: \({\phi_sV_c = 563.81 ΚΝ > V_u = 295.75 ΚΝ }\) Εντάξει!.

Επαληθεύσαμε τις απαιτήσεις μονής και αμφίδρομης διάτμησης στη σύνδεση του εσωτερικού υποστυλώματος. Επειδή και οι δύο απαιτήσεις είναι μικρότερες από τις αντίστοιχες ικανότητες ή αντιστάσεις τους, θα προχωρήσουμε τώρα στον υπολογισμό του κύριου οπλισμού οπλισμού για την κάμψη της πλάκας.

Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!

Εγγραφείτε στο SkyCiv!

Συνολική συντελεστή στατικής ροπής ανά εύρος.

Η μέγιστη ροπή που μπορεί να αναπτυχθεί σε διπλή δέσμη σταθερού άκρου είναι μια ισοστατική ροπή ίση με \({Μ = frac{w φορές {l_1}^ 2}{8}}\) (Δείτε το σχήμα 6).

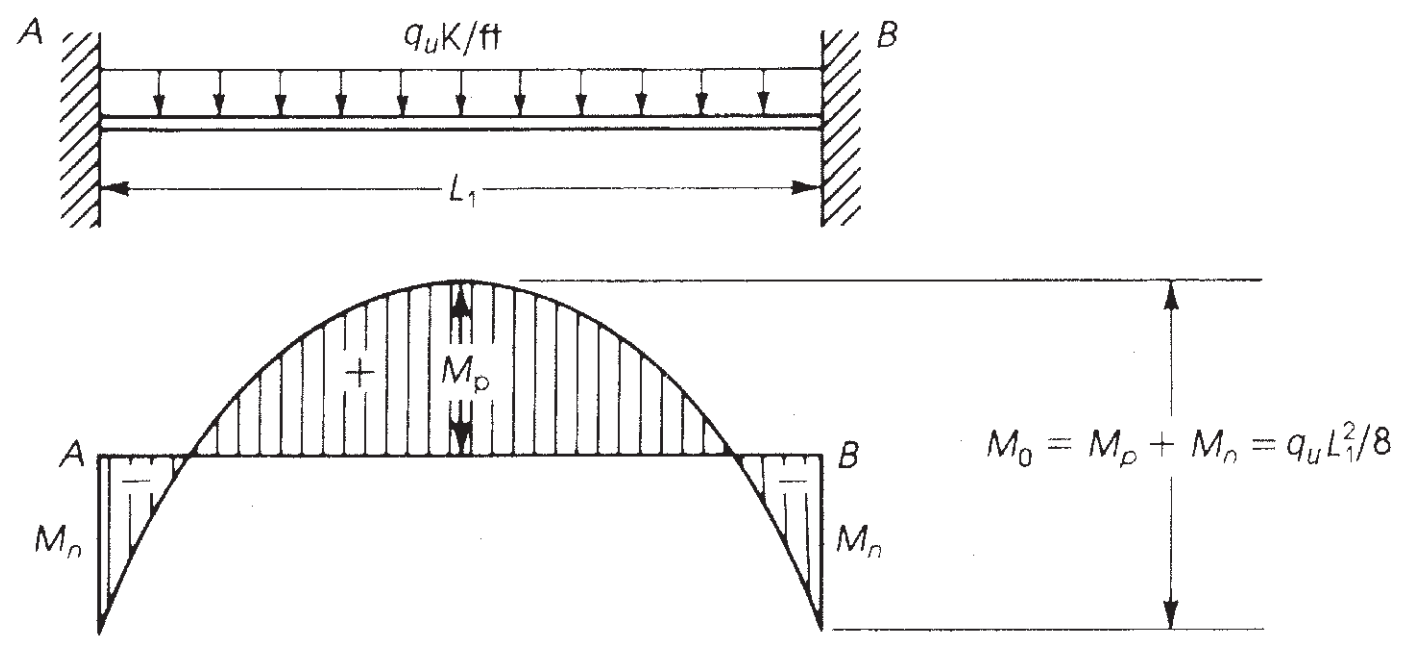
Φιγούρα 7. Ροπή κάμψης σε δοκό σταθερού άκρου. (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

Το ACI-18 παίρνει αυτή την αρχή και, για τη Μέθοδο Άμεσης Σχεδίασης (DDM), καθορίζει τη μέγιστη στατική ροπή που πρέπει να λαμβάνεται υπόψη ανά άνοιγμα \({M_0}\)

Διαμήκης κατεύθυνση:

• \({M_0 = frac {q_u φορές l_2 φορές {μεγάλο_{ν,1}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{ΚΝ}{m^2}}\φορές 4,0 mφορές (6Μ-0.50Μ)^ 2}{8}=189,97 kN-m}\)

Εγκάρσια κατεύθυνση:

• \({M_0 = frac {q_u φορές l_1 φορές {μεγάλο_{ν,2}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{ΚΝ}{m^2}}\φορές 6,0 mφορές (4Μ-0.50Μ)^ 2}{8}=115,40 kN-m}\)

Το επόμενο βήμα είναι να αντιστοιχίσετε αυτή τη συνολική ροπή λαμβάνοντας υπόψη τον τύπο του πίνακα, εσωτερικό ή εξωτερικό. (Δείτε το σχήμα 7). Μετά από αυτό, λόγω του συνεχούς ανοίγματος, είναι απαραίτητο να χωρίσουμε επίσης τη στιγμή σε θετική και αρνητική. Αυτό το τελευταίο φαίνεται σε εικόνες 8 και 9.

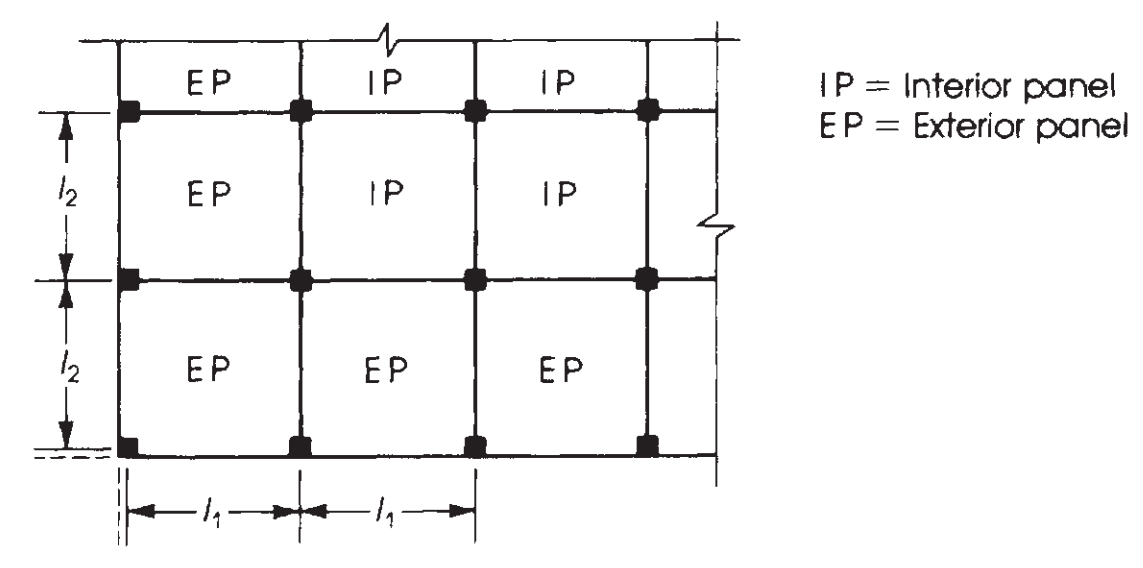
Φιγούρα 8. Ορισμός πάνελ σύμφωνα με τη σχετική θέση τους σε κάτοψη πλάκας. (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

 

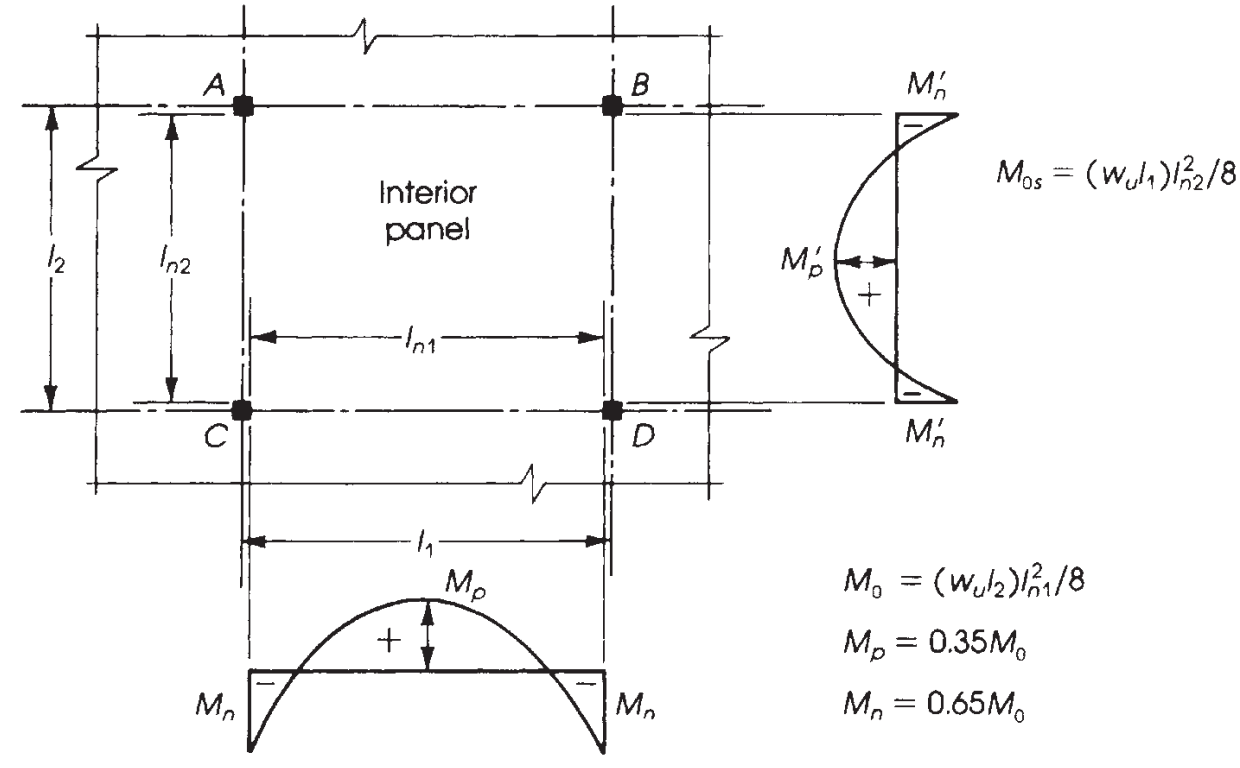
Φιγούρα 9. Κατανομή ροπών σε εσωτερικό πάνελ. (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

 

Είναι κρίσιμο να γνωρίζουμε τη σωστή κατανομή των ροπών ανάλογα με την πλάκα που σχεδιάζουμε. Σε αυτό το παράδειγμα, έχουμε την τελευταία περίπτωση στην παρακάτω εικόνα (φιγούρα 9), “Χωρίς δοκάρια,” εφαρμόζεται σε επίπεδη πλάκα ή συμπαγή πλάκα χωρίς δοκό, ούτε στην άκρη ούτε ανάμεσα στα στηρίγματα.

Η κύρια διαφορά στις πέντε περιπτώσεις που φαίνεται στο σχήμα 9 είναι τα κλάσματα ροπής που πρέπει να αντιστοιχιστούν σε εξωτερικά πάνελ, στην οποία ο σχετικός περιορισμός στο τέλος αλλάζει τις προς υπολογισμό τιμές.

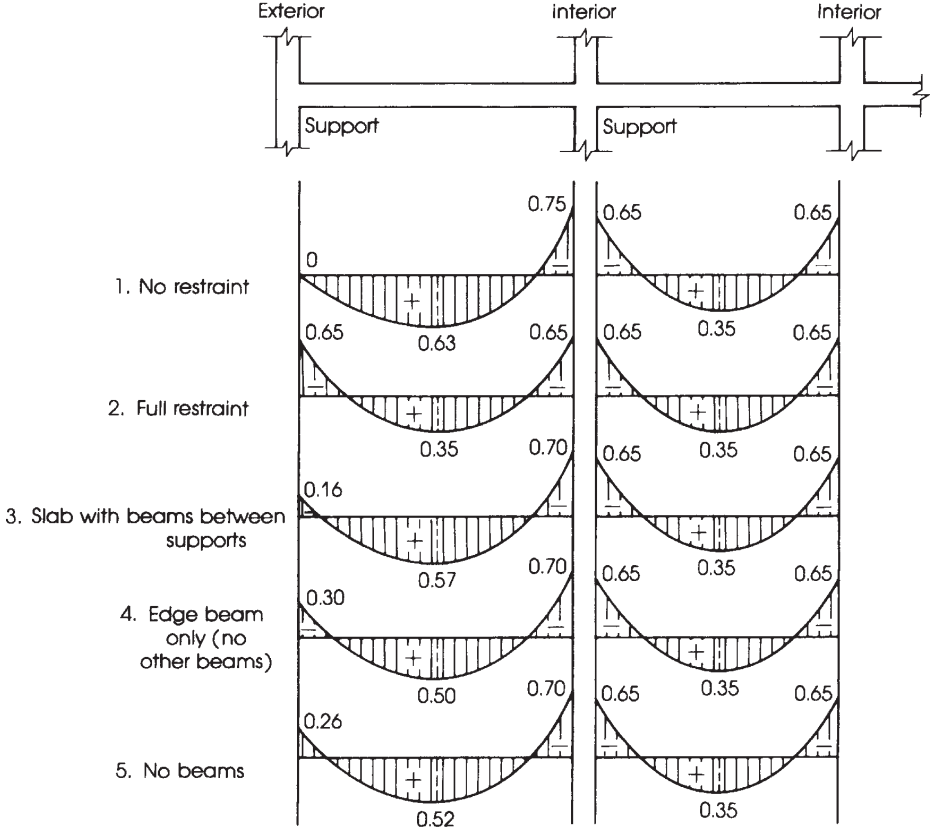
Φιγούρα 10. Κατανομή της συνολικής στατικής ροπής σε ροπές αρνητικού και θετικού διαστήματος. (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

Κατανομή της συνολικής συντελεστής ροπής \({M_0}\) ανά διάστημα σε αρνητικές και θετικές στιγμές.

Μια φορά \({M_0}\) έχει υπολογιστεί, είναι καιρός να αντιστοιχίσετε το κλάσμα των ροπών σε θετικές και αρνητικές σε κάθε λωρίδα σχεδίασης, αυτό είναι, στήλη και μεσαίες λωρίδες. Για περισσότερη σαφήνεια, φιγούρα 10 βοηθά στον καθορισμό του κατάλληλου παράγοντα που πρέπει να ληφθεί υπόψη στην κατανομή της συνολικής ροπής.

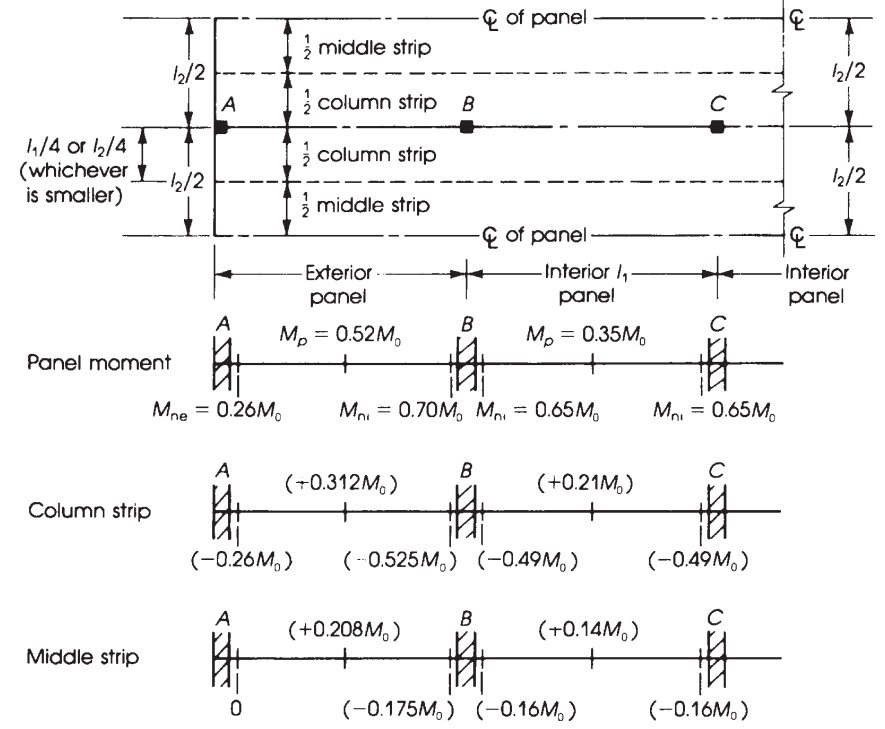
Φιγούρα 11. Πλάτος του ισοδύναμου άκαμπτου πλαισίου και κατανομή των ροπών σε επίπεδες πλάκες. (Nadim Hassoun και Akthem AI-Manaseer, “Βιβλίο RC”)

Χρησιμοποιώντας τους προηγούμενους παράγοντες που υποδεικνύονται στο σχήμα 10, παίρνουμε στον παρακάτω πίνακα την τελική στιγμή.

Διαμήκης κατεύθυνση: \({M_0 = 189.97 kN-m}\)

Σπιθαμή (ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Συνολική στιγμή (kN-m)	Ροπή λωρίδας στήλης (kN-m)	Στιγμή μεσαίας λωρίδας (kN-m)
Εξωτερικό Αρνητικό ES	0.26Μ0=49,39	0.26Μ0=49,39	0
Θετικό ΕΣ	0.52Μ0=98,78	0.31Μ0=58,89	0.21Μ0=39,89
Εσωτερικό Αρνητικό ES	0.70Μ0=132,98	0.53Μ0=100,68	0.17Μ0=32,29
Θετικό ΕΙΝΑΙ	0.35Μ0=66,49	0.21Μ0=39,89	0.14Μ0=26,60
Αρνητικό IS	0.65Μ0=123,48	0.49Μ0=93,09	0.16Μ0=30,40

Με τη στιγμή που διανεμήθηκε κάποτε, είναι καιρός να προσδιοριστεί ο οπλισμός οπλισμού από χάλυβα που θα τοποθετηθεί στην πλάκα. Θα αναπτύξουμε μόνο έναν υπολογισμό και στη συνέχεια όλα τα αποτελέσματα σε έναν πίνακα.

Ροπή στο εξωτερικό αρνητικό άνοιγμα στη λωρίδα στήλης, \({M_u = 49.39 kN-m}\)

• Υποτιθέμενο τμήμα ελεγχόμενης τάσης. \({\φι_φ = 0.9}\)
• Πλάτος λωρίδας στήλης, \({β=2,0μ}\)
• Χώρος ενίσχυσης από χάλυβα, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{49.39kN-m}{0.9\φορές 0.9(0.17Μ)\φορές 420 MPa}=853.996 {χιλ}^ 2}\)
• \({\Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα{ελάχ} = 0.0018}\). Ελάχιστη περιοχή ενίσχυσης από χάλυβα, \({ΕΝΑ_{μικρό,ελάχ}=rho_{ελάχ}\φορές b φορές d = 0.0018 \φορές 2,0m φορές 0,17m =612 {χιλ}^ 2}\). Τώρα, ελέγξτε εάν το τμήμα συμπεριφέρεται ως ελεγχόμενη από την τάση.
• \({a = frac{A_s φορές f_y}{0.85\φορές f’c φορές β} = frac{853.996 {χιλ}^ 2 φορές 420 MPa}{0.85\φορές 25 MPa φορές 2,0μ }= 8.439 χιλ}\)
• \({c = frac{ένα}{\βήτα_1}= frac{8.439 χιλ}{0.85} = 9,929 χλστ }\)
• \({\varepsilon_t = (\frac{0.003}{ντο})\φορές d – 0.003 = (\frac{0.003}{9.929χιλ})\φορές 170 χλστ – 0.003 = 0.048 > 0.005 }\) Εντάξει!, είναι ένα τμήμα ελεγχόμενης έντασης!.

Σπιθαμή(ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Στιγμή λωρίδας στήλης (kN-m)	\({ΕΝΑ_{μικρό,υπολ} ({χιλ}^ 2)}\)	\({ΕΝΑ_{μικρό,ελάχ} ({χιλ}^ 2)}\)	\({ένα (χιλ)}\)	\({ντο (χιλ)}\)	\({\varepsilon_t > 0.005}\)
Εξωτερικό Αρνητικό ES	49.39	853.996	612.0	8.439	9.929	0.048 > 0.005!
Θετικό ΕΣ	58.89	1018.259	612.0	10.063	11.839	0.040 > 0.005!
Εσωτερικό Αρνητικό ES	100.68	1740.844	612.0	17.204	20.24	0.022 > 0.005!
Θετικό ΕΙΝΑΙ	39.89	689.733	612.0	6.816	8.019	0.06 > 0.005!
Αρνητικό IS	93.09	1609.607	612.0	15.907	18.714	0.024 > 0.005!

Ροπή στο εξωτερικό θετικό άνοιγμα στη μεσαία λωρίδα, \({M_u = 39.89 kN-m}\)

• Υποτιθέμενο τμήμα ελεγχόμενης τάσης. \({\φι_φ = 0.9}\)
• Μεσαίο πλάτος λωρίδας, \({β=2,0μ}\)
• Χώρος ενίσχυσης από χάλυβα, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{39.89kN-m}{0.9\φορές 0.9(0.17Μ)\φορές 420 MPa}=689.733 {χιλ}^ 2}\)
• \({\Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα{ελάχ} = 0.0018}\). Ελάχιστη περιοχή ενίσχυσης από χάλυβα, \({ΕΝΑ_{μικρό,ελάχ}=rho_{ελάχ}\φορές b φορές d = 0.0018 \φορές 2,0m φορές 0,17m =612 {χιλ}^ 2}\). Τώρα, ελέγξτε εάν το τμήμα συμπεριφέρεται ως ελεγχόμενη από την τάση.
• \({a = frac{A_s φορές f_y}{0.85\φορές f’c φορές β} = frac{689.766 {χιλ}^ 2 φορές 420 MPa}{0.85\φορές 25 MPa φορές 2,0μ }= 6.816 χιλ}\)
• \({c = frac{ένα}{\βήτα_1}= frac{6.816 χιλ}{0.85} = 8.019 χιλ }\)
• \({\varepsilon_t = (\frac{0.003}{ντο})\φορές d – 0.003 = (\frac{0.003}{8.019χιλ})\φορές 170 χλστ – 0.003 = 0.0605 > 0.005 }\) Εντάξει!, είναι ένα τμήμα ελεγχόμενης έντασης!.

Σπιθαμή(ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Στιγμή μεσαίας λωρίδας (kN-m)	\({ΕΝΑ_{μικρό,υπολ} ({χιλ}^ 2)}\)	\({ΕΝΑ_{μικρό,ελάχ} ({χιλ}^ 2)}\)	\({ένα (χιλ)}\)	\({ντο (χιλ)}\)	\({\varepsilon_t > 0.005}\)
Εξωτερικό Αρνητικό ES	0	0.00	612.0	6.048	7.115	0.069 > 0.005!
Θετικό ΕΣ	39.89	689.733	612.0	6.816	8.019	0.061 > 0.005!
Εσωτερικό Αρνητικό ES	32.29	558.322	612.0	6.048	7.115	0.069 > 0.005!
Θετικό ΕΙΝΑΙ	26.60	459.937	612.0	6.048	7.115	0.069 > 0.005!
Αρνητικό IS	30.40	525.642	612.0	6.048	7.115	0.069 > 0.005!

Εγκάρσια κατεύθυνση: \({M_0 = 115.40 kN-m}\)

Σπιθαμή (ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Συνολική στιγμή (kN-m)	Ροπή λωρίδας στήλης (kN-m)	Στιγμή μεσαίας λωρίδας (kN-m)
Εξωτερικό Αρνητικό ES	0.26Μ0=30,00	0.26Μ0=30,00	0
Θετικό ΕΣ	0.52Μ0=60,00	0.31Μ0=35,77	0.21Μ0=24,23
Εσωτερικό Αρνητικό ES	0.70Μ0=80,78	0.53Μ0=61,16	0.17Μ0=19,62
Θετικό ΕΙΝΑΙ	0.35Μ0=40,39	0.21Μ0=24,23	0.14Μ0=16,16
Αρνητικό IS	0.65Μ0=75,01	0.49Μ0=56,55	0.16Μ0=18,46

Με τη στιγμή που διανεμήθηκε κάποτε, είναι καιρός να προσδιοριστεί ο οπλισμός οπλισμού από χάλυβα που θα τοποθετηθεί στην πλάκα. Θα αναπτύξουμε μόνο έναν υπολογισμό και στη συνέχεια όλα τα αποτελέσματα σε έναν πίνακα.

Ροπή στο εξωτερικό αρνητικό άνοιγμα στη λωρίδα στήλης, \({M_u = 30.00 kN-m}\)

• Υποτιθέμενο τμήμα ελεγχόμενης τάσης. \({\φι_φ = 0.9}\)
• Πλάτος λωρίδας στήλης, \({β=2,0μ}\)
• Χώρος ενίσχυσης από χάλυβα, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{30.00kN-m}{0.9\φορές 0.9(0.17Μ)\φορές 420 MPa}=518.726 {χιλ}^ 2}\)
• \({\Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα{ελάχ} = 0.0018}\). Ελάχιστη περιοχή ενίσχυσης από χάλυβα, \({ΕΝΑ_{μικρό,ελάχ}=rho_{ελάχ}\φορές b φορές d = 0.0018 \φορές 2,0m φορές 0,17m =612 {χιλ}^ 2}\). Τώρα, ελέγξτε εάν το τμήμα συμπεριφέρεται ως ελεγχόμενη από την τάση.
• \({a = frac{A_s φορές f_y}{0.85\φορές f’c φορές β} = frac{518.726 {χιλ}^ 2 φορές 420 MPa}{0.85\φορές 25 MPa φορές 2,0μ }= 6.048 χιλ}\)
• \({c = frac{ένα}{\βήτα_1}= frac{6.048 χιλ}{0.85} = 7.115 χλστ }\)
• \({\varepsilon_t = (\frac{0.003}{ντο})\φορές d – 0.003 = (\frac{0.003}{7.115χιλ})\φορές 170 χλστ – 0.003 = 0.069 > 0.005 }\) Εντάξει!, είναι ένα τμήμα ελεγχόμενης έντασης!.

Σπιθαμή(ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Στιγμή λωρίδας στήλης (kN-m)	\({ΕΝΑ_{μικρό,υπολ} ({χιλ}^ 2)}\)	\({ΕΝΑ_{μικρό,ελάχ} ({χιλ}^ 2)}\)	\({ένα (χιλ)}\)	\({ντο (χιλ)}\)	\({\varepsilon_t > 0.005}\)
Εξωτερικό Αρνητικό ES	30.00	518.726	612.0	6.048	7.115	0.069 > 0.005!
Θετικό ΕΣ	35.77	618.494	612.0	6.112	7.191	0.068 > 0.005!
Εσωτερικό Αρνητικό ES	61.16	1057.509	612.0	10.451	12.295	0.038 > 0.005!
Θετικό ΕΙΝΑΙ	24.23	418.958	612.0	6.048	7.115	0.069 > 0.005!
Αρνητικό IS	56.55	977.799	612.0	9.663	11.368	0.042 > 0.005!

Ροπή στο εξωτερικό θετικό άνοιγμα στη μεσαία λωρίδα, \({M_u = 24.23 kN-m}\)

• Υποτιθέμενο τμήμα ελεγχόμενης τάσης. \({\φι_φ = 0.9}\)
• Πλάτος λωρίδας στήλης, \({β=4,0μ}\)
• Χώρος ενίσχυσης από χάλυβα, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{24.23 kN-m}{0.9\φορές 0.9(0.17Μ)\φορές 420 MPa}=418.958 {χιλ}^ 2}\)
• \({\Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα{ελάχ} = 0.0018}\). Ελάχιστη περιοχή ενίσχυσης από χάλυβα, \({ΕΝΑ_{μικρό,ελάχ}=rho_{ελάχ}\φορές b φορές d = 0.0018 \φορές 4,0m φορές 0,17m =1224 {χιλ}^ 2}\). Τώρα, ελέγξτε εάν το τμήμα συμπεριφέρεται ως ελεγχόμενη από την τάση.
• \({a = frac{A_s φορές f_y}{0.85\φορές f’c φορές β} = frac{1224 {χιλ}^ 2 φορές 420 MPa}{0.85\φορές 25 MPa φορές 4,0μ }= 6.048 χιλ}\)
• \({c = frac{ένα}{\βήτα_1}= frac{6.048 χιλ}{0.85} = 7.115 χιλ }\)
• \({\varepsilon_t = (\frac{0.003}{ντο})\φορές d – 0.003 = (\frac{0.003}{7.115χιλ})\φορές 170 χλστ – 0.003 = 0.069 > 0.005 }\) Εντάξει!, είναι ένα τμήμα ελεγχόμενης έντασης!.

Σπιθαμή(ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Στιγμή μεσαίας λωρίδας (kN-m)	\({ΕΝΑ_{μικρό,υπολ} ({χιλ}^ 2)}\)	\({ΕΝΑ_{μικρό,ελάχ} ({χιλ}^ 2)}\)	\({ένα (χιλ)}\)	\({ντο (χιλ)}\)	\({\varepsilon_t > 0.005}\)
Εξωτερικό Αρνητικό ES	0.00	0.00	1224.00	6.048	7.115	0.069 > 0.005!
Θετικό ΕΣ	24.23	418.958	1224.00	6.048	7.115	0.069 > 0.005!
Εσωτερικό Αρνητικό ES	19.62	339.247	1224.00	6.048	7.115	0.069 > 0.005!
Θετικό ΕΙΝΑΙ	16.16	279.420	1224.00	6.048	7.115	0.069 > 0.005!
Αρνητικό IS	18.46	319.189	1224.00	6.048	7.115	0.069 > 0.005!

Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!

Εγγραφείτε στο SkyCiv!

Ενότητα σχεδίασης SkyCiv S3D

Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, περιγράφουμε το αποτέλεσμα σχεδίασης χρησιμοποιώντας τη μονάδα σχεδιασμού πιάτων που περιλαμβάνεται στο SkyCiv. Δεν εξηγούμε πώς να μοντελοποιήσουμε και να αναλύσουμε τη δομή (για αυτά, δείτε σχετικά άρθρα σχετικά με αυτό το θέμα στην τεκμηρίωσή μας: Πώς να μοντελοποιήσετε μια δομή στο SkyCiv?, Πώς να εφαρμόσω φορτία στο μοντέλο του κτιρίου μου? και Πώς να εκτελέσετε μια γραμμική ελαστική ανάλυση?)

Είναι βολικό να εφαρμόσετε ένα λεπτό πλέγμα στις πλάκες για να έχετε ένα ακριβές αποτέλεσμα σχεδιασμού. Ρίξτε μια ματιά στην παρακάτω εικόνα για περισσότερη σαφήνεια.

Φιγούρα 12. Λεπτότερο πλέγμα που εφαρμόζεται σε πλάκες

Το επόμενο βήμα είναι να εκτελέσετε τη μονάδα σχεδιασμού και να επιλέξετε τις επιλογές που υπολογίζουν μια βελτιστοποιημένη επιφάνεια οπλισμού από χάλυβα.

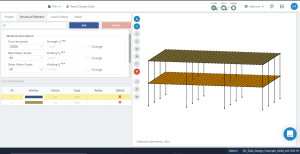
Φιγούρα 13. Ορισμός ιδιοτήτων πλάκας σκυροδέματος πριν από τη βελτιστοποίηση σχεδιασμού.

Φιγούρα 14 αντιπροσωπεύει τον τοπικό προσανατολισμό των αξόνων της πλάκας. Διότι τοπικός άξονας 3 είναι προς τα κάτω, ο “μπλουζα” είναι ο πάτος, και το “κάτω μέρος” θα είναι η κορυφή, λαμβάνοντας έτσι σωστά τα δεδομένα από το σχέδιο.

Ένα άλλο σημαντικό γεγονός είναι το μέγεθος του πλέγματος της πλάκας; είναι ένα τετράγωνο στοιχείο με κάτοψη 500mm x 500mm. Το SkyCiv S3D δίνει την περιοχή ενίσχυσης ως ενσωματωμένη τιμή ανά πεπερασμένο στοιχείο. Ετσι, εάν θέλουμε να λάβουμε το συνολικό εμβαδόν ράβδου οπλισμού μιας κολόνας ή μεσαίας λωρίδας, πρέπει να υπολογίσουμε τη μέση τιμή από τον αριθμό των στοιχείων που αθροίζουν το πλάτος της ταινίας που αναλύεται. Για παράδειγμα, για τη λωρίδα στήλης, θα εξεταστούν τέσσερα στοιχεία (4×0.5m = 2m).

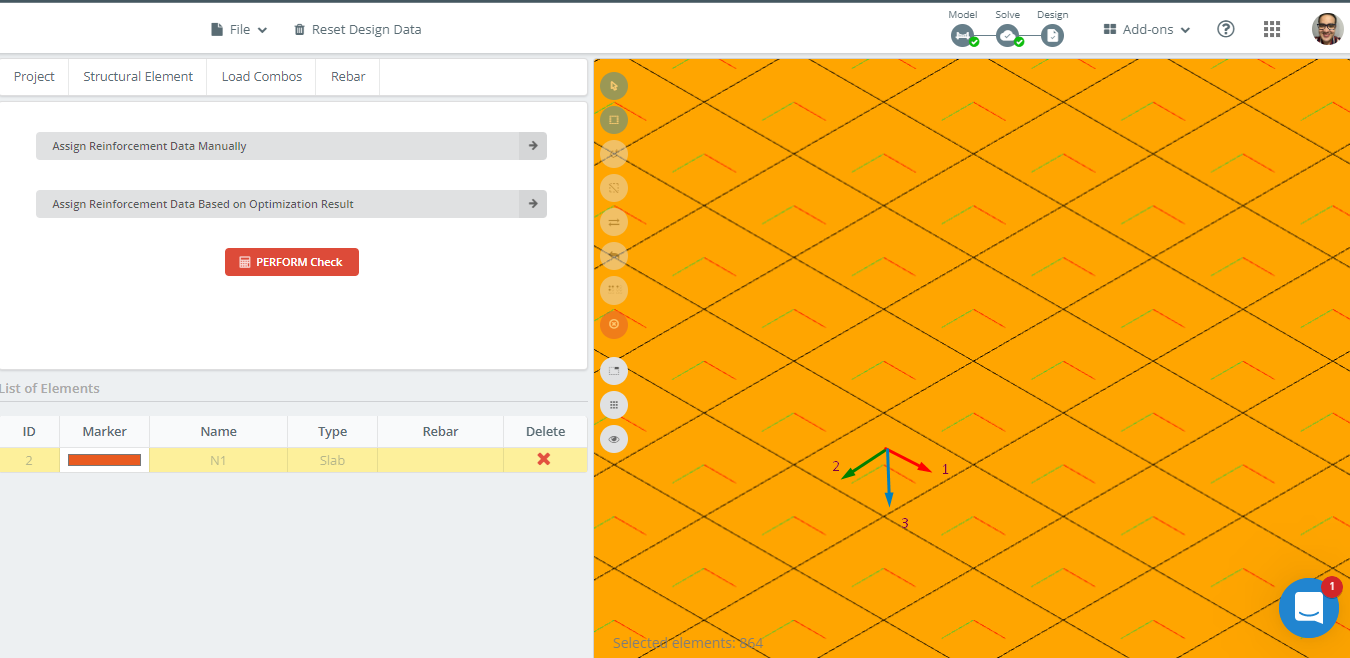
Φιγούρα 14. Τοπικός προσανατολισμός αξόνων σε παράδειγμα πλάκας.

Πρώτα, αναλύουμε την απαιτούμενη περιοχή οπλισμού κατά τη διαμήκη διεύθυνση στον άξονα 1.

Λωρίδα στήλης

• Εξωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(119.09\φορές 2 + 952.72 + 833.64 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 1012.27 {χιλ}^ 2}\)
• Εξωτερική θετική στιγμή (ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = 4*463.90 \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 927.80 {χιλ}^ 2}\)
• Εξωτερική εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(1071.82\φορές 2 +714.54 \φορές 2 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 1786.36 {χιλ}^ 2}\)
• Εσωτερική θετική στιγμή(ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = 4*309.27 \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 618.54 {χιλ}^ 2}\)
• Εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(714.54\φορές 2 +952.73 \φορές 2 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 1667.27 {χιλ}^ 2}\)

Μέση Λωρίδα

• Εξωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(119.09\φορές 4)\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 238.18 {χιλ}^ 2}\)
• Εξωτερική θετική στιγμή (ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = (463.90\φορές 2 +412.36 \φορές 2 ) \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 876.26 {χιλ}^ 2}\)
• Εξωτερική εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(357.27\φορές 2 +476.36 \φορές 2 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 833.63 {χιλ}^ 2}\)
• Εσωτερική θετική στιγμή(ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = 4*257.72 \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 515.44 {χιλ}^ 2}\)
• Εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(357.27\φορές 2 +476.36 \φορές 2 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 833.63 {χιλ}^ 2}\)

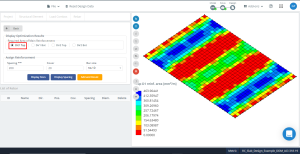
Φιγούρα 15. Η βελτιστοποίηση έχει ως αποτέλεσμα την κατεύθυνση “1” και την επάνω πλευρά (Κάτω πλευρά, πράγματι).

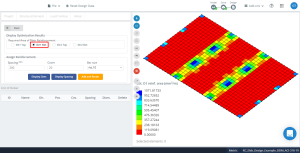
Φιγούρα 16. Η βελτιστοποίηση έχει ως αποτέλεσμα την κατεύθυνση “1” και την κάτω πλευρά (Πάνω πλευρά, πράγματι).

Τελικά, αναλύουμε την περιοχή οπλισμού που απαιτείται κατά μήκος της εγκάρσιας διεύθυνσης στον άξονα 2.

Λωρίδα στήλης

• Εξωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(91.55\φορές 2 + 457.73 + 549.28 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 595.055 {χιλ}^ 2}\)
• Εξωτερική θετική στιγμή (ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = (269.68\φορές 3+239.72) \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 524.38 {χιλ}^ 2}\)
• Εξωτερική εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(823.92\φορές 2 +549.28 +457.73)\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 1327.43 {χιλ}^ 2}\)
• Εσωτερική θετική στιγμή(ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = (179.79\φορές 3+149.82) \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 344.60 {χιλ}^ 2}\)
• Εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(823.92\φορές 2 +549.28 +457.73)\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 1327.43 {χιλ}^ 2}\)

Μέση Λωρίδα

• Εξωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(183.09\φορές 2+91,55φορές 6)\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 457.74 {χιλ}^ 2}\)
• Εξωτερική θετική στιγμή (ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = (209.75\φορές 2 +179.79 \φορές 2 +149.82 \φορές 4) \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 689.18{χιλ}^ 2}\)
• Εξωτερική εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(274.64\φορές 2+91,55φορές 6)\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 549.29 {χιλ}^ 2}\)
• Εσωτερική θετική στιγμή(ενίσχυση του πυθμένα): \({ΕΝΑ_{μικρό,bot} = (119.86\φορές 4 + 89.89\φορές 4) \frac{{χιλ}^ 2}{Μ}\φορές 0,50m = 419.50 {χιλ}^ 2}\)
• Εσωτερική αρνητική στιγμή (κορυφαία ενίσχυση): \({ΕΝΑ_{μικρό,μπλουζα} =(274.64\φορές 2+91,55φορές 6 )\frac{{χιλ}^ 2}{Μ} \φορές 0,50m = 549.29 {χιλ}^ 2}\)

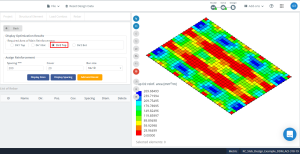
Φιγούρα 17. Η βελτιστοποίηση έχει ως αποτέλεσμα την κατεύθυνση “2” και την επάνω πλευρά (Κάτω πλευρά, πράγματι).

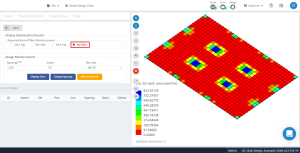
Φιγούρα 18. Η βελτιστοποίηση έχει ως αποτέλεσμα την κατεύθυνση “2” και την κάτω πλευρά (Πάνω πλευρά, πράγματι).

 

Σύγκριση αποτελεσμάτων

Ο παρακάτω πίνακας δείχνει τα αποτελέσματα για το DDM (“Μέθοδος Άμεσης Σχεδίασης”) και τη βελτιστοποίηση οπλισμού από χάλυβα S3D.

Σπιθαμή (ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Λωρίδα στήλης (Σχεδίαση S3D) \({Οπως και ({χιλ}^ 2)}\)	Λωρίδα στήλης (ACI-318 DDM) \({Οπως και ({χιλ}^ 2)}\)	% Διαφ	Μέση Λωρίδα (Σχεδίαση S3D) \({Οπως και ({χιλ}^ 2)}\)	Μέση Λωρίδα (ACI-318 DDM) \({Οπως και ({χιλ}^ 2)}\)	% Διαφ
Εξωτερικό Αρνητικό ES	1012.27	853.996	15.636	238.18	0 (612.0)	100.00
Θετικό ΕΣ	927.80	1018.259	9.75	876.26	689.733	21.287
Εσωτερικό Αρνητικό ES	1786.36	1740.844	2.48	833.63	558.322 (612.0)	26.586
Θετικό ΕΙΝΑΙ	618.54	689.733	11.51	515.44	459.937 (612.0)	18.734
Αρνητικό IS	1667.27	1609.607	3.459	833.63	525.642 (612.0)	26.586

Εγκάρσια κατεύθυνση

Σπιθαμή (ES:Εξωτερικός, ΕΙΝΑΙ:Εσωτερικό)	Λωρίδα στήλης (Σχεδίαση S3D) \({Οπως και ({χιλ}^ 2)}\)	Λωρίδα στήλης (ACI-318 DDM) \({Οπως και ({χιλ}^ 2)}\)	% Διαφ	Μέση Λωρίδα (Σχεδίαση S3D) \({Οπως και ({χιλ}^ 2)}\)	Μέση Λωρίδα (ACI-318 DDM) \({Οπως και ({χιλ}^ 2)}\)	% Διαφ
Εξωτερικό Αρνητικό ES	595.055	518.726	12.827	457.74	0 (1224)	100.00
Θετικό ΕΣ	524.38	618.494	17.948	689.18	418.958	39.209
Εσωτερικό Αρνητικό ES	1327.43	1057.509	20.334	549.29	339.247	38.239
Θετικό ΕΙΝΑΙ	344.60	418.958	21.578	419.50	279.42	33.392
Αρνητικό IS	1327.43	977.799	26.339	549.29	319.189	41.891

συμπέρασμα

Έχουμε αποδείξει σε αυτό το άρθρο ότι η μονάδα SkyCiv για σχεδιασμό πλάκας υπολογίζει τον χαλύβδινο οπλισμό για κάμψη πλάκας σύμφωνα με τον κωδικό ACI-318-19. Σύγκριση των αποτελεσμάτων από την ανάλυση στις λωρίδες στηλών, όπου λόγω της σχετικής ακαμψίας τους, οι στιγμές είναι ιδιαίτερα συγκεντρωμένες, οι διαφορές μεταξύ υπολογισμών με το χέρι και βελτιστοποίησης από S3D γύρω από μια τιμή 10 – 15%. Αυτή η πρακτικότητα υποδηλώνει εξαιρετική αντιστοίχιση μεταξύ των διαδικασιών ανάλυσης και σχεδιασμού.

Για μεσαίες λωρίδες, τα αποτελέσματα διαφέρουν λίγο περισσότερο επειδή ο κωδικός εκχωρεί την υπόλοιπη στιγμή μόνο μετά τη λήψη των αντίστοιχων λωρίδων στηλών. Αυτό θα επηρεάσει την αντιστοίχιση όταν τη συγκρίνουμε με την ανάλυση από το λογισμικό, που είναι πιο ακριβές.

Νέο στο SkyCiv? Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!

Εγγραφείτε στο SkyCiv!