Εκτίμηση χωρητικότητας πασσάλων
Η εκτίμηση της ικανότητας μεταφοράς του σωρού είναι απαραίτητη για τον προσδιορισμό του τελικού αξονικού φορτίου που μπορεί να μεταφέρει ο πάσσαλος. Η απόλυτη ικανότητα φόρτωσης του σωρού (Ερ) ισοδυναμεί με το άθροισμα της φέρουσας ικανότητας στο τέλος (Qp) και αντίσταση τριβής (Qs), που αντιπροσωπεύεται από το Σχ. 1 και Εξ. 1. Πολυάριθμες δημοσιευμένες μελέτες και πρακτικές καθορίζουν την φέρουσα ικανότητα και την αντίσταση τριβής του σωρού. Αυτό το άρθρο εστιάζει σε διάφορες μεθόδους για την εκτίμηση της τελικής χωρητικότητας πασσάλων.
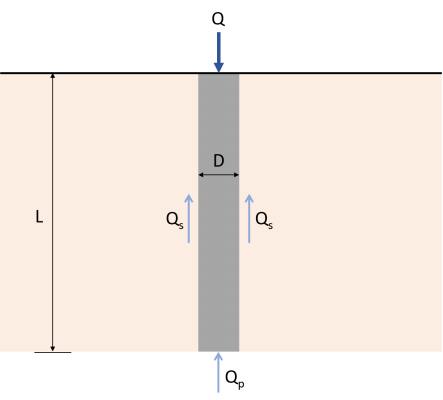
\( {Ερ}_{εσύ} = {Ερ}_{Π} + {Ερ}_{μικρό} \) (1)
Ερεσύ : Απόλυτη ικανότητα μεταφοράς φορτίου
ΕρΠ : Αντοχή φορτίου στο τέλος
Ερμικρό : Αντοχή στην τριβή του δέρματος
Καθολικές εξισώσεις για το QΠ και Qμικρό
\( {Ερ}_{Π} = {ΕΝΑ}_{Π} \φορές {ε}_{Π} \) (2)
\( {ε}_{Π} = (c φορές {Ν}_{ντο}) + (ε’ \φορές {Ν}_{ε}) + (\γάμμα φορές Δ φορές {Ν}_{\γάμμα}) \) (3)
\( {Ερ}_{Π} = {ΕΝΑ}_{Π} \φορές[ (c φορές {Ν}_{ντο}) + (ε’ \φορές {Ν}_{ε}) ] \) (4)
Η συνολική αντίσταση τριβής του σωρού, που αναπτύσσεται κατά μήκος του, μπορεί να υπολογιστεί χρησιμοποιώντας αυτή την εξίσωση:
\( {Ερ}_{μικρό} = ∑ (p × ΔL × f) \) (5)
Π: Περίμετρος του σωρού
μεγάλο: Αυξητικό μήκος πασσάλου πάνω από το οποίο λαμβάνονται τα p και f
φά: Μονάδα αντίστασης τριβής σε οποιοδήποτε βάθος
Μέθοδοι Εκτίμησης Qp
Μέθοδος Meyerhof
Αμμώδη εδάφη
Σύμφωνα με τον Meyerhof, την αντίσταση μοναδιαίου σημείου (εΠ) των πασσάλων στην άμμο γενικά αυξάνεται με το μήκος ενσωμάτωσης έως ότου φτάσει στη μέγιστη τιμή του όταν ο λόγος ενσωμάτωσης (L/D) φτάνει σε κρίσιμη τιμή. Κρίσιμη αναλογία ενσωμάτωσης (L/D)Ενώ το Restraint θα απαιτήσει να εισαγάγετε το συνήθως ποικίλλει από 16 προς το 18. Σε αυτή τη μέθοδο, Οι σωροί στην άμμο υποτίθεται ότι έχουν μηδενική συνοχή (c ≈ 0), και η αντίσταση μοναδιαίου σημείου δεν πρέπει να υπερβαίνει την αντίσταση οριακού σημείου (εμεγάλο), που δίνεται από την Εξ. 7. Ο συντελεστής φέρουσας ικανότητας (Αρ) Οι τιμές είναι ευθέως ανάλογες με τη γωνία τριβής του εδάφους του φέροντος στρώματος (Τραπέζι 1). Βασισμένο στη θεωρία του Meyerhof, η καθολική εξίσωση για το QΠ (Εξ.4) μπορεί να απλοποιηθεί σε:
\( {Ερ}_{Π} = {ΕΝΑ}_{Π} \φορές (ε’ \φορές {Ν}_{ε}) \leq ({ΕΝΑ}_{Π} \φορές {ε}_{μεγάλο}) \) (6)
\( {ε}_{μεγάλο} = 0.5 \φορές {Π}_{ένα} \φορές {Ν}_{ε} \φορές μαύρισμα (\φι') \) (7)
εμεγάλο : Αντίσταση οριακού σημείου
Πένα: Ατμοσφαιρική πίεση (≈100 kN/m2)
\( \phi’\): Αποτελεσματική γωνία τριβής εδάφους στην άκρη του σωρού
Τραπέζι 1: Οι παρεμβαλλόμενες τιμές του Nε (Η θεωρία του Meyerhof)
Αργιλώδες χώμα
Εξίσωση 4 μπορεί επίσης να υπολογίσει την τελική φέρουσα ικανότητα πασσάλων σε αργιλώδη ή συνεκτικά εδάφη (φ ≈ 0). Δεδομένου ότι η γωνία τριβής του εδάφους αγνοείται και ο συντελεστής φέρουσας ικανότητας (Νντο) έχει σταθερή τιμή 9 για συνεκτικά εδάφη, Η εξ.4 μπορεί να γραφεί ως:
\( {Ερ}_{Π} = {ΕΝΑ}_{Π} \φορές c φορές {Ν}_{ντο} = 9 \φορές c φορές {ΕΝΑ}_{Π} \) (8)
Μέθοδος Vesic
Η μέθοδος του Vesic για τον υπολογισμό της τελικής φέρουσας ικανότητας σε αμμώδη ή αργιλώδη εδάφη βασίζεται στη θεωρία του για τη διαστολή των κοιλοτήτων.
Αμμώδη εδάφη
Με βάση τη θεωρία του, Η τελική φέρουσα ικανότητα των πασσάλων στην άμμο μπορεί να εκτιμηθεί χρησιμοποιώντας τις ακόλουθες εξισώσεις:
\( {Ερ}_{Π} = {ΕΝΑ}_{Π} \φορές bar{\σίγμα»}_{ο} \φορές {Ν}_{\σίγμα} \) (9)
\(\μπαρ{\σίγμα»}_{ο} = frac{1 + (2 \φορές {κ}_{ο})}{3} \φορές q') (10)
\( {κ}_{ο} = 1 – sin \phi’\) (11)
\( {Ν}_{\σίγμα} = frac{3 \φορές {Ν}_{ε}}{1 + (2 \φορές {κ}_{ο})} \) (12)
\(\μπαρ{\σίγμα»}_{ο} \) : Μέση αποτελεσματική κανονική τάση εδάφους στο επίπεδο του σημείου πασσάλου
Είναι: Συντελεστής πίεσης γης σε ηρεμία
Nσ: Συντελεστής φέρουσας ικανότητας
Αργιλώδες χώμα
Το ίδιο και η μέθοδος του Meyerhof, Εξ. 4 ισχύει επίσης για τον υπολογισμό της τελικής φέρουσας ικανότητας πασσάλων σε πηλό. Ωστόσο, την τιμή του συντελεστή φέρουσας ικανότητας (Νντο) είναι ένας παράγοντας δείκτη ακαμψίας (Εγώρ). Σύμφωνα με τη θεωρία του για διαστολή των κοιλοτήτων, Νντο και εγώρ μπορεί να εκτιμηθεί από:
\( {Ν}_{ντο} = (\frac{4}{3}) \φορές [στο({Εγώ}_{ρ}) + 1] + \frac{\πι}{2} + 1 \) (13)
\( {Εγώ}_{ρ} = frac{{μι}_{μικρό}}{3 \φορές γ} \) (Για φ ≈ 0)(14)
Εγώρ: Δείκτης ακαμψίας
μιμικρό: Μέτρο ελαστικότητας εδάφους
Μέθοδος Coyle και Castello (Αμμώδη εδάφη)
Βασισμένο στο 24 μεγάλης κλίμακας δοκιμές φορτίου πεδίου οδηγημένων πασσάλων στην άμμο, Οι Coyle και Castello πρότειναν ότι η φέρουσα ικανότητα των πασσάλων μπορεί να υπολογιστεί χρησιμοποιώντας την Εξ. 15. Οι τιμές του συντελεστή φέρουσας ικανότητας (Αρ) είναι ένας παράγοντας και των δύο αναλογιών ενσωμάτωσης (L/D) και τη γωνία τριβής του εδάφους (φ’), όπως φαίνεται στο Σχ. 2
\( {Ερ}_{Π} = {ΕΝΑ}_{Π} \φορές (ε’ \φορές {Ν}_{ε}) \) (15)
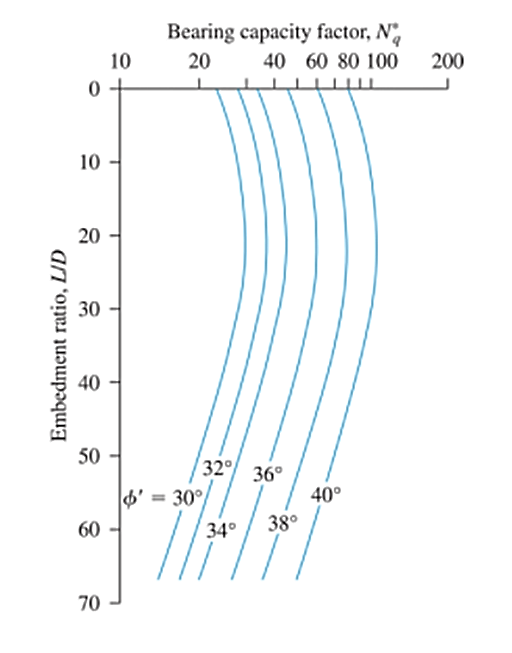
Φιγούρα 2: Παραλλαγή του Nq με L/D & φ’ (Επανασχεδιασμένο μετά τον Coyle & Καστέλο, 1981)
Πηγή: ο, Μπράγια. Αρχές Μηχανικής του Ιδρύματος (7ου Έκδοση, σελ.564)
Μέθοδοι Εκτίμησης Qs
Αντίσταση τριβής πασσάλων στην άμμο
Η μονάδα αντίστασης τριβής των πασσάλων στην άμμο, όπως φαίνεται στην Εξ. 5, λαμβάνει υπόψη πολλούς παράγοντες που είναι αρκετά δύσκολο να υπολογιστούν. Περιλαμβάνει τον συντελεστή πίεσης γείωσης (κ) & γωνία τριβής εδάφους-σωρού, οι οποίες και οι δύο έχουν ποικίλες τιμές ανάλογα με την προσέγγιση που θα χρησιμοποιηθεί ή με τα διαθέσιμα δεδομένα εδάφους.
\( f = K φορές {\σίγμα}_{ο}’ \φορές μαύρισμα (\δέλτα) \) (15)
κ: Πραγματικός συντελεστής πίεσης γείωσης
σ’ο: Αποτελεσματική κατακόρυφη τάση στο υπό εξέταση βάθος
δ: Γωνία τριβής εδάφους-σωρού
Ακολουθούν οι διάφοροι τρόποι εκτίμησης του πραγματικού συντελεστή πίεσης γης και των τιμών της γωνίας εδάφους-τριβής. Αυτές οι μεταβλητές αποτελούν παράγοντα γωνίας τριβής του εδάφους (φ’) ή τύπου πασσάλου.
Πραγματικός συντελεστής πίεσης γείωσης
Το έδαφος ασκεί πλευρική πίεση γείωσης στην επιφάνεια του σωρού. Είναι απαραίτητο να ληφθεί υπόψη αυτή η πίεση στο σχεδιασμό ή την ανάλυση για σταθερότητα. Οι παρακάτω είναι οι διαφορετικοί τρόποι για τον προσδιορισμό των συντελεστών πίεσης γης για τον υπολογισμό της αντίστασης τριβής μονάδας πασσάλων στην άμμο.
NAVFAC DM 7.2
| Τύπος σωρού | Συμπίεση | Ανύψωση |
|---|---|---|
Τραπέζι 2: Συντελεστής πίεσης γης, κ (NAVFAC DM 7.2)
Μέθοδος Μέσης Κ
Ο συντελεστής πίεσης γείωσης (κ) μπορεί επίσης να εκτιμηθεί λαμβάνοντας τον μέσο όρο του συντελεστή πίεσης γείωσης σε κατάσταση ηρεμίας (κ0), ενεργή πίεση γείωσης (κένα), και παθητική πίεση γείωσης (κΠ), όπως φαίνεται από τις Εξισώσεις 16-19.
\( K =frac{{κ}_{0} + {κ}_{ένα} + {κ}_{Π}}{3} \) (16)
\( (κ)_{0} =1 – αμαρτία φι \) (17)
\( (Κ_{ένα} =1 – {βυρσοδέψω}^{2}( \frac{45 – \phi}{2}) \) (18)
\( (Κ_{Π} =1 + {βυρσοδέψω}^{2}( \frac{45 + \phi}{2}) \) (19)
Μανσούρ και Χάντερ (1970)
Με βάση τα διαφορετικά αποτελέσματα δοκιμής φορτίου πεδίου, Οι Mansur και Hunter ολοκλήρωσαν τις τιμές του συντελεστή πίεσης γείωσης με τους αντίστοιχους τύπους πασσάλων.
| Τύπος σωρού | κ |
|---|---|
Τραπέζι 3: Συντελεστής πίεσης γης, κ (Μανσούρ και Χάντερ, 1970)
Γωνία τριβής εδάφους-σωρού
Η γωνία τριβής μεταξύ του εδάφους και της επιφάνειας του σωρού είναι μια ουσιαστική πτυχή του σχεδιασμού της θεμελίωσης. Πρακτικά, Πολλοί μηχανικοί προσεγγίζουν αυτή την τιμή ως ίση με 2/3 της εσωτερικής γωνίας τριβής του εδάφους. Ωστόσο, με βάση τη μελέτη των Coyle και Castello στο 1981, η γωνία τριβής εδάφους-σωρού είναι περίπου ισοδύναμη με 80% της εσωτερικής γωνίας τριβής του εδάφους. Αφ 'ετέρου, Το NAVFAC DM7.2 χρησιμοποιεί αυτές τις τιμές για να εκτιμήσει τη γωνία τριβής μεταξύ του εδάφους και του σωρού:
| Τύπος σωρού | δ |
|---|---|
Τραπέζι 4: Γωνία τριβής εδάφους-σωρού (δ) (NAVFAC DM 7.2)
Αντίσταση τριβής πασσάλων σε άργιλο
Ο υπολογισμός της αντίστασης τριβής των πασσάλων σε αργιλώδη εδάφη μπορεί να είναι τόσο δύσκολος όσο αυτός στα αμμώδη εδάφη λόγω της εισαγωγής νέων μεταβλητών, που επίσης δεν είναι τόσο εύκολο να προσδιοριστούν. Ωστόσο, Υπάρχουν πολλές διαθέσιμες μέθοδοι για να λάβετε τις τιμές αυτών των μεταβλητών.
λ Μέθοδος
Με βάση τη μελέτη των Vijayvergiya και Focht στο 1972, η συνολική αντίσταση τριβής των πασσάλων στον πηλό μπορεί να υπολογιστεί με τον προσδιορισμό της μέσης μονάδας αντίστασης τριβής του σωρού, όπως φαίνεται από τις Εξισώσεις 20 και 21. Οι τιμές λ αλλάζουν καθώς αυξάνεται το βάθος διείσδυσης του σωρού. Τραπέζι 5 δείχνει τη διακύμανση του λ με το μήκος ενσωμάτωσης του σωρού.
\( {φά}_{του} = λάμδα φορές [\μπαρ{\σίγμα»}_{ο} +( 2 \φορές {ντο}_{εσύ})] \) (20)
\({Ερ}_{μικρό} = p times L times {φά}_{του} \) (21)
\( \μπαρ{\σίγμα»}_{ο} \): Μέση αποτελεσματική κατακόρυφη τάση για ολόκληρο το μήκος ενσωμάτωσης
ντοεσύ: Μέση μη στραγγιζόμενη διατμητική αντοχή
| μεγάλο (Μ) | λ |
|---|---|
Τραπέζι 5: Παραλλαγή του λ με μήκος ενσωμάτωσης πασσάλων (μεγάλο)
α Μέθοδος
Η μέθοδος α προτείνει ότι η μονάδα αντίστασης τριβής των πασσάλων είναι ισοδύναμη με το γινόμενο της μη στραγγιζόμενης συνοχής του εδαφικού στρώματος και του αντίστοιχου εμπειρικού συντελεστή πρόσφυσης (α). Τραπέζι 6 δείχνει την αντίστοιχη τιμή του συντελεστή πρόσφυσης με την αναλογία μη στραγγιζόμενης συνοχής και ατμοσφαιρικής πίεσης (ντοεσύ/Πένα).
\(f = \alpha \times {ντο}_{εσύ}\) (22)
Επομένως, η συνολική αντίσταση τριβής του σωρού σε πηλό χρησιμοποιώντας αυτή τη μέθοδο μπορεί να ξαναγραφεί ως:
\({Ερ}_{μικρό} = άθροισμα (f \times p \times \Delta L) = άθροισμα (\alpha \times {ντο}_{εσύ} \times p \times \Delta L)\) (23)
| ντοεσύ/Πένα | α |
|---|---|
| 0.8 | |
Πένα = ατμοσφαιρική πίεση ≈ 100 kN / m2
Τραπέζι 6: Παραλλαγή του α (Terzaghi, Τσιμπώ, και Mesri, 1996)
β Μέθοδος
Η πίεση του νερού στους πόρους γύρω από το σωρό αυξάνεται όταν ο σωρός οδηγείται σε κορεσμένους αργίλους. Αυτή η μέθοδος, βασίζεται σε αποτελεσματική ανάλυση στρες, είναι κατάλληλο για μακροχρόνια (στραγγισμένο) αναλύει τη χωρητικότητα φορτίου πασσάλων καθώς λαμβάνει υπόψη τη σταδιακή διάχυση της υπερβολικής πίεσης νερού πόρων με την πάροδο του χρόνου. Σύμφωνα με τον Tomlinson (1971), οι σωροί που οδηγούνται σε μαλακούς άργιλους υποθέτουν ότι συμβαίνουν αστοχίες στο αναμορφωμένο έδαφος κοντά στην επιφάνεια του πασσάλου. Με βάση την Εξ. 15, ο όρος (Κ × τανδ) για τη μονάδα αντίστασης τριβής των πασσάλων στην άμμο θα αντιπροσωπεύεται από το β. Η γωνία εδάφους-τριβής (δ) θα αντικατασταθεί από μια αναδιαμορφωμένη στραγγισμένη γωνία τριβής του εδάφους (Φ’Ρ). Έτσι η μονάδα αντίστασης τριβής των πασσάλων στον πηλό εκτιμάται ότι είναι ίση με:
\(f = beta φορές {\σίγμα»}_{ο}\) (24)
\(\βήτα = Κ φορές μαύρισμα {\Phi'}_{Ρ}\) (25)
Συντηρητικά, ο συντελεστής πίεσης γείωσης (κ) ισοδυναμεί με τον συντελεστή πίεσης γείωσης σε κατάσταση ηρεμίας (κ0) η οποία ποικίλλει για κανονικά στερεοποιημένους αργίλους και υπερσυμπαγείς αργίλους, όπως φαίνεται στις παρακάτω εξισώσεις:
\( Κ = {κ}_{0} = 1 – χωρίς {\Phi'}_{Ρ}\) (Κανονικά ενοποιημένοι άργιλοι) (26)
\( Κ = {κ}_{0} = (1 – χωρίς {\Phi'}_{Ρ}) \φορές sqrt(OCR)\) (Υπερσυμπυκνωμένοι άργιλοι) (27)
OCR: Αναλογία υπερενοποίησης
Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς μεταφοράς φορτίου χωρίς καμία λήψη ή εγκατάσταση!
βιβλιογραφικές αναφορές:
- ο, Π.Μ.. (2007). Αρχές Μηχανικής του Ιδρύματος (7ου Έκδοση). Παγκόσμια Μηχανική
- Rajapakse, Ρ. (2016). Σχεδιασμός και κατασκευή κανόνα σωρού του αντίχειρα (2nd Έκδοση). Elsevier Inc..
- Τομλίνσον, Μ.Γ.. (2004). Πρακτική σχεδιασμού και κατασκευής σωρών (4ου Έκδοση). μι & FN Spon.


