Πώς να υπολογίσετε την τελική ικανότητα φόρτωσης ενός μόνο σωρού

Ικανότητα μεταφοράς φορτίου

---

Η αξιολόγηση της απόλυτης ικανότητας μεταφοράς φορτίου ενός μόνο σωρού είναι μια από τις πιο σημαντικές πτυχές του σχεδιασμού των σωρών, και μερικές φορές μπορεί να είναι περίπλοκη. Αυτό το άρθρο θα εξετάσει τις εξισώσεις που ισχύουν για το σχεδιασμό μονής στοίβας, καθώς και ένα παράδειγμα.

Για να κατανοήσετε εύκολα τον μηχανισμό μεταφοράς φορτίου ενός μόνο σωρού, φανταστείτε ένα σωρό από σκυρόδεμα μήκους L με διάμετρο D, όπως φαίνεται στο σχήμα 1.

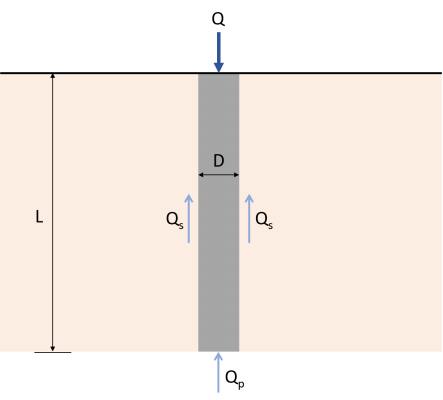
Φιγούρα 1: Μηχανισμός μεταφοράς φορτίου για πασσάλους

Το φορτίο Q που εφαρμόζεται στο σωρό μεταφέρεται απευθείας στο έδαφος στο κάτω μέρος του σωρού. Μέρος αυτού του φορτίου θα αντισταθεί από τις πλευρές του σωρού χρησιμοποιώντας κάτι που ονομάζεται “τριβή του δέρματος” αναπτύχθηκε κατά μήκος του άξονα (Ερ_μικρό), και τα υπόλοιπα θα αντισταθούν από το έδαφος στο οποίο φέρει ο σωρός (Ερ_Π). Επομένως, την απόλυτη ικανότητα μεταφοράς φορτίου (Ερ) ενός σωρού δίνεται από την εξίσωση (1). Υπάρχουν πολλές διαθέσιμες μέθοδοι για την εκτίμηση των τιμών του Q_Π και Q_μικρό.

\( {Ερ}_{εσύ} = {Ερ}_{Π} + {Ερ}_{μικρό} \) (1)

Ερ_εσύ = Απόλυτη ικανότητα μεταφοράς φορτίου

Ερ_Π = Ικανότητα φορτίου στο τέλος

Ερ_μικρό = Αντοχή στην τριβή του δέρματος

Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς μεταφοράς φορτίου χωρίς καμία λήψη ή εγκατάσταση!

Υπολογιστής σχεδίασης ιδρύματος

Ικανότητα άκρου, Ερ_Π

---

Η απόλυτη τελική ικανότητα είναι θεωρητικά το μέγιστο φορτίο ανά μονάδα επιφάνειας που μπορεί να υποστηριχθεί από το έδαφος στο ρουλεμάν, χωρίς αποτυχία. Η ακόλουθη εξίσωση του Karl Von Terzaghi, ο πατέρας της μηχανικής του εδάφους, είναι μια από τις πρώτες και πιο συχνά χρησιμοποιούμενες θεωρίες κατά την αξιολόγηση της τελικής φέρουσας ικανότητας των θεμελίων. Η εξίσωση του Terzaghi για την τελική φέρουσα ικανότητα μπορεί να εκφραστεί ως:

\( {ε}_{εσύ} = (γ × {Ν}_{ντο}) + (q × {Ν}_{ε}) + (\frac{1}{2} × γ × B × {Ν}_{γ}) \) (2)

ε_εσύ = Απόλυτη τελική ικανότητα

c = Συνοχή του εδάφους

q = Αποτελεσματική πίεση εδάφους

γ = μοναδιαίο βάρος εδάφους

B = Βάθος ή διάμετρος διατομής

Ν_ντο, Ν_ε, Ν_γ = Συντελεστές ρουλεμάν

Από το q_εσύ είναι σε όρους φορτίου ανά μονάδα επιφάνειας ή πίεσης, Ο πολλαπλασιασμός του με την περιοχή διατομής του σωρού θα έχει ως αποτέλεσμα την ικανότητα φόρτωσης του άκρου (Ερ_Π) του σωρού. Η προκύπτουσα τιμή του τελευταίου όρου της Εξίσωσης 2 είναι αμελητέο λόγω ενός σχετικά μικρού πλάτους σωρού, ως εκ τούτου, μπορεί να απορριφθεί από την εξίσωση. Ετσι, Η τελική φέρουσα ικανότητα φορτίου του σωρού μπορεί να εκφραστεί όπως φαίνεται στην εξίσωση (3). Αυτή η τροποποιημένη έκδοση της εξίσωσης του Terzaghi χρησιμοποιείται στην ενότητα SkyCiv Foundation κατά το σχεδιασμό πασσάλων.

\( {Ερ}_{Π} = {ΕΝΑ}_{Π} × [(γ × {Ν}_{ντο}) + (q × {Ν}_{ε}) ] \) (3)

ΕΝΑ_Π = Εμβαδόν διατομής του σωρού

Συντελεστές ρουλεμάν N_ντο και Ν_ε είναι μη διαστατικά, εμπειρικά, και είναι λειτουργίες της γωνίας τριβής του εδάφους (Φ). Οι ερευνητές έχουν ήδη ολοκληρώσει τους υπολογισμούς που απαιτούνται για να βρουν φέροντες παράγοντες. Τραπέζι 1 συνοψίζει τις τιμές του Ν_ε σύμφωνα με τη Διοίκηση Μηχανικών Ναυτικών Εγκαταστάσεων (NAVFAC DM 7.2, 1984). Η τιμή του Ν_ντο είναι περίπου ίσο με 9 για σωρούς κάτω από αργιλώδη εδάφη.

Συντελεστής ρουλεμάν (Νε)
Γωνία τριβής (Ø)	26	28	30	31	32	33	34	35	36	37	38	39	40
Οδηγημένοι σωροί	10	15	21	24	29	35	42	50	62	77	86	120	145
Βαρεμένοι σωροί	5	8	10	12	14	17	21	25	30	38	43	60	72

Τραπέζι 1: Ν_ε τιμές από NAVFAC DM 7.2

Ικανότητα αντίστασης σε τριβή του δέρματος, Ερ_μικρό

---

Η αντίσταση του δέρματος στην τριβή των πασσάλων αναπτύσσεται κατά μήκος του σωρού. Γενικά, η αντίσταση τριβής ενός σωρού εκφράζεται ως:

\( {Ερ}_{μικρό} = ∑ (p × ΔL × f) \) (4)

p = Περίμετρος του σωρού

ΔL = Αυξημένο μήκος πασσάλου πάνω από το οποίο λαμβάνονται τα p και f

f = Αντίσταση τριβής μονάδας σε οποιοδήποτε βάθος

Εκτίμηση της τιμής της αντίστασης τριβής της μονάδας (φά) απαιτεί πολλούς σημαντικούς παράγοντες που πρέπει να ληφθούν υπόψη, όπως η φύση της εγκατάστασης των σωρών και η ταξινόμηση του εδάφους. Εξισώσεις (5) και (6) δείχνει την υπολογιστική μέθοδο για να βρείτε τη μονάδα αντίστασης τριβής σε σωρούς σε αμμώδη και αργιλώδη εδάφη, αντίστοιχα. Πίνακες 2 και 3 παρουσιάστε τον συνιστώμενο αποτελεσματικό συντελεστή πίεσης γείωσης (κ) και η γωνία τριβής του εδάφους-σωρού (δ’), σύμφωνα με το NAVFAC DM7.2.

Για αμμώδη εδάφη:

\( f = Κ × σ ’× μαύρισμα(δ’) \) (5)

K = Αποτελεσματικός συντελεστής πίεσης γείωσης

σ’ = Αποτελεσματική κατακόρυφη τάση στο υπό εξέταση βάθος

δ’ = Γωνία τριβής του εδάφους-σωρού

Για αργιλώδη εδάφη:

\( f = α × γ \) (6)

α = Εμπειρικός συντελεστής πρόσφυσης

Γωνία τριβής εδάφους-σωρού (δ’)
Τύπος σωρού	δ’
Σωρός από χάλυβα	20º
Ξυλεία στοίβα	3/4 × Φ
Σωρός σκυροδέματος	3/4 × Φ

Τραπέζι 2: Τιμές τριβής εδάφους-σωρού (NAVFAC DM7.2, 1984)

Συντελεστής πλευρικής πίεσης γης (κ)
Τύπος σωρού	Σωρός συμπίεσης	Σωρός έντασης
Οδήγησε H-σωρούς	0.5-1.0	0.3-0.5
Οδηγημένοι σωροί μετατόπισης (γύρος, ορθογώνιος)	1.0-1.5	0.6-1.0
Οδηγημένοι σωροί μετατόπισης (κωνικό)	1.5-2.0	1.0-1.3
Οδηγημένοι σωροί	0.4-0.9	0.3-0.6
Βαρεμένοι σωροί (<24″ Διάμετρος)	0.7	0.4

Τραπέζι 3: Συντελεστής πλευρικής πίεσης γης (κ) Αξίες (NAVFAC DM7.2, 1984)

Συντελεστής πρόσφυσης (α)
γ / σένα	α
≤ 0.1	1.00
0.2	0.92
0.3	0.82
0.4	0.74
0.6	0.62
0.8	0.54
1.0	0.48
1.2	0.42
1.4	0.40
1.6	0.38
1.8	0.36
2.0	0.35
2.4	0.34
2.8	0.34

Σημείωση: Π_ένα = ατμοσφαιρική πίεση ≈ 100 kN / m²

Τραπέζι 4: Τιμές συντελεστών πρόσφυσης (Terzaghi, Τσιμπώ, και Mesri, 1996)

Παράδειγμα: Υπολογίζοντας την ικανότητα των πασσάλων στην άμμο

---

Ένας σωρός σκυροδέματος μήκους 12 μέτρων με διάμετρο 500 Το mm οδηγείται σε πολλαπλά στρώματα άμμου χωρίς να υπάρχουν υπόγεια νερά. Βρείτε την απόλυτη ικανότητα μεταφοράς φορτίου (Ερ_εσύ) του σωρού.

Λεπτομέριες
Ενότητα
Διάμετρος	500 χιλ
Μήκος	12 Μ
Ιδιότητες στρώματος 1-εδάφους
Πάχος	5 Μ
Βάρος μονάδας	17.3 kN / m3
Γωνία τριβής	30 Βαθμοί
Συνοχή	0 kPa
Πίνακας υπόγειων υδάτων	Απών
Ιδιότητες στρώματος 2-εδάφους
Πάχος	7 Μ
Βάρος μονάδας	16.9 kN / m3
Γωνία τριβής	32 Βαθμοί
Συνοχή	0 kPa
Πίνακας υπόγειων υδάτων	Απών

Βήμα 1: Υπολογίστε την ικανότητα φορτίου του άκρου (Ερ_Π).

Στην άκρη του σωρού:

ΕΝΑ_Π = (π/4) × Δ² = (π/4) × 0.5²

ΕΝΑ_Π = 0.196 Μ²

γ = 0 kPa

θ = 32º

Ν_ε = 29 (Από τον πίνακα 1)

Αποτελεσματική πίεση εδάφους (ε):

q = (γ₁ × τ₁) + (γ₂ × τ₂) = (5 m × 17.3 kN / m³) + (7 m × 16.9 kN / m³)

q = 204.8 kPa

Στη συνέχεια χρησιμοποιήστε εξίσωση (3) για το φορτίο τελικής ικανότητας:

Ερ_Π = ΕΝΑ_Π × [(c × Ν_ντο) + (q × Ν_ε)]

Ερ_Π = 0.196 Μ² × ( 204.8 KPa × 29)

Ερ_Π = 1,164.083 ΚΝ

Βήμα 2: Υπολογίστε την αντοχή στην τριβή του δέρματος (Ερ_μικρό).

Χρησιμοποιώντας εξισώσεις (4) και (5), υπολογίστε την τριβή του δέρματος ανά στρώση εδάφους.

Ερ_μικρό = ∑ (p × ΔL × f)

p = π × D = π × 0.5 Μ

ρ = 1.571 Μ

Στρώμα 1:

ΔL = 5 Μ

φά₁ = K × σ’₁× μαύρισμα(δ’)

Κ = 1.25 (Τραπέζι 3)

δ’ = 3/4 × 30º

δ’ = 22,50º

σ’₁ = γ₁ × (0.5 × τ₁) = 17.3 kN / m³ × (0.5 × 5 Μ)

σ’₁ = 43.25 kN / m²

φά₁ = 1.25 × 43.25 kN / m² × μαύρισμα(22.50º)

φά₁ = 22.393 kN / m²

Ερ_s1 = p × ΔL × f₁ = 1.571 m × 5 m × 22.393 kN / m²

Ερ_s1 = 175.897 ΚΝ

Στρώμα 2:

ΔL = 7 Μ

φά₂ = K × σ’₂× μαύρισμα(δ’)

Κ = 1.25 (Τραπέζι 3)

δ’ = 3/4 × 32º

δ’ = 24º

σ’₂ = (γ₁ × τ₁) + [γ₂ × (0.5 × τ₂)] = (17.3 kN / m³ × 5 Μ) + [16.9 kN / m³ ×(0.5 × 7 Μ)]

σ’₂ = 145.65 kN / m²

φά₂ = 1.25 × 145.65 kN / m² × μαύρισμα(24º)

φά₂ = 81.059 kN / m²

Ερ_δ2 = p × ΔL × f₂ = 1.571 m × 7 m × 81.059 kN / m²

Ερ_δ2 = 891.406 ΚΝ

Ολική αντοχή σε τριβές του δέρματος:

Ερ_μικρό = Ε_s1+ Ερ_δ2 = 175.897 ΚΝ + 891.406 ΚΝ

Ερ_μικρό = 1,067.303 ΚΝ

Βήμα 3: Υπολογίστε για την απόλυτη ικανότητα μεταφοράς φορτίου (Ερ_εσύ).

Ερ_εσύ = Ε_Π+ Ερ_μικρό = 1,164.083 ΚΝ + 1,067.303 ΚΝ

Ερ_εσύ = 2,231.386 ΚΝ

Παράδειγμα 2: Υπολογίζοντας την ικανότητα των πασσάλων σε πηλό

---

Εξετάστε ένα 406 Σωρός σκυροδέματος διαμέτρου mm με μήκος 30m ενσωματωμένο σε στρώσεις, κορεσμένος πηλός. Βρείτε την απόλυτη ικανότητα μεταφοράς φορτίου (Ερ_εσύ) του σωρού.

Λεπτομέριες
Ενότητα
Διάμετρος	406 χιλ
Μήκος	30 Μ
Ιδιότητες στρώματος 1-εδάφους
Πάχος	10 Μ
Βάρος μονάδας	8 kN / m3
Γωνία τριβής	0º
Συνοχή	30 kPa
Πίνακας υπόγειων υδάτων	5 Μ
Ιδιότητες στρώματος 2-εδάφους
Πάχος	10 Μ
Βάρος μονάδας	19.6 kN / m3
Γωνία τριβής	0º
Συνοχή	0 kPa
Πίνακας υπόγειων υδάτων	Πλήρως βυθισμένο

Βήμα 1: Υπολογίστε την ικανότητα φορτίου του άκρου (Ερ_Π).

Στην άκρη του σωρού:

ΕΝΑ_Π = (π/4) × Δ²= (π/4) × 0.406²

ΕΝΑ_Π = 0.129 Μ²

γ = 100 kPa

Ν_ντο = 9 (Τυπική τιμή για πηλό)

Ερ_Π = (c × Ν_ντο) × Α_Π = (100 kPa × 9) × 0.129 Μ²

Ερ_Π = 116.1 ΚΝ

Βήμα 2: Υπολογίστε την αντοχή στην τριβή του δέρματος (Ερ_μικρό).

Χρησιμοποιώντας εξισώσεις (4) και (6), υπολογίστε την τριβή του δέρματος ανά στρώση εδάφους.

Ερ_μικρό = ∑ (p × ΔL × f)

p = π × D = π × 0.406 Μ

ρ = 1.275 Μ

Στρώμα 1:

ΔL = 10 Μ

α₁ = 0.82 (Τραπέζι 4)

ντο₁ = 30 kPa

φά₁= α₁ × γ₁ = 0.82 × 30 kPa

φά₁ = 24.6 kN / m²

Ερ_s1 = p × ΔL × f₁ = 1.275 m × 10 m × 24.6 kN / m²

Ερ_s1 = 313.65 kN / m²

Στρώμα 2:

ΔL = 20 Μ

α₂= 0.48 (Τραπέζι 4)

ντο₂ = 100 kPa

φά₂ = α₂ × γ₂ = 0.48 × 100 kPa

φά₂ = 48 kN / m²

Ερ_δ2 = p × ΔL × f₂ = 1.275 m × 20 m × 48 kN / m²

Ερ_δ2 = 1,224 kN / m²

Ολική αντοχή σε τριβές του δέρματος:

Ερ_μικρό = Ε_s1+ Ερ_δ2 = 313.65 ΚΝ + 1224 ΚΝ

Ερ_μικρό = 1,537.65 ΚΝ

Βήμα 3: Υπολογίστε για την απόλυτη ικανότητα μεταφοράς φορτίου (Ερ_εσύ).

Ερ_εσύ = Ε_Π+ Ερ_μικρό = 116.1 ΚΝ + 1537.65 ΚΝ

Ερ_εσύ = 1,653.75 ΚΝ

Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς μεταφοράς φορτίου χωρίς καμία λήψη ή εγκατάσταση!

Υπολογιστής σχεδίασης ιδρύματος

βιβλιογραφικές αναφορές:

• ο, Π.Μ.. (2007). Αρχές Μηχανικής του Ιδρύματος (7ου Έκδοση). Παγκόσμια Μηχανική
• Rajapakse, Ρ. (2016). Σχεδιασμός και κατασκευή κανόνα σωρού του αντίχειρα (2nd Έκδοση). Elsevier Inc..
• Τομλίνσον, Μ.Γ.. (2004). Πρακτική σχεδιασμού και κατασκευής σωρών (4ου Έκδοση). μι & FN Spon.