ΕΝΑ Συνδυασμένη βάση είναι ένα μόνο στήριγμα που υποστηρίζει δύο ή περισσότερες στήλες. Οι συνδυασμένες βάσεις χρησιμοποιούνται συνήθως όταν οι στήλες απέχουν πολύ κοντά, όπου δύο απομονωμένες θέσεις δεν θα ήταν ικανοποιητικές. Για παράδειγμα, με δύο απομονωμένες βάσεις που είναι πολύ κοντά το ένα στο άλλο, το έδαφος κάτω μπορεί να μοιράζεται τμήματα των ζωνών επιρροής, οδηγώντας σε μια απαιτούμενη επέκταση ενός ή και των δύο μεμονωμένων βάσεων. Ανάλογα με τους φυσικούς ή άλλους περιορισμούς, αυτό μπορεί να μην είναι δυνατό.

Η ενότητα SkyCiv Foundation Design περιλαμβάνει τη σχεδίαση συνδυασμένων βάσεων σύμφωνα με το American Concrete Institute (ACI 318).

Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς μεταφοράς φορτίου χωρίς καμία λήψη ή εγκατάσταση!

Υπολογιστής σχεδίασης ιδρύματος

Σχεδιασμός Συνδυασμένου Ιδρύματος

Απαιτήσεις διάστασης

Για να προσδιορίσετε τις διαστάσεις μιας απομονωμένης βάσης, σέρβις ή ατέλειωτα φορτία, όπως νεκρός (ρε), Ζω (μεγάλο), Ανεμος (Δ), Σεισμικός (μι), κ.λπ. θα εφαρμοστούν χρησιμοποιώντας συνδυασμούς φορτίων, όπως ορίζεται από την ACI 318-14. Ό, τι κι αν συνδυάζει φορτίο θα θεωρείται το φορτίο σχεδιασμού, και συγκρίνεται με την επιτρεπόμενη πίεση εδάφους όπως φαίνεται στην Εξίσωση 1, όπως συνιστάται στο Ενότητα 13.2.6 της ACI 318-14.

\(\κείμενο{ε}_{\κείμενο{ένα}} = frac{ \κείμενο{Ρ1}_{\κείμενο{ν}} + \κείμενο{Ρ2}_{\κείμενο{ν}} }{\κείμενο{ΕΝΑ}} \δεξί βέλος \) Εξίσωση 1

όπου:
ε_ένα = καθαρή επιτρεπόμενη πίεση εδάφους
Ρ1_ν = αφόρητα φορτία στη στήλη 1 (αριστερά)
Ρ2_ν = αφόρητα φορτία στη στήλη 2 (σωστά)
A = Περιοχή ιδρύματος

Από την εξίσωση 1, ε_ένα ανταλλάσσονται με ΕΝΑ.

\(\κείμενο{ΕΝΑ} = frac{ \κείμενο{Ρ1}_{\κείμενο{ν}} + \κείμενο{Ρ2}_{\κείμενο{ν}} }{\κείμενο{ε}_{\κείμενο{ένα}}} \δεξί βέλος \) Εξίσωση 1α

Σε αυτό το σημείο, Οι διαστάσεις του υποστρώματος μπορούν να υπολογιστούν εκ νέου από την απαιτούμενη διάσταση περιοχής, ΕΝΑ.

Μονόδρομη κουρά

ο Διάτμηση μονής κατεύθυνσης οριακή κατάσταση, γνωστός και ως “κάμψη”, επεκτείνει το κρίσιμο τμήμα σε όλο το πλάτος της βάσης και βρίσκεται σε απόσταση “ρε” από το πρόσωπο μιας στήλης, όπου βρίσκεται το Critical Plane Shear (Ανατρέξτε στην Εικόνα 1).

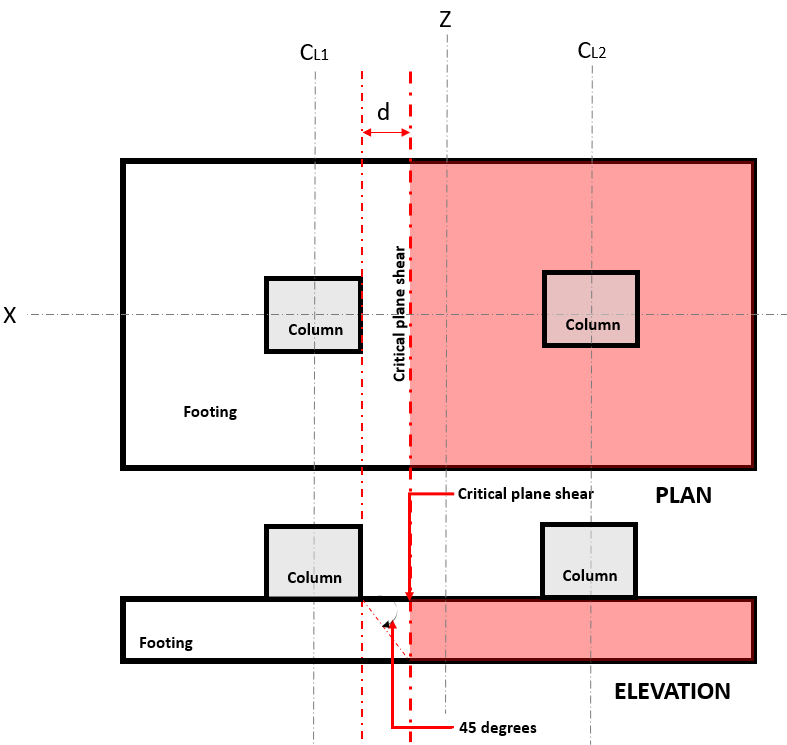
Φιγούρα 1. Κρίσιμη επίπεδη διάτμηση της μονής κατεύθυνσης

ο Μονόδρομος Κουρεύω Ζήτηση ή Β_εσύ υπολογίζεται με την προϋπόθεση ότι το πέλμα έχει προεξοχή μακριά από τη στήλη όπου βρίσκεται η περιοχή (το κόκκινο) υποδεικνύεται στο σχήμα 1 σύμφωνα με το ACI 318-14, Ενότητα 8.5.3.1.1.

ο Χωρητικότητα διάτμησης μονής κατεύθυνσης ή ϕV_ντο ορίζεται ως η τελική ισχύς διάτμησης και υπολογίζεται χρησιμοποιώντας την εξίσωση 2 ανά ACI 318-14, Ενότητα 22.5.5.1:

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = phi _{\κείμενο{κουρεύω}} \φορές 2 \τ.μ.{\κείμενο{φά'}_{\κείμενο{ντο}}} \φορές κείμενο{σι}_{\κείμενο{β}} \φορές κείμενο{ρε} \δεξί βέλος \) Εξίσωση 2 (Εξ. Εξ. 22.5.5.1 Αγγλικά)

ή

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = phi _{\κείμενο{κουρεύω}} \φορές 0.17 \τ.μ.{\κείμενο{φά'}_{\κείμενο{ντο}}} \φορές κείμενο{σι}_{\κείμενο{β}} \φορές κείμενο{ρε} \δεξί βέλος \) Εξίσωση 2 (Εξ. Εξ. 22.5.5.1 Μετρικός)

όπου:
ϕ_{κουρεύω} = συντελεστής σχεδιασμού διάτμησης
φά’_ντο = καθορισμένη αντοχή σκυροδέματος, psi ή MPa
σι_β = πάχος της βάσης, σε ή mm
d = απόσταση από ακραίες ίνες συμπίεσης έως κεντροειδές οπλισμό διαμήκους τάσης, σε ή mm

Η ζήτηση διάτμησης και η ικανότητα διάτμησης πρέπει να πληρούν την ακόλουθη εξίσωση για να πληρούν τις απαιτήσεις σχεδιασμού του ACI 318-14:

\(\κείμενο{Β}_{\κείμενο{εσύ}} \leq phi κείμενο{Β}_{\κείμενο{ντο}} \δεξί βέλος \) Εξίσωση 3 (Εξ. Εξ. 7.5.1.1(σι))

Ίδρυμα SkyCiv, σύμφωνα με την εξίσωση 3, υπολογίζει τη μονόδρομη αναλογία διατμητικής ενότητας (Εξίσωση 4) λαμβάνοντας το Shear Demand πάνω από το Shear Capacity.

\( \κείμενο{αναλογία} = frac{\κείμενο{Διατμητική ζήτηση}}{\κείμενο{Ικανότητα διάτμησης}} \δεξί βέλος \) Εξίσωση 4

Αμφίδρομη κουρά

ο Αμφίδρομη κουρά οριακή κατάσταση, γνωστός και ως “διάτμηση διάτμησης”, επεκτείνει το κρίσιμο τμήμα σε απόσταση "d / 2" από την όψη της στήλης και γύρω από την περίμετρο της στήλης. Το κρίσιμο επίπεδο διάτμησης βρίσκεται σε αυτό το τμήμα της βάσης (Ανατρέξτε στην Εικόνα 2).

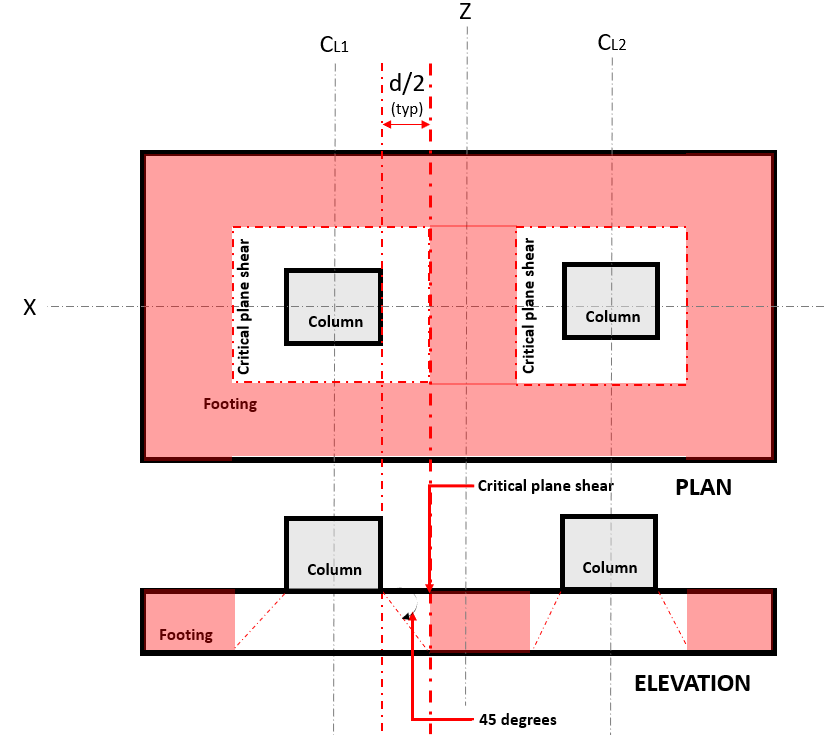
Φιγούρα 2. Κρίσιμη επίπεδη διάτμηση της αμφίδρομης διάτμησης

ο Δύο τρόποιάκου Ζήτηση ή Β_εσύ εμφανίζεται στο κρίσιμο επίπεδο διάτμησης, βρίσκεται σε απόσταση "d / 2" όπου το (το κόκκινο) εκκολαφθείσα περιοχή, υποδεικνύεται στο σχήμα 2, σύμφωνα με το ACI 318-14, Ενότητα 22.6.4.

ο Ικανότητα διάτμησης ή ϕV_ντο διέπεται από τη μικρότερη τιμή που υπολογίζεται χρησιμοποιώντας την Εξίσωση 5, 6, και 7 ανά ACI 318-14, Ενότητα 22.6.5.2:

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = phi _{\κείμενο{κουρεύω}} \φορές 4 \φορές lambda φορές sqrt{\κείμενο{φά'}_{\κείμενο{ντο}}} \δεξί βέλος \) Εξίσωση 5 (Εξ. Εξ. 22.6.5.2(ένα) Αγγλικά)

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = αριστερά ( 2 + \frac{4}{\βήτα } \σωστά ) \φορές lambda φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 6 (Εξ. Εξ. 22.6.5.2(σι) Αγγλικά)

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = αριστερά ( 2 + \frac{\άλφα _{μικρό} \φορές d }{σι{ο}} \σωστά ) \φορές lambda φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 7 (Εξ. Εξ. 22.6.5.2(ντο) Αγγλικά)

ή

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = phi _{\κείμενο{κουρεύω}} \φορές 0.33 \φορές lambda φορές sqrt{\κείμενο{φά'}_{\κείμενο{ντο}}} \δεξί βέλος \) Εξίσωση 5 (Εξ. Εξ. 22.6.5.2(ένα) Μετρικός)

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = 0.17 \φορές αριστερά ( 1 + \frac{2}{\βήτα } \σωστά ) \φορές lambda φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 6 (Εξ. Εξ. 22.6.5.2(σι) Μετρικός)

\(\phi κείμενο{Β}_{\κείμενο{ντο}} = 0.0083 \φορές αριστερά ( 2 + \frac{\άλφα _{μικρό} \φορές d }{σι{ο}} \σωστά ) \φορές lambda φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 7 (Εξ. Εξ. 22.6.5.2(ντο) Μετρικός)

Σημείωση: β είναι ο λόγος της μακράς πλευράς προς τη μικρή πλευρά της στήλης, συμπυκνωμένο φορτίο, ή περιοχή αντίδρασης και α_μικρό δίνεται 22.6.5.3

όπου:
λ = συντελεστής τροποποίησης που αντικατοπτρίζει τις μειωμένες μηχανικές ιδιότητες ελαφρού σκυροδέματος σε σχέση με το σκυρόδεμα κανονικού βάρους με την ίδια αντοχή σε θλίψη
φά’_ντο = καθορισμένη αντοχή σκυροδέματος, psi ή MPa
d = απόσταση από ακραίες ίνες συμπίεσης έως κεντροειδές οπλισμό διαμήκους τάσης, σε. ή mm

Η ζήτηση διάτμησης και η ικανότητα διάτμησης πρέπει να πληρούν την ακόλουθη εξίσωση για να πληρούν τις απαιτήσεις σχεδιασμού του ACI 318-14:

\(\κείμενο{Β}_{\κείμενο{εσύ}} \leq phi κείμενο{Β}_{\κείμενο{ντο}} \δεξί βέλος \) Εξίσωση 8 (Εξ. Εξ. 7.5.1.1(σι))

Ίδρυμα SkyCiv, σύμφωνα με την εξίσωση 8, υπολογίζει την αμφίδρομη αναλογία διατμητικής ενότητας (Εξίσωση 9) λαμβάνοντας το Shear Demand πάνω από το Shear Capacity.

\( \κείμενο{αναλογία} = frac{\κείμενο{Διατμητική ζήτηση}}{\κείμενο{Ικανότητα διάτμησης}} \δεξί βέλος \) Εξίσωση 9

Κάμψη

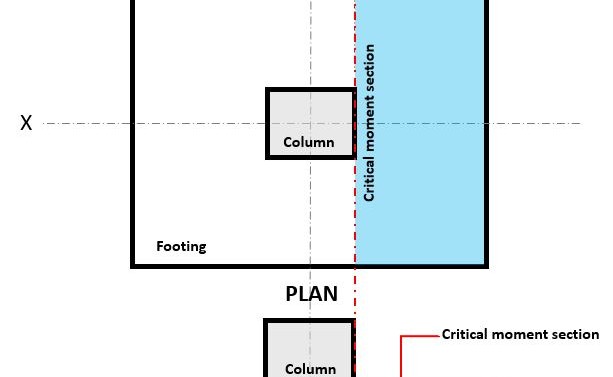
Φιγούρα 3. Τομέας κρίσιμης στιγμής του Flexure

ο Κάμψη η οριακή κατάσταση εμφανίζεται στο το τμήμα κρίσιμης κάμψης, βρίσκεται στην πρόσοψη της στήλης στην κορυφή του υποστρώματος (Ανατρέξτε στην Εικόνα 3).

ο Καμπλαστική ζήτηση, ή Μ_εσύ βρίσκεται στο τμήμα κρίσιμης κάμψης (μπλε καταπακτή) υποδεικνύεται στο σχήμα 3, και υπολογίζεται χρησιμοποιώντας την εξίσωση 10:

\( \κείμενο{Μ}_{εσύ} = κείμενο{ε}_{εσύ} \φορές αριστερά ( \frac{μεγάλο_{Χ}}{2} – \frac{ντο_{Χ}}{2} \σωστά ) \φορές l_{με} \φορές αριστερά ( \frac{\frac{μεγάλο_{Χ}}{2} – \frac{ντο_{Χ}}{2} }{2} \σωστά ) \δεξί βέλος \) Εξίσωση 10

όπου:
ε_εσύ = συντελεστής πίεσης του εδάφους, ksf ή kpa
μεγάλο_Χ = διάσταση βάσης παράλληλη προς τον άξονα x, σε ή mm
μεγάλο_με = διάσταση βάσης παράλληλη προς τον άξονα z, σε ή mm
ντο_Χ = διάσταση στήλης παράλληλα με τον άξονα x, σε ή mm

ο Κάμψη ικανότητας, ή ϕΜη υπολογίζεται χρησιμοποιώντας την εξίσωση 11:

\( \phi κείμενο{Μ}_{ν} = phi_{\κείμενο{κάμψη}} \φορές A_{μικρό} \φορές f_{και} \φορές αριστερά( ρε – \frac{ένα}{2} \σωστά) \δεξί βέλος \) Εξίσωση 11

όπου:
ϕ = συντελεστής κάμψης
μεγάλο_Χ = διάσταση βάσης παράλληλη προς τον άξονα x, σε ή mm
μεγάλο_με = διάσταση βάσης παράλληλη προς τον άξονα z, σε ή mm
d = απόσταση από ακραίες ίνες συμπίεσης έως κεντροειδές οπλισμό διαμήκους τάσης, σε ή mm
ΕΝΑ_μικρό = περιοχή ενίσχυσης, σε² ή mm²
a = βάθος ισοδύναμου ορθογώνιου μπλοκ τάσης, σε ή mm
fy = αντοχή χάλυβα, ksi ή MPa

βιβλιογραφικές αναφορές

1. Απαιτήσεις κωδικού δόμησης για δομικό σκυρόδεμα (ACI 318-14) Σχολιασμός Απαιτήσεων Κτιριακού Κώδικα για Δομικό Σκυρόδεμα (ACI 318R-14). Αμερικανικό Ινστιτούτο Σκυροδέματος, 2014.
2. ΜακΚορμάκ, Τζακ Γ., και Russell H. καφέ. Σχεδιασμός ενισχυμένου σκυροδέματος ACI 318-11 Έκδοση κώδικα. Γουίλι, 2014.
3. Τέιλορ, Ανδρέας, et αϊ. Εγχειρίδιο ενισχυμένου σκυροδέματος: ένας σύντροφος στο ACI-318-14. Αμερικανικό Ινστιτούτο Σκυροδέματος, 2015.