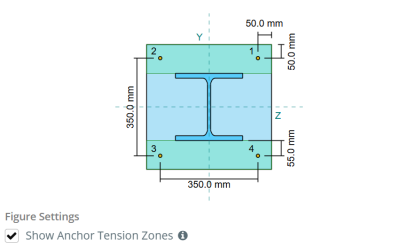
Παράδειγμα σχεδιασμού πλάκας βάσης χρησιμοποιώντας το EN 1993-1-8:2005, ΣΕ 1993-1-1:2005, ΣΕ 1992-1-1:2004, και EN 1992-4:2018.
Προβληματική δήλωση
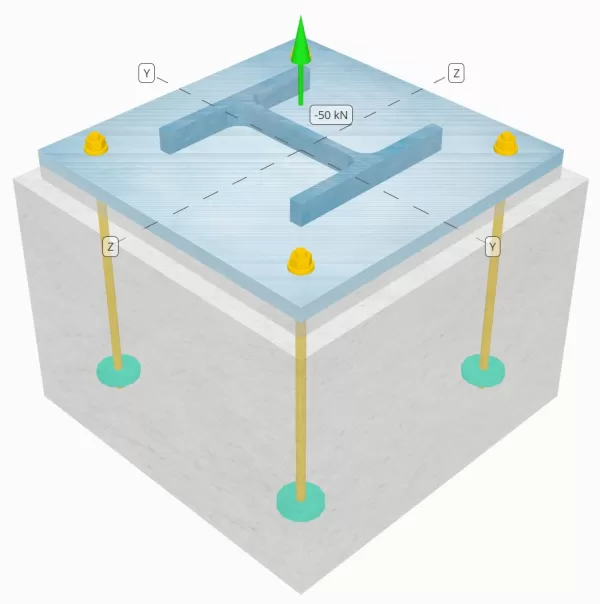
Προσδιορίστε εάν η σχεδιασμένη σύνδεση στήλης-πλάκας βάσης είναι επαρκής για φορτίο εφελκυσμού 50 kN.
Δεδομένα
Στήλη:
Ενότητα στήλης: ΑΥΤΟΣ 240 σι
Επιφάνεια στήλης: 10600 χιλ2
Υλικό στήλης: S235
Πλάκα βάσης:
Διαστάσεις πλάκας βάσης: 450 mm x 450 χιλ
Πάχος πλάκας βάσης: 20 χιλ
Υλικό πλάκας βάσης: S235
Πηκτώ:
Πάχος ενέματα: 20 χιλ
Σκυρόδεμα:
Διαστάσεις σκυροδέματος: 500 mm x 500 χιλ
Πάχος σκυροδέματος: 350 χιλ
Σκυρόδεμα: C25/30
Ραγισμένα ή αδιευκρίνιστα: Ραγισμένος
Άγκυρες:
Διάμετρος άγκυρας: 12 χιλ
Αποτελεσματικό μήκος ενσωμάτωσης: 300.0 χιλ
Διάμετρος ενσωματωμένης πλάκας: 60 χιλ
Ενσωματωμένο πάχος πλάκας: 10 χιλ
Υλικό άγκυρας: 8.8
Άλλες πληροφορίες:
- Μη βυθισμένες άγκυρες.
- Άγκυρα με κομμένες κλωστές.
Συγκολλήσεις:
Τύπος συγκόλλησης: FPBW
Η ταξινόμηση μετάλλων πλήρωσης: Ε35
Δεδομένα αγκυροβόλησης (από Υπολογιστής Skyciv):
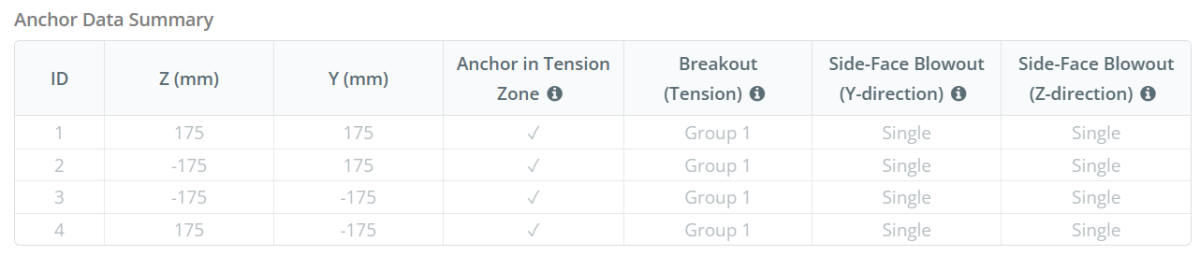
Μοντέλο στο δωρεάν εργαλείο SkyCiv
Μοντελοποιήστε το παραπάνω σχέδιο πλάκας βάσης χρησιμοποιώντας το δωρεάν διαδικτυακό μας εργαλείο σήμερα! Δεν απαιτείται εγγραφή.
Ορισμοί
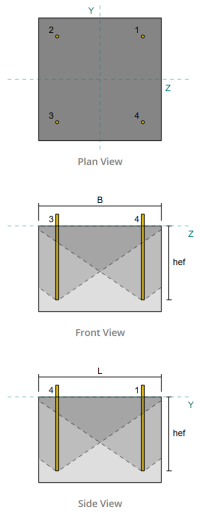
Ζώνη έντασης άγκυρας:
Στο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV, μόνο άγκυρες που βρίσκονται μέσα στο ζώνη τάσης άγκυρας θεωρούνται αποτελεσματικοί στην αντιστάθμιση της ανύψωσης. Αυτή η ζώνη περιλαμβάνει συνήθως περιοχές κοντά στις φλάντζες της στήλης ή στο διαδίκτυο. Οι άγκυρες εκτός αυτής της ζώνης δεν συμβάλλουν στην αντίσταση στην ένταση και αποκλείονται από τους υπολογισμούς ανύψωσης.
Η υπόθεση απλοποιεί την ανάλυση της πλάκας βάσης προσεγγίζοντας τον τρόπο με τον οποίο εξαπλώνεται η δύναμη ανύψωσης μέσω της πλάκας.
Ομάδες άγκυρας:
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV Περιλαμβάνει ένα διαισθητικό χαρακτηριστικό που προσδιορίζει ποιες άγκυρες αποτελούν μέρος μιας ομάδας αγκύρωσης για αξιολόγηση ξέσπασμα σκυροδέματος και έκρηξη από σκυρόδεμα στο πλάι του προσώπου αποτυχία.
Ενα ομάδα άγκυρας Αποτελείται από πολλαπλές άγκυρες με παρόμοια αποτελεσματικά βάθη ενσωμάτωσης και απόσταση, και είναι αρκετά κοντά ώστε τους Οι προβλεπόμενες περιοχές αντίστασης επικαλύπτονται. Όταν ομαδοποιούνται άγκυρες, Οι ικανότητές τους συνδυάζονται για να αντισταθούν στη συνολική δύναμη έντασης που εφαρμόζεται στην ομάδα.
Οι άγκυρες που δεν πληρούν τα κριτήρια ομαδοποίησης αντιμετωπίζονται ως άγκυρες. Σε αυτήν την περίπτωση, Μόνο η δύναμη τάσης στην ατομική άγκυρα ελέγχεται από τη δική της αποτελεσματική περιοχή αντίστασης.
Υπολογισμοί βήμα προς βήμα
Ελεγχος #1: Υπολογίστε τη χωρητικότητα συγκόλλησης
Από τις πληροφορίες που δίνονται, η συγκόλληση που χρησιμοποιείται σε αυτό το παράδειγμα σχεδίασης είναι α Πλήρης διείσδυση με άκρο συγκόλληση (FPBW). Θα υπολογίσουμε τις χωρητικότητες του βασικού μετάλλου της στήλης και της πλάκας βάσης για να προσδιορίσουμε την αντίσταση συγκόλλησης. Για να το κάνω αυτό, πρέπει πρώτα να υπολογίσουμε το Συνολικό μήκος συγκόλλησης στη στήλη και λάβετε την τάση συγκόλλησης.
\(
ΦΑ_{β,Εκδ} = frac{N_x}{2 b_f t_f + \αριστερά( ρε_{διάσελο} – 2 T_F – 2 r_{διάσελο} \σωστά) t_w}
\)
\(
ΦΑ_{β,Εκδ} = frac{50 \, \κείμενο{ΚΝ}}{2 \φορές 240 \, \κείμενο{χιλ} \φορές 17 \, \κείμενο{χιλ} + \αριστερά( 240 \, \κείμενο{χιλ} – 2 \φορές 17 \, \κείμενο{χιλ} – 2 \φορές 21 \, \κείμενο{χιλ} \σωστά) \φορές 10 \, \κείμενο{χιλ}} = 5.102 \, \κείμενο{MPa}
\)
Επόμενο, καθορίζουμε το αντοχή σε εφελκυσμό του ασθενέστερου υλικού μεταξύ της στήλης και της πλάκας βάσης.
\(
f_y = min αριστερά( φά_{και,\κείμενο{διάσελο}}, φά_{και,\κείμενο{bp}} \σωστά) = min αριστερά( 225 \, \κείμενο{MPa}, 225 \, \κείμενο{MPa} \σωστά) = 225 \, \κείμενο{MPa}
\)
Στη συνέχεια χρησιμοποιούμε ΣΕ 1993-1-8:2005 Ρήτρα 4.7.1 και ΣΕ 1993-1-1:2005 Εξ. 6.6 για τον υπολογισμό της αντίστασης συγκόλλησης σχεδιασμού FPBW.
\(
ΦΑ_{β,Rd3} = frac{f_y}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ0}} = frac{225 \, \κείμενο{MPa}}{1} = 225 \, \κείμενο{MPa}
\)
Από 5.102 MPa < 225 MPa, Η χωρητικότητα συγκόλλησης είναι επαρκής.
Ελεγχος #2: Υπολογίστε τη χωρητικότητα κάμψης πλάκας βάσης λόγω φορτίου τάσης
Για να υπολογίσετε το ικανότητα κάμψης της πλάκας βάσης έναντι του φορτίου τάσης, θα το χρησιμοποιησουμε μοτίβα γραμμής απόδοσης όπως κυκλικά σχέδια και μη κυκλικά σχέδια. Τότε, καθορίζουμε την ικανότητα διακυβέρνησης, υποθέτοντας ότι δεν υπάρχουν αδιάκριτες δυνάμεις, συγκρίνοντας την αντοχή διαρροής της πλάκας με την αντίσταση εφελκυσμού των μπουλονιών αγκύρωσης.
Υπολογίστε τις φυσικές συχνότητες της δομής σας σε Structural 3D, υπολογίζουμε τα απαιτούμενα διαστάσεις με βάση τη δεδομένη διάταξη μπουλονιών. Παραπέμπω ΣΕ 1992-1-8:2005 Τραπέζι 6.2 για καθοδήγηση.
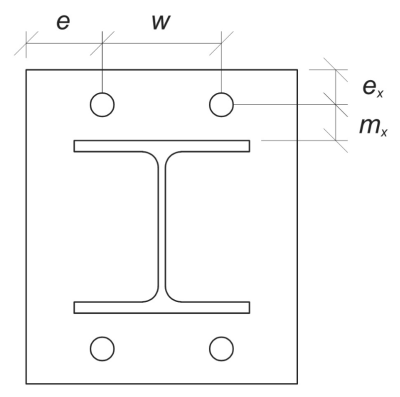
\(
m_x = frac{μικρό_ – ρε_{διάσελο}}{2} = frac{350 \, \κείμενο{χιλ} – 240 \, \κείμενο{χιλ}}{2} = 55 \, \κείμενο{χιλ}
\)
\(
w = s_z αριστερά( n_{ένα,\κείμενο{πλευρά}} – 1 \σωστά) = 350 \, \κείμενο{χιλ} \φορές αριστερά( 2 – 1 \σωστά) = 350 \, \κείμενο{χιλ}
\)
\(
e_x = frac{ΜΕΓΑΛΟ_{bp} – μικρό_}{2} = frac{450 \, \κείμενο{χιλ} – 350 \, \κείμενο{χιλ}}{2} = 50 \, \κείμενο{χιλ}
\)
\(
e = frac{ΣΙ_{bp} – β}{2} = frac{450 \, \κείμενο{χιλ} – 350 \, \κείμενο{χιλ}}{2} = 50 \, \κείμενο{χιλ}
\)
\(
b_p = B_{bp} = 450 \, \κείμενο{χιλ}
\)
Ας υπολογίσουμε επίσης την απόσταση του άκρου αγκύρωσης στην πλάκα βάσης, η οποία περιορίζεται από την \( m_x \) διάσταση ανά
\(
n = min αριστερά( πρώην, 1.25 m_x δεξιά) = min αριστερά( 50 \, \κείμενο{χιλ}, 1.25 \φορές 55 \, \κείμενο{χιλ} \σωστά) = 50 \, \κείμενο{χιλ}
\)
Τότε, υπολογίζουμε τα ενεργά μήκη των παρακάτω κυκλικά σχέδια (Συνδέσεις/Υποστήριξη Πίνακας SCI P398 5.3).
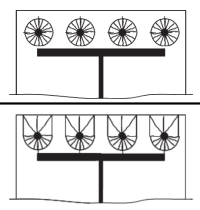
Κυκλικό σχέδιο 1:
\(
μεγάλο_{εφ,cp1} = n_{ένα,\κείμενο{πλευρά}} \pi m_x = 2 \φορές pi φορές 55 \, \κείμενο{χιλ} = 345.58 \, \κείμενο{χιλ}
\)
Κυκλικό σχέδιο 2:
\(
μεγάλο_{εφ,cp2} = αριστερά( \frac{n_{ένα,\κείμενο{πλευρά}}}{2} \σωστά) (\pi m_x + 2 πρώην) = αριστερά( \frac{2}{2} \σωστά) \φορές (\pi φορές 55 \, \κείμενο{χιλ} + 2 \φορές 50 \, \κείμενο{χιλ}) = 272.79 \, \κείμενο{χιλ}
\)
Κυβερνητικό κυκλικό σχέδιο αποτελεσματικό μήκος:
\(
μεγάλο_{εφ,cp} = min (μεγάλο_{εφ,cp1}, μεγάλο_{εφ,cp2}) = min (345.58 \, \κείμενο{χιλ}, 272.79 \, \κείμενο{χιλ}) = 272.79 \, \κείμενο{χιλ}
\)
Τώρα, υπολογίζουμε τα ενεργά μήκη των παρακάτω μη κυκλικά μοτίβα (Συνδέσεις/Υποστήριξη Πίνακας SCI P398 5.3)
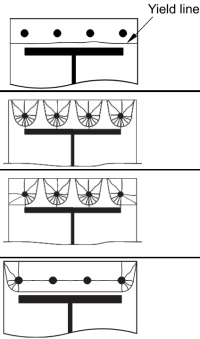
Μη κυκλικό σχέδιο 1:
\(
μεγάλο_{εφ,nc1} = frac{b_p}{2} = frac{450 \, \κείμενο{χιλ}}{2} = 225 \, \κείμενο{χιλ}
\)
Μη κυκλικό σχέδιο 2:
\(
μεγάλο_{εφ,nc2} = αριστερά( \frac{n_{ένα,\κείμενο{πλευρά}}}{2} \σωστά) (4 m_x + 1.25 πρώην) = αριστερά( \frac{2}{2} \σωστά) \φορές (4 \φορές 55 \, \κείμενο{χιλ} + 1.25 \φορές 50 \, \κείμενο{χιλ}) = 282.5 \, \κείμενο{χιλ}
\)
Μη κυκλικό σχέδιο 3:
\(
μεγάλο_{εφ,nc3} = 2 m_x + 0.625 πρώην + ε = 2 \φορές 55 \, \κείμενο{χιλ} + 0.625 \φορές 50 \, \κείμενο{χιλ} + 50 \, \κείμενο{χιλ} = 191.25 \, \κείμενο{χιλ}
\)
Μη κυκλικό σχέδιο 4:
\(
μεγάλο_{εφ,nc4} = 2 m_x + 0.625 πρώην + \frac{(n_{ένα,\κείμενο{πλευρά}} – 1) s_z}{2} = 2 \φορές 55 \, \κείμενο{χιλ} + 0.625 \φορές 50 \, \κείμενο{χιλ} + \frac{(2 – 1) \φορές 350 \, \κείμενο{χιλ}}{2} = 316.25 \, \κείμενο{χιλ}
\)
Κυβερνητικό μη κυκλικό μοτίβο αποτελεσματικό μήκος:
\(
μεγάλο_{εφ,nc} = min (μεγάλο_{εφ,nc1}, μεγάλο_{εφ,nc2}, μεγάλο_{εφ,nc3}, μεγάλο_{εφ,nc4}) = min (225 \, \κείμενο{χιλ}, 282.5 \, \κείμενο{χιλ}, 191.25 \, \κείμενο{χιλ}, 316.25 \, \κείμενο{χιλ}) = 191.25 \, \κείμενο{χιλ}
\)
Τότε, προσδιορίζουμε τη μικρότερη τιμή μεταξύ των ενεργών μηκών των κυκλικών και των μη κυκλικών σχεδίων.
\(
μεγάλο_{εφ,1} = min (μεγάλο_{εφ,cp}, μεγάλο_{εφ,nc}) = min (272.79 \, \κείμενο{χιλ}, 191.25 \, \κείμενο{χιλ}) = 191.25 \, \κείμενο{χιλ}
\)
Τώρα, Χρησιμοποιούμε αυτό το υπολογισμένο ενεργό μήκος για να υπολογίσουμε την αντίστασή του σε κάμψη. Σύμφωνα με ΣΕ 1993-1-8:2005 Τραπέζι 6.2, η αντίσταση ροπής πλάκας για λειτουργία αστοχίας 1 είναι:
\(
Μ_{παρακαλώ,1,Rd} = frac{0.25 μεγάλο_{εφ,1} (αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{bp})^2 f_{και _bp}}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ0}} = frac{0.25 \φορές 191.25 \, \κείμενο{χιλ} \φορές (20 \, \κείμενο{χιλ})^2 φορές 225 \, \κείμενο{MPa}}{1} = 4303.1 \, \κείμενο{ΚΝ} \cdot text{χιλ}
\)
Υποθέτοντας όχι αδιάκριτα, χρησιμοποιούμε ΕΝ 1993-1-8:2005 Τραπέζι 6.2 Για να προσδιορίσετε το σχέδιο αντίσταση της πλάκας βάσης για αποτυχία Λειτουργίες 1 και 2.
\(
ΦΑ_{Τ,1,Rd} = frac{2 Μ_{παρακαλώ,1,Rd}}{m_x} = frac{2 \φορές 4303.1 \, \κείμενο{ΚΝ} \cdot text{χιλ}}{55 \, \κείμενο{χιλ}} = 156.48 \, \κείμενο{ΚΝ}
\)
Τότε, υπολογίζουμε την αντίσταση εφελκυσμού της ράβδου αγκύρωσης χρησιμοποιώντας ΣΕ 1992-4:2018 Ρήτρα 7.2.1.3. Αυτό θα αναλυθεί περαιτέρω στους επόμενους ελέγχους αγκύρωσης.
\(
ΦΑ_{τ,Rd} = frac{c k_2 F_{u_anc} Οπως και}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ2, άγκυρα}} = frac{0.85 \φορές 0.9 \φορές 800 \, \κείμενο{MPa} \φορές 113.1 \, \κείμενο{χιλ}^ 2}{1.25} = 55.372 \, \κείμενο{ΚΝ}
\)
Στη συνέχεια θα χρησιμοποιήσουμε την αντίσταση ανά ράβδο αγκύρωσης για να υπολογίσουμε το αντίσταση σχεδιασμού της πλάκας βάσης υπό αποτυχία Τρόπος 3, που είναι η ολική αστοχία του μπουλονιού.
\(
ΦΑ_{Τ,3,Rd} = n_{ένα,πλευρά} ΦΑ_{τ,Rd} = 2 \φορές 55.372 \, \κείμενο{ΚΝ} = 110.74 \, \κείμενο{ΚΝ}
\)
Τελικά, προσδιορίζουμε την ισχύουσα τιμή αντίστασης μεταξύ των τρόπων αστοχίας.
\(
ΦΑ_{Τ,Rd} = min (ΦΑ_{Τ,1,Rd}, ΦΑ_{Τ,3,Rd}) = min (156.48 \, \κείμενο{ΚΝ}, 110.74 \, \κείμενο{ΚΝ}) = 110.74 \, \κείμενο{ΚΝ}
\)
Υπολογίζοντας το φορτίο τάσης ανά φλάντζα, έχουμε:
\(
ΦΑ_{Τ,Εκδ} = frac{N_x}{2} = frac{50 \, \κείμενο{ΚΝ}}{2} = 25 \, \κείμενο{ΚΝ}
\)
Από 25 ΚΝ < 110.74 ΚΝ, Η ικανότητα απόδοσης της κάμψης της πλάκας βάσης είναι επαρκής.
Ελεγχος #3: Υπολογίστε την ικανότητα εφελκυσμού της ράβδου άγκυρας
Γνωρίζουμε ήδη την τιμή για την ικανότητα εφελκυσμού της ράβδου αγκύρωσης, αλλά ας το αντιμετωπίσουμε με περισσότερες λεπτομέρειες.
Πρώτα, Ας υπολογίσουμε την περιοχή εφελκυστικής τάσης της ράβδου αγκύρωσης.
\(
A_s = frac{\πι}{4} (ρε_{Α.Κ.})^2 = frac{\πι}{4} \φορές (12 \, \κείμενο{χιλ})💕⬛ Αγορά Indocin από 113.1 \, \κείμενο{χιλ}^ 2
\)
Τότε, ας εφαρμόσουμε τις τιμές για το \( ντο \) παράγοντας και η \( κ_{2} \) παράγοντας. Αυτές οι τιμές μπορούν να τροποποιηθούν στις ρυθμίσεις του λογισμικού SkyCiv Base Plate Design. Δοκιμάστε τη δωρεάν έκδοση εδώ.
- \( γ = 0.85 \) για άγκυρες με κομμένα νήματα
- \( κ_{2} = 0.9\) για μη βυθισμένη άγκυρα
Τώρα, ας χρησιμοποιήσουμε ΣΕ 1992-4:2018 Ρήτρα 7.2.1.3 να υπολογίσει το αντίσταση σχεδιασμού της ράβδου αγκύρωσης σε ένταση.
\(
Ν_{Rd,μικρό} = frac{c k_2 F_{u_anc} Οπως και}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ2, άγκυρα}} = frac{0.85 \φορές 0.9 \φορές 800 \, \κείμενο{MPa} \φορές 113.1 \, \κείμενο{χιλ}^ 2}{1.25} = 55.372 \, \κείμενο{ΚΝ}
\)
Υπολογίζοντας το φορτίο έντασης ανά άγκυρα, έχουμε:
\(
Ν_{Εκδ} = frac{N_x}{n_{ένα,τ}} = frac{50 \, \κείμενο{ΚΝ}}{4} = 12.5 \, \κείμενο{ΚΝ}
\)
Από 12.5 ΚΝ < 55.372 ΚΝ, Η χωρητικότητα εφελκυσμού της ράβδου άγκυρας είναι επαρκής.
Ελεγχος #4: Υπολογίστε τη χωρητικότητα ξεμπλοκάρισμα από σκυρόδεμα σε ένταση

Πριν υπολογίσετε την χωρητικότητα ξεμπλοκάρισμα, πρέπει πρώτα να καθορίσουμε εάν το μέλος χαρακτηρίζεται ως στενό μέλος. Σύμφωνα με ΣΕ 1992-4:2008 Ρήτρα 7.2.1.4(8), Το μέλος πληροί τα κριτήρια για ένα στενό μέλος. Επομένως, ένα τροποποιημένος αποτελεσματικό μήκος ενσωμάτωσης πρέπει να χρησιμοποιείται στους υπολογισμούς χωρητικότητας απόσπασης. Αυτή η προσαρμογή επηρεάζει επίσης το χαρακτηριστική απόσταση και χαρακτηριστική απόσταση άκρης, η οποία πρέπει να τροποποιηθεί ανάλογα.
Με βάση τα στενά κριτήρια μελών, ο τροποποιημένες τιμές για την ομάδα άγκυρας έχουν ως εξής:
- Τροποποιημένο αποτελεσματικό μήκος ενσωμάτωσης, \( h'_{εφ} = 100 χιλ \)
- τροποποιημένη χαρακτηριστική απόσταση, \( μικρό'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το} = 300 mm)
- τροποποιημένη χαρακτηριστική απόσταση ακμών, \( ντο'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το} = 150 mm)
Χρησιμοποιώντας ΣΕ 1992-4:2018 Εξ. 7.3, υπολογίζουμε το αναφορά προβαλλόμενη περιοχή κώνου από σκυρόδεμα για μια μόνο άγκυρα.
\(
A0_{ντο,Ν} = s'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} μικρό'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} = 350 \, \κείμενο{χιλ} \φορές 350 \, \κείμενο{χιλ} = 122500 \, \κείμενο{χιλ}^ 2
\)
Ομοίως, υπολογίζουμε το Πραγματική προβλεπόμενη περιοχή κώνου σκυροδέματος της ομάδας αγκύρωσης.
\(
ΕΝΑ_{Αρ} = L_{Αρ} ΣΙ_{Αρ} = 500 \, \κείμενο{χιλ} \φορές 500 \, \κείμενο{χιλ} = 250000 \, \κείμενο{χιλ}^ 2
\)
Οπου,
\(
ΜΕΓΑΛΟ_{Αρ} = min αριστερά( ντο_{αριστερά,G1}, ντο'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} \σωστά)
+ \αριστερά( \min left( μικρό_{άθροισμα,με,G1}, μικρό'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} \αριστερά( n_{με,G1} – 1 \σωστά) \σωστά) \σωστά)
+ \min left( ντο_{σωστά,G1}, ντο'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} \σωστά)
\)
\(
ΜΕΓΑΛΟ_{Αρ} = min αριστερά( 75 \, \κείμενο{χιλ}, 175 \, \κείμενο{χιλ} \σωστά)
+ \αριστερά( \min left( 350 \, \κείμενο{χιλ}, 350 \, \κείμενο{χιλ} \φορές (2 – 1) \σωστά) \σωστά)
+ \min left( 75 \, \κείμενο{χιλ}, 175 \, \κείμενο{χιλ} \σωστά)
\)
\(
ΜΕΓΑΛΟ_{Αρ} = 500 \, \κείμενο{χιλ}
\)
\(
ΣΙ_{Αρ} = min αριστερά( ντο_{μπλουζα,G1}, ντο'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} \σωστά)
+ \αριστερά( \min left( μικρό_{άθροισμα,και,G1}, μικρό'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} \αριστερά( n_{και,G1} – 1 \σωστά) \σωστά) \σωστά)
+ \min left( ντο_{κάτω μέρος,G1}, ντο'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1} \σωστά)
\)
\(
ΣΙ_{Αρ} = min αριστερά( 75 \, \κείμενο{χιλ}, 175 \, \κείμενο{χιλ} \σωστά)
+ \αριστερά( \min left( 350 \, \κείμενο{χιλ}, 350 \, \κείμενο{χιλ} \φορές (2 – 1) \σωστά) \σωστά)
+ \min left( 75 \, \κείμενο{χιλ}, 175 \, \κείμενο{χιλ} \σωστά)
\)
\(
ΣΙ_{Αρ} = 500 \, \κείμενο{χιλ}
\)
Επόμενο, Αξιολογούμε το χαρακτηριστική δύναμη μιας μόνο άγκυρας που χρησιμοποιεί ΣΕ 1992-4:2018 Εξ. 7.2
\(
N0_{Rk,ντο} = k_1 sqrt{\frac{φά_{ck}}{\κείμενο{MPa}}} \αριστερά( \frac{h'_{εφ,G1}}{\κείμενο{χιλ}} \σωστά)^{1.5} Ν
\)
\(
N0_{Rk,ντο} = 8.9 \φορές sqrt{\frac{25 \, \κείμενο{MPa}}{1 \, \κείμενο{MPa}}} \φορές αριστερά( \frac{116.67 \, \κείμενο{χιλ}}{1 \, \κείμενο{χιλ}} \σωστά)^{1.5} \φορές 0.001 \, \κείμενο{ΚΝ} = 56.076 \, \κείμενο{ΚΝ}
\)
Οπου,
- \(κ_{1} = 8.9\) για άγκυρες
Τώρα, αξιολογούμε τα αποτελέσματα της γεωμετρίας υπολογίζοντας τα απαραίτητα Παράμετροι για αντοχή σε διάσπαση.
Η συντομότερη απόσταση ακμής της ομάδας αγκύρωσης καθορίζεται ως:
\(
ντο_{ελάχ,Ν} = min αριστερά( ντο_{αριστερά,G1}, ντο_{σωστά,G1}, ντο_{μπλουζα,G1}, ντο_{κάτω μέρος,G1} \σωστά)
= min αριστερά( 87.5 \, \κείμενο{χιλ}, 87.5 \, \κείμενο{χιλ}, 150 \, \κείμενο{χιλ}, 150 \, \κείμενο{χιλ} \σωστά)
= 87.5 \, \κείμενο{χιλ}
\)
Σύμφωνα με ΣΕ 1992-4:2018 Εξ. 7.4, η τιμή για την παράμετρο που υπολογίζει την κατανομή της τάσης στο σκυρόδεμα είναι:
\(
\Psi_{μικρό,Ν} = min αριστερά( 0.7 + 0.3 \αριστερά( \frac{ντο_{ελάχ,Ν}}{ντο'_{Ενώ το Restraint θα απαιτήσει να εισαγάγετε το,G1}} \σωστά), 1.0 \σωστά)
= min αριστερά( 0.7 + 0.3 \φορές αριστερά( \frac{75 \, \κείμενο{χιλ}}{175 \, \κείμενο{χιλ}} \σωστά), 1 \σωστά)
= 0.82857
\)
ο εφέ απολέπισης του κελύφους λογίζεται για χρήση ΣΕ 1992-4:2018 Εξ. 7.5, χορήγηση:
\(
\Psi_{σχετικά με,Ν} = min αριστερά( 0.5 + \frac{h'_{εφ,G1}}{\κείμενο{χιλ} \, / \, 200}, 1.0 \σωστά)
= min αριστερά( 0.5 + \frac{116.67 \, \κείμενο{χιλ}}{1 \, \κείμενο{χιλ} \, / \, 200}, 1 \σωστά)
= 1
\)
Επιπλέον, και οι δύο παράγοντας εκκεντρότητας και το παράγοντας επιρροής συμπίεσης λαμβάνονται ως:
\(
\Psi_{εκ,Ν} = 1
\)
\(
\Psi_{Μ,Ν} = 1
\)
Στη συνέχεια συνδυάζουμε όλους αυτούς τους παράγοντες και εφαρμόζουμε ΟΠΩΣ ΚΑΙ 5216:2021 Εξίσωση 6.2.3.1 Για να αξιολογήσετε το σχεδίαση αντοχής σε διάσπαση κώνου σκυροδέματος για την ομάδα άγκυρας:
\(
Ν_{Rd,ντο} = frac{N0_{Rk,ντο} \αριστερά( \frac{ΕΝΑ_{Αρ}}{A0_{ντο,Ν}} \σωστά) \Psi_{μικρό,Ν} \Psi_{σχετικά με,Ν} \Psi_{εκ,Ν} \Psi_{Μ,Ν}}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Mc}}
\)
\(
Ν_{Rd,ντο} = frac{56.076 \, \κείμενο{ΚΝ} \φορές αριστερά( \frac{250000 \, \κείμενο{χιλ}^ 2}{122500 \, \κείμενο{χιλ}^ 2} \σωστά) \φορές 0.82857 \φορές 1 \φορές 1 \φορές 1}{1.5} = 63.215 \, \κείμενο{ΚΝ}
\)
ο Συνολικό φορτίο εφαρμοζόμενης τάσης στην ομάδα αγκύρωσης υπολογίζεται πολλαπλασιάζοντας το φορτίο τάσης ανά άγκυρα με τον αριθμό των αγκυρίων:
\(
Ν_{φά} = αριστερά( \frac{N_x}{n_{ένα,τ}} \σωστά) n_{ένα,G1} = αριστερά( \frac{50 \, \κείμενο{ΚΝ}}{4} \σωστά) \φορές 4 = 50 \, \κείμενο{ΚΝ}
\)
Από 50 ΚΝ < 63.215 ΚΝ Η χωρητικότητα ξεμπλοκάρισμα του σκυροδέματος είναι επαρκής.
Ελεγχος #5: Υπολογίστε την χωρητικότητα αγκύρωσης
ο ικανότητα έλξης μιας άγκυρας διέπεται από την αντίσταση στο ενσωματωμένο άκρο της. Να ξεκινήσω, υπολογίζουμε το επιφάνεια έδρας της ενσωματωμένης πλάκας, που είναι η καθαρή περιοχή μετά την αφαίρεση της περιοχής που καταλαμβάνεται από τη ράβδο αγκύρωσης.
Πρώτα, Υπολογίζουμε τη μέγιστη διάσταση της κεφαλής αγκύρωσης που είναι αποτελεσματική για την αντίσταση έλξης, σύμφωνα με ΣΕ 1992-4:2018 Ρήτρα 7.2.1.5 Σημείωση.
\(
ρε_{η,\κείμενο{Μέγιστη}} = min αριστερά( αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{\κείμενο{ενσωματωμένος _plate}}, 6 \αριστερά( αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{\κείμενο{ενσωματωμένος _plate}} \σωστά) + ρε_{\κείμενο{Α.Κ.}} \σωστά)
= min αριστερά( 60 \, \κείμενο{χιλ}, 6 \φορές (10 \, \κείμενο{χιλ}) + 12 \, \κείμενο{χιλ} \σωστά)
= 60 \, \κείμενο{χιλ}
\)
Επόμενο, υπολογίζουμε την καθαρή επιφάνεια έδρασης της κυκλικής ενσωματωμένης πλάκας χρησιμοποιώντας:
\(
ΕΝΑ_{brg} = frac{\πι}{4} \αριστερά( \αριστερά( ρε_{η,\κείμενο{Μέγιστη}} \σωστά)^ 2 – \αριστερά( ρε_{\κείμενο{Α.Κ.}} \σωστά)^2 right)
\)
\(
ΕΝΑ_{brg} = frac{\πι}{4} \φορές αριστερά( \αριστερά( 60 \, \κείμενο{χιλ} \σωστά)^ 2 – \αριστερά( 12 \, \κείμενο{χιλ} \σωστά)^2 right) = 2714.3 \, \κείμενο{χιλ}^ 2
\)
Στη συνέχεια υπολογίζουμε το αντίσταση έλξης σκυροδέματος σχεδιασμού της χυτής άγκυρας σε εφελκυσμό χρησιμοποιώντας ΣΕ 1992-4:2018 Ρήτρα 7.2.1.5:
\(
Ν_{Rd,μικρό} = frac{k_2 A_{brg} φά_{ck}}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Mp}}
= frac{7.5 \φορές 2714.3 \, \κείμενο{χιλ}^2 φορές 25 \, \κείμενο{MPa}}{1.5}
= 339.29 \, \κείμενο{ΚΝ}
\)
Θυμηθείτε τους προηγουμένως υπολογισμένους φορτίο έντασης ανά άγκυρα:
\(
Ν_{Εκδ} = frac{N_x}{n_{ένα,τ}} = frac{50 \, \κείμενο{ΚΝ}}{4} = 12.5 \, \κείμενο{ΚΝ}
\)
Από 12.5 ΚΝ < 339.29 ΚΝ, η χωρητικότητα αγκύρωσης είναι επαρκής.
Ελεγχος #6: Υπολογίστε την χωρητικότητα εκτόξευσης πλευρικού προσώπου σε κατεύθυνση y

Ας εξετάσουμε το Anchor ID #3. Ξεκινάμε υπολογίζοντας την απόσταση της ακμής από το άκρη αστοχίας.
\(
ντο_{με,\κείμενο{ελάχ}} = min αριστερά( ντο_{\κείμενο{αριστερά,s3}}, ντο_{\κείμενο{σωστά,s3}} \σωστά)
= min αριστερά( 75 \, \κείμενο{χιλ}, 425 \, \κείμενο{χιλ} \σωστά)
= 75 \, \κείμενο{χιλ}
\)
Επόμενο, καθορίζουμε την απόσταση ακμής προς το ορθογώνιο άκρο.
\(
ντο_{και,\κείμενο{ελάχ}} = min αριστερά( ντο_{\κείμενο{μπλουζα,s3}}, ντο_{\κείμενο{κάτω μέρος,s3}} \σωστά)
= min αριστερά( 425 \, \κείμενο{χιλ}, 75 \, \κείμενο{χιλ} \σωστά)
= 75 \, \κείμενο{χιλ}
\)
Χρησιμοποιώντας ΣΕ 1992-4:2018 Εξ. 7.27, ας υπολογίσουμε το προβλεπόμενη περιοχή αναφοράς ενός μόνο συνδετήρα.
\(
A0_{ντο,Σημ} = αριστερά( 4 ντο_{με,\κείμενο{ελάχ}} \σωστά)^ 2
= αριστερά( 4 \φορές 75 \, \κείμενο{χιλ} \σωστά)^ 2
= 90000 \, \κείμενο{χιλ}^ 2
\)
Δεδομένου ότι ελέγχουμε τη χωρητικότητα της ομάδας αγκύρωσης, ας πάρουμε το πραγματική προβλεπόμενη περιοχή της ομάδας αγκύρωσης χρησιμοποιώντας ΣΕ 1992-4:2018 Εξ. 7.27.
\(
ΕΝΑ_{Αρ} = B_{ντο,Σημ} η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{ντο,Σημ} = 225 \, \κείμενο{χιλ} \φορές 200 \, \κείμενο{χιλ} = 45000 \, \κείμενο{χιλ}^ 2
\)
Οπου,
\(
ΣΙ_{ντο,Σημ} = 2 ντο_{με,\κείμενο{ελάχ}} + \min left( 2 ντο_{με,\κείμενο{ελάχ}}, ντο_{και,\κείμενο{ελάχ}} \σωστά)
= 2 \φορές 75 \, \κείμενο{χιλ} + \min left( 2 \φορές 75 \, \κείμενο{χιλ}, 75 \, \κείμενο{χιλ} \σωστά)
= 225 \, \κείμενο{χιλ}
\)
\(
η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{ντο,Σημ} = 2 ντο_{με,\κείμενο{ελάχ}} + \αριστερά( \min left( αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{\κείμενο{σύμπλεγμα}} – ω_{\κείμενο{εφ}}, 2 ντο_{με,\κείμενο{ελάχ}} \σωστά) \σωστά)
= 2 \φορές 75 \, \κείμενο{χιλ} + \αριστερά( \min left( 350 \, \κείμενο{χιλ} – 300 \, \κείμενο{χιλ}, 2 \φορές 75 \, \κείμενο{χιλ} \σωστά) \σωστά)
= 200 \, \κείμενο{χιλ}
\)
Στον υπολογισμό του χαρακτηριστική αντοχή σε εκτόξευση σκυροδέματος μιας μεμονωμένης άγκυρας, θα το χρησιμοποιησουμε ΣΕ 1992-4:2018 Εξ. 7.26.
\(
N0_{Rk,γβ} = k_5 αριστερά( \frac{ντο_{με,\κείμενο{ελάχ}}}{\κείμενο{χιλ}} \σωστά)
\αριστερά( \τ.μ.{\frac{ΕΝΑ_{\κείμενο{brg}}}{\κείμενο{χιλ}^ 2}} \σωστά)
\αριστερά( \τ.μ.{\frac{φά_{ck}}{\κείμενο{MPa}}} \σωστά) Ν
\)
\(
N0_{Rk,γβ} = 8.7 \φορές αριστερά( \frac{75 \, \κείμενο{χιλ}}{1 \, \κείμενο{χιλ}} \σωστά)
\φορές αριστερά( \τ.μ.{\frac{2714.3 \, \κείμενο{χιλ}^ 2}{1 \, \κείμενο{χιλ}^ 2}} \σωστά)
\φορές αριστερά( \τ.μ.{\frac{25 \, \κείμενο{MPa}}{1 \, \κείμενο{MPa}}} \σωστά)
\φορές 0.001 \, \κείμενο{ΚΝ}
\)
\(
N0_{Rk,γβ} = 169.97 \, \κείμενο{ΚΝ}
\)
Τότε, θα πάρουμε το παραμέτρους εξάτμισης πλευρικού προσώπου.
Η παράμετρος που υπολογίζει τη διαταραχή της κατανομής των τάσεων στο σκυρόδεμα μπορεί να υπολογιστεί από ΣΕ 1992-4:2018 Εξ. 7.28.
\(
\Psi_{μικρό,Σημ} = min αριστερά( 0.7 + 0.3 \αριστερά( \frac{ντο_{και,\κείμενο{ελάχ}}}{2 ντο_{με,\κείμενο{ελάχ}}} \σωστά), 1.0 \σωστά)
= min αριστερά( 0.7 + 0.3 \φορές αριστερά( \frac{75 \, \κείμενο{χιλ}}{2 \φορές 75 \, \κείμενο{χιλ}} \σωστά), 1 \σωστά)
= 0.85
\)
Επιπλέον, οι παράγοντες για την επίδραση της ομάδας και ο παράγοντας της επιρροής της εκκεντρικότητας είναι οι εξής:
\(
\Psi_{σολ,Σημ} = 1
\)
\(
\Psi_{εκ,Ν} = 1
\)
Τελικά, σε αναφορά σε ΟΠΩΣ ΚΑΙ 5216:2021 Εξ. 6.2.7 για ράβδους αγκύρωσης με κεφαλή, ο σχεδίαση αντίστασης εκτόξευσης σκυροδέματος είναι:
\(
Ν_{Rk,γβ} = frac{N0_{Rk,γβ} \αριστερά( \frac{ΕΝΑ_{Αρ}}{A0_{ντο,Σημ}} \σωστά) \αριστερά( \Psi_{μικρό,Σημ} \σωστά) \αριστερά( \Psi_{σολ,Σημ} \σωστά) \αριστερά( \Psi_{εκ,Ν} \σωστά)}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Mc}}
\)
\(
Ν_{Rk,γβ} = frac{169.97 \, \κείμενο{ΚΝ} \φορές αριστερά( \frac{45000 \, \κείμενο{χιλ}^ 2}{90000 \, \κείμενο{χιλ}^ 2} \σωστά) \φορές αριστερά( 0.85 \σωστά) \φορές αριστερά( 1 \σωστά) \φορές αριστερά( 1 \σωστά)}{1.5} = 48.159 \, \κείμενο{ΚΝ}
\)
Ανάκληση φορτίο έντασης ανά άγκυρα:
\(
Ν_{Εκδ} = frac{N_x}{n_{ένα,τ}} = frac{50 \, \κείμενο{ΚΝ}}{4} = 12.5 \, \κείμενο{ΚΝ}
\)
Από 12.5 ΚΝ < 48.159 ΚΝ, η έκρηξη πλευρικής όψης σκυροδέματος κατά μήκος της κατεύθυνσης Υ είναι επαρκής.
Μπορεί επίσης να χρησιμοποιηθεί οποιοσδήποτε άλλος αριθμός αναγνώρισης Anchor και θα έχει το ίδιο αποτέλεσμα, αφού το σχέδιο είναι συμμετρικό.
Ελεγχος #7: Υπολογίστε την χωρητικότητα εκτόξευσης πλευρικού προσώπου στην κατεύθυνση z

Η ίδια διαδικασία χρησιμοποιείται για τον υπολογισμό της χωρητικότητας για εκρήξεις πλευρικής όψης στην κατεύθυνση Z. Ας εξετάσουμε το Anchor ID #2 αυτή τη φορά. Πάλι, ξεκινάμε υπολογίζοντας την απόσταση της ακμής προς το άκρη αστοχίας.
\(
ντο_{και,\κείμενο{ελάχ}} = min αριστερά( ντο_{\κείμενο{μπλουζα},δ2}, ντο_{\κείμενο{κάτω μέρος},δ2} \σωστά)
= min αριστερά( 75 \, \κείμενο{χιλ}, 425 \, \κείμενο{χιλ} \σωστά)
= 75 \, \κείμενο{χιλ}
\)
Επόμενο, καθορίζουμε την απόσταση ακμής προς το ορθογώνιο άκρο.
\(
ντο_{με,\κείμενο{ελάχ}} = min αριστερά( ντο_{\κείμενο{αριστερά},δ2}, ντο_{\κείμενο{σωστά},δ2} \σωστά)
= min αριστερά( 75 \, \κείμενο{χιλ}, 425 \, \κείμενο{χιλ} \σωστά)
= 75 \, \κείμενο{χιλ}
\)
Χρησιμοποιώντας ΣΕ 1992-4:2018 Εξ. 7.27, ας υπολογίσουμε το προβλεπόμενη περιοχή αναφοράς ενός μόνο συνδετήρα.
\(
A0_{ντο,Σημ} = αριστερά( 4 ντο_{και,\κείμενο{ελάχ}} \σωστά)^ 2
= αριστερά( 4 \φορές 75 \, \κείμενο{χιλ} \σωστά)^ 2
= 90000 \, \κείμενο{χιλ}^ 2
\)
Δεδομένου ότι ελέγχουμε τη χωρητικότητα της ομάδας αγκύρωσης, ας πάρουμε το πραγματική προβλεπόμενη περιοχή της ομάδας αγκύρωσης χρησιμοποιώντας ΣΕ 1992-4:2018 Εξ. 7.27.
\(
ΕΝΑ_{Αρ} = B_{ντο,Σημ} η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{ντο,Σημ}
= 225 \, \κείμενο{χιλ} \φορές 200 \, \κείμενο{χιλ}
= 45000 \, \κείμενο{χιλ}^ 2
\)
Οπου,
\(
ΣΙ_{ντο,Σημ} = 2 ντο_{και,\κείμενο{ελάχ}} + \min left( 2 ντο_{και,\κείμενο{ελάχ}}, ντο_{με,\κείμενο{ελάχ}} \σωστά)
= 2 \φορές 75 \, \κείμενο{χιλ} + \min left( 2 \φορές 75 \, \κείμενο{χιλ}, 75 \, \κείμενο{χιλ} \σωστά)
= 225 \, \κείμενο{χιλ}
\)
\(
η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{ντο,Σημ} = 2 ντο_{και,\κείμενο{ελάχ}} + \αριστερά( \min left( αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{\κείμενο{σύμπλεγμα}} – ω_{\κείμενο{εφ}}, 2 ντο_{και,\κείμενο{ελάχ}} \σωστά) \σωστά)
= 2 \φορές 75 \, \κείμενο{χιλ} + \αριστερά( \min left( 350 \, \κείμενο{χιλ} – 300 \, \κείμενο{χιλ}, 2 \φορές 75 \, \κείμενο{χιλ} \σωστά) \σωστά)
= 200 \, \κείμενο{χιλ}
\)
Στον υπολογισμό του χαρακτηριστική αντοχή σε εκτόξευση σκυροδέματος μιας μεμονωμένης άγκυρας, θα το χρησιμοποιησουμε ΣΕ 1992-4:2018 Εξ. 7.26.
\(
N0_{Rk,γβ} = k_5 αριστερά( \frac{ντο_{και,\κείμενο{ελάχ}}}{\κείμενο{χιλ}} \σωστά)
\τ.μ.{\αριστερά( \frac{ΕΝΑ_{brg}}{\κείμενο{χιλ}^ 2} \σωστά)}
\τ.μ.{\αριστερά( \frac{φά_{ck}}{\κείμενο{MPa}} \σωστά)} \, \κείμενο{Ν}
\)
\(
N0_{Rk,γβ} = 8.7 \αριστερά( \frac{75 \, \κείμενο{χιλ}}{1 \, \κείμενο{χιλ}} \σωστά)
\τ.μ.{\αριστερά( \frac{2714.3 \, \κείμενο{χιλ}^ 2}{1 \, \κείμενο{χιλ}^ 2} \σωστά)}
\τ.μ.{\αριστερά( \frac{25 \, \κείμενο{MPa}}{1 \, \κείμενο{MPa}} \σωστά)}
\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης 0.001 \, \κείμενο{ΚΝ}
\)
\(
N0_{Rk,γβ} = 169.97 \, \κείμενο{ΚΝ}
\)
Τότε, θα πάρουμε το παραμέτρους εξάτμισης πλευρικού προσώπου.
Η παράμετρος που υπολογίζει τη διαταραχή της κατανομής των τάσεων στο σκυρόδεμα μπορεί να υπολογιστεί από ΣΕ 1992-4:2018 Εξ. 7.28.
\(
\Psi_{μικρό,Σημ} = min αριστερά( 0.7 + 0.3 \αριστερά( \frac{ντο_{με,\κείμενο{ελάχ}}}{2 ντο_{και,\κείμενο{ελάχ}}} \σωστά), 1.0 \σωστά)
= min αριστερά( 0.7 + 0.3 \φορές αριστερά( \frac{75 \, \κείμενο{χιλ}}{2 \φορές 75 \, \κείμενο{χιλ}} \σωστά), 1 \σωστά)
= 0.85
\)
Επιπλέον, οι παράγοντες για την επίδραση της ομάδας και ο παράγοντας της επιρροής της εκκεντρικότητας είναι οι εξής:
\(
\Psi_{σολ,Σημ} = 1
\)
\(
\Psi_{εκ,Ν} = 1
\)
Τελικά, σε αναφορά σε ΟΠΩΣ ΚΑΙ 5216:2021 Εξ. 6.2.7 για ράβδους αγκύρωσης με κεφαλή, ο σχεδίαση αντίστασης εκτόξευσης σκυροδέματος είναι:
Ανάκληση φορτίο έντασης ανά άγκυρα:
\(
Ν_{Εκδ} = frac{N_x}{n_{ένα,τ}} = frac{50 \, \κείμενο{ΚΝ}}{4} = 12.5 \, \κείμενο{ΚΝ}
\)
Από 12.5 ΚΝ < 48.159 ΚΝ, η εκτόξευση πλευρικής όψης σκυροδέματος κατά μήκος της κατεύθυνσης Z είναι επαρκής.
Μπορεί επίσης να χρησιμοποιηθεί οποιοσδήποτε άλλος αριθμός αναγνώρισης Anchor και θα έχει το ίδιο αποτέλεσμα, αφού το σχέδιο είναι συμμετρικό.
Περίληψη σχεδίου
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV Μπορεί να δημιουργήσει αυτόματα μια αναφορά υπολογισμού βήμα προς βήμα για αυτό το παράδειγμα σχεδιασμού. Παρέχει επίσης μια περίληψη των επιταγών που εκτελούνται και των προκύπτουσων αναλογιών τους, καθιστώντας τις πληροφορίες κατανοητές με μια ματιά. Παρακάτω είναι ένας πίνακας συνοπτικών δείγματος, που περιλαμβάνεται στην αναφορά.
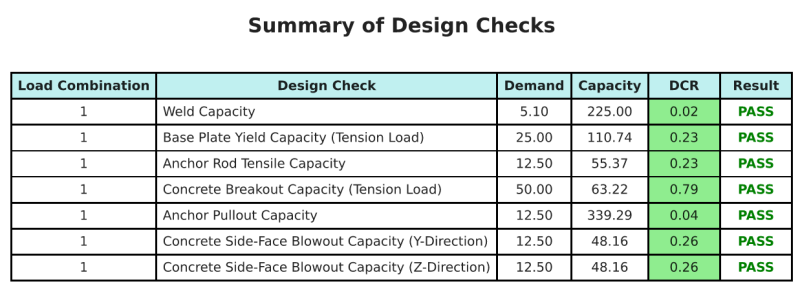
Αναφορά δείγματος SkyCIV
Δείτε το επίπεδο λεπτομέρειας και σαφήνειας που μπορείτε να περιμένετε από μια αναφορά σχεδίασης πλάκας βάσης SkyCiv. Η αναφορά περιλαμβάνει όλους τους βασικούς ελέγχους σχεδιασμού, εξισώσεις, και τα αποτελέσματα παρουσιάζονται σε σαφή και ευανάγνωστη μορφή. Είναι πλήρως συμβατό με τα πρότυπα σχεδιασμού. Κάντε κλικ παρακάτω για να προβάλετε ένα δείγμα αναφοράς που δημιουργήθηκε με χρήση του SkyCiv Base Plate Calculator.
Αγορά λογισμικού πλάκας βάσης
Αγοράστε την πλήρη έκδοση της μονάδας σχεδιασμού πλάκας βάσης από μόνη της χωρίς άλλες ενότητες SkyCIV. Αυτό σας δίνει ένα πλήρες σύνολο αποτελεσμάτων για σχεδιασμό πλάκας βάσης, συμπεριλαμβανομένων λεπτομερών αναφορών και περισσότερων λειτουργιών.