Definizione di analisi di frequenza?
Quando si progettano edifici, ci sono due tipi di carichi considerare: statico e dinamico. Per il primo, è solo necessario calcolare la risposta diretta della struttura ai carichi permanenti applicati in termini di spostamento e sollecitazioni. Questo può essere ottenuto usando il metodo Rigidità o Elementi Finiti.
Nel caso dell'analisi dinamica, è più impegnativo considerare la gamma di possibili variazioni nella risposta della struttura a causa dei carichi dipendenti dal tempo. Pertanto, alcuni nuovi strumenti o funzioni diventano essenziali da includere nell'analisi. Quindi, analisi di frequenza, un metodo fondamentale nella meccanica delle vibrazioni, sorge.
Questo metodo ottiene la variazione nel tempo del moto della struttura dovuto ai carichi dinamici applicati. Più specificamente, ciò implica utilizzare le proprietà naturali di vibrazione del sistema strutturale per calcolare le forze interne, spostamenti, problemi di stabilità, eccetera.
Per ulteriori informazioni sull'argomento, suggeriamo di leggere un articolo SkyCiv che spiega brevemente come eseguire a Analisi di frequenza dinamica usando Software di analisi strutturale SkyCiv.
Perché l'analisi della frequenza è rilevante per la progettazione?
Il modo migliore per misurare l'importanza dell'analisi della frequenza in un progetto è osservare il caso di alcune strutture che si sono guastate a causa di un cattivo comportamento dinamico. Un famoso ponte in Nord America è il Tacoma Narrows, che alla fine crollò dopo vibrazioni periodiche sostenute dal vento. Le immagini seguenti mostreranno l'aumento dello spostamento lungo il ponte appena prima del crollo, principalmente incentrato sulla carreggiata:

Figura i. Vibrazioni torsionali laterali nel Tacoma Narrows Bridge

Figura ii. Aumento dello spostamento sul ponte prima del crollo.

Figura iii. Crollo catastrofico del ponte
In questo caso di studio, non è stata eseguita una corretta analisi della frequenza e la struttura non è stata adeguatamente progettata per considerare la frequenza naturale della struttura.
Pendolo semplice
L'analisi della frequenza studia le diverse forme che una struttura sviluppa quando è soggetta ad azioni dinamiche esterne. Questo è il motivo per cui ne ottieni diversi modalità. Quindi utilizzare questi moduli, possiamo stabilire le dimensioni degli elementi della struttura attraverso le forze interne necessarie a garantire l'equilibrio.
Prima di approfondire considerazioni tecniche e matematiche per l'analisi della frequenza, rivedere il prossimo sistema semplice di una colonna a pendolo mostrato in figura iv.
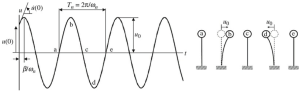
Figura iv. La risposta dinamica di un sistema a pendolo a vibrazione libera
Utilizzando una semplice analisi come indicato nell'ultima immagine, possiamo definire ogni volta il movimento della massa superiore per la colonna del pendolo. L'obiettivo principale di questo articolo sarà quello di coprire l'analisi della frequenza per due casi tipici, gradi di libertà singoli e multipli.
Un solo grado di libertà
Questo caso particolare è il più semplice per l'analisi dinamica. Il comportamento è descritto utilizzando la legge di equilibrio di D'Alembert, un'estensione della seconda legge di Newton.
La figura seguente mostra gli elementi del sistema SDOF, rigidità (K), smorzamento (c), e fonte di massa (m) per le forze d'inerzia. La forza esterna variabile nel tempo applicata sulla massa è rappresentata da \({p(t)}\).
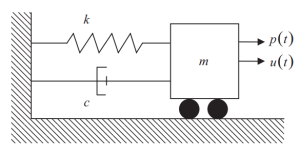
figura 1. Un solo grado di libertà (SDOF) Sistema. (Ciotola, 2017, . 56)
Tutti gli elementi devono soddisfare la condizione di equilibrio dinamico:
\({m}{\punto{u}}+{c}{\punto{u}}+{K}{u}={p(t)}\)
Questa è un'equazione differenziale lineare del secondo ordine, e la sua soluzione ha due componenti:
\({u(t)}={u}_{h}(t)+{u}_{p}(t)\)
Dove:
- \({u(t)}\) è lo spostamento assoluto.
- \({u}_{h}(t)\) è la soluzione omogenea, generalmente coinvolgendo la cassa di vibrazione libera.
- \({u}_{p}(t)\) è la soluzione particolare in base all'eccitazione applicata.
Ci concentreremo solo sulla soluzione omogenea per descrivere il comportamento vibrazionale e le caratteristiche dinamiche più critiche che una struttura ha.
Definiamo i seguenti termini:
\({\Eurocodice di design con piastra di base in acciaio{n}}={\sqrt(\frac {K}{m})}\) Frequenza angolare
\({\xi}={\frac{c}{{2}{m}{\omega_n}}}={\frac{c}{{2}{\sqrt(\frac {K}{m})}}}\) Frazione di smorzamento critico
Quando la frazione di smorzamento critico è inferiore a 1, la cassa delle vibrazioni sarà smorzata; questo è, ci saranno cicli completati prima che il movimento si fermi.
La soluzione è della seguente forma generale
\({u_h}={e^{{-\xi}{\Eurocodice di design con piastra di base in acciaio{n}}{t}}}{[{A}{cos}{\omega_d}{t}+{B}{senza}{\omega_d}{t}]}\)
Dove:
- A e B sono costanti di integrazione che dipendono dalle condizioni iniziali del moto.
- \({\omega_d}={\omega_n}{\sqrt({{1}-{\xi^2}})}\) è la frequenza angolare smorzata
Una volta valutate le costanti A e B, la soluzione generale per il caso non smorzato è
\({u_h}={e^{{-\xi}{\Eurocodice di design con piastra di base in acciaio{n}}{t}}}{[{u_0}{cos}{\omega_d}{t}+{\frac{{\punto{u_0}}+{\xi}{\omega_n}{u_0}}{\omega_d}}{senza}{\omega_d}{t}]}\)
Dove:
- \({u_0}\) è lo spostamento iniziale della massa
- \(\punto{u_0}\) è la velocità iniziale della massa
Se tracciamo la soluzione con alcuni valori delle condizioni iniziali, otterremo la figura seguente.
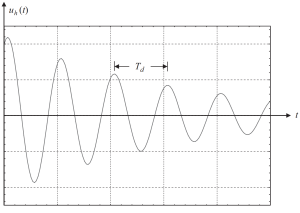
figura 2. Lo spostamento si traduce in una parte omogenea della soluzione in un caso smorzato subcritico. (Ciotola, 2017, . 58)
Nell'altro caso, è fondamentale analizzare cosa succede quando la frazione di smorzamento critico ha un valore di 1. \({\xi}=1). Questa condizione implica una struttura con smorzamento completo.
L'equazione da usare è
\({u_h}={e^{{-\Eurocodice di design con piastra di base in acciaio{n}}{t}}}{\{u_0+({\punto{u_0}}+{\omega_n}{u_0}){t}}\}\)
E il loro grafico che mostra diversi casi di condizioni iniziali è nell'immagine seguente.
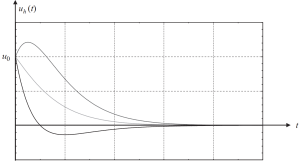
figura 3. Lo spostamento si traduce in una parte omogenea della soluzione in un caso smorzato in modo critico. (Ciotola, 2017, . 58)
Parametri di risposta
La sezione precedente ci ha aiutato a definire la soluzione per la vibrazione dinamica libera in un sistema SDOF. I due parametri principali sono la frequenza naturale \(\omega_n\) che indica come la struttura vibrerà da sola, e la frazione di smorzamento critico \(\xi\), che definisce la velocità nel decadimento delle vibrazioni.
Generalmente, le strutture hanno un basso smorzamento con un valore massimo di \(\xi\)=10 %. Se valutiamo la frequenza naturale smorzata utilizzando questo valore, il risultato è \({\omega_d}=0,995{\omega_n}\). Quindi, si consiglia di utilizzare \({\omega_d}{\spesso ca}{\omega_n}\).
Possiamo riassumere le proprietà dinamiche nella tabella seguente.
| Frequenza angolare (rad/s) | Frequenza naturale (Hz) | Periodo naturale (S) | |
|---|---|---|---|
| Frequenza angolare \({\omega_n}\) | \({\omega_n}\) | \(2{\pi}{f_n}\) | \(\frac{2{\pi}}{T_n}\) |
| Frequenza naturale \({f_n}\) | \(\frac{\omega_n}{2{\pi}}\) | \(f_n\) | \(\frac{1}{T_n}\) |
| Periodo naturale \({T_n}\) | \(\frac{2{\pi}}{\omega_n}\) | \(\frac{1}{f_n}\) | \(T_n\) |
tavolo 1. Relazione tra frequenza angolare, frequenza naturale, e periodo (Ciotola, 2017, . 60)
Più gradi di libertà
Quando esistono molte masse in una struttura, dobbiamo definire coordinate multiple per descrivere la posizione in qualsiasi momento per queste masse. Un esempio particolare ed evidente è mostrato nella figura seguente, costituito da un pendolo complesso in cui sono necessari angoli diversi per stabilire la posizione in ogni momento del movimento.
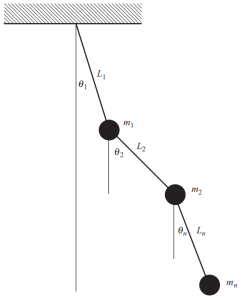
figura 4. Pendolo a masse multiple. (Ciotola, 2017, . 53)
In questa sezione, analizziamo le strutture’ risposta dinamica generale utilizzando l'estensione dell'analisi della frequenza delle proprietà per più gradi di libertà.
È fondamentale essere consapevoli del processo di modellazione quando si ha a che fare con una struttura reale. Le immagini seguenti descrivono i passaggi necessari per costruire un modello matematico pronto per applicare l'analisi in frequenza per descriverne la risposta dinamica.
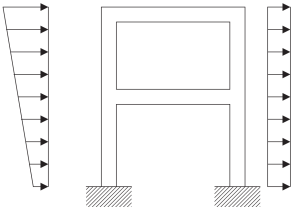
figura 5. Modello fisico di un telaio strutturale continuo. (Ciotola, 2017, . 23)
Il primo passaggio prevede il raggruppamento delle masse ad ogni intersezione di livello di travi e pilastri. Ogni nodo ha tre possibili movimenti, due spostamenti lineari, e una rotazione. Per essere coerenti nell'analisi, devono essere considerate le masse e le proprietà inerziali polari.
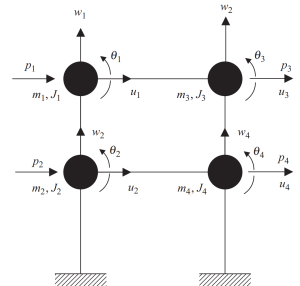
figura 6. Masse concentrate ai nodi con gradi di libertà di spostamento e rotazione. Sistema discreto. (Ciotola, 2017, . 23)
Il metodo della condensazione statica può aiutare a ridurre la complessità dell'analisi, trascurando l'inerzia rotazionale e traslazionale.
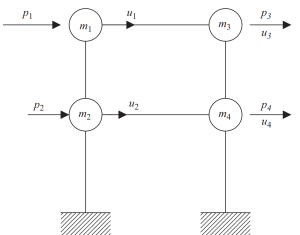
figura 7. Condensazione statica del grado di libertà al solo spostamento orizzontale. (Ciotola, 2017, . 23)
Nell'ultimo passaggio, possiamo raggruppare in soli due nodi il movimento orizzontale per questo esempio di frame.
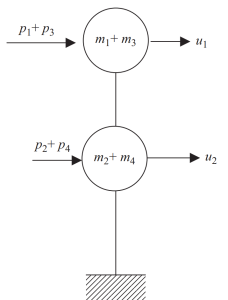
figura 8. Condensazione statica finale a due nodi e grado di libertà di spostamento orizzontale. (Ciotola, 2017, . 24)
Come abbiamo fatto nella sezione precedente con il sistema SDOF, svilupperemo la soluzione dell'equazione del moto per più gradi di libertà.
L'equazione del moto scrive in forma matriciale come
\([M]\{\punto{u}\} + [C]\{\punto{u}\}+[K]\{u\}={p(t)}\)
Dove:
- \([M]\) è la matrice di massa
- \([C]\) è la matrice di smorzamento di Coulumb
- \([K]\) è il matrice di rigidezza
Dobbiamo studiare la soluzione di vibrazione libera per ottenere i parametri di risposta. Non c'è smorzamento e forza applicata al sistema, solo le condizioni iniziali da valutare.
\([M]\{\punto{u}\} +[K]\{u\}={0}\)
In analogia al primo caso per un SDOF, possiamo testare una soluzione sinusoidale della forma.
\({u(t)}={\phi}{({un carico}{cos}{\omega}{t}+{b}{senza}{\omega}{t})}\)
\({\punto{u}{(t)}}={-{\omega}^ 2}{\phi}{({un carico}{cos}{\omega}{t}+{b}{senza}{\omega}{t})}\)
In cui il vettore \(\phi\) è un vettore di forma che non dipende dal tempo. I coefficienti “un carico” e “b” sono costanti ottenute valutando le condizioni iniziali.
Dopo aver sostituito entrambe le espressioni per la soluzione di prova nell'equazione del moto, otteniamo il problema lineare autovalore-autovettore:
\([K]{\phi}={{\omega}^ 2}[M]{\phi}\)
Dove:
- \({{\omega}^ 2}\) è l'insieme degli autovalori
- \({\phi}\) è l'insieme degli autovettori
La soluzione a questo classico problema per l'esempio del telaio nelle ultime figure mostra come vibreranno le masse. Ciò significa che ogni massa si muoverà in direzione orizzontale in base al valore degli autovettori.
Guarda la seguente immagine di questo comportamento.
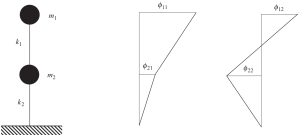
Figura n.9. Analisi di frequenza che mostra i risultati dei due autovettori. (Ciotola, 2017, Pagina 135)
SkyCiv Structural 3D
Esegui analisi di frequenza per le tue strutture con SkyCiv Structural 3D. Iscriviti oggi per iniziare!
Riferimenti:
- Eduardo Kausel, (2017). “Dinamica strutturale avanzata” 1prima edizione, Cambridge University Press


