Una guida alla determinazione statica, Indeterminazione, e instabilità

Una volta che la struttura è stata completamente modellata e i carichi sono stati applicati, è tempo di risolvere il sistema per trovare tutti i risultati che provengono dalla fase di analisi: reazioni, forze interne (forza di taglio, momento flettente, forza assiale, e torsione), spostamenti, e stress. A volte le cose non vanno come previsto e quando si tratta di risolverle, potresti ricevere un messaggio fastidioso che dice “Risoluzione non riuscita! Controlla la configurazione della tua struttura, poiché il modello è probabilmente instabile”, ed è probabile che tu non sappia esattamente cosa c'è che non va nel modello. Questo articolo spiega il concetto di stabilità strutturale insieme alla determinazione statica e all'indeterminazione che sono argomenti molto correlati, presenta inoltre alcuni suggerimenti per la risoluzione dei problemi di un modello instabile.

In generale, una struttura è considerata internamente stabile se mantiene la sua forma anche quando vengono rimossi i supporti. al contrario, una struttura è considerata internamente instabile se una volta staccata dai supporti, la struttura non riesce a mantenere la sua forma e può subire grandi spostamenti o addirittura crollare. Detto ciò, daremo uno sguardo più da vicino alla formula della determinabilità statica, sia per strutture internamente instabili che stabili. La formula di determinazione statica aiuta a classificare una struttura come esternamente instabile, staticamente determinato, o staticamente indeterminato.

Determinazione statica delle strutture internamente stabili

Una struttura internamente stabile può essere considerata staticamente determinata esternamente se tutte le sue reazioni di supporto possono essere risolte risolvendo le equazioni di equilibrio. Per strutture planari soggette a carichi nel piano, ci devono essere tre reazioni di supporto affinché la struttura sia in equilibrio. Inoltre, poiché sono disponibili solo tre equazioni di equilibrio, si possono trovare al massimo tre reazioni, quindi dovrebbero esserci esattamente tre reazioni a supporto della struttura piana. Alcuni esempi di strutture planari determinate staticamente esternamente sono mostrati nella figura seguente:

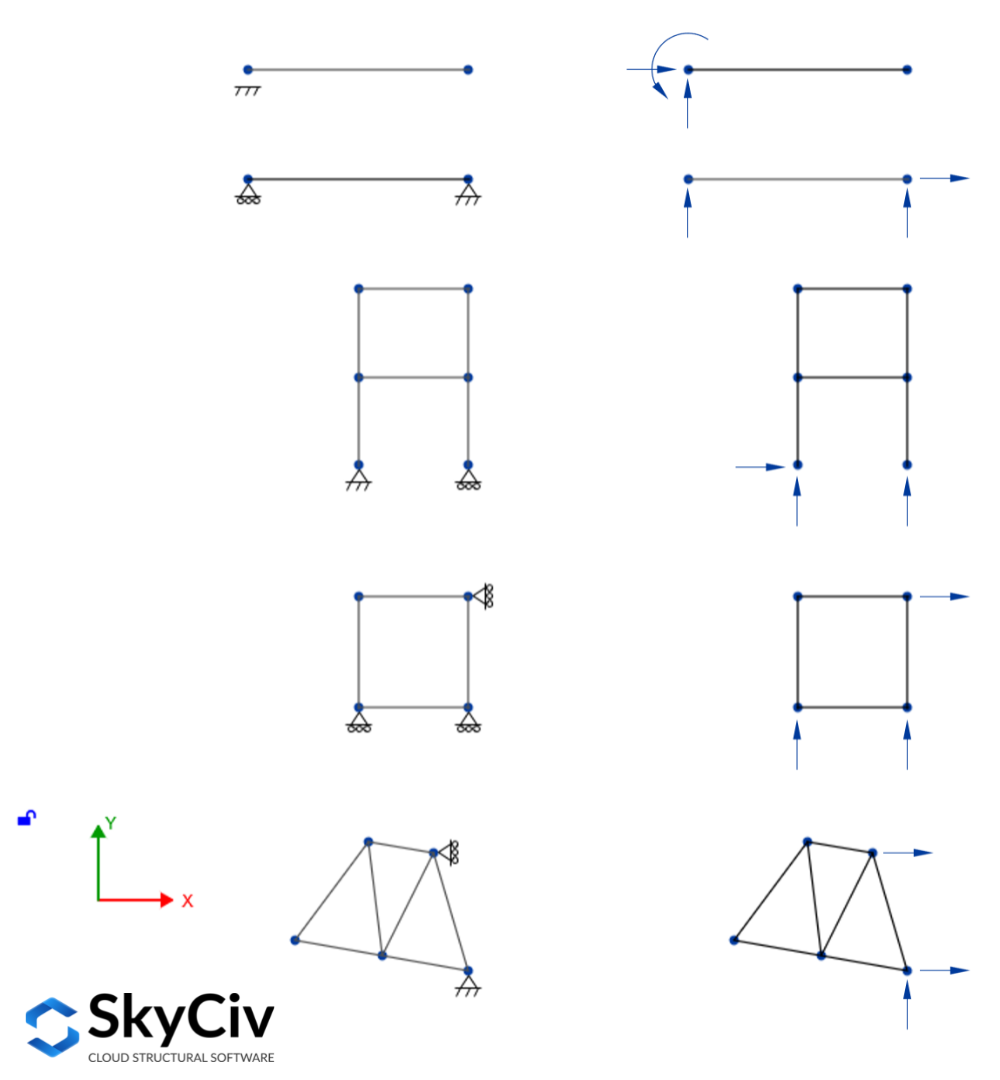
Quando più di tre reazioni supportano la struttura, è chiamata struttura esternamente staticamente indeterminata, poiché non è possibile risolvere tutte le reazioni utilizzando le tre equazioni di equilibrio. Tali reazioni sono chiamate ridondanza esterna e il numero di ridondanza esterna è noto come grado di indeterminazione esterna, scritto come un'equazione appare così:

\(io_e = r – 3\)

Dove \(r\) è il numero di reazioni che supportano la struttura.

Nei casi in cui la struttura è supportata da meno di tre reazioni di sostegno, questi non sono sufficienti per impedire alla struttura di spostarsi sul suo piano, poiché tale struttura non rimarrebbe in equilibrio sotto un sistema generale di carichi è detta staticamente instabile esternamente. In base al numero di reazioni \(r\), è possibile determinare la determinabilità statica, indeterminatezza, e instabilità di strutture internamente stabili utilizzando i criteri che seguono:

\( r \begin{considereremo il pannello solare a terra come un edificio a monopendenza aperta quando l'angolo di inclinazione è inferiore o uguale a 45° e come un segno solido per un angolo di inclinazione maggiore di 45°} < 3, \; \textrm{struttura esternamente staticamente instabile} \\ = 3, \; \textrm{struttura esternamente determinata staticamente} \\ > 3, \; \textrm{struttura esternamente staticamente indeterminata} \fine{considereremo il pannello solare a terra come un edificio a monopendenza aperta quando l'angolo di inclinazione è inferiore o uguale a 45° e come un segno solido per un angolo di inclinazione maggiore di 45°}\)

È importante menzionarlo una volta soddisfatte le ultime due condizioni, non è garantito che la struttura sarà stabile. Ciò significa che anche quando la struttura è supportata da più di tre reazioni, se supportata e non disposta correttamente la struttura potrebbe comunque essere instabile. Questa si chiama instabilità geometrica esterna ed è causata da due ragioni principali:

• Quando tutte le reazioni’ le linee di azione sono parallele perché alla struttura non sarà impedito di spostarsi nella direzione perpendicolare delle reazioni
• Quando tutte le reazioni’ le linee di azione sono concorrenti in un punto perché alla struttura sarà consentito ruotare attorno al punto di concorrenza

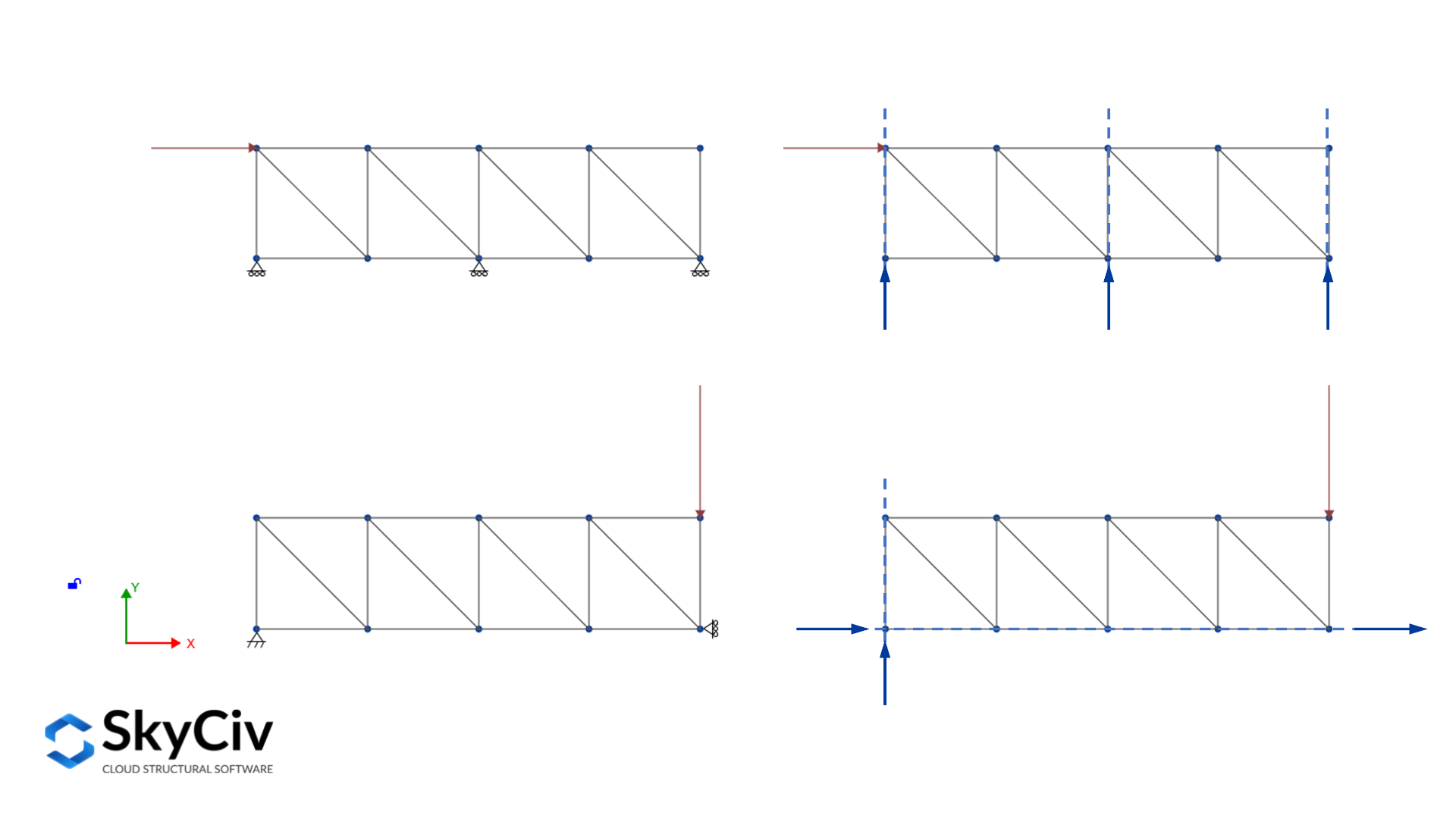
Determinazione statica delle strutture internamente instabili

Le strutture internamente instabili sono quelle che una volta staccate dai supporti non riescono a mantenere la forma originaria. Senza supporti, i membri della struttura subirebbero grandi spostamenti l’uno rispetto all’altro. Definire la determinabilità statica, indeterminatezza, e stabilità esterna di queste strutture, le equazioni cambiano a causa delle ulteriori equazioni di condizione che entrano in gioco tenendo conto delle connessioni speciali tra i membri. I collegamenti speciali sono quelli che non trasmettono momento, forza di taglio, o forza assiale.

Come esempio, considera la struttura nella figura qui sotto (sezione superiore), è chiaramente supportato da tre reazioni, ma queste non bastano a garantire l'equilibrio sotto le forze nel piano applicate grazie alla presenza della cerniera tra le membrature, ha bisogno di un quarto non parallelo, Reazione non contemporanea per garantire l’equilibrio (sezione inferiore).

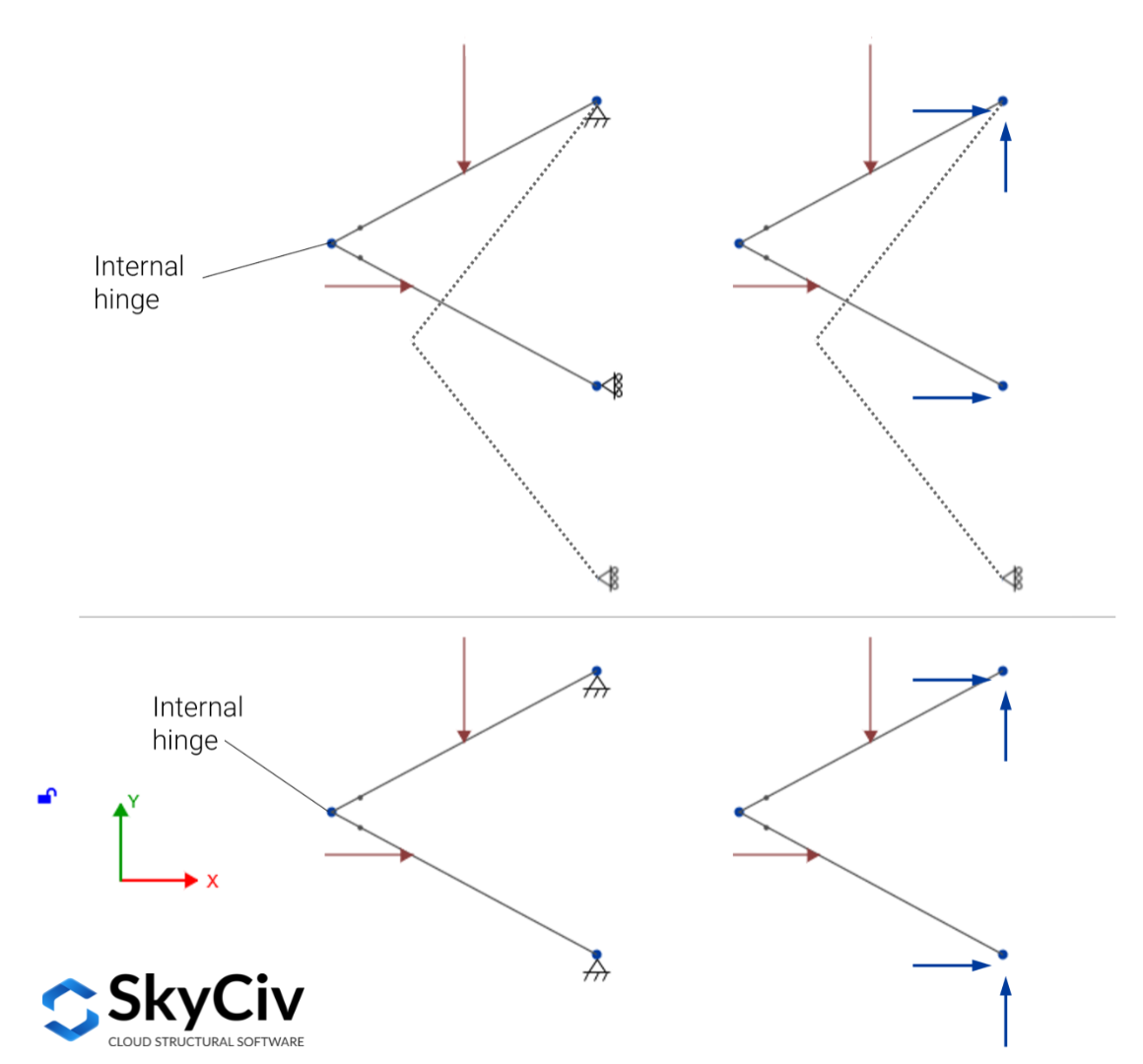
In generale, per strutture internamente instabili, in base al numero di reazioni \(r\) ed equazioni di condizione \(e_c\), è possibile determinare la determinabilità statica, indeterminatezza, e instabilità di strutture internamente stabili utilizzando i criteri che seguono:

\( r \begin{considereremo il pannello solare a terra come un edificio a monopendenza aperta quando l'angolo di inclinazione è inferiore o uguale a 45° e come un segno solido per un angolo di inclinazione maggiore di 45°} < 3 + e_c, \; \textrm{struttura esternamente staticamente instabile} \\ = 3 + e_c, \; \textrm{struttura esternamente determinata staticamente} \\ > 3 + e_c, \; \textrm{struttura esternamente staticamente indeterminata} \fine{considereremo il pannello solare a terra come un edificio a monopendenza aperta quando l'angolo di inclinazione è inferiore o uguale a 45° e come un segno solido per un angolo di inclinazione maggiore di 45°}\)

Per strutture indeterminate esternamente internamente instabili, il grado di indeterminatezza esterna può essere espresso come segue:

\(io_e = r – (3 + e_c)\)

Incartare

Per strutture planari che sono internamente stabili per essere esternamente stabili, il che significa che rimane in equilibrio sotto un sistema generale di carichi, deve valere quanto segue:

• La struttura è supportata da tre o più reazioni
• Tutte le reazioni non possono essere parallele né concorrenti

Per strutture planari che sono internamente instabili devono essere stabili esternamente, il che significa che rimane in equilibrio sotto un sistema generale di carichi, deve valere quanto segue:

• Il numero di reazioni che supportano la struttura è maggiore o uguale al numero di equazioni di condizione più tre
• Tutte le reazioni non possono essere parallele né concorrenti

Risoluzione dei problemi di una struttura instabile in S3D

Ci sono alcune cose che puoi provare quando il modello non risolve, e stai ottenendo il “Struttura instabile” messaggio di errore:

• Seleziona tutti i membri e assicurati che abbiano le relative fissazioni finali del membro “FFFFFF”, e provare a eseguire il modello. Se alcuni membri necessitano di un fissaggio finale diverso nel modello finale, iniziare a cambiarlo uno per uno e risolvere la struttura per vedere qual è l'esatto membro o insieme di membri che causa l'instabilità.
• Seleziona tutti i membri e cambia il loro tipo da normale a continuo, che collegherebbe correttamente i membri che non hanno un nodo nell'intersezione ma sono destinati ad essere collegati.
• Eliminare dall'analisi tutti i cavi, e provare a risolvere il modello. Per imparare come sopprimere i membri, fare riferimento a Questo articolo.

Riferimenti

Kassimali, Aslam. “3.4 Determinazione statica, Indeterminazione, e instabilità”. Analisi strutturale, Apprendimento Cengage, 2011.