MATERIALI ORTOTROPICI
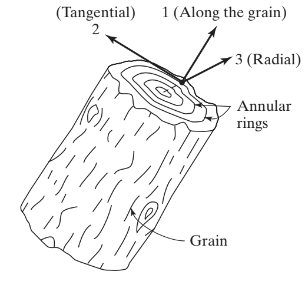
Prima di passare attraverso una spiegazione delle placche ortotrope, diamo un'occhiata ad alcuni esempi di materiali ortotropi. Materiali come cristalli di topazio e barite sono ortotropi (Chandrupatla, 2012). Un altro materiale ortotropo molto comune è il legno. figura 1 mostra gli assi principali in cui sono definite le proprietà meccaniche del legno.
figura 1. Il legno come materiale ortotropo (Chandrupatla & Belgundu ,2012, . 233)
minore 1 è definito lungo il grano o le fibre; asse 2 è tangenziale e asse 3 corre radialmente. La legge di Hooke generalizzata per questo esempio (e per qualsiasi altro materiale ortotropo) può essere scritto come
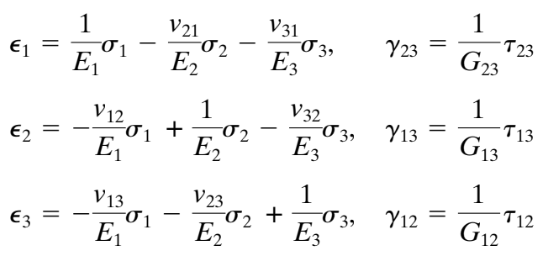
secondo il comando di ingegneria delle strutture navali 1. Legge di Hooke generalizzata (Chandrupatla & Belgundu,2012, . 233)
Dove:
- e1, e2, e3 sono i ceppi normali.
- c12, c13, c23 sono le deformazioni di taglio.
- E1, E2, e E3 sono il modulo di Young lungo l'asse principale.
- sol12, sol13, sol23 sono il modulo di taglio.
- n21, n31, n12, n32, n23 sono i rapporti di Poisson.
- Per indici combinati, il primo numero indica dove viene applicata la sollecitazione e il secondo dove si verifica la deformazione.
Pertanto, la principale differenza in un materiale ortotropo è che abbiamo diverse proprietà meccaniche lungo gli assi principali, questo è, “x”, “y”, “z”.
PLACCHE ORTOTROPE
Ci sono alcuni casi d'uso comuni per piatti in ingegneria strutturale, che possiamo riassumere come segue: piatto isotropo, composito o sandwich e irrigidito (W. Jiang et al, 1997).
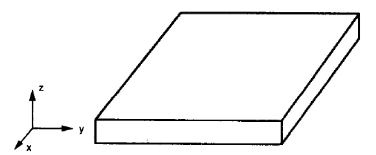
Le piastre piatte isotropiche sono piastre regolari (figura n.2), è solo necessario definire un valore uno per il rapporto di Poisson, Giovane, e modulo di taglio perché le proprietà meccaniche in qualsiasi direzione non cambiano.
Figura n.2. Le piastre piatte sono comunemente isotrope (W. Jiang et al, 1997, . 106)
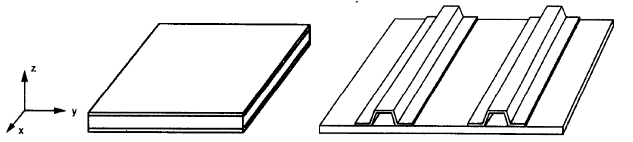
Per le ultime due opzioni, sandwich e piatti rigidi (figura n.3), dobbiamo definire diverse proprietà meccaniche nel loro asse principale. Questi diversi valori rendono le piastre ortotrope.
figura 3. Composito (sinistra) e piatti irrigiditi (giusto) (W. Jiang et al, 1997, . 106)
In una placca ortotropa, avremmo due assi con la stessa rigidità, figura n.3. Gli assi "x" e "y" giacciono su un piano, e "z" è perpendicolare ad esso.
Possiamo dirlo (W. Jiang et al, 1997):
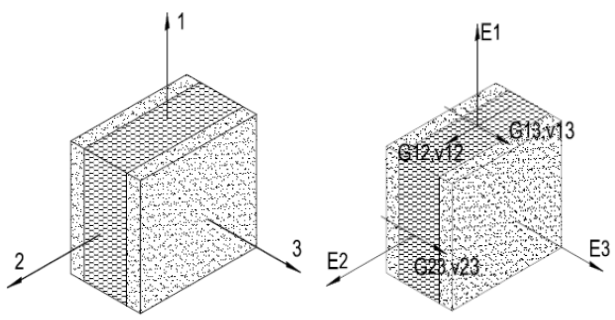
- Ex = Ey ≠ Ez ; (Ex, Ey )> Ez .
- nxz = nyz ≠ nxy ; (nxz, nyz) >nxy
- solxy = solxz = solyz
Le espressioni sopra indicate implicano che la rigidità nelle direzioni “x” e “y” sia maggiore di “z”. I rapporti di Poisson mostrano anche che c'è una maggiore deformazione nei piani relativi alla direzione "z" rispetto a un piano formato dagli assi "x" e "y".
ESEMPIO
Descrizione e configurazione
Per riassumere i concetti appresi nelle sezioni precedenti, svilupperemo un esempio in SkyCiv. Consiste nell'analisi di una parete sandwich/pannello lastra costituito da due strati di calcestruzzo proiettato separati da un'anima in polistirene. Abbiamo scelto il prossimo riferimento per le proprietà meccaniche da utilizzare nella modellazione: Torres Villavicencio et al. (2013).

figura 4. Pannello sandwich parete/lastra
Per catturare la differenza di analisi nelle lastre quando selezioniamo le opzioni avanzate (ortotropo), sviluppiamo un breve confronto del pannello sandwich sopra descritto e un'approssimazione delle loro proprietà meccaniche utilizzando un approccio isotropo. L'ultimo caso utilizza valori nelle proprietà meccaniche che non cambiano lungo i loro assi principali.
L'obiettivo di questo esempio è confrontare i risultati in termini di spostamento verticale. La configurazione del modello è mostrata in Figura 5.
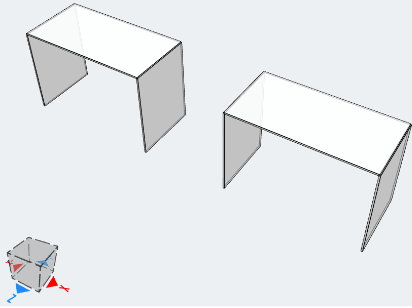 figura 5. Configurazione del modello. Ortotropo (sinistra), isotropo (giusto)
figura 5. Configurazione del modello. Ortotropo (sinistra), isotropo (giusto)
Proprietà meccaniche
Basato su diversi rapporti di test di laboratorio, le proprietà ortotropiche del pannello sono (Torres Villavicencio et al, 2013):
| Proprietà | Valore |
|---|---|
| E1 (MPa) | 5613 |
| E2 (MPa) | 5613 |
| E3 (MPa) | 2807 |
| sol12 (MPa) | 2245 |
| sol23 (MPa) | 1123 |
| sol13 (MPa) | 1123 |
| n12 | 0.2 |
| n23 | 0.25 |
| n13 | 0.25 |
Tabella n.1. Proprietà meccaniche ortotropiche del pannello sandwich
Figura n.6. Assi principali nell'elemento pannello (Torres Villavicencio et al, 2013).
L'approssimazione per il caso isotropo è indicata nella tabella seguente.
| Proprietà | Valore |
|---|---|
| E (MPa) | 5613 |
| sol (MPa) | 2245 |
| n | 0.20 |
Tabella n.2. Approssimazione delle proprietà meccaniche isotropiche del pannello sandwich
Modellazione in SkyCiv
Descriviamo ora in modo molto conciso i passaggi necessari per modellare l'esempio. (Per maggiori dettagli nella modellazione delle lastre, consulta questo link Modellazione di lastre SkyCiv). Non ho provato SkyCiv, seguire con Structural 3D, semplicemente iscriviti gratuitamente qui.
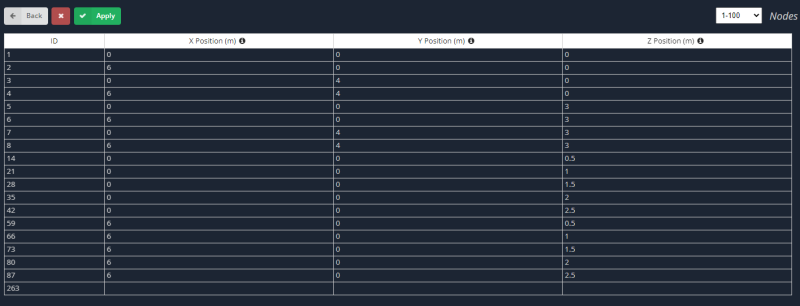
- nodi: Per creare entrambi i casi, definiamo prima i nodi corrispondenti alle piastre orizzontali e verticali.

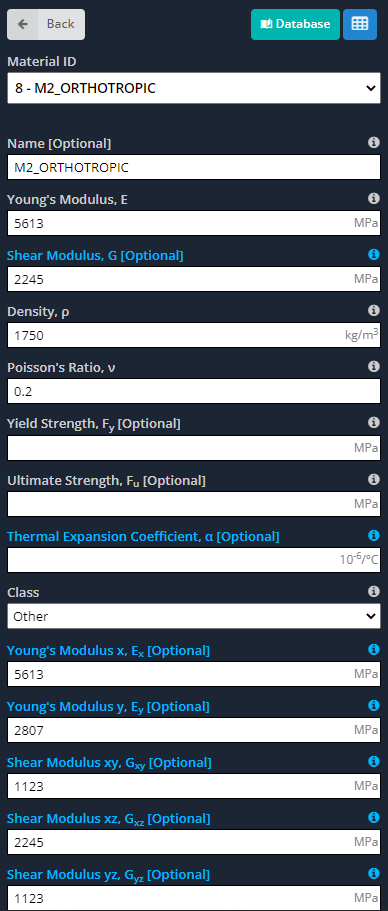
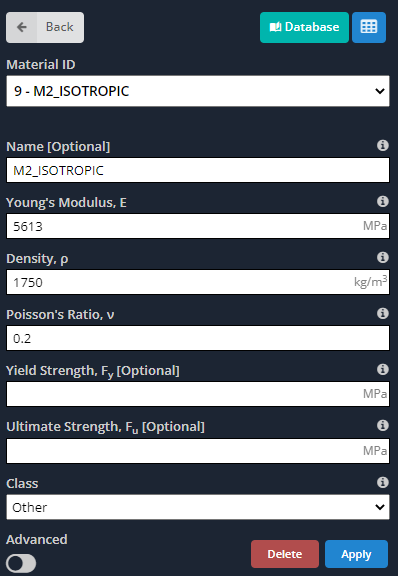
- materiale: Come abbiamo detto prima, i materiali ortotropi hanno proprietà diverse lungo i loro assi principali. Le immagini successive indicano gli input che dobbiamo definire per il modello.


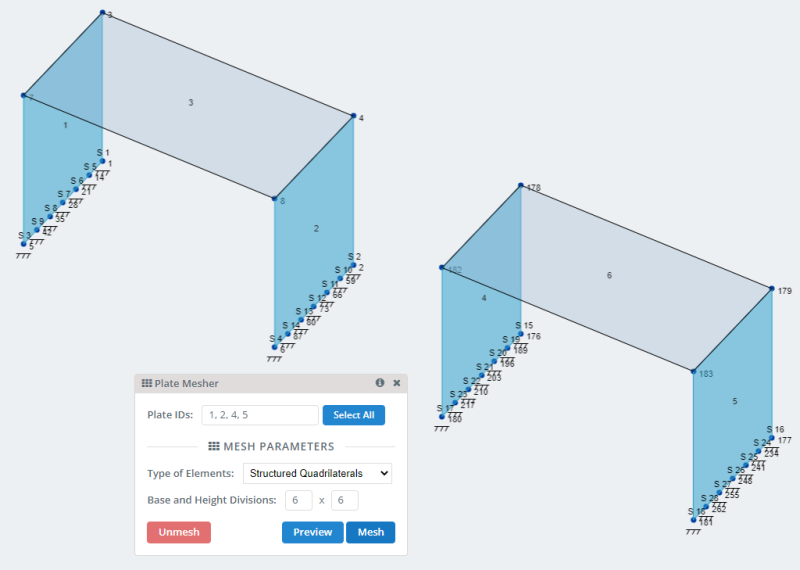
- Piatti: Attraverso i nodi modello creiamo le piastre rettangolari. Due per la modellazione della parete verticale e una per il pavimento o la soletta.

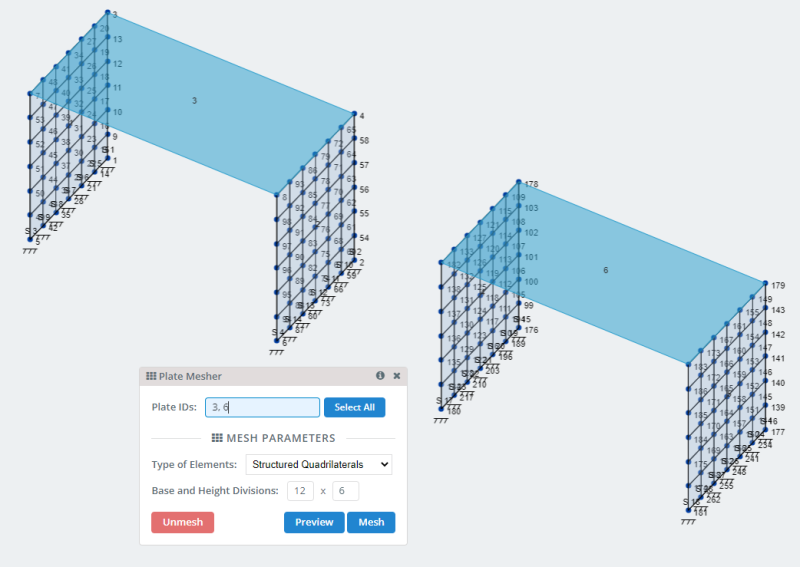
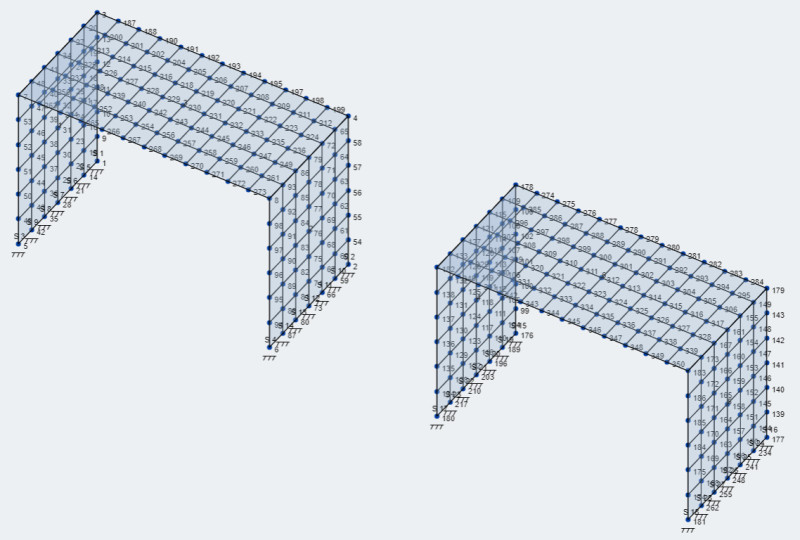
- Piastre a rete: SkyCiv ha molte opzioni per ingranare le piastre e può essere consultato in Ingranare il tuo piatto . Per il nostro modello utilizziamo l'opzione della mesh a quadrilateri strutturati.



- Definizione del caso di carico del proprio peso: Considereremo solo questo carico di peso proprio per catturare il comportamento strutturale generale della piastra.

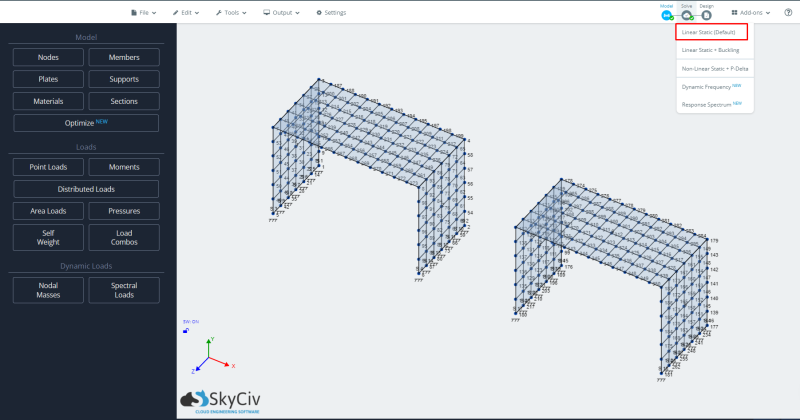
- Analisi in corso: Per eseguire il modello selezioneremo il caso di analisi statica lineare.

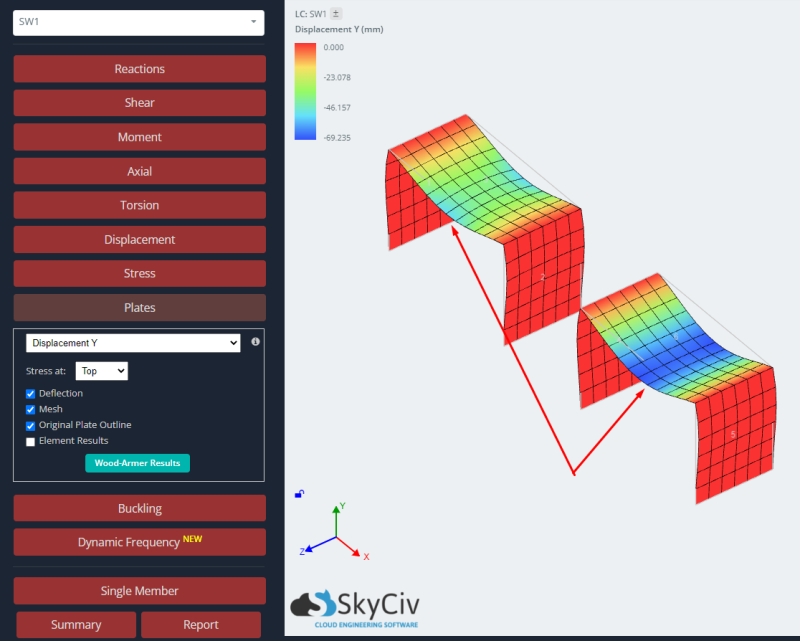
- risultati: Infine, a questo punto studiamo la risposta strutturale per entrambe le placche, il caso isotropo e ortotropo. Per ulteriori dettagli sulla lettura dei risultati per l'analisi della piastra, puoi guardare questo articolo Risultati dell'analisi delle piastre.

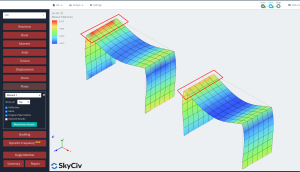
Per studiare la risposta di entrambi i casi, confrontiamo i risultati dello spostamento verticale e del momento flettente. La placca ortotropa mostra deviazioni minori e momenti flettenti maggiori rispetto al caso isotropo. Possiamo dire che l'uso di un approccio ortotropico ci darà un elemento più rigido e questo avrà un impatto sui risultati globali e locali in un'analisi lineare elastica.
Comincia gratuitamente
Guardare SkyCiv Structural 3D gratuitamente oggi per avere un assaggio del nostro software!
Riferimenti:
- Chandrupatla, Tirupati R & Belgundu, Ashok (2012). “Introduzione agli elementi finiti in ingegneria” 4esima edizione, Educazione Pearson.
- W. Jiang et al (1997). “Modellazione agli elementi finiti di placche ortotropiche irrigidite e non irrigidite”, Computer & Strutture Vol.63, n.1, pp. 105-117, Elsevier Science Ltd.
- Torres Villavicencio et al (2013). “opera monografica: Ausili alla progettazione per sistemi portanti EMMEDUE di pannelli in cemento armato con anima in E.P.S (Sistema in polistirene espanso)”. Università Nazionale di Ingegneria.
- Tutte le immagini del software prese da Software di analisi 3D strutturale SkyCiv