Una panoramica ed un esempio di calcolo dei carichi di neve ventata e come applicarli
I progetti del tetto di solito presentano moltitudini di elevazioni del tetto e raramente offrono una sola altezza del tetto. A causa di ciò, ci sono zone del tetto più alte e più basse l'una dell'altra e sono soggette a cumuli di neve. La quantità di carico di neve aggiuntivo, o supplemento, può e avrà un grande impatto sulla progettazione dei membri in queste aree.
La geometria del tetto e la direzione del vento sono i due driver che portano ai cumuli di neve. Le due direzioni del vento che provocano i cumuli di neve sono “sopravvento” e “di sottovento”. I cumuli di neve sopravento si verificano quando il vento soffia la neve da un tetto con elevazione inferiore verso il muro di un adiacente, tetto più alto. I cumuli di neve sottovento si verificano quando il vento spazza via la neve da un tetto più alto su un tetto inferiore adiacente. Guarda la figura 7-7 da ASCE 7-10 sotto per una rappresentazione succinta:

Supponiamo che il nostro progetto sia a Madison, Wisconsin e abbiamo già calcolato il nostro equilibrato, carico di neve sul tetto Qui. Dal nostro esempio, il nostro carico a terra e il carico di neve sul tetto piatto sono risultati 30 PSF e 21 PSF, rispettivamente. Le disposizioni su come calcolare il supplemento di neve ventata per le strutture possono essere trovate nella Sezione 7.8 dell'ASCE 7-10.
Il tetto della nostra struttura di esempio ha due altezze del tetto variabili e quindi dobbiamo calcolare il supplemento per il cumulo di neve e applicarlo ai nostri membri. Nel nostro caso, i nostri raggi sono distanziati a 10 piedi.
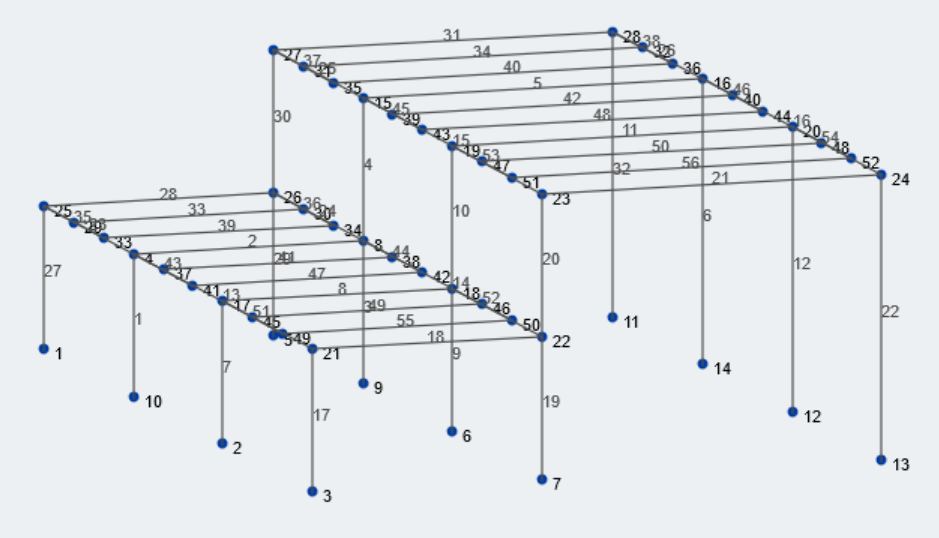
figura 1: Vista isometrica della nostra struttura di esempio
Raccogliamo prima le informazioni geometriche rilevanti sulla nostra struttura. La dimensione della baia inferiore e della baia superiore è 25 piedi e 37 piedi, rispettivamente. Le elevazioni del tetto inferiore e superiore sono 15 piedi e 30 piedi dal grado, rispettivamente. La maggior parte dei valori geometrici può essere associata a variabili. Diamo uno sguardo a tutte le variabili pertinenti per questo calcolo.
\({p}_{g}\) = carico di neve al suolo
\({l}_{u}\) = lunghezza del tetto superiore
\({l}_{l}\) = lunghezza del tetto inferiore
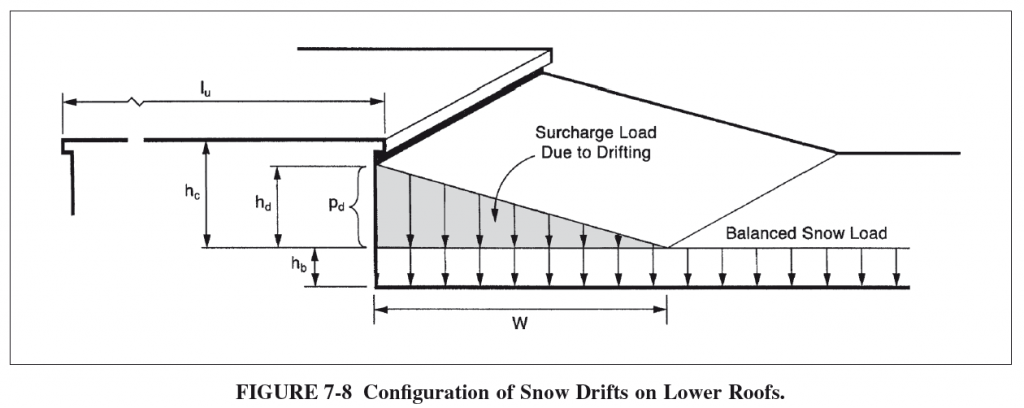
\({h}_{d}\) = altezza del cumulo di neve
\({w}\) = larghezza del cumulo di neve
\({h}_{b}\) = altezza del carico di neve equilibrato
\({h}_{c}\) = altezza libera dalla parte superiore del carico di neve bilanciato al punto più vicino del tetto adiacente
\({h}_{r}\) = differenza di altezza tra i tetti
\({p}_{S}\) = carico neve di progetto dal capitolo 7
\({c}\) = densità della neve
\({p}_{d}\) = carico di neve ventata
Dai un'occhiata alla figura 7-8 da ASCE 7-10 per una rappresentazione di molti di questi termini e di ciò che rappresentano visivamente:
Trovare il carico di sovraccarico deriva dalla neve
Ora che abbiamo identificato quali sono le variabili, le configurazioni di carico neve, e i vincoli geometrici della nostra struttura, calcoliamo la deriva della neve.
Primo, scoprire se è necessario il caricamento di cumuli di neve, per ASCE 7.7-1:
Se \({h}_{c}/{h}_{b} < 0.2\), quindi l'applicazione del cumulo di neve non è necessaria.
\({h}_{b} = {p}_{S}/{c}\), dove:
\({c} = 0.13{p}_{g} + 14 ≤ 30 pcf\)
\({c} = 0.13*(30) + 14 = 17.9 pcf ≤ 30 pcf \)
\({h}_{b} = {21 PSF}/{17.9 pcf } = 1.17 piedi)
\({h}_{c} = {h}_{r}-{h}_{b}\)
\({h}_{c} = 15 ft – 1.17 ft = 13.8 piedi)
\({h}_{c}/{h}_{b} = 13.8 piedi / 1,17 piedi = 11.8 > 0.2\) e quindi, è necessario il caricamento di cumuli di neve.
Secondo, trova la massima altezza di deriva tra le direzioni sopravento e sottovento:
L'altezza della deriva per entrambe le direzioni del vento può essere trovata utilizzando l'equazione che si trova in Figura 7-9 dell'ASCE 7-10, mostrato sotto:
\({h}_{d} = 3/4*(0.43({l}_{l})^{1/3}({p_g}+10)^{1/4}-1.5)\) per deriva al vento
\({h}_{d} = 0.43({l}_{u})^{1/3}({p_g}+10)^{1/4}-1.5\) per deriva sottovento
Altezza di deriva al vento:
\({h}_{d} = 3/4 *(0.43(25 ft)^{1/3}(30 psf + 10)^{1/4}-1.5)\)
\({h}_{d} = 1.25 piedi)
Altezza della deriva sottovento:
\({h}_{d} = 0.43(37 ft)^{1/3}(30 psf + 10)^{1/4}-1.5\)
\({h}_{d} = 2.1 piedi)
L'altezza massima di deriva tra l'altezza di deriva sopravento e sottovento sarà utilizzata per la progettazione, perciò:
\({h}_{d} = 2.1 piedi)
Successivamente, trova l'ampiezza del supplemento per il cumulo di neve:
La larghezza del carico del cumulo di neve, \({w}\), dipende da \({h}_{c}\) e \({h}_{d}\)
Per sezione 7.7.1,
Se \({h}_{d} ≤ {h}_{c}\), poi \({w} = 4{h}_{d}\)
Se \({h}_{d} > {h}_{c}\), poi \({w} = 4{h}_{d}^ 2 /{h}_{c}) e successivamente \({h}_{d} = {h}_{c}\)
Nel nostro caso, \({h}_{c} = 13.8 piedi) e \({h}_{d} = 2.1 piedi), e quindi:
\({h}_{d} ≤ {h}_{c}\), e
\({w} = 4*(2.1 ft)\)
\({w} = 8.4 piedi)
Nota, per ASCE 7-10 il la larghezza del cumulo di neve non deve mai superare \(8{h}_{c}\)
Scorso, calcolare il carico di sovraccarico della deriva da neve:
Per trovare il carico massimo del supplemento, moltiplicare l'altezza della deriva per la densità della neve:
\({p}_{d} = {h}_{d}{c}\)
Nel nostro caso,
\({p}_{d} = (2.1 ft)*(17.9 pcf )\)
\({p}_{d} = 37.6 psf)
Il carico massimo del cumulo di neve viene quindi sovrapposto al carico di neve bilanciato:
\({p}_{max} = {p}_{d}+{p}_{S}\)
\({p}_{max} = 58.6 psf)
Applicazione dei carichi di sovraccarico della deriva della neve
Vediamo il frame centrale della nostra struttura. L'area distribuita per le travi in questo piano è 10 ft a causa della costante 10 distanza tra i piedi. figura 2 mostrato sotto mostra il carico di neve equilibrato di 21 psf applicato al tetto della nostra struttura. Nota, tutti i valori non sono presi in considerazione, carichi di servizio.
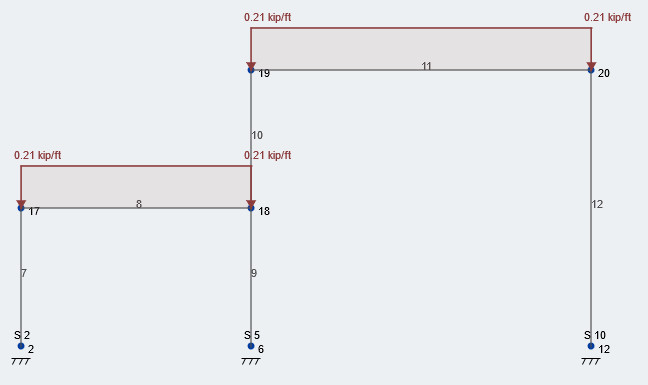
figura 2: Condizione di carico tipica del carico di neve equilibrato
Adesso, prendiamo il sovraccarico del cumulo di neve e lo sovrapponiamo alla nostra struttura. figura 3 rappresenta il carico di deriva aggiuntivo nella posizione corretta. Come potete vedere, il nostro carico di neve totale è 58.6 PSF – arrotondato a 59 PSF – situato alla faccia del muro e poi decresce linearmente sopra il 8.4 larghezza di deriva in piedi di nuovo al carico di neve bilanciato costante. Questa condizione di carico segue l'intera lunghezza del muro, nel nostro corso, la lunghezza della struttura.
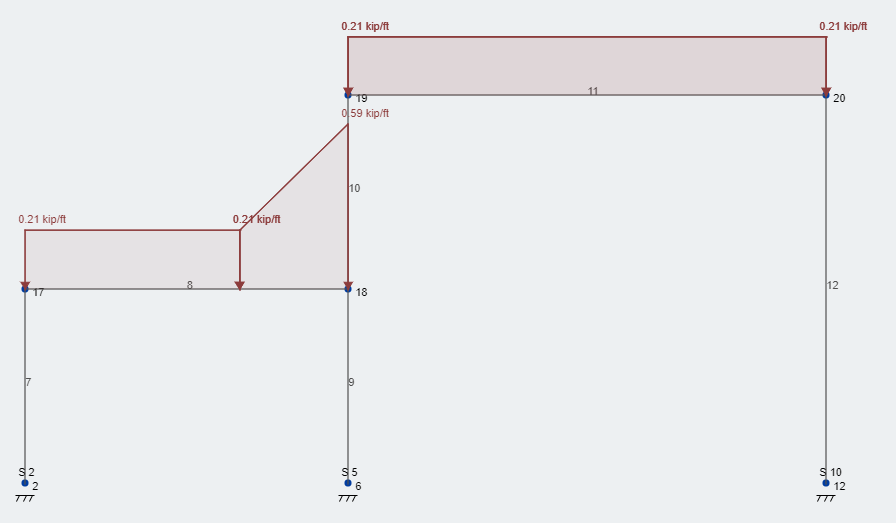
figura 3: Condizioni di carico tipiche del livello di servizio dei carichi di progetto della neve
A questo punto i carichi di neve sono pronti per l'analisi in congiuntura con altri casi di carico e combinazioni di carico basati su ASCE 7-10 e altri codici di costruzione pertinenti. Assicurati di leggere il capitolo 7 dell'ASCE 7-10 per maggiori informazioni sulle disposizioni successive per il carico di neve parziale e il carico di neve sbilanciato, poiché quelle condizioni non sono state valutate qui.
Riferimenti:
- Carichi minimi di progettazione per edifici e altre strutture. (2013). ASCE/SEI 7-10. American Society of Civil Engineers.


