Calcola le frequenze naturali della tua struttura in Structural 3D
Analisi di frequenza dinamica, o analisi modale, è necessario per determinare le frequenze naturali (o frequenze di risonanza) di una struttura per prevederne la massima risposta. Quando un carico di vibrazione applicato alla struttura corrisponde alla frequenza naturale, può essere pericoloso e portare alla distruzione del sistema.
Ingresso
Gli utenti possono aggiungere facilmente masse nodali, semplicemente convertendo i loro carichi statici esistenti in masse nodali. SkyCiv Structural 3D calcolerà automaticamente le masse nodali (in base ai gruppi di carico) e applicarli alla struttura, così il tuo modello può essere analizzato per effetti di frequenza dinamica. Iniziare, clic Masse nodali dal menu a sinistra. Gli utenti possono convertire le masse nodali dai carichi esistenti. Ecco un esempio di quando un utente fa clic Converti carichi sotto il Masse nodali ingresso:
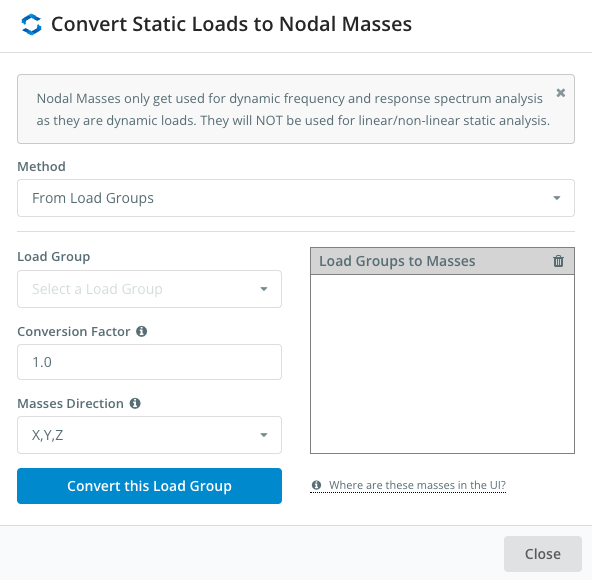
Ciò consente agli utenti di aggiungere gruppi di carico e convertirli in masse modali, dando all'utente il pieno controllo di quali carichi sono inclusi, con controlli per direzioni e fattori di massa.
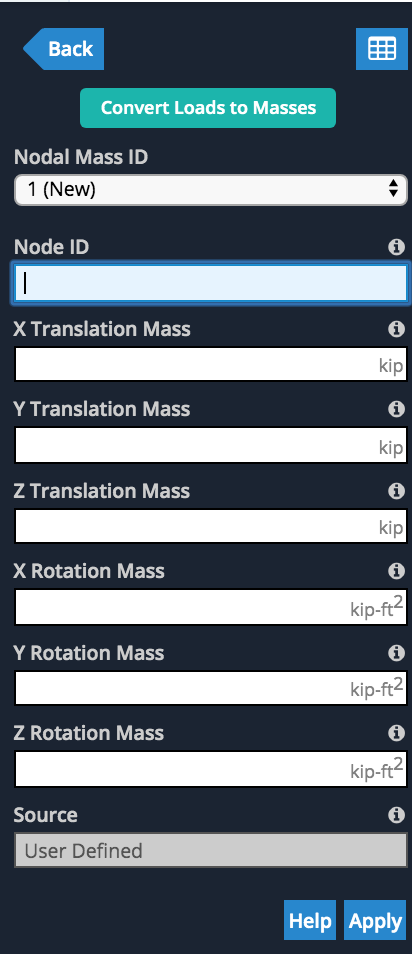
Gli utenti possono anche specificare le proprie masse nodali in qualsiasi nodo inserendo la X,E,Z valori di massa traslazionale e rotazionale:
Analisi di frequenza dinamica
L'analisi SkyCiv Dynamic Frequency calcola le frequenze proprie più basse della struttura, risolvendo l'equazione agli autovalori qui sotto. In un'analisi statica, stiamo assumendo che il sistema non dipenda dal tempo. Nell'analisi dinamica, c'è una dipendenza dal tempo.
Durante l'analisi della frequenza dinamica stiamo risolvendo le forme modali e le frequenze sotto vibrazione. Nello specifico risolviamo la frequenza vibrazionale (cicli al secondo) e periodo (il tempo impiegato per completare un ciclo) per ogni forma modale della struttura.
La seguente formula rappresenta i calcoli eseguiti da Structural 3D durante un'analisi di frequenza:
[M][U¨]+[K][U]=[0]
[M] = Matrice massa struttura,
[K] = Matrice di rigidezza della struttura,
[U] = spostamento,
[U¨] è la doppia derivata dello spostamento rispetto al tempo (vale a dire. accelerazione).
Qui, l'equazione non è risolta, ma piuttosto si riduce a un problema generale agli autovalori. Dove λ = autovalori
[M][U]λ+[K][U]=[0]
Gli autovalori risultanti sono le frequenze della struttura mentre gli autovettori sono le forme modali. Una frequenza o modalità più bassa significa meno cicli al secondo e quindi un'oscillazione più lenta.
Visualizzazione dei risultati
Una volta completata l'analisi della frequenza dinamica, gli utenti possono rivedere i risultati di più forme modali. Basta selezionare la forma della modalità, e la struttura si animerà per mostrare la forma della modalità. Gli utenti possono anche rivedere i valori di frequenza e periodo per tutte le modalità della struttura. Ecco un esempio dell'animazione e dei risultati:
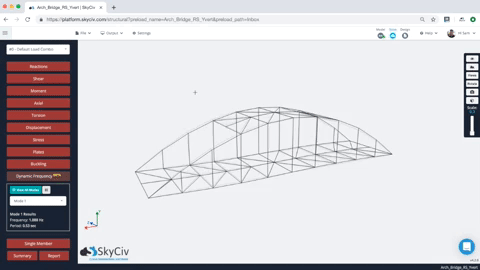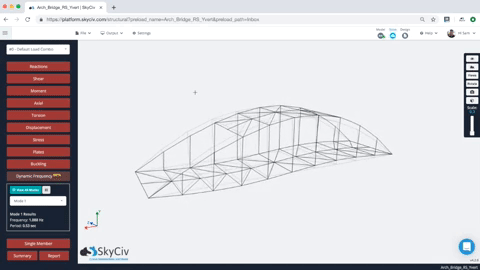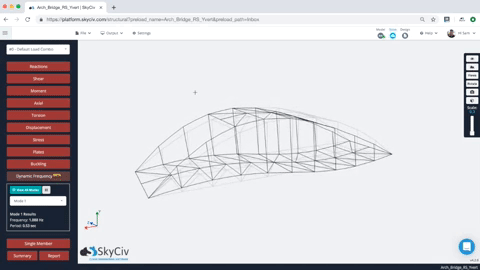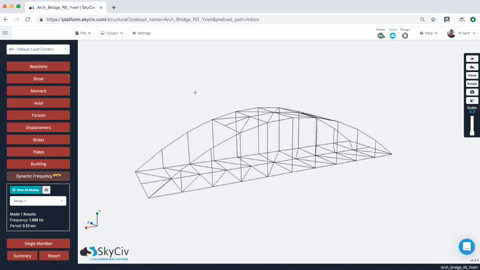
Agli utenti viene inoltre fornito un insieme tabulato di risultati per ciascuna modalità, compresa la frequenza naturale e il periodo. Così per esempio, nel modello sopra abbiamo la frequenza e il periodo di ciascun risultato (nota per semplicità, solo il primo 10 sono state generate le modalità – questo può essere controllato sotto impostazioni):
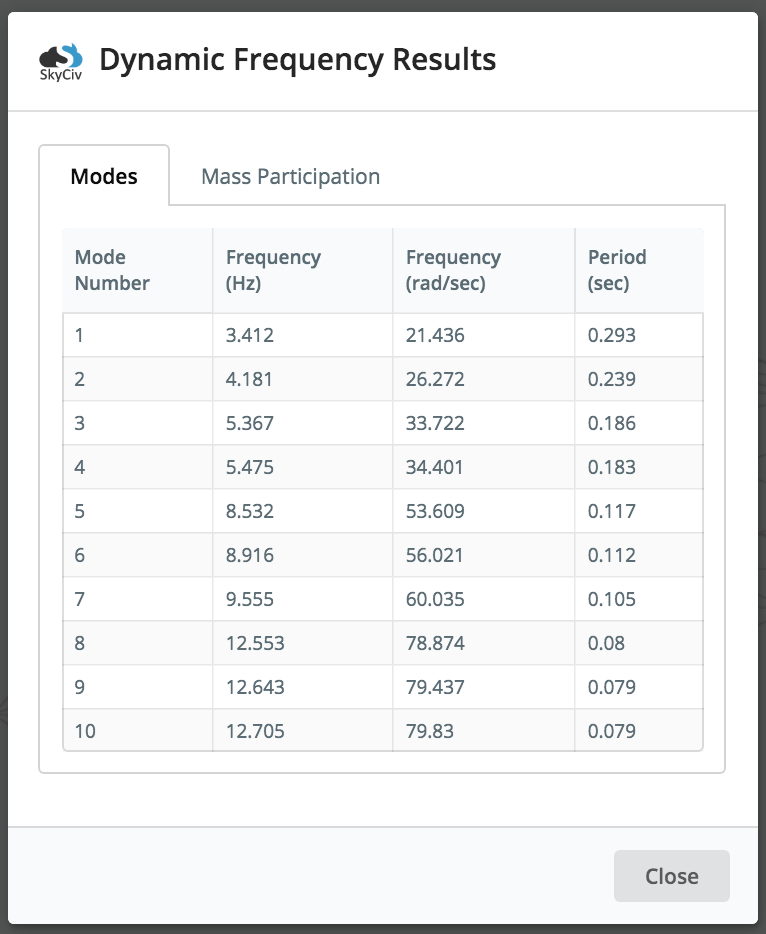
Inoltre, i risultati della partecipazione di massa modale di una struttura, e le sue modalità possono essere riviste facendo clic su Partecipazione di massa tab. Il fattore di partecipazione di massa rappresenta la quantità di massa associata alla specifica frequenza o modalità di vibrazione. Essenzialmente consente all'utente di vedere quanta parte della massa della struttura è eccitata con la modalità data. Dando così spunti sulla risposta della struttura: maggiore è il fattore di partecipazione di massa, maggiore è il suo significato per la risposta complessiva.
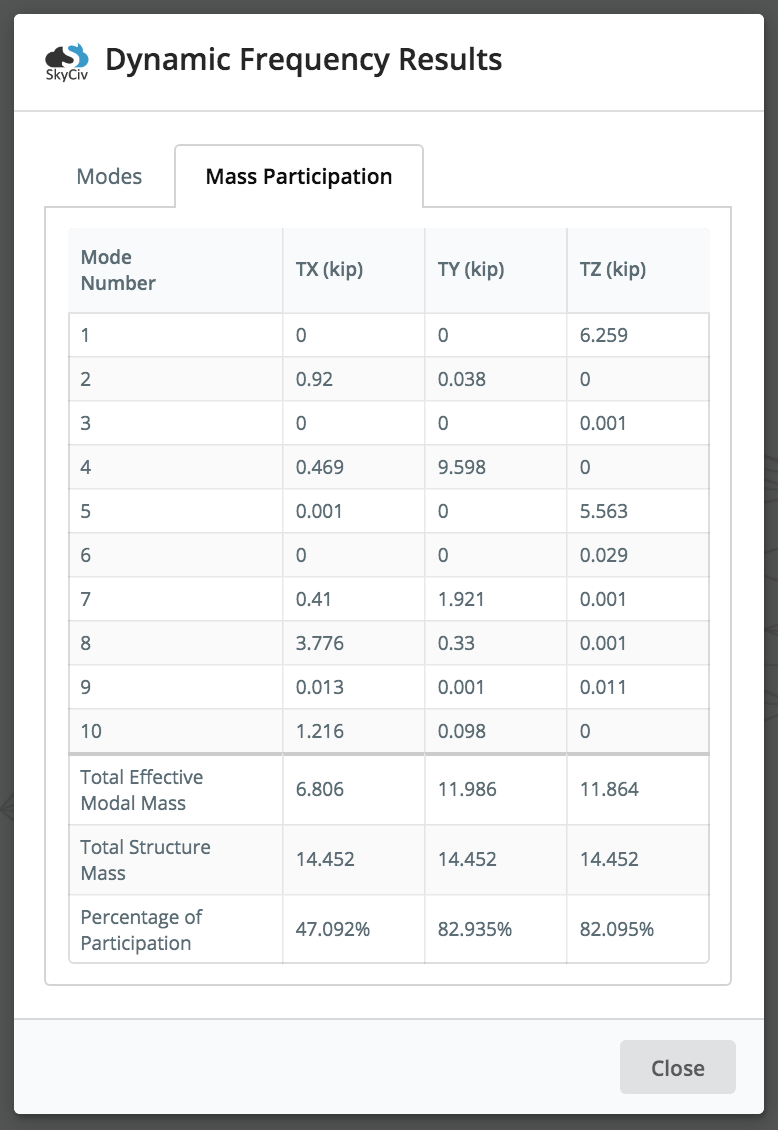
Nell'animazione di esempio sopra (la struttura del ponte), puoi vedere che il ponte si muove/vibra SOLO lungo le direzioni x e y per questa modalità (Modalità 2), quindi da quello, si ottiene 0 fattori di partecipazione all'interno della direzione z (lateralmente). Quando si ha a che fare con fattori di partecipazione di massa relativamente piccoli, l'utente dovrebbe sempre esercitare un giudizio tecnico e analizzare gli effetti di queste modalità di vibrazione. La maggior parte dei regolamenti edilizi richiede almeno 90% partecipazione cumulativa di massa per l'analisi.
