Una guida dettagliata ai calcoli per la progettazione di un plinto isolato (ACI 318-14)
La fondazione è un sistema costruttivo essenziale che trasferisce le forze della colonna e del muro al terreno di supporto. L'ingegnere potrebbe optare per un sistema di fondazione superficiale o profondo in base alle caratteristiche del terreno e ai carichi dell'edificio.
Modulo di progettazione della Fondazione SkyCiv comprende l'analisi e la progettazione del plinto isolato conforme alla normativa americana ACI318-14.
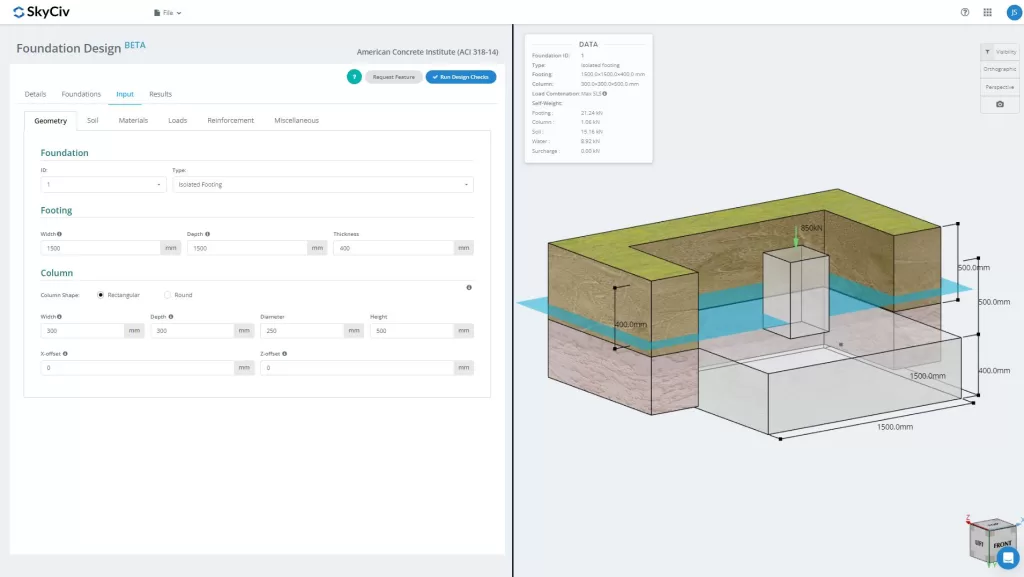
Vuoi provare il software Foundation Design di SkyCiv? Il nostro strumento consente agli utenti di eseguire calcoli di progettazione della fondazione senza scaricare o installare!
Una guida passo passo per progettare una fondazione isolata
Requisiti di dimensione
Per determinare le dimensioni di un plinto isolato, servizio o carichi non fattorizzati, come morto (D), Vivere (L), Vento (W), Sismico (E), ecc. verrà applicato utilizzando Combinazioni di carico, come definito da ACI 318-14. Qualunque combinazione di carico governa sarà considerata il carico di progetto, e viene confrontata con la pressione del suolo ammissibile come mostrato nell'equazione 1, come consigliato in Sezione 13.2.6 of ACI 318-14.
\(\testo{q}_{\testo{un carico}} = frac{\testo{P}_{\testo{n}}}{\testo{A}} \freccia destra \) Equazione 1
qun carico = Pressione del suolo ammissibile
Pn = Carico di progetto non fattorizzato
A = Area della fondazione
Le dimensioni della fondazione possono essere inizialmente stimate risolvendo l'area della fondazione (A) utilizzando l'equazione 1.
\(\testo{A} = frac{\testo{P}_{\testo{n}}}{\testo{q}_{\testo{un carico}}} \freccia destra \) Equazione 1a
Taglio unidirezionale
Lo stato limite di taglio unidirezionale, noto anche come taglio della trave, riconosce che la fondazione può cedere a taglio simile a una trave larga lungo un piano di taglio critico situato a distanza “d” dalla faccia della colonna (figura 1),
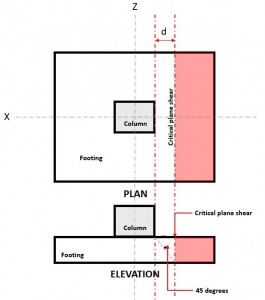
figura 1. Taglio del piano critico di taglio unidirezionale
La Senso unico cesoia Richiesta o V u è calcolato presupponendo che la fondazione sia a sbalzo lontano dalla colonna dove l'area rossa è indicata in Figura 1, seguente Sezione 8.5.3.1.1.
La Capacità di taglio unidirezionale o ϕVc è definita come la resistenza al taglio ultima e calcolata utilizzando l'equazione 2 per Sezione 22.5.5.1.
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 2 \sqrt{\testo{f ’}_{\testo{c}}} \volte testo{b}_{\testo{w}} \volte testo{d} \freccia destra \) Equazione 2 ( Sezione 22.5.5.1, Imperiale)
o
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 0.17 \sqrt{\testo{f ’}_{\testo{c}}} \volte testo{b}_{\testo{w}} \volte testo{d} \freccia destra \) Equazione 2 (Sezione 22.5.5.1, metrico)
ϕcesoia = Fattore di progetto a taglio
f’c = Resistenza del calcestruzzo specificata, (psi, MPa)
bw = Larghezza del plinto, (pollici, mm)
d = Distanza dalla fibra di compressione estrema al baricentro del rinforzo teso longitudinale, (pollici, mm)
La richiesta di taglio e la capacità di taglio devono soddisfare la seguente equazione per soddisfare i requisiti di progettazione di ACI 318-14:
\(\testo{V }_{\testo{u}} \leq phi text{V }_{\testo{c}} \freccia destra \) Equazione 3 (ACI Eq. 7.5.1.1(b))
Modulo di progettazione della Fondazione SkyCiv, in accordo con l'equazione 3, calcola il rapporto di utilità di taglio unidirezionale (Equazione 4) considerando la domanda di taglio rispetto alla capacità di taglio.
\( \testo{Rapporto di utilità} = frac{\testo{Shear Demand}}{\testo{Capacità di taglio}} \freccia destra \) Equazione 4
Taglio a due vie
Lo stato limite di taglio bidirezionale, noto anche come taglio da punzonatura, estende la sua sezione critica a distanza “d / 2” dalla faccia della colonna e attorno al perimetro della colonna (figura 2).
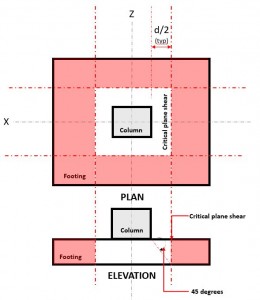
figura 2. Piano di taglio critico del taglio a due vie
La Due stradeascolta la domanda o V u si verifica sul piano di taglio critico, situato ad una distanza di “d / 2” dove il (rosso) area tratteggiata, indicato in figura 2, seguente Sezione 22.6.4.
La Capacità di taglio o ϕVc è governato dal valore più piccolo calcolato utilizzando le equazioni 5, 6, e 7 per Sezione 22.6.5.2
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 4 \times lambda times sqrt{\testo{f ’}_{\testo{c}}} \freccia destra \) Equazione 5 (Sezione 22.6.5.2(un carico) Imperiale)
\(\phi text{V }_{\testo{c}} = sinistra ( 2 + \frac{4}{\beta } \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 6 (Sezione 22.6.5.2(b) Imperiale)
\(\phi text{V }_{\testo{c}} = sinistra ( 2 + \frac{\alfa _{S} \volte d }{b{Il}} \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 7 (Sezione 22.6.5.2(c) Imperiale)
o
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 0.33 \times lambda times sqrt{\testo{f ’}_{\testo{c}}} \freccia destra \) Equazione 5 (Sezione 22.6.5.2(un carico) metrico)
\(\phi text{V }_{\testo{c}} = 0.17 \volte sinistra ( 1 + \frac{2}{\beta } \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 6 (Sezione 22.6.5.2(b) metrico)
\(\phi text{V }_{\testo{c}} = 0.0083 \volte sinistra ( 2 + \frac{\alfa _{S} \volte d }{b{Il}} \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 7 (Sezione 22.6.5.2(c) metrico)
Nota: β è il rapporto tra il lato lungo e il lato corto della colonna, carico concentrato, o area di reazione e αS è dato da 22.6.5.3
λ = Fattore di modifica per riflettere le ridotte proprietà meccaniche del calcestruzzo leggero rispetto al calcestruzzo normale con la stessa resistenza a compressione
f’c = Resistenza alla compressione specificata del calcestruzzo (psi, MPa)
d = Distanza dalla fibra di compressione estrema al baricentro del rinforzo teso longitudinale, (pollici, mm)
La richiesta di taglio e la capacità di taglio devono soddisfare la seguente equazione per soddisfare i requisiti di progettazione di ACI 318-14:
\(\testo{V }_{\testo{u}} \leq phi text{V }_{\testo{c}} \freccia destra \) Equazione 8 (Sezione 7.5.1.1(b))
Modulo di progettazione della Fondazione SkyCiv, in accordo con l'equazione 8, calcola il rapporto di utilità del taglio bidirezionale (Equazione 9) considerando la domanda di taglio rispetto alla capacità di taglio.
\( \testo{Rapporto di utilità} = frac{\testo{Shear Demand}}{\testo{Capacità di taglio}} \freccia destra \) Equazione 9
Flessione
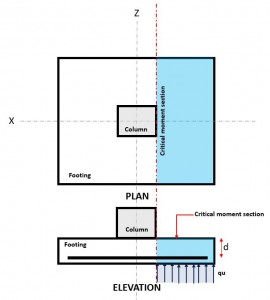
figura 3. Sezione flessione critica
La Flessionale lo stato limite si verifica in la sezione flessione critica, situato sulla faccia della colonna in cima al basamento (figura 3).
La Domanda flessionale o Mu si trova nella sezione di flessione critica (area blu del tratteggio) indicato in figura 3, e viene calcolato utilizzando l'equazione 10.
\( \testo{M}_{u} = testo{q}_{u} \volte sinistra ( \frac{l_{x}}{2} – \frac{c_{x}}{2} \giusto ) \volte l_{z} \volte sinistra ( \frac{\frac{l_{x}}{2} – \frac{c_{x}}{2} }{2} \giusto ) \freccia destra \) Equazione 10
qu = pressione del suolo fattorizzata, (ksf, kPa)
lx = dimensione della fondazione lungo l'asse x (pollici, mm)
lz = dimensione della fondazione lungo l'asse z (pollici, mm)
cx = dimensione della colonna lungo l'asse x (pollici, mm)
La Capacità flessionale o ϕMn viene calcolato utilizzando l'equazione 11.
\( \phi text{M}_{n} = phi_{\testo{flessione}} \volte A_{S} \volte f_{y} \volte sinistra( d – \frac{un carico}{2} \giusto) \freccia destra \) Equazione 11
ϕ = fattore di progettazione flessionale
lx = dimensione della fondazione parallela all'asse x (pollici , mm)
lz = dimensione della fondazione parallela all'asse z (pollici , mm)
d = distanza dalla fibra a compressione estrema al baricentro dell'armatura a trazione longitudinale (pollici , mm)
AS = area di rinforzo (pollici2 , mm2)
a = profondità del blocco di sollecitazione rettangolare equivalente (pollici , mm)
fy = forza di rinforzo, (KSI, MPa)
Moment Demand e Moment Capacity devono soddisfare la seguente equazione per soddisfare i requisiti di progettazione di ACI 318-14:
\(\testo{M}_{\testo{u}} \leq phi text{M}_{\testo{n}} \freccia destra \) Equazione 12 (Sezione 7.5.1.1(b))
Modulo di progettazione della Fondazione SkyCiv, in accordo con l'equazione 12, calcola il rapporto di utilità flessionale (Equazione 13) prendendo la domanda di flessione rispetto alla capacità di flessione.
\( \testo{Rapporto di utilità} = frac{\testo{Domanda di flessione}}{\testo{Capacità di flessione}} \freccia destra \) Equazione 13
Ulteriori verifiche
Altre verifiche non menzionate dal codice, compresi i controlli della pressione del suolo, sollevamento, e vengono verificati anche altri controlli di stabilità.
Pressione del suolo
La determinazione della pressione di base o dell'interazione tra terreno e plinto si basa principalmente sulle dimensioni del plinto e sulla risultante eccentricità dei carichi applicati. A seconda del posizionamento di questa eccentricità risultante, la pressione alla base può indurre una compressione totale o parziale sul plinto. Questa valutazione consente di verificare se il terreno sottostante è in grado di sostenere la totalità dei carichi trasmessi dal plinto.
Per una guida dettagliata per il calcolo manuale della pressione del suolo, si prega di fare riferimento a questo collegamento: Distribuzione della pressione sotto una base rettangolare di cemento
Il rapporto di utilità viene valutato confrontando la pressione massima del suolo (stato di utilizzabilità) con la capacità portante lorda consentita del terreno:
\( \testo{Rapporto di utilità} = frac{\testo{Max. Pressione del suolo}}{\testo{Capacità portante lorda ammissibile del terreno}} \freccia destra \) Equazione 14
Sollevamento
Verifica il carico assiale determinante agente sul plinto. Somma tutti i carichi verticali compreso il carico dell'utente e i pesi propri della colonna, soletta di fondazione, suolo, e forza di galleggiamento. Se la colonna subisce una forza verso l'alto, i pesi propri specificati devono controbilanciare la forza verso l'alto; altrimenti, il progetto rischia di fallire a causa dell'instabilità.
Ribaltamento
Il ribaltamento del plinto viene verificato sommando tutti i momenti attorno ad un punto del plinto comprese tutte le forze agenti su di esso. Tutte le combinazioni di carico di esercizio devono essere considerate per verificare il momento ribaltante determinante. Generalmente, un fattore di sicurezza pari a 1.5-2 serve per valutare se il basamento supera il controllo di ribaltamento.
Scorrevole
Per verificare lo scorrimento, la somma dei carichi resistenti orizzontali rivolti a destra è divisa per la somma dei carichi rivolti a sinistra.
- Resistere ai carichi:
- Forza orizzontale dovuta all'attrito tra la base del basamento e il terreno della sottostruttura
- Pressione del suolo passiva (se incluso)
- Carichi scorrevoli:
- La componente orizzontale della pressione attiva del suolo
- La componente orizzontale della pressione risultante del sovrapprezzo
Generalmente, un fattore minimo di sicurezza pari a 1.5 si usa. Se sul basamento non agisce alcuna forza orizzontale, non è necessario verificare lo scorrimento.
Modulo di progettazione della Fondazione SkyCiv
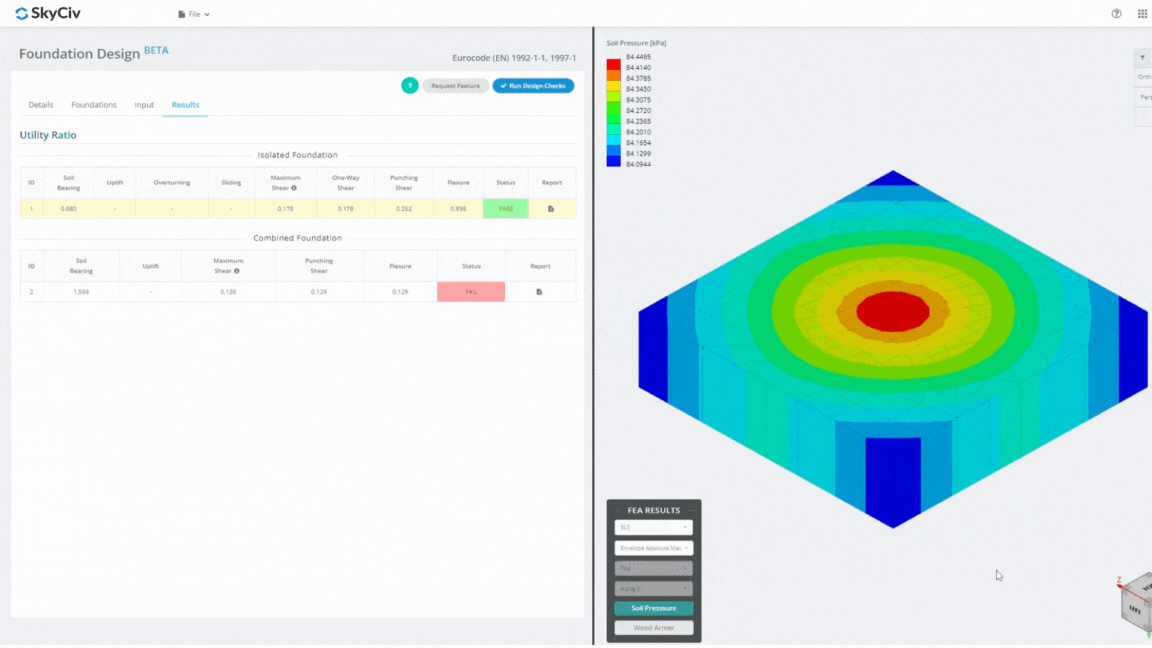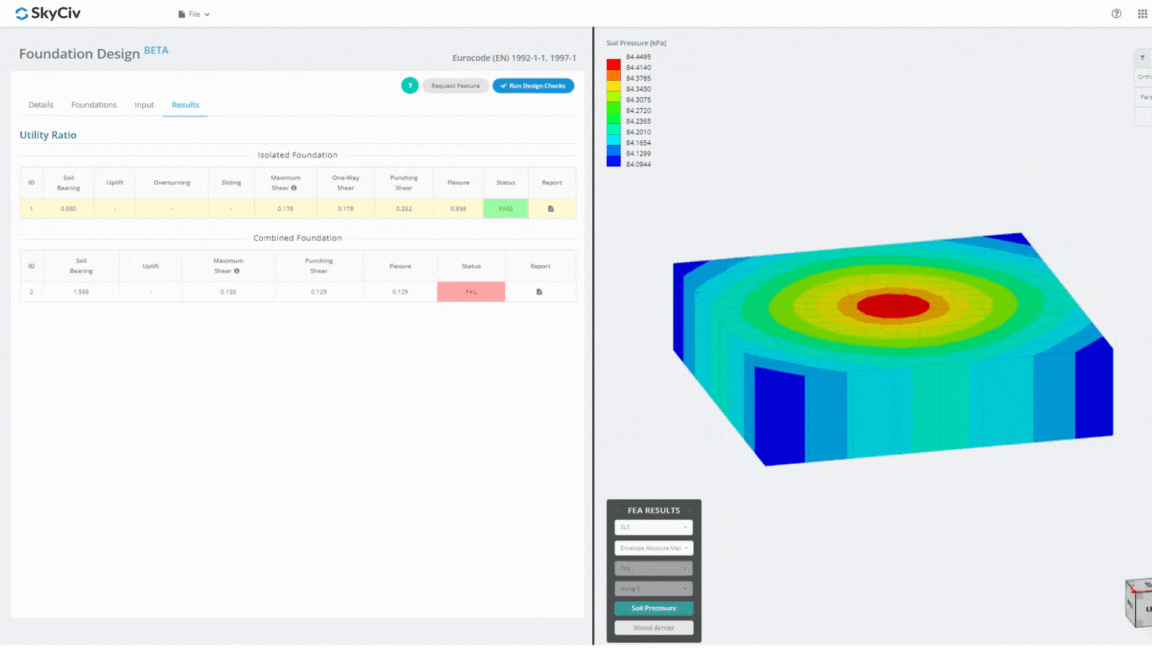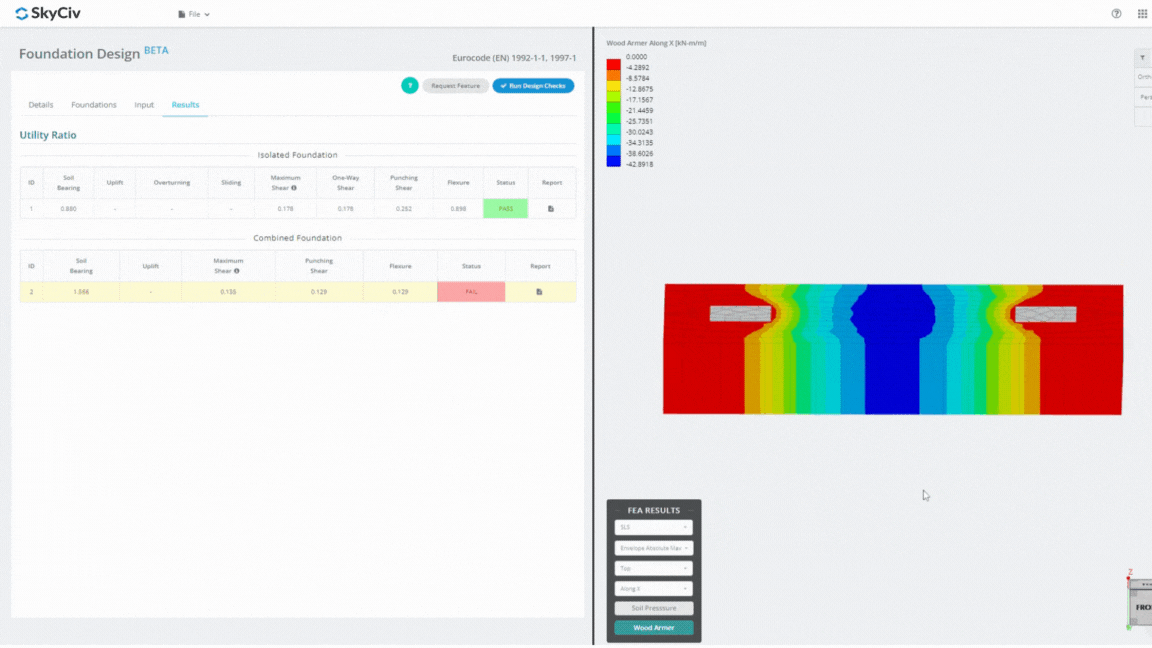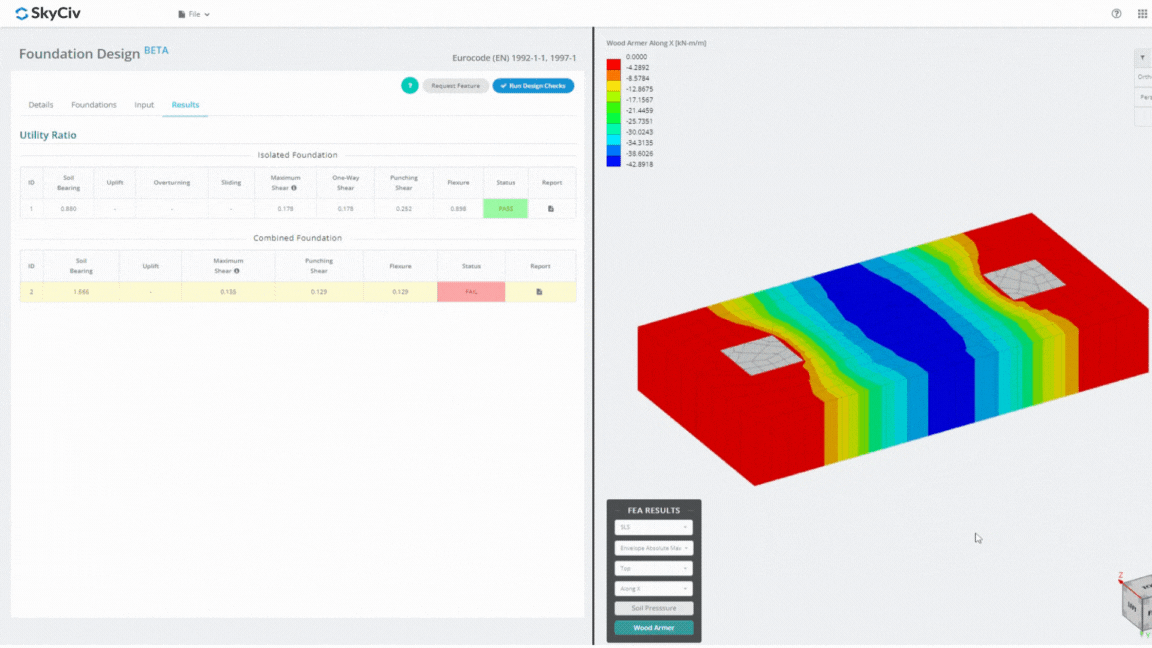
Il Foundation Design Module è un potente strumento integrato con l'analisi degli elementi finiti (BRUTTA), in grado di condurre analisi approfondite della pressione del suolo e del braccio in legno per controlli dettagliati sulla flessione. Esegue tutte le verifiche strutturali previste dall'ACI 318 e altre verifiche sopra menzionate e le presenta in una relazione completa.
Inizia con la Fondazione SkyCiv oggi!
Avvia il Progetto di fondazione e provalo oggi! È facile iniziare, ma se hai bisogno di ulteriore aiuto, quindi assicurati di visitare il nostro documentazione o mettiti in contatto con noi!
Non un utente SkyCiv? Iscriviti per un Gratuito 14 Prova di un giorno per iniziare!
Sviluppatore del prodotto
BSc (Civile), Master (Civile)
Albert Pamonag
Ingegnere strutturale, Sviluppo del prodotto
ME. Ingegneria Civile
Riferimenti
- Requisiti del codice di costruzione per calcestruzzo strutturale (ACI 318-14) Commento ai requisiti del codice edilizio per il calcestruzzo strutturale (ACI 318R-14). American Concrete Institute, 2014.
- McCormac, Jack C., e Russell H. Marrone. Progettazione di ACI in cemento armato 318-11 Code Edition. Wiley, 2014.
- Taylor, Andrea, et al. The Reinforced Concrete Design Handbook: un compagno di ACI-318-14. American Concrete Institute, 2015.




