A Base combinata è un unico basamento che sostiene due o più colonne. I plinti combinati sono comunemente usati quando le colonne sono distanziate troppo vicino, dove due basi isolate non sarebbero soddisfacenti. Per esempio, con due basamenti isolati troppo vicini tra loro, il suolo sottostante può condividere porzioni di zone di influenza, che porta a un'estensione richiesta di uno o di entrambi i plinti isolati. A seconda dei vincoli fisici o di altro tipo, questo potrebbe non essere possibile.
Il modulo SkyCiv Foundation Design include la progettazione di fondazioni combinate conformi all'American Concrete Institute (ACI 318).
Vuoi provare il software Foundation Design di SkyCiv? Il nostro strumento gratuito consente agli utenti di eseguire calcoli di carico senza alcun download o installazione!
Progettazione di una fondazione combinata
Requisiti di dimensione
Per determinare le dimensioni di un basamento isolato, servizio o carichi non fattorizzati, come morto (D), Vivere (L), Vento (W), Sismico (E), ecc. verrà applicato utilizzando Combinazioni di carico, come definito da ACI 318-14. Qualunque combinazione di carico governa sarà considerata il carico di progetto, e viene confrontata con la pressione del suolo ammissibile come mostrato nell'equazione 1, come consigliato in Sezione 13.2.6 of ACI 318-14.
\(\testo{q}_{\testo{un carico}} = frac{ \testo{P1}_{\testo{n}} + \testo{P2}_{\testo{n}} }{\testo{A}} \freccia destra \) Equazione 1
dove:
qun carico = pressione netta ammissibile del suolo
P1n = carichi non fattorizzati alla colonna 1 (sinistra)
P2n = carichi non fattorizzati alla colonna 2 (giusto)
A = Area della fondazione
Dall'equazione 1, qun carico sono interscambio con A.
\(\testo{A} = frac{ \testo{P1}_{\testo{n}} + \testo{P2}_{\testo{n}} }{\testo{q}_{\testo{un carico}}} \freccia destra \) Equazione 1a
A questo punto, le dimensioni del basamento possono essere calcolate a ritroso dalla dimensione dell'area richiesta, A.
Taglio unidirezionale
La Taglio unidirezionale stato limite, conosciuto anche come “taglio flessionale”, estende la sua sezione critica per tutta la larghezza del plinto e si trova a distanza “d” dalla faccia di una colonna, dove si trova Critical Plane Shear (Fare riferimento alla figura 1).
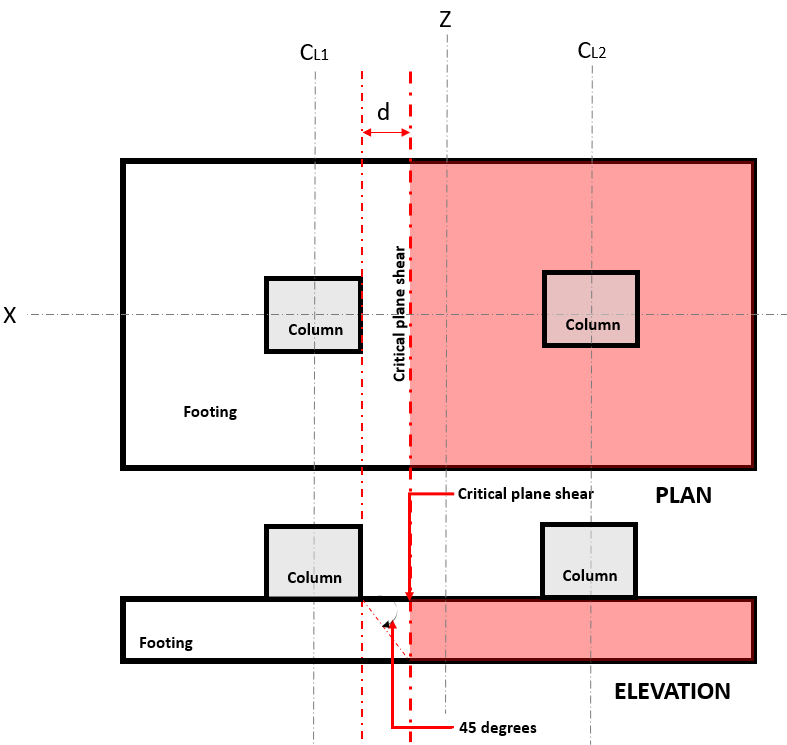
figura 1. Taglio piano critico di taglio unidirezionale
La Senso unico cesoia Richiesta o V u viene calcolato assumendo che la fondazione sia a sbalzo dalla colonna in cui si trova l'area (rosso) indicato in figura 1 secondo ACI 318-14, Sezione 8.5.3.1.1.
La Capacità di taglio unidirezionale o ϕVc è definita come resistenza al taglio finale e calcolata utilizzando l'equazione 2 per ACI 318-14, Sezione 22.5.5.1:
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 2 \sqrt{\testo{f ’}_{\testo{c}}} \volte testo{b}_{\testo{w}} \volte testo{d} \freccia destra \) Equazione 2 (ACI Eq. 22.5.5.1 inglese)
o
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 0.17 \sqrt{\testo{f ’}_{\testo{c}}} \volte testo{b}_{\testo{w}} \volte testo{d} \freccia destra \) Equazione 2 (ACI Eq. 22.5.5.1 metrico)
dove:
ϕcesoia = fattore di progetto di taglio
f’c = resistenza del calcestruzzo specificata, psi o MPa
bw = spessore della fondazione, pollici o mm
d = distanza dalla fibra a compressione estrema al baricentro dell'armatura a trazione longitudinale, pollici o mm
La richiesta di taglio e la capacità di taglio devono soddisfare la seguente equazione per soddisfare i requisiti di progettazione di ACI 318-14:
\(\testo{V }_{\testo{u}} \leq phi text{V }_{\testo{c}} \freccia destra \) Equazione 3 (ACI Eq. 7.5.1.1(b))
Fondazione SkyCiv, in conformità all'equazione 3, calcola il rapporto di unità di taglio unidirezionale (Equazione 4) considerando la domanda di taglio rispetto alla capacità di taglio.
\( \testo{rapporto} = frac{\testo{Shear Demand}}{\testo{Capacità di taglio}} \freccia destra \) Equazione 4
Taglio a due vie
La Taglio a due vie stato limite, conosciuto anche come “punzonatura cesoia”, estende la sua sezione critica ad una distanza “d/2” dalla faccia della colonna e attorno al perimetro della colonna. Il piano di taglio critico si trova in quella sezione del basamento (Fare riferimento alla figura 2).
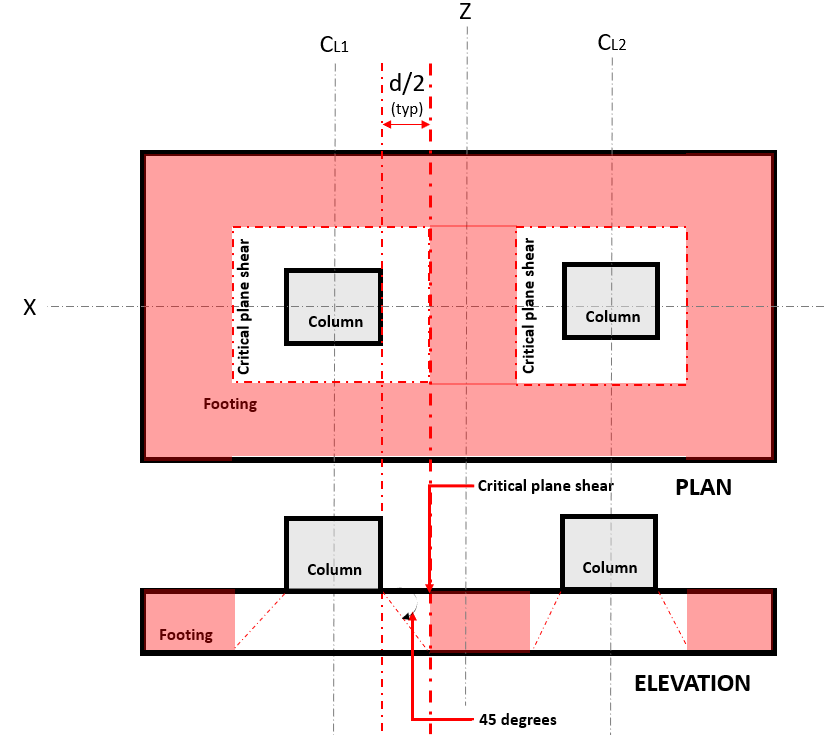
figura 2. Taglio piano critico del taglio bidirezionaleway
La Due stradeascolta la domanda o V u si verifica sul piano di taglio critico, situato ad una distanza di “d/2” dove il (rosso) area tratteggiata, indicato in figura 2, secondo ACI 318-14, Sezione 22.6.4.
La Capacità di taglio o ϕVc è governato dal valore più piccolo calcolato utilizzando Equation 5, 6, e 7 per ACI 318-14, Sezione 22.6.5.2:
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 4 \times lambda times sqrt{\testo{f ’}_{\testo{c}}} \freccia destra \) Equazione 5 (ACI Eq. 22.6.5.2(un carico) inglese)
\(\phi text{V }_{\testo{c}} = sinistra ( 2 + \frac{4}{\beta } \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 6 (ACI Eq. 22.6.5.2(b) inglese)
\(\phi text{V }_{\testo{c}} = sinistra ( 2 + \frac{\alfa _{S} \volte d }{b{Il}} \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 7 (ACI Eq. 22.6.5.2(c) inglese)
o
\(\phi text{V }_{\testo{c}} = phi _{\testo{cesoia}} \volte 0.33 \times lambda times sqrt{\testo{f ’}_{\testo{c}}} \freccia destra \) Equazione 5 (ACI Eq. 22.6.5.2(un carico) metrico)
\(\phi text{V }_{\testo{c}} = 0.17 \volte sinistra ( 1 + \frac{2}{\beta } \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 6 (ACI Eq. 22.6.5.2(b) metrico)
\(\phi text{V }_{\testo{c}} = 0.0083 \volte sinistra ( 2 + \frac{\alfa _{S} \volte d }{b{Il}} \giusto ) \times lambda times sqrt{f’_{c}} \freccia destra \) Equazione 7 (ACI Eq. 22.6.5.2(c) metrico)
Nota: β è il rapporto tra il lato lungo e il lato corto della colonna, carico concentrato, o area di reazione e αS viene data 22.6.5.3
dove:
λ = fattore di modifica per riflettere le proprietà meccaniche ridotte del calcestruzzo leggero rispetto al calcestruzzo normale della stessa resistenza alla compressione
f’c = resistenza del calcestruzzo specificata, psi o MPa
d = distanza dalla fibra a compressione estrema al baricentro dell'armatura a trazione longitudinale, in.o mm
La richiesta di taglio e la capacità di taglio devono soddisfare la seguente equazione per soddisfare i requisiti di progettazione di ACI 318-14:
\(\testo{V }_{\testo{u}} \leq phi text{V }_{\testo{c}} \freccia destra \) Equazione 8 (ACI Eq. 7.5.1.1(b))
Fondazione SkyCiv, in conformità all'equazione 8, calcola il rapporto di unità di taglio a due vie (Equazione 9) considerando la domanda di taglio rispetto alla capacità di taglio.
\( \testo{rapporto} = frac{\testo{Shear Demand}}{\testo{Capacità di taglio}} \freccia destra \) Equazione 9
Flessione
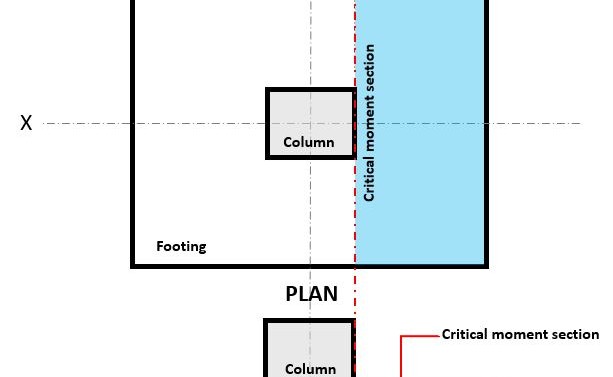
figura 3. Sezione momento critico della flessione
La Flessionale lo stato limite si verifica a la sezione flessione critica, situato sulla faccia della colonna in cima al basamento (Fare riferimento alla figura 3).
La Domanda flessionale, o Mu si trova nella sezione di flessione critica (area blu del tratteggio) indicato in figura 3, e viene calcolato utilizzando l'equazione 10:
\( \testo{M}_{u} = testo{q}_{u} \volte sinistra ( \frac{l_{x}}{2} – \frac{c_{x}}{2} \giusto ) \volte l_{z} \volte sinistra ( \frac{\frac{l_{x}}{2} – \frac{c_{x}}{2} }{2} \giusto ) \freccia destra \) Equazione 10
dove:
qu = pressione del suolo fattorizzata, ksf o kpa
lx = dimensione della fondazione parallela all'asse x, pollici o mm
lz = dimensione della fondazione parallela all'asse z, pollici o mm
cx = dimensione della colonna parallela all'asse x, pollici o mm
La Capacità flessionale, o Mn viene calcolato utilizzando l'equazione 11:
\( \phi text{M}_{n} = phi_{\testo{flessione}} \volte A_{S} \volte f_{y} \volte sinistra( d – \frac{un carico}{2} \giusto) \freccia destra \) Equazione 11
dove:
ϕ = fattore di progettazione flessionale
lx = dimensione della fondazione parallela all'asse x, pollici o mm
lz = dimensione della fondazione parallela all'asse z, pollici o mm
d = distanza dalla fibra a compressione estrema al baricentro dell'armatura a trazione longitudinale, pollici o mm
AS = area di rinforzo, pollici2 o mm2
a = profondità del blocco di sollecitazione rettangolare equivalente, pollici o mm
fy = resistenza dell'acciaio, ksi o MPa
Moment Demand e Moment Capacity devono soddisfare la seguente equazione per soddisfare i requisiti di progettazione di ACI 318-14:
\(\testo{M}_{\testo{u}} \leq phi text{M}_{\testo{n}} \freccia destra \) Equazione 12 (ACI Eq. 7.5.1.1(b))
Fondazione SkyCiv, in conformità all'equazione 12, calcola il rapporto di unità di flessione (Equazione 13) prendendo la domanda di flessione rispetto alla capacità di flessione
\( \testo{rapporto} = frac{\testo{Domanda di flessione}}{\testo{Capacità di flessione}} \freccia destra \) Equazione 13
Albert Pamonag
Ingegnere strutturale, Sviluppo del prodotto
B.S. Ingegneria Civile
Riferimenti
- Requisiti del codice di costruzione per calcestruzzo strutturale (ACI 318-14) Commento ai requisiti del codice edilizio per il calcestruzzo strutturale (ACI 318R-14). American Concrete Institute, 2014.
- McCormac, Jack C., e Russell H. Marrone. Progettazione di ACI in cemento armato 318-11 Code Edition. Wiley, 2014.
- Taylor, Andrea, et al. The Reinforced Concrete Design Handbook: un compagno di ACI-318-14. American Concrete Institute, 2015.



