Esempio di progettazione della piastra di base utilizzando AS 4100:2020 e come 3600:2018
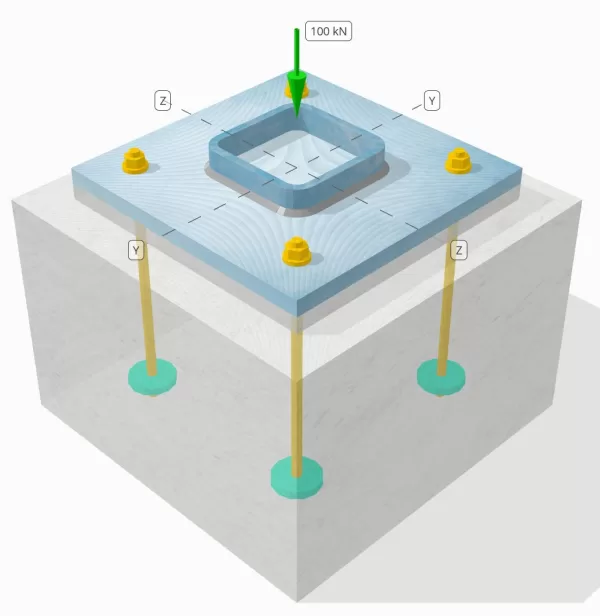
Dichiarazione del problema
Determina se la connessione a piastra da colonna a base progettata è sufficiente per un carico di compressione da 100 kn.
Dati dati
Colonna:
Sezione colonna: 50×10 SHS
Area colonna: 5260 mm2
Materiale colonna: AS / NZS 1163 Gr. C350
Piastra di base:
Dimensioni della piastra di base: 350 mm x 350 mm
Spessore della piastra di base: 20 mm
Materiale della piastra di base: AS / NZS 3678 Gr. C250
Malta:
Spessore di malta: 20 mm
Calcestruzzo:
Dimensioni concrete: 450 mm x 450 mm
Spessore di cemento: 300 mm
Materiale di cemento: N28
saldature:
Dimensione della saldatura: 6 mm
Classificazione del metallo di riempimento: E43xx
Carico di compressione trasferito solo attraverso saldature? SÌ
Modello nello strumento gratuito SkyCiv
Modella il design della piastra di base qui sopra utilizzando il nostro strumento online gratuito oggi stesso! Non è richiesta la registrazione.
Calcoli passo-passo
Dai un'occhiata #1: Calcolare la capacità portante del calcestruzzo
Iniziare, Determiniamo il aree cuscinetti per AS 3600:2018 Clausola 12.6:
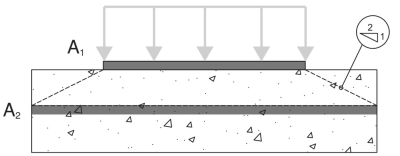
A1 - Area del cuscinetto della piastra di base
A2 - Area di supporto in cemento, Proiettato a a 2:1 pendenza
\(
A_1 = l_{p.p} B_{p.p} = 350 \, \testo{mm} \volte 350 \, \testo{mm} = 122500 \, \testo{mm}^ 2
\)
\(
A_2 = n_{A2} B_{A2} = 450 \, \testo{mm} \volte 450 \, \testo{mm} = 202500 \, \testo{mm}^ 2
\)
Da li, calcoliamo il capacità portante del calcestruzzo, espressa come forza equivalente. Usiamo Guida alla progettazione ASI 07 1sto Ed. Sezione 9.1 come riferimento.
\(
\phi N_c = min sinistra( \phi 0.9 \sinistra( f’_c giusto) A_1 sqrt{\frac{A_2}{A_1}}, \phi 1.8 \sinistra( f’_c giusto) A_1 a destra)
\)
\(
\phi N_c = min sinistra( 0.6 \volte 0.9 \volte sinistra( 28 \, \testo{MPa} \giusto) \volte 122500 \, \testo{mm}^2 volte sqrt{\frac{202500 \, \testo{mm}^ 2}{122500 \, \testo{mm}^ 2}}, 0.6 \volte 1.8 \volte sinistra( 28 \, \testo{MPa} \giusto) \volte 122500 \, \testo{mm}^2 a destra)
\)
\(
\phi N_c = 2381.4 \, \testo{kN}
\)
Da 100 kN <2381.4 kN, il la capacità portante del calcestruzzo è sufficiente.
Dai un'occhiata #2: Calcola la capacità di saldatura
Per valutare la capacità di saldatura, Determiniamo prima il lunghezza totale della saldatura Basato sulle dimensioni della colonna:
\(
L_{\testo{saldare}} = 2 \sinistra( b_{\testo{col}} – 2 r_{\testo{col}} – 2 t_{\testo{col}} \giusto) + 2 \sinistra( d_{\testo{col}} – 2 r_{\testo{col}} – 2 t_{\testo{col}} \giusto)
\)
\(
L_{\testo{saldare}} = 2 \volte sinistra( 150 \, \testo{mm} – 2 \volte 15 \, \testo{mm} – 2 \volte 10 \, \testo{mm} \giusto) + 2 \volte sinistra( 150 \, \testo{mm} – 2 \volte 15 \, \testo{mm} – 2 \volte 10 \, \testo{mm} \giusto) = 400 \, \testo{mm}
\)
Con questo, Possiamo calcolare il sollecitazione per unità di lunghezza della saldatura, Supponendo il 100 Il carico kN è distribuito uniformemente:
\(
v^*_w = frac{N_x}{L_{\testo{saldare}}} = frac{100 \, \testo{kN}}{400 \, \testo{mm}} = 0.25 \, \testo{metri ed è fissato alla base e fissato in alto}
\)
Dopo di che, Determiniamo il capacità di saldatura per unità di lunghezza usando AS 4100:2020 Clausola 9.6.3.10:
\(
\phi v_w = phi 0.6 f_{il tuo} E_w k_r = 0.8 \volte 0.6 \volte 430 \, \testo{MPa} \volte 4.243 \, \testo{mm} \volte 1 = 0.87576 \, \testo{metri ed è fissato alla base e fissato in alto}
\)
Da 0.87576 metri ed è fissato alla base e fissato in alto < 0.25 metri ed è fissato alla base e fissato in alto, il la capacità di saldatura è sufficiente.
Dai un'occhiata #3: Calcola la capacità di cedimento della flessione della piastra di base dovuta al carico di compressione
La capacità di flessione della piastra di base dipende dalle sue dimensioni. Se il piatto è troppo largo, richiederà materiale più spesso. La selezione della dimensione della piastra di base giusta per un determinato carico richiede esperienza, e l'esecuzione di più calcoli può richiedere molto tempo. La Software di progettazione della piastra di base Skyciv semplifica questo processo, Abilitare modellazione e analisi veloci ed efficienti in soli secondi.
Usiamo Guida alla progettazione ASI 07, 1prima edizione., tavolo 7 per verificare la capacità di snervamento flessionale della piastra di base. Primo, Determiniamo il kx fattore.
\(
k_x = 1.65 \sinistra( \frac{\sqrt{L_{p.p} B_{p.p}}}{b_{\testo{col}}} \giusto) = 1.65 \volte sinistra( \frac{\sqrt{350 \, \testo{mm} \volte 350 \, \testo{mm}}}{150 \, \testo{mm}} \giusto) = 3.85
\)
Successivamente, calcoliamo la resistenza portante del calcestruzzo in termini di sollecitazione sull'area. Fare riferimento a Dai un'occhiata #1 per la capacità portante calcolata.
\(
\phi f_b = frac{\phi N_c}{L_{p.p} B_{p.p}} = frac{2381.4 \, \testo{kN}}{350 \, \testo{mm} \volte 350 \, \testo{mm}} = 19.44 \, \testo{MPa}
\)
Utilizziamo quindi questo valore per ottenere il X fattore.
\(
X = frac{4 N_c^*}{\phi f_b (2 b_{\testo{col}})^ 2} = frac{4 \volte 100 \, \testo{kN}}{19.44 \, \testo{MPa} \volte (2 \volte 150 \, \testo{mm})^ 2} = 0.22862
\)
Adesso, usiamo il calcolato kx e X fattori per valutare la λ (lambda) fattore.
\(
\lambda = min sinistra( \frac{k_x sqrt{X}}{1 + \sqrt{1 – X}}, 1.0 \giusto) = min sinistra( \frac{3.85 \volte sqrt{0.22862}}{1 + \sqrt{1 – 0.22862}}, 1 \giusto) = 0.98008
\)
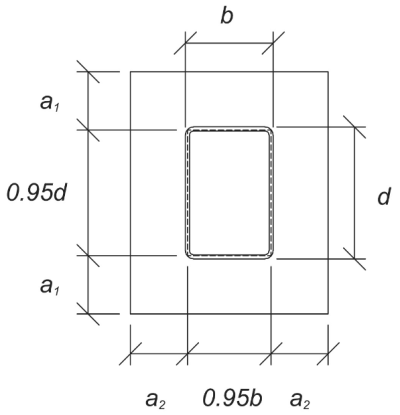
Calcoliamo quindi la lunghezza della trave a sbalzo della piastra di base sottoposta al carico del cuscinetto. Secondo Guida alla progettazione ASI 07, 1prima edizione., sezioni 6.1 e 9.1–9.2, la lunghezza del cantilever è come mostrato:
\(
l = max sinistra( \frac{L_{p.p} – 0.95 d_{\testo{col}}}{2}, \frac{B_{p.p} – 0.95 b_{\testo{col}}}{2}, \lambda 0.306 \sqrt{d_{\testo{col}} b_{\testo{col}}} \giusto)
\)
\(
l = max sinistra( \frac{350 \, \testo{mm} – 0.95 \volte 150 \, \testo{mm}}{2}, \frac{350 \, \testo{mm} – 0.95 \volte 150 \, \testo{mm}}{2}, 0.98008 \volte 0.306 \volte sqrt{150 \, \testo{mm} \volte 150 \, \testo{mm}} \giusto)
\)
\(
l = 103.75 \, \testo{mm}
\)
Considerando questa sezione critica della piastra di base, calcoliamo lo sforzo di snervamento flessionale. Questa è un'equazione riorganizzata da Guida alla progettazione ASI 07, 1prima edizione., Sezione 9.2, con riferimento a Sezione 6.1.
\(
f^* = frac{2 N_xl^2}{B_{p.p} L_{p.p} (t_{p.p})^ 2}
\)
\(
f^* = frac{2 \volte 100 \, \testo{kN} \volte 103.75 \, \testo{mm}^ 2}{350 \, \testo{mm} \volte 350 \, \testo{mm} \volte (20 \, \testo{mm})^ 2} = 43.935 \, \testo{MPa}
\)
Il passaggio finale consiste nel calcolare la capacità di snervamento della piastra di base utilizzando AS 4100:2020, Clausola 5.2.1.
\(
\phi f_y = phi f_{y_{p.p}} = 0.9 \volte 250 \, \testo{MPa} = 225 \, \testo{MPa}
\)
Da 43.935 MPa < 225 MPa, il la capacità di flessione della piastra di base è sufficiente.
Riepilogo del progetto
Il software di progettazione della piastra di base Skyciv può generare automaticamente un rapporto di calcolo passo-passo per questo esempio di progettazione. Fornisce inoltre un riepilogo dei controlli eseguiti e dei loro rapporti risultanti, rendere le informazioni facili da capire a colpo d'occhio. Di seguito è riportata una tabella di riepilogo del campione, che è incluso nel rapporto.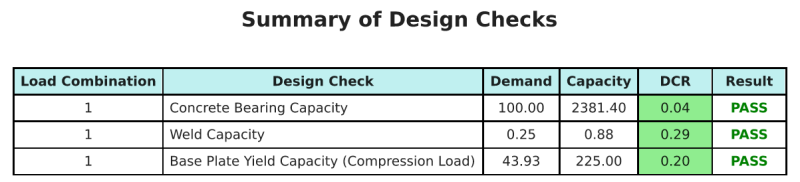
Rapporto campione Skyciv
Scopri il livello di dettaglio e chiarezza che puoi aspettarti da un rapporto sulla progettazione della piastra base SkyCiv. Il rapporto include tutti i controlli chiave della progettazione, equazioni, e i risultati presentati in un formato chiaro e di facile lettura. È pienamente conforme agli standard di progettazione. Fare clic di seguito per visualizzare un rapporto di esempio generato utilizzando il calcolatore della piastra di base SkyCiv.
Acquista software di base
Acquista da solo la versione completa del modulo di progettazione della piastra di base senza altri moduli SkyCiv. Questo ti dà un set completo di risultati per la progettazione della piastra di base, tra cui report dettagliati e più funzionalità.


