Esempio di design della piastra di base usando EN 1993-1-8-2005, NEL 1993-1-1-2005 e e 1992-1-1-2004
Dichiarazione del problema:
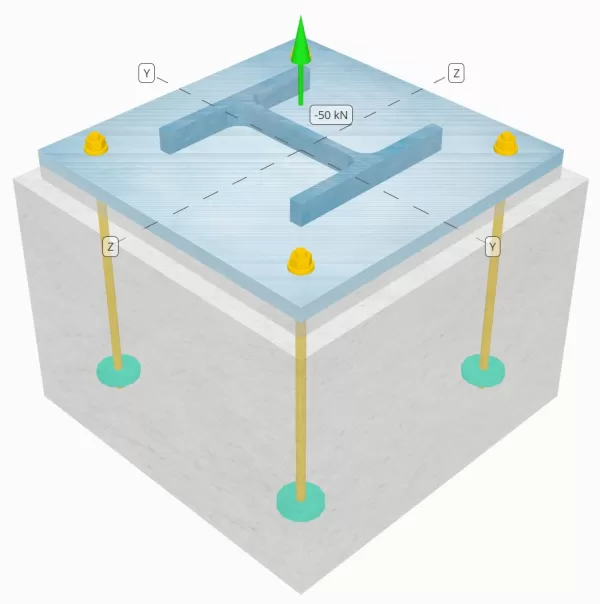
Determina se la connessione a piastra da colonna a base progettata è sufficiente per un carico di tensione da 50 kn.
Dati dati:
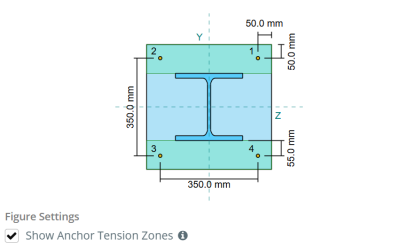
Colonna:
Sezione colonna: LUI 240 B
Area colonna: 10600 mm2
Materiale colonna: S235
Piastra di base:
Dimensioni della piastra di base: 450 mm x 450 mm
Spessore della piastra di base: 20 mm
Materiale della piastra di base: S235
Malta:
Spessore di malta: 20 mm
Calcestruzzo:
Dimensioni concrete: 500 mm x 500 mm
Spessore di cemento: 350 mm
Materiale di cemento: C25/30
Crackato o non collocato: Rotto
Ancore:
Diametro dell'ancora: 12 mm
Efficace lunghezza dell'incorporamento: 300.0 mm
Diametro della piastra incorporato: 60 mm
Spessore della piastra incorporata: 10 mm
Materiale di ancoraggio: 8.8
Altre informazioni:
- Ancore non concountersunk.
- Ancora con fili tagliati.
saldature:
Tipo di saldatura: Fpbw
Classificazione del metallo di riempimento: E35
Dati di ancoraggio (a partire dal Calcolatore Skyciv):
Definizioni:
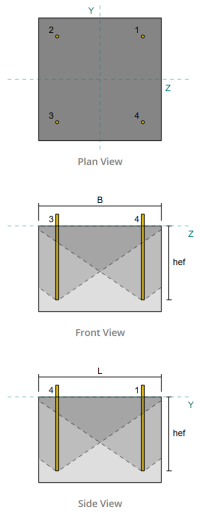
Zona di tensione di ancoraggio:
Nel Software di progettazione della piastra di base Skyciv, solo ancore situati all'interno del zona di tensione di ancoraggio sono considerati efficaci nel resistere al sollevamento. Questa zona include in genere le aree vicino alle flange di colonna o al web. Le ancore al di fuori di questa zona non contribuiscono alla resistenza alla tensione e sono esclusi dai calcoli di sollevamento.
L'Assunzione semplifica l'analisi della piastra di base approssimando il modo in cui la forza di sollevamento si diffonde attraverso la piastra.
Gruppi di ancoraggio:
La Software di progettazione della piastra di base Skyciv Include una caratteristica intuitiva che identifica quali ancore fanno parte di un gruppo di ancoraggio per la valutazione rottura concreta e Blowout della faccia laterale in cemento fallimenti.
Un gruppo di ancoraggio è costituito da più ancore con profondità di incorporamento e spaziatura simili, e sono abbastanza vicini che il loro Le aree di resistenza proiettate si sovrappongono. Quando le ancore sono raggruppate, Le loro capacità sono combinate per resistere alla forza di tensione totale applicata al gruppo.
Le ancore che non soddisfano i criteri di raggruppamento sono trattati come ancore singole. In questo caso, Solo la forza di tensione sull'ancoraggio individuale è controllata contro la propria area di resistenza efficace.
Calcoli passo-passo:
Dai un'occhiata #1: Calcola la capacità di saldatura
Dalle informazioni fornite, La saldatura utilizzata in questo esempio di design è un Saldatura a testa di penetrazione completa (Fpbw). Calcoleremo le capacità metalliche di base della colonna e la piastra di base per determinare la resistenza alla saldatura. Per fare questo, dobbiamo prima calcolare il lunghezza totale della saldatura sulla colonna e ottenere lo stress di saldatura.
\(
F_{w,Ed} = frac{N_x}{2 b_f t_f + \sinistra( d_{col} – 2 t_f – 2 r_{col} \giusto) t_w}
\)
\(
F_{w,Ed} = frac{50 \, \testo{kN}}{2 \volte 240 \, \testo{mm} \volte 17 \, \testo{mm} + \sinistra( 240 \, \testo{mm} – 2 \volte 17 \, \testo{mm} – 2 \volte 21 \, \testo{mm} \giusto) \volte 10 \, \testo{mm}} = 5.102 \, \testo{MPa}
\)
Successivamente, Determiniamo il resistenza alla trazione del materiale più debole tra la colonna e la piastra di base.
\(
f_y = \min \left( f_{y,\testo{col}}, f_{y,\testo{p.p}} \giusto) = min sinistra( 225 \, \testo{MPa}, 225 \, \testo{MPa} \giusto) = 225 \, \testo{MPa}
\)
Quindi usiamo NEL 1993-1-8:2005 Clausola 4.7.1 e NEL 1993-1-1:2005 Eq. 6.6 Per calcolare la resistenza alla saldatura del design FPBW.
\(
F_{w,Rd3} = frac{f_y}{\Per calcolarlo{M0}} = frac{225 \, \testo{MPa}}{1} = 225 \, \testo{MPa}
\)
Da 5.102 MPa < 225 MPa, La capacità di saldatura è sufficiente.
Dai un'occhiata #2: Calcola la capacità di cedimento della flessione della piastra di base dovuta al carico di tensione
Per calcolare il Capacità di flessione della piastra di base contro il carico di tensione, noi useremo schemi di linea di rendimento come motivi circolari e motivi non circolari. Poi, Determiniamo la capacità di governo, Supponendo che nessuna forza indiscreta, Confrontando la resistenza alla produzione della piastra con la resistenza alla trazione dei bulloni di ancoraggio.
Iniziare, calcoliamo il richiesto dimensioni Basato sul layout del bullone dato. Fare riferimento a NEL 1992-1-8:2005 tavolo 6.2 per guida.
\(
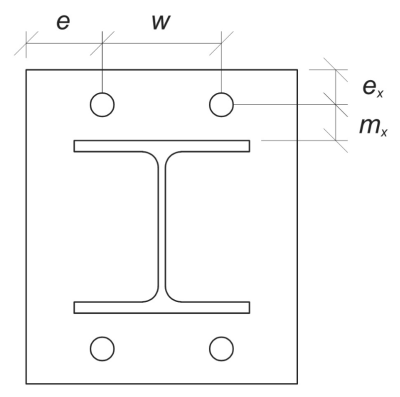
m_x = \frac{S_ – d_{col}}{2} = frac{350 \, \testo{mm} – 240 \, \testo{mm}}{2} = 55 \, \testo{mm}
\)
\(
w = s_z \left( N_{un carico,\testo{lato}} – 1 \giusto) = 350 \, \testo{mm} \volte sinistra( 2 – 1 \giusto) = 350 \, \testo{mm}
\)
\(
e_x = \frac{L_{p.p} – S_}{2} = frac{450 \, \testo{mm} – 350 \, \testo{mm}}{2} = 50 \, \testo{mm}
\)
\(
[object Window]{B_{p.p} – w}{2} = frac{450 \, \testo{mm} – 350 \, \testo{mm}}{2} = 50 \, \testo{mm}
\)
\(
b_p = b_{p.p} = 450 \, \testo{mm}
\)
Calcoliamo anche la distanza del bordo di ancoraggio sulla piastra di base, che è limitato dal \( m_x \) dimensione per
\(
n = \min \left( ex, 1.25 m_x \right) = min sinistra( 50 \, \testo{mm}, 1.25 \volte 55 \, \testo{mm} \giusto) = 50 \, \testo{mm}
\)
Poi, Calcoliamo le lunghezze effettuate del seguente motivi circolari (fare riferimento a Tabella Sci P398 5.3).
Pattern circolare 1:
\(
l_{eff,CP1} = n_{un carico,\testo{lato}} \pi m_x = 2 \times \pi \times 55 \, \testo{mm} = 345.58 \, \testo{mm}
\)
Pattern circolare 2:
\(
l_{eff,CP2} = sinistra( \frac{N_{un carico,\testo{lato}}}{2} \giusto) (\pi m_x + 2 ex) = sinistra( \frac{2}{2} \giusto) \volte (\pi \times 55 \, \testo{mm} + 2 \volte 50 \, \testo{mm}) = 272.79 \, \testo{mm}
\)
Studio circolare che governa lunghezza effettiva:
\(
l_{eff,cp} = \min (l_{eff,CP1}, l_{eff,CP2}) = \min (345.58 \, \testo{mm}, 272.79 \, \testo{mm}) = 272.79 \, \testo{mm}
\)
Adesso, calcoliamo le lunghezze effettuazioni di quanto segue Modelli non circolari (fare riferimento a Tabella Sci P398 5.3)
Pattern non circolare 1:
\(
l_{eff,NC1} = frac{B_P}{2} = frac{450 \, \testo{mm}}{2} = 225 \, \testo{mm}
\)
Pattern non circolare 2:
\(
l_{eff,NC2} = sinistra( \frac{N_{un carico,\testo{lato}}}{2} \giusto) (4 m_x + 1.25 ex) = sinistra( \frac{2}{2} \giusto) \volte (4 \volte 55 \, \testo{mm} + 1.25 \volte 50 \, \testo{mm}) = 282.5 \, \testo{mm}
\)
Pattern non circolare 3:
\(
l_{eff,NC3} = 2 m_x + 0.625 ex + e = 2 \volte 55 \, \testo{mm} + 0.625 \volte 50 \, \testo{mm} + 50 \, \testo{mm} = 191.25 \, \testo{mm}
\)
Pattern non circolare 4:
\(
l_{eff,NC4} = 2 m_x + 0.625 ex + \frac{(N_{un carico,\testo{lato}} – 1) s_z}{2} = 2 \volte 55 \, \testo{mm} + 0.625 \volte 50 \, \testo{mm} + \frac{(2 – 1) \volte 350 \, \testo{mm}}{2} = 316.25 \, \testo{mm}
\)
Direzione del modello non circolare lunghezza effettiva:
\(
l_{eff,nc} = \min (l_{eff,NC1}, l_{eff,NC2}, l_{eff,NC3}, l_{eff,NC4}) = \min (225 \, \testo{mm}, 282.5 \, \testo{mm}, 191.25 \, \testo{mm}, 316.25 \, \testo{mm}) = 191.25 \, \testo{mm}
\)
Poi, Determiniamo il valore inferiore tra le lunghezze efficaci dei motivi circolari e non circolari.
\(
l_{eff,1} = \min (l_{eff,cp}, l_{eff,nc}) = \min (272.79 \, \testo{mm}, 191.25 \, \testo{mm}) = 191.25 \, \testo{mm}
\)
Adesso, Usiamo questa lunghezza effettiva calcolata per calcolare la sua resistenza alla flessione. Secondo NEL 1993-1-8:2005 tavolo 6.2, La resistenza del momento della piastra per la modalità di guasto 1 è:
\(
M_{Resistenza della sezione in compressione,1,Rd} = frac{0.25 l_{eff,1} (t_{p.p})^2 f_{e _bp}}{\Per calcolarlo{M0}} = frac{0.25 \volte 191.25 \, \testo{mm} \volte (20 \, \testo{mm})^2 \times 225 \, \testo{MPa}}{1} = 4303.1 \, \testo{kN} \cdot \text{mm}
\)
Supponendo Nessun indispensatura, Usiamo en 1993-1-8:2005 tavolo 6.2 per determinare il design Resistenza della piastra di base per fallimento Modalità 1 e 2.
\(
F_{T,1,Rd} = frac{2 M_{Resistenza della sezione in compressione,1,Rd}}{m_x} = frac{2 \volte 4303.1 \, \testo{kN} \cdot \text{mm}}{55 \, \testo{mm}} = 156.48 \, \testo{kN}
\)
Poi, calcoliamo la resistenza alla trazione dell'asta di ancoraggio usando NEL 1992-4:2018 Clausola 7.2.1.3. Ciò sarà ulteriormente dettagliato nei controlli di ancoraggio successivi.
\(
F_{t,Rd} = frac{c k_2 f_{u _anc} Come}{\Per calcolarlo{M2, ancora}} = frac{0.85 \volte 0.9 \volte 800 \, \testo{MPa} \volte 113.1 \, \testo{mm}^ 2}{1.25} = 55.372 \, \testo{kN}
\)
Useremo quindi la resistenza per canna di ancoraggio per calcolare il Resistenza del design della piastra di base sotto fallimento Modalità 3, che è il guasto totale del bullone.
\(
F_{T,3,Rd} = n_{un carico,lato} F_{t,Rd} = 2 \volte 55.372 \, \testo{kN} = 110.74 \, \testo{kN}
\)
Infine, Determiniamo il valore di resistenza al governo tra le modalità di guasto.
\(
F_{T,Rd} = \min (F_{T,1,Rd}, F_{T,3,Rd}) = \min (156.48 \, \testo{kN}, 110.74 \, \testo{kN}) = 110.74 \, \testo{kN}
\)
Calcolare il Carico di tensione per flangia, noi abbiamo:
\(
F_{T,Ed} = frac{N_x}{2} = frac{50 \, \testo{kN}}{2} = 25 \, \testo{kN}
\)
Da 25 kN < 110.74 kN, La capacità di cessione di flessione della piastra di base è sufficiente.
Dai un'occhiata #3: Calcola la capacità di trazione dell'asta di ancoraggio
Conosciamo già il valore per la capacità di trazione dell'asta di ancoraggio, Ma affrontiamolo in modo più dettagliato.
Primo, Calcoliamo l'area di sollecitazione di trazione dell'asta di ancoraggio.
\(
A_s = frac{\pi}{4} (d_{anc})^2 = frac{\pi}{4} \volte (12 \, \testo{mm})^2 = 113.1 \, \testo{mm}^ 2
\)
Poi, Applichiamo i valori per il \( c \) fattore e il \( Eurocodice di design con piastra di base in acciaio{2} \) fattore. Questi valori possono essere modificati nelle impostazioni del software di progettazione della piastra di base Skyciv. Prova la versione gratuita qui.
- \( c = 0.85 \) per ancore con fili tagliati
- \( Eurocodice di design con piastra di base in acciaio{2} = 0.9\) per ancora non countersunk
Adesso, Usiamo NEL 1992-4:2018 Clausola 7.2.1.3 per calcolare il Resistenza del design dell'asta di ancoraggio in tensione.
\(
N_{Rd,S} = frac{c k_2 f_{u _anc} Come}{\Per calcolarlo{M2, ancora}} = frac{0.85 \volte 0.9 \volte 800 \, \testo{MPa} \volte 113.1 \, \testo{mm}^ 2}{1.25} = 55.372 \, \testo{kN}
\)
Calcolare il carico di tensione per ancoraggio, noi abbiamo:
\(
N_{Ed} = frac{N_x}{N_{un carico,t}} = frac{50 \, \testo{kN}}{4} = 12.5 \, \testo{kN}
\)
Da 12.5 kN < 55.372 kN, La capacità di trazione dell'asta di ancoraggio è sufficiente.
Dai un'occhiata #4: Calcola la capacità di breakout del calcestruzzo in tensione
Prima di calcolare la capacità di breakout, dobbiamo prima determinare se il membro si qualifica come a membro stretto. Secondo NEL 1992-4:2008 Clausola 7.2.1.4(8), Il membro soddisfa i criteri per un membro ristretto. Pertanto, un carico modificato Efficace lunghezza dell'incorporamento deve essere utilizzato nei calcoli della capacità di breakout. Questa regolazione influisce anche spaziatura caratteristica e Distanza del bordo caratteristico, che deve essere modificato di conseguenza.
Basato sui criteri dei membri stretti, il valori modificati Per il gruppo di ancoraggio sono i seguenti:
- Lunghezza di incorporamento efficace modificata, \( H'_{ef} = 100 mm \)
- spaziatura caratteristica modificata, \( S'_{cr} = 300 mm\)
- Distanza del bordo caratteristico modificato, \( C'_{cr} = 150 mm\)
Usando NEL 1992-4:2018 Eq. 7.3, calcoliamo il Riferimento area di cono in cemento proiettato per un'unica ancora.
\(
A0_{c,N} = S’_{cr,G1} S'_{cr,G1} = 350 \, \testo{mm} \volte 350 \, \testo{mm} = 122500 \, \testo{mm}^ 2
\)
Allo stesso modo, calcoliamo il Area di cono in cemento realizzato effettivo del gruppo di ancoraggio.
\(
UN_{Nc} = L_{Nc} B_{Nc} = 500 \, \testo{mm} \volte 500 \, \testo{mm} = 250000 \, \testo{mm}^ 2
\)
Dove,
\(
L_{Nc} = min sinistra( c_{sinistra,G1}, C'_{cr,G1} \giusto)
+ \sinistra( \min \left( S_{somma,z,G1}, S'_{cr,G1} \sinistra( N_{z,G1} – 1 \giusto) \giusto) \giusto)
+ \min \left( c_{giusto,G1}, C'_{cr,G1} \giusto)
\)
\(
L_{Nc} = min sinistra( 75 \, \testo{mm}, 175 \, \testo{mm} \giusto)
+ \sinistra( \min \left( 350 \, \testo{mm}, 350 \, \testo{mm} \volte (2 – 1) \giusto) \giusto)
+ \min \left( 75 \, \testo{mm}, 175 \, \testo{mm} \giusto)
\)
\(
L_{Nc} = 500 \, \testo{mm}
\)
\(
B_{Nc} = min sinistra( c_{superiore,G1}, C'_{cr,G1} \giusto)
+ \sinistra( \min \left( S_{somma,y,G1}, S'_{cr,G1} \sinistra( N_{y,G1} – 1 \giusto) \giusto) \giusto)
+ \min \left( c_{parte inferiore,G1}, C'_{cr,G1} \giusto)
\)
\(
B_{Nc} = min sinistra( 75 \, \testo{mm}, 175 \, \testo{mm} \giusto)
+ \sinistra( \min \left( 350 \, \testo{mm}, 350 \, \testo{mm} \volte (2 – 1) \giusto) \giusto)
+ \min \left( 75 \, \testo{mm}, 175 \, \testo{mm} \giusto)
\)
\(
B_{Nc} = 500 \, \testo{mm}
\)
Successivamente, Valutiamo il forza caratteristica di un singolo ancoraggio usando NEL 1992-4:2018 Eq. 7.2
\(
N0_{controllare la capacità degli ancoraggi,c} = k_1 \sqrt{\frac{f_{Eurocodice di design con piastra di base in acciaio}}{\testo{MPa}}} \sinistra( \frac{H'_{ef,G1}}{\testo{mm}} \giusto)^{1.5} N
\)
\(
N0_{controllare la capacità degli ancoraggi,c} = 8.9 \volte sqrt{\frac{25 \, \testo{MPa}}{1 \, \testo{MPa}}} \volte sinistra( \frac{116.67 \, \testo{mm}}{1 \, \testo{mm}} \giusto)^{1.5} \volte 0.001 \, \testo{kN} = 56.076 \, \testo{kN}
\)
Dove,
- \(Eurocodice di design con piastra di base in acciaio{1} = 8.9\) per ancore gettate
Adesso, Valutiamo gli effetti della geometria calcolando il necessario parametri per la resistenza di breakout.
La distanza del bordo più breve del gruppo di ancoraggio è determinata come:
\(
c_{min,N} = min sinistra( c_{sinistra,G1}, c_{giusto,G1}, c_{superiore,G1}, c_{parte inferiore,G1} \giusto)
= min sinistra( 87.5 \, \testo{mm}, 87.5 \, \testo{mm}, 150 \, \testo{mm}, 150 \, \testo{mm} \giusto)
= 87.5 \, \testo{mm}
\)
Secondo NEL 1992-4:2018 Eq. 7.4, Il valore per il parametro contabile per la distribuzione dello stress nel calcestruzzo è:
\(
\Psi_{S,N} = min sinistra( 0.7 + 0.3 \sinistra( \frac{c_{min,N}}{C'_{cr,G1}} \giusto), 1.0 \giusto)
= min sinistra( 0.7 + 0.3 \volte sinistra( \frac{75 \, \testo{mm}}{175 \, \testo{mm}} \giusto), 1 \giusto)
= 0.82857
\)
La Effetto di spalling con shell è tenuto conto dell'utilizzo NEL 1992-4:2018 Eq. 7.5, dando:
\(
\Psi_{controllare la capacità degli ancoraggi,N} = min sinistra( 0.5 + \frac{H'_{ef,G1}}{\testo{mm} \, / \, 200}, 1.0 \giusto)
= min sinistra( 0.5 + \frac{116.67 \, \testo{mm}}{1 \, \testo{mm} \, / \, 200}, 1 \giusto)
= 1
\)
Inoltre, entrambi i fattore di eccentricità che per il fattore di influenza della compressione sono presi come:
\(
\Psi_{ec,N} = 1
\)
\(
\Psi_{M,N} = 1
\)
Combiniamo quindi tutti questi fattori e applichiamo AS 5216:2021 Equazione 6.2.3.1 per valutare il Design Resistenza di breakout del cono in cemento per il gruppo di ancoraggio:
\(
N_{Rd,c} = frac{N0_{controllare la capacità degli ancoraggi,c} \sinistra( \frac{UN_{Nc}}{A0_{c,N}} \giusto) \Psi_{S,N} \Psi_{controllare la capacità degli ancoraggi,N} \Psi_{ec,N} \Psi_{M,N}}{\Per calcolarlo{Mc}}
\)
\(
N_{Rd,c} = frac{56.076 \, \testo{kN} \volte sinistra( \frac{250000 \, \testo{mm}^ 2}{122500 \, \testo{mm}^ 2} \giusto) \volte 0.82857 \volte 1 \volte 1 \volte 1}{1.5} = 63.215 \, \testo{kN}
\)
La carico di tensione applicabile totale Sul gruppo di ancoraggio viene calcolato moltiplicando il carico di tensione per ancoraggio per il numero di ancoraggi:
\(
N_{fa} = sinistra( \frac{N_x}{N_{un carico,t}} \giusto) N_{un carico,G1} = sinistra( \frac{50 \, \testo{kN}}{4} \giusto) \volte 4 = 50 \, \testo{kN}
\)
Da 50 kN < 63.215 kN La capacità di breakout in cemento è sufficiente.
Dai un'occhiata #5: Calcola la capacità di estrazione dell'ancoraggio
La Capacità di estrazione di un'ancora è governato dalla resistenza alla sua fine incorporata. Iniziare, calcoliamo il area cuscinetto della piastra incorporata, che è l'area netta dopo aver sottratto l'area occupata dall'asta di ancoraggio.
Primo, Calcoliamo la dimensione massima di ancoraggio della testa efficace per la resistenza di estrazione, come da NEL 1992-4:2018 Clausola 7.2.1.5 Nota.
\(
d_{h,\testo{max}} = min sinistra( b_{\testo{incorporare _plate}}, 6 \sinistra( t_{\testo{incorporare _plate}} \giusto) + d_{\testo{anc}} \giusto)
= min sinistra( 60 \, \testo{mm}, 6 \volte (10 \, \testo{mm}) + 12 \, \testo{mm} \giusto)
= 60 \, \testo{mm}
\)
Successivamente, Calcoliamo l'area del cuscinetto netto della piastra incorporata circolare:
\(
UN_{brg} = frac{\pi}{4} \sinistra( \sinistra( d_{h,\testo{max}} \giusto)^ 2 – \sinistra( d_{\testo{anc}} \giusto)^2 a destra)
\)
\(
UN_{brg} = frac{\pi}{4} \volte sinistra( \sinistra( 60 \, \testo{mm} \giusto)^ 2 – \sinistra( 12 \, \testo{mm} \giusto)^2 a destra) = 2714.3 \, \testo{mm}^ 2
\)
Calcoliamo quindi il Design Resistenza di estrazione in cemento di ancoraggio in fusione in tensione usando NEL 1992-4:2018 Clausola 7.2.1.5:
\(
N_{Rd,S} = frac{k_2 a_{brg} f_{Eurocodice di design con piastra di base in acciaio}}{\Per calcolarlo{Mp}}
= frac{7.5 \volte 2714.3 \, \testo{mm}^2 \times 25 \, \testo{MPa}}{1.5}
= 339.29 \, \testo{kN}
\)
Ricorda il precedentemente calcolato carico di tensione per ancoraggio:
\(
N_{Ed} = frac{N_x}{N_{un carico,t}} = frac{50 \, \testo{kN}}{4} = 12.5 \, \testo{kN}
\)
Da 12.5 kN < 339.29 kN, La capacità di estrazione dell'ancora è sufficiente.
Dai un'occhiata #6: Calcola la capacità di scoppio della faccia laterale nella direzione Y
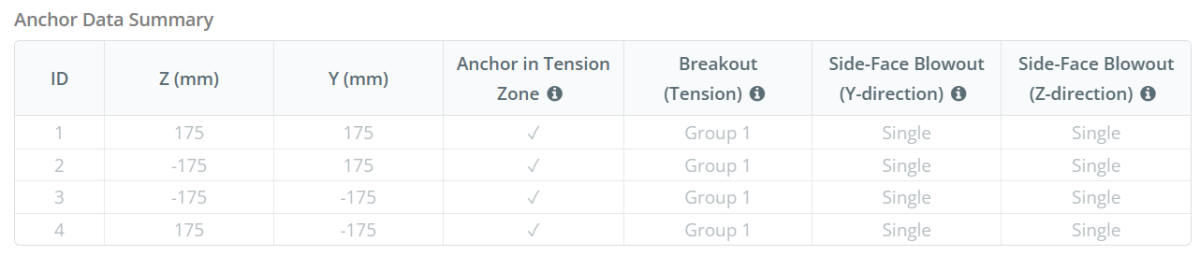
Consideriamo l'ID ancoraggio #3. Iniziamo calcolando la distanza del bordo per bordo di guasto.
\(
c_{z,\testo{min}} = min sinistra( c_{\testo{sinistra,Sforzo in alto Rinforzo}}, c_{\testo{giusto,Sforzo in alto Rinforzo}} \giusto)
= min sinistra( 75 \, \testo{mm}, 425 \, \testo{mm} \giusto)
= 75 \, \testo{mm}
\)
Successivamente, determiniamo la distanza del bordo per bordo ortogonale.
\(
c_{y,\testo{min}} = min sinistra( c_{\testo{superiore,Sforzo in alto Rinforzo}}, c_{\testo{parte inferiore,Sforzo in alto Rinforzo}} \giusto)
= min sinistra( 425 \, \testo{mm}, 75 \, \testo{mm} \giusto)
= 75 \, \testo{mm}
\)
Usando NEL 1992-4:2018 Eq. 7.27, Calcoliamo il Area proiettata di riferimento di un singolo dispositivo di fissaggio.
\(
A0_{c,N.B} = sinistra( 4 c_{z,\testo{min}} \giusto)^ 2
= sinistra( 4 \volte 75 \, \testo{mm} \giusto)^ 2
= 90000 \, \testo{mm}^ 2
\)
Dal momento che stiamo controllando la capacità del gruppo di ancoraggio, Prendiamo il area proiettata effettiva del gruppo di ancoraggio usando NEL 1992-4:2018 Eq. 7.27.
\(
UN_{Nc} = B_{c,N.B} Per calcolarlo{c,N.B} = 225 \, \testo{mm} \volte 200 \, \testo{mm} = 45000 \, \testo{mm}^ 2
\)
Dove,
\(
B_{c,N.B} = 2 c_{z,\testo{min}} + \min \left( 2 c_{z,\testo{min}}, c_{y,\testo{min}} \giusto)
= 2 \volte 75 \, \testo{mm} + \min \left( 2 \volte 75 \, \testo{mm}, 75 \, \testo{mm} \giusto)
= 225 \, \testo{mm}
\)
\(
Per calcolarlo{c,N.B} = 2 c_{z,\testo{min}} + \sinistra( \min \left( t_{\testo{conc}} – h_{\testo{ef}}, 2 c_{z,\testo{min}} \giusto) \giusto)
= 2 \volte 75 \, \testo{mm} + \sinistra( \min \left( 350 \, \testo{mm} – 300 \, \testo{mm}, 2 \volte 75 \, \testo{mm} \giusto) \giusto)
= 200 \, \testo{mm}
\)
Nel calcolo del Forza di esplosione concreta caratteristica di un'ancora individuale, noi useremo NEL 1992-4:2018 Eq. 7.26.
\(
N0_{controllare la capacità degli ancoraggi,cb} = k_5 a sinistra( \frac{c_{z,\testo{min}}}{\testo{mm}} \giusto)
\sinistra( \sqrt{\frac{UN_{\testo{brg}}}{\testo{mm}^ 2}} \giusto)
\sinistra( \sqrt{\frac{f_{Eurocodice di design con piastra di base in acciaio}}{\testo{MPa}}} \giusto) N
\)
\(
N0_{controllare la capacità degli ancoraggi,cb} = 8.7 \volte sinistra( \frac{75 \, \testo{mm}}{1 \, \testo{mm}} \giusto)
\volte sinistra( \sqrt{\frac{2714.3 \, \testo{mm}^ 2}{1 \, \testo{mm}^ 2}} \giusto)
\volte sinistra( \sqrt{\frac{25 \, \testo{MPa}}{1 \, \testo{MPa}}} \giusto)
\volte 0.001 \, \testo{kN}
\)
\(
N0_{controllare la capacità degli ancoraggi,cb} = 169.97 \, \testo{kN}
\)
Poi, otterremo il Parametri di scoppio della faccia laterale.
È possibile calcolare il parametro che tiene conto del disturbo della distribuzione delle sollecitazioni nel calcestruzzo NEL 1992-4:2018 Eq. 7.28.
\(
\Psi_{S,N.B} = min sinistra( 0.7 + 0.3 \sinistra( \frac{c_{y,\testo{min}}}{2 c_{z,\testo{min}}} \giusto), 1.0 \giusto)
= min sinistra( 0.7 + 0.3 \volte sinistra( \frac{75 \, \testo{mm}}{2 \volte 75 \, \testo{mm}} \giusto), 1 \giusto)
= 0.85
\)
Inoltre, I fattori per l'effetto di gruppo e il fattore L'influenza dell'eccentricità sono i seguenti:
\(
\Psi_{g,N.B} = 1
\)
\(
\Psi_{ec,N} = 1
\)
Infine, in riferimento a AS 5216:2021 Eq. 6.2.7 per aste di ancoraggio a testa, il progettare resistenza di esplosione in cemento è:
\(
N_{controllare la capacità degli ancoraggi,cb} = frac{N0_{controllare la capacità degli ancoraggi,cb} \sinistra( \frac{UN_{Nc}}{A0_{c,N.B}} \giusto) \sinistra( \Psi_{S,N.B} \giusto) \sinistra( \Psi_{g,N.B} \giusto) \sinistra( \Psi_{ec,N} \giusto)}{\Per calcolarlo{Mc}}
\)
\(
N_{controllare la capacità degli ancoraggi,cb} = frac{169.97 \, \testo{kN} \volte sinistra( \frac{45000 \, \testo{mm}^ 2}{90000 \, \testo{mm}^ 2} \giusto) \volte sinistra( 0.85 \giusto) \volte sinistra( 1 \giusto) \volte sinistra( 1 \giusto)}{1.5} = 48.159 \, \testo{kN}
\)
Richiamare carico di tensione per ancoraggio:
\(
N_{Ed} = frac{N_x}{N_{un carico,t}} = frac{50 \, \testo{kN}}{4} = 12.5 \, \testo{kN}
\)
Da 12.5 kN < 48.159 kN, Lo scoppio della faccia laterale in cemento lungo la direzione Y è sufficiente.
Qualsiasi altro numero ID di ancoraggio può essere utilizzato e produrrà lo stesso risultato, Poiché il design è simmetrico.
Dai un'occhiata #7: Calcola la capacità di scoppio della faccia laterale nella direzione z
La stessa procedura viene utilizzata nel calcolo della capacità di scoppio della faccia laterale nella direzione z. Consideriamo l'ID ancoraggio #2 questa volta. Ancora una volta, Iniziamo calcolando la distanza del bordo per bordo di guasto.
\(
c_{y,\testo{min}} = min sinistra( c_{\testo{superiore},Sforzo in alto Rinforzo}, c_{\testo{parte inferiore},Sforzo in alto Rinforzo} \giusto)
= min sinistra( 75 \, \testo{mm}, 425 \, \testo{mm} \giusto)
= 75 \, \testo{mm}
\)
Successivamente, determiniamo la distanza del bordo per bordo ortogonale.
\(
c_{z,\testo{min}} = min sinistra( c_{\testo{sinistra},Sforzo in alto Rinforzo}, c_{\testo{giusto},Sforzo in alto Rinforzo} \giusto)
= min sinistra( 75 \, \testo{mm}, 425 \, \testo{mm} \giusto)
= 75 \, \testo{mm}
\)
Usando NEL 1992-4:2018 Eq. 7.27, Calcoliamo il Area proiettata di riferimento di un singolo dispositivo di fissaggio.
\(
A0_{c,N.B} = sinistra( 4 c_{y,\testo{min}} \giusto)^ 2
= sinistra( 4 \volte 75 \, \testo{mm} \giusto)^ 2
= 90000 \, \testo{mm}^ 2
\)
Dal momento che stiamo controllando la capacità del gruppo di ancoraggio, Prendiamo il area proiettata effettiva del gruppo di ancoraggio usando NEL 1992-4:2018 Eq. 7.27.
\(
UN_{Nc} = B_{c,N.B} Per calcolarlo{c,N.B}
= 225 \, \testo{mm} \volte 200 \, \testo{mm}
= 45000 \, \testo{mm}^ 2
\)
Dove,
\(
B_{c,N.B} = 2 c_{y,\testo{min}} + \min \left( 2 c_{y,\testo{min}}, c_{z,\testo{min}} \giusto)
= 2 \volte 75 \, \testo{mm} + \min \left( 2 \volte 75 \, \testo{mm}, 75 \, \testo{mm} \giusto)
= 225 \, \testo{mm}
\)
\(
Per calcolarlo{c,N.B} = 2 c_{y,\testo{min}} + \sinistra( \min \left( t_{\testo{conc}} – h_{\testo{ef}}, 2 c_{y,\testo{min}} \giusto) \giusto)
= 2 \volte 75 \, \testo{mm} + \sinistra( \min \left( 350 \, \testo{mm} – 300 \, \testo{mm}, 2 \volte 75 \, \testo{mm} \giusto) \giusto)
= 200 \, \testo{mm}
\)
Nel calcolo del Forza di esplosione concreta caratteristica di un'ancora individuale, noi useremo NEL 1992-4:2018 Eq. 7.26.
\(
N0_{controllare la capacità degli ancoraggi,cb} = k_5 a sinistra( \frac{c_{y,\testo{min}}}{\testo{mm}} \giusto)
\sqrt{\sinistra( \frac{UN_{brg}}{\testo{mm}^ 2} \giusto)}
\sqrt{\sinistra( \frac{f_{Eurocodice di design con piastra di base in acciaio}}{\testo{MPa}} \giusto)} \, \testo{N}
\)
\(
N0_{controllare la capacità degli ancoraggi,cb} = 8.7 \sinistra( \frac{75 \, \testo{mm}}{1 \, \testo{mm}} \giusto)
\sqrt{\sinistra( \frac{2714.3 \, \testo{mm}^ 2}{1 \, \testo{mm}^ 2} \giusto)}
\sqrt{\sinistra( \frac{25 \, \testo{MPa}}{1 \, \testo{MPa}} \giusto)}
\Angolo di attrito 0.001 \, \testo{kN}
\)
\(
N0_{controllare la capacità degli ancoraggi,cb} = 169.97 \, \testo{kN}
\)
Poi, otterremo il Parametri di scoppio della faccia laterale.
È possibile calcolare il parametro che tiene conto del disturbo della distribuzione delle sollecitazioni nel calcestruzzo NEL 1992-4:2018 Eq. 7.28.
\(
\Psi_{S,N.B} = min sinistra( 0.7 + 0.3 \sinistra( \frac{c_{z,\testo{min}}}{2 c_{y,\testo{min}}} \giusto), 1.0 \giusto)
= min sinistra( 0.7 + 0.3 \volte sinistra( \frac{75 \, \testo{mm}}{2 \volte 75 \, \testo{mm}} \giusto), 1 \giusto)
= 0.85
\)
Inoltre, I fattori per l'effetto di gruppo e il fattore L'influenza dell'eccentricità sono i seguenti:
\(
\Psi_{g,N.B} = 1
\)
\(
\Psi_{ec,N} = 1
\)
Infine, in riferimento a AS 5216:2021 Eq. 6.2.7 per aste di ancoraggio a testa, il progettare resistenza di esplosione in cemento è:
Richiamare carico di tensione per ancoraggio:
\(
N_{Ed} = frac{N_x}{N_{un carico,t}} = frac{50 \, \testo{kN}}{4} = 12.5 \, \testo{kN}
\)
Da 12.5 kN < 48.159 kN, Lo scoppio della faccia laterale in cemento lungo la direzione Z è sufficiente.
Qualsiasi altro numero ID di ancoraggio può essere utilizzato e produrrà lo stesso risultato, Poiché il design è simmetrico.
Riepilogo del progetto
La Software di progettazione della piastra di base Skyciv Può generare automaticamente un rapporto di calcolo passo-passo per questo esempio di progettazione. Fornisce inoltre un riepilogo dei controlli eseguiti e dei loro rapporti risultanti, rendere le informazioni facili da capire a colpo d'occhio. Di seguito è riportata una tabella di riepilogo del campione, che è incluso nel rapporto.
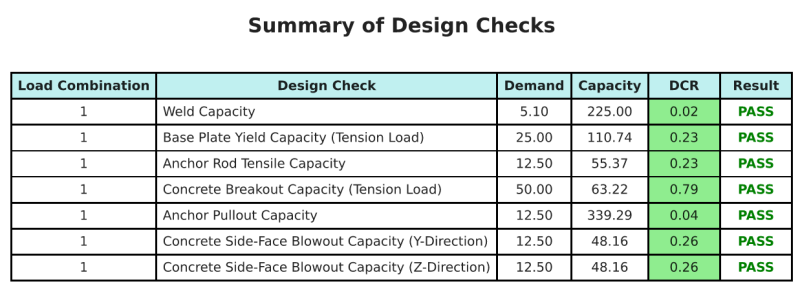
Rapporto campione Skyciv
Clicca qui Per scaricare un rapporto di esempio.
Acquista software di base
Acquista da solo la versione completa del modulo di progettazione della piastra di base senza altri moduli SkyCiv. Questo ti dà un set completo di risultati per la progettazione della piastra di base, tra cui report dettagliati e più funzionalità.
