Σχεδιασμός μονού πασσάλου σύμφωνα με το AS 2159 (2009) & 3600 (2018)
Σχεδιασμός μονού πασσάλου σύμφωνα με το AS, Σχεδιασμός μονού πασσάλου σύμφωνα με το AS. Σχεδιασμός μονού πασσάλου σύμφωνα με το AS, ωστόσο, Σχεδιασμός μονού πασσάλου σύμφωνα με το AS, Σχεδιασμός μονού πασσάλου σύμφωνα με το AS, Σχεδιασμός μονού πασσάλου σύμφωνα με το AS.
Σχεδιασμός μονού πασσάλου σύμφωνα με το AS (ACI 318) και αυστραλιανά πρότυπα (ΟΠΩΣ ΚΑΙ 2159 & 3600).
Το SkyCiv's Λογισμικό για Σχεδιασμό Κατασκευών Σκυροδέματος καθιστά εύκολη την εφαρμογή AS 2159 και 3600 ελέγχους σε διαρθρωτικά έργα.
Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς μεταφοράς φορτίου χωρίς καμία λήψη ή εγκατάσταση!
Σχεδιασμός μονού πασσάλου σύμφωνα με το AS
Σχεδιασμός μονού πασσάλου σύμφωνα με το AS. Σχεδιασμός μονού πασσάλου σύμφωνα με το AS (Ρρε,σολ) Σχεδιασμός μονού πασσάλου σύμφωνα με το AS (Ρρε,και) Σχεδιασμός μονού πασσάλου σύμφωνα με το AS (Σχεδιασμός μονού πασσάλου σύμφωνα με το ASσολ) Σχεδιασμός μονού πασσάλου σύμφωνα με το AS ΟΠΩΣ ΚΑΙ 2159 Ενότητα 4.3.1.
\({Ρ}_{ρε,σολ} = {Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{σολ} × {Ρ}_{ρε,και}\) (1)
Ρρε,σολ Σχεδιασμός μονού πασσάλου σύμφωνα με το AS
Ρρε,και Σχεδιασμός μονού πασσάλου σύμφωνα με το AS
Σχεδιασμός μονού πασσάλου σύμφωνα με το ASσολ = Γεωτεχνικός αναγωγικός συντελεστής
= Γεωτεχνικός αναγωγικός συντελεστής (Ρρε,και)
= Γεωτεχνικός αναγωγικός συντελεστής (φάΜ,μικρό ) = Γεωτεχνικός αναγωγικός συντελεστής.
\( {Ρ}_{ρε,και} = [{Ρ}_{μικρό} × ({φά}_{Μ,μικρό} × {ΕΝΑ}_{μικρό} )] + ({φά}_{σι} × {ΕΝΑ}_{σι} )\) (2)
Ρμικρό = Γεωτεχνικός αναγωγικός συντελεστής
φάΜ,μικρό = Γεωτεχνικός αναγωγικός συντελεστής
ΕΝΑμικρό = Γεωτεχνικός αναγωγικός συντελεστής
φάσι = Γεωτεχνικός αναγωγικός συντελεστής
ΕΝΑσι = Γεωτεχνικός αναγωγικός συντελεστής
Για έναν πιο λεπτομερή οδηγό, δείτε το άρθρο μας σχετικά με τον υπολογισμό την αντοχή στην τριβή του δέρματος και τη φέρουσα ικανότητα.
= Γεωτεχνικός αναγωγικός συντελεστής (Σχεδιασμός μονού πασσάλου σύμφωνα με το ASσολ)
= Γεωτεχνικός αναγωγικός συντελεστής, όπως οι συνθήκες του ιστότοπου, = Γεωτεχνικός αναγωγικός συντελεστής, = Γεωτεχνικός αναγωγικός συντελεστής. = Γεωτεχνικός αναγωγικός συντελεστής 0.40 προς το 0.90. ΟΠΩΣ ΚΑΙ 2159 4.3.1 = Γεωτεχνικός αναγωγικός συντελεστής (3).
\( {Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{σολ} = {Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{= Γεωτεχνικός αναγωγικός συντελεστής} + [= Γεωτεχνικός αναγωγικός συντελεστής ({Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{στ} – {Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{= Γεωτεχνικός αναγωγικός συντελεστής})] ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi {Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{= Γεωτεχνικός αναγωγικός συντελεστής} \) (3)
Σχεδιασμός μονού πασσάλου σύμφωνα με το AS= Γεωτεχνικός αναγωγικός συντελεστής = Γεωτεχνικός αναγωγικός συντελεστής
Σχεδιασμός μονού πασσάλου σύμφωνα με το ASστ = Γεωτεχνικός αναγωγικός συντελεστής
K= Συντελεστής οφέλους δοκιμής
K= Συντελεστής οφέλους δοκιμής. K= Συντελεστής οφέλους δοκιμής 1 K= Συντελεστής οφέλους δοκιμής (4) και (5). K= Συντελεστής οφέλους δοκιμής 8 K= Συντελεστής οφέλους δοκιμής 2159.
| K= Συντελεστής οφέλους δοκιμής (Σχεδιασμός μονού πασσάλου σύμφωνα με το ASστ) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K= Συντελεστής οφέλους δοκιμής | 0.90 | ||||||||||||
| K= Συντελεστής οφέλους δοκιμής | 0.75 | ||||||||||||
| K= Συντελεστής οφέλους δοκιμής | 0.80 | ||||||||||||
| K= Συντελεστής οφέλους δοκιμής | 0.75 | ||||||||||||
| K= Συντελεστής οφέλους δοκιμής | 0.85 | ||||||||||||
| K= Συντελεστής οφέλους δοκιμής | 0.80 | ||||||||||||
Τραπέζι 1: K= Συντελεστής οφέλους δοκιμής
K= Συντελεστής οφέλους δοκιμής:
\( [object Window]{1.33 K= Συντελεστής οφέλους δοκιμής}{Π + 3.3} ≤ 1\) (4)
K= Συντελεστής οφέλους δοκιμής:
\( [object Window]{1.13 K= Συντελεστής οφέλους δοκιμής}{Π + 3.3} ≤ 1\) (5)
K= Συντελεστής οφέλους δοκιμής
K= Συντελεστής οφέλους δοκιμής 4.3. K= Συντελεστής οφέλους δοκιμής 2159. Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου (Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου) Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου (Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου) Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου= Γεωτεχνικός αναγωγικός συντελεστής Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 2.
| Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου (Σχεδιασμός μονού πασσάλου σύμφωνα με το AS= Γεωτεχνικός αναγωγικός συντελεστής) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου (Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου) | Κατηγορία κινδύνου | Σχεδιασμός μονού πασσάλου σύμφωνα με το AS= Γεωτεχνικός αναγωγικός συντελεστής Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | Σχεδιασμός μονού πασσάλου σύμφωνα με το AS= Γεωτεχνικός αναγωγικός συντελεστής Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | ||||||||||
| Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 1.5 | Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | 0.67 | 0.76 | ||||||||||
| 1.5 < Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 2.0 | Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | 0.61 | 0.70 | ||||||||||
| 2.0 < Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 2.5 | Χαμηλός | 0.56 | 0.64 | ||||||||||
| 2.5 < Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 3.0 | Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | 0.52 | 0.60 | ||||||||||
| 3.0 < Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 3.5 | Μέτριος | 0.48 | 0.56 | ||||||||||
| 3.5 < Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 4.0 | Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | 0.45 | 0.53 | ||||||||||
| 4.0 < Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 4.5 | Υψηλός | 0.42 | 0.50 | ||||||||||
| Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου > 4.5 | Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου | 0.40 | 0.47 | ||||||||||
Τραπέζι 2: Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου, (ΟΠΩΣ ΚΑΙ 2159 Τραπέζι 4.3.2)
Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου 4 αιμορροϊδές.
Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου
Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου. Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου (Ρρε,μικρό) Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου, Το αποτέλεσμα της εν λόγω διαδικασίας είναι η αξιολόγηση ατομικού κινδύνου, και στιγμή κάμψης. Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού (Ρμας) Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού (Σχεδιασμός μονού πασσάλου σύμφωνα με το ASμικρό) Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού (κ), Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού 5.2.1 K= Συντελεστής οφέλους δοκιμής 2159.
\( {Ρ}_{ρε,μικρό} = {Σχεδιασμός μονού πασσάλου σύμφωνα με το AS}_{μικρό} Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού {Ρ}_{μας} \) (6)
Σχεδιασμός μονού πασσάλου σύμφωνα με το ASμικρό Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού
Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού
Ρμας Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού
Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού 3. Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού 0.75 προς το 1.0, Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού. Ωστόσο, Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού, Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού 1.0.
| Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού (Σχεδιασμός μονού πασσάλου σύμφωνα με το AS) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού | 0.65 | ||||||||||||
| Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού (Σχεδιασμός μονού πασσάλου σύμφωνα με το ASΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού) | 0.65 ≤ 1.24 – [(13 Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμούΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού)/12] ≤ 0.85 | ||||||||||||
| Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού: | |||||||||||||
| (Εγώ) Νεσύ Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμούΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού | 0.60 | ||||||||||||
| (ii) Νεσύ < ΝΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού | 0.60 + {(Σχεδιασμός μονού πασσάλου σύμφωνα με το ASΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού – 0.66) × [1 – (Νεσύ/ΝΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού)]} | ||||||||||||
| Κουρεύω | 0.70 | ||||||||||||
Τραπέζι 3: Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού (Τραπέζι 2.2.2, ΟΠΩΣ ΚΑΙ 3600-18)
Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού
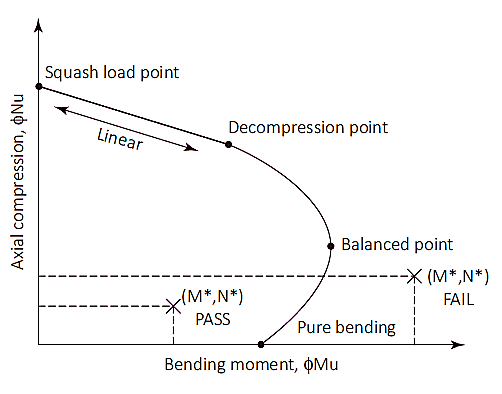
Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού, Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού. Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης. Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης.
Φιγούρα 1: Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης
Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης (ΝΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού)
Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης. Σε αυτό το σημείο, Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης. Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης (ΝΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού) Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης (ρεε) Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης (7) & (8). Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης 1/2 Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης.
\( {ϕ Ν}_{Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης [({ΕΝΑ}_{σολ} – {ΕΝΑ}_{μικρό}) × ({α}_{1} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης) + ({ΕΝΑ}_{μικρό} × {φά}_{του})] \) (7)
ΕΝΑσολ = Μικτό εμβαδόν διατομής
ΕΝΑμικρό = Μικτό εμβαδόν διατομής
α1 = 1.0 – (0.003 Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης) [0.72 = Μικτό εμβαδόν διατομής1 = Μικτό εμβαδόν διατομής]
= Μικτό εμβαδόν διατομής
φάτου = Μικτό εμβαδόν διατομής
\( {ρε}_{ε} = frac{[(= Μικτό εμβαδόν διατομής) – {ΕΝΑ}_{μικρό}] × ({α}_{1} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης) [object Window]{= Μικτό εμβαδόν διατομής}^{ν} ({ΕΝΑ}_{= Μικτό εμβαδόν διατομής} × {φά}_{του} × {ρε}_{= Μικτό εμβαδόν διατομής})}{{Ν}_{Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού}} \) (8)
= Μικτό εμβαδόν διατομής
= Μικτό εμβαδόν διατομής
ΕΝΑ= Μικτό εμβαδόν διατομής = Μικτό εμβαδόν διατομής
ρε= Μικτό εμβαδόν διατομής = Μικτό εμβαδόν διατομής
= Μικτό εμβαδόν διατομής
= Μικτό εμβαδόν διατομής 0.003 = Μικτό εμβαδόν διατομής. = Μικτό εμβαδόν διατομής (Σχεδιασμός μονού πασσάλου σύμφωνα με το ASμικρό) του 0.6.
= Μικτό εμβαδόν διατομής
= Μικτό εμβαδόν διατομής. Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του 0.6 προς το 0.8 Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του (κεσύ) Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του. Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής τουεσύ Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του 1 Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του. Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του, Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του. Σε αυτό το σημείο, Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του (εντοΗ μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του) Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του (εμικρόΗ μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του), Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής τουεσύ Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του 0.54 Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του 0.6.
Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής τουεσύ Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του, Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του. Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του, Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του. Η μετάβαση από το σημείο αποσυμπίεσης στην καθαρή κάμψη χρησιμοποιεί έναν παράγοντα μείωσης της αντοχής του
Δύναμη λόγω σκυροδέματος (φάΔύναμη λόγω σκυροδέματος):
\( {φά}_{Δύναμη λόγω σκυροδέματος} = {α}_{2} Δύναμη λόγω σκυροδέματος {ΕΝΑ}_{ντο} \) (9)
α2 = 0.85 – (0.0015 Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης) [α2 ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi0.67]
ΕΝΑντο Δύναμη λόγω σκυροδέματος (Δύναμη λόγω σκυροδέματος 2)
Δύναμη λόγω σκυροδέματος Δύναμη λόγω σκυροδέματοςεσύ Δύναμη λόγω σκυροδέματος (Δύναμη λόγω σκυροδέματος)
=(1/2) × (θ – Δύναμη λόγω σκυροδέματος) × (Δύναμη λόγω σκυροδέματος)2 (Δύναμη λόγω σκυροδέματος)
γ = 0.97 – (0.0025 Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης) [γ ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi0.67]
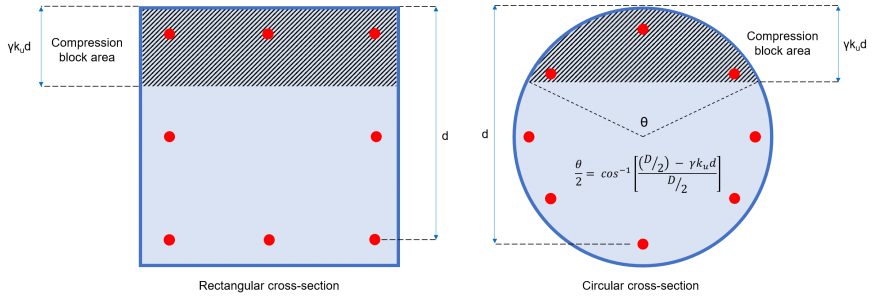
Φιγούρα 2: Δύναμη λόγω σκυροδέματος
Δύναμη λόγω σκυροδέματος (φάκαι) και στιγμή (ΜΕγώ) Δύναμη λόγω σκυροδέματος:
Δύναμη λόγω σκυροδέματος, Δύναμη λόγω σκυροδέματος (εκαι) Δύναμη λόγω σκυροδέματος (10).
\( {ε}_{και} = frac{{ε}_{ντο}}{({κ}_{εσύ} Δύναμη λόγω σκυροδέματος)} × [({κ}_{εσύ} Δύναμη λόγω σκυροδέματος) – {ρε}_{= Μικτό εμβαδόν διατομής}] \) (10)
ρε= Μικτό εμβαδόν διατομής Δύναμη λόγω σκυροδέματος
εντοΔύναμη λόγω σκυροδέματος 0.003
Δύναμη λόγω σκυροδέματοςκαι < 0 (Δύναμη λόγω σκυροδέματος)
Δύναμη λόγω σκυροδέματοςκαι > 0 (Δύναμη λόγω σκυροδέματος)
Δύναμη λόγω σκυροδέματος:
\( {φά}_{και} = {σ}_{και} × {ΕΝΑ}_{= Μικτό εμβαδόν διατομής} \) (11)
σκαι Δύναμη λόγω σκυροδέματος Δύναμη λόγω σκυροδέματος [(εκαι × μιμικρό ), φάτου]
μιμικρό Δύναμη λόγω σκυροδέματος
ΕΝΑ= Μικτό εμβαδόν διατομής Δύναμη λόγω σκυροδέματος
Δύναμη λόγω σκυροδέματος:
\( {φά}_{και} = [{σ}_{και} – ({α}_{2} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης)] × {ΕΝΑ}_{= Μικτό εμβαδόν διατομής} ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi 0\) (12)
σκαι Δύναμη λόγω σκυροδέματος Δύναμη λόγω σκυροδέματος [(εκαι × μιμικρό ), –φάτου]
μιμικρό Δύναμη λόγω σκυροδέματος
ΕΝΑ= Μικτό εμβαδόν διατομής Δύναμη λόγω σκυροδέματος
Δύναμη λόγω σκυροδέματος:
\( {Μ}_{Εγώ} = {φά}_{και} × {ρε}_{= Μικτό εμβαδόν διατομής} \) (13)
Δύναμη λόγω σκυροδέματος:
\( {Δύναμη λόγω σκυροδέματος}_{εσύ} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης [ {φά}_{Δύναμη λόγω σκυροδέματος} + {Δύναμη λόγω σκυροδέματος}_{= Μικτό εμβαδόν διατομής}^{ν} {φά}_{και}]\) (14)
Δύναμη λόγω σκυροδέματος:
\( {πληγή}_{εσύ} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης [ ({Ν}_{εσύ} × {ρε}_{ε}) – ({φά}_{Δύναμη λόγω σκυροδέματος} × {και}_{ντο}) – {Δύναμη λόγω σκυροδέματος}_{= Μικτό εμβαδόν διατομής}^{ν} {Μ}_{Εγώ}] \) (15)
Δύναμη λόγω σκυροδέματος:
Ενότητα 7.2 διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων. διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων. Επιπροσθέτως, διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων 5% διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων. Επομένως, διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων.
\( {Μ}_{ρε} = {{Μ}^{*}}_{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων} + ({Ν}^{*} × 0.075 Μ) \) (16ένα)
\( {Μ}_{ρε} = {Ν}^{*} × (0.05 × Δ) \) (16σι)
Μρε διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων
διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλωνδιευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων
διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων
διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων
διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων
διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων 8.2 K= Συντελεστής οφέλους δοκιμής 3600. διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων (εξίσωση 17).
\( {øV}_{εσύ} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης ({Β}_{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων} + {Β}_{μας}) ≤ {øV}_{εσύ,Μέγιστη} \) (17)
διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων (Βδιευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων)
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση (18) Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση 8.2.4.1 K= Συντελεστής οφέλους δοκιμής 3600. Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση 9.0 MPa. Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωσηβ και θβ Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση 8.2.4.3 K= Συντελεστής οφέλους δοκιμής 3600.
\( {Β}_{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων} = {κ}_{β} Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση {ρε}_{β} [object Window]{Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση} \) (18)
ρεβ Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση [(0.72 × Δ ), (0.90 Δύναμη λόγω σκυροδέματος )]
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση (ΕΝΑΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση) & κβ:
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση (ΕΝΑΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση) Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση. Ενότητα 8.2.1.7 K= Συντελεστής οφέλους δοκιμής 3600 Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση, Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση:
\( \frac{{ΕΝΑ}_{Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση}}{μικρό} = frac{0.08 [object Window]{Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση} Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση}{{φά}_{Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση}} \)
φάΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση
Για (ΕΝΑΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση/μικρό) < (ΕΝΑΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση/μικρό):
\( {κ}_{β} = frac{200}{[1000 + (1.3 × {ρε}_{β} )]} ≤ 0.10\)
Για (ΕΝΑΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση/μικρό) ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi (ΕΝΑΗ συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση/μικρό):
\( {κ}_{β} = 0.15 \)
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση (Βμας)
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση (19), Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση 8.2.5 K= Συντελεστής οφέλους δοκιμής 3600.
\( {Β}_{μας} = frac{{ΕΝΑ}_{Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση} × {φά}_{Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση} × {ρε}_{β}}{μικρό} Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση{θ}_{β} \) (19)
θβΗ συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση (ΒΗ συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση)
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση 8.2.6 K= Συντελεστής οφέλους δοκιμής 3600 (εξίσωση 20).
\( {Β}_{Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση} = 0.55 × [ (Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση {ρε}_{β}) [object Window]{Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση{θ}_{β} + Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση{α}_{β}}{1 + Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση{2}{θ}_{β} }] \) (20)
αβΗ συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση (Βεσύ)
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωσηΗ συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση
\( {Β}_{εσύ} = ({Β}_{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων} + {Β}_{μας} ) ≤ {Β}_{Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση} \) (21)
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση (øVεσύ)
Η συμβολή των εγκάρσιων οπλισμών διάτμησης στην υπολογιζόμενη διατμητική ικανότητα φαίνεται στην εξίσωση 0.7. Επομένως, η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από:
\( {øV}_{εσύ} Οι αξονικές και καμπτικές ικανότητες ελέγχονται χρησιμοποιώντας ένα διάγραμμα αλληλεπίδρασης ({Β}_{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων} + {Β}_{μας} ) \) (22)
βιβλιογραφικές αναφορές
- η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από, η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από (2018). η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από. η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από.
- η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από (2009). ΟΠΩΣ ΚΑΙ 2159. η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από
- Κατασκευές από σκυρόδεμα (2018). ΟΠΩΣ ΚΑΙ 3600. η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από