Το κέντρο ή το κέντρο μάζας των τμημάτων δοκού είναι χρήσιμο για ανάλυση δοκού όταν απαιτείται η ροπή αδράνειας για υπολογισμούς όπως η διάτμηση/καταπόνηση κάμψης και εκτροπή. Αυτό το άρθρο σας καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid και σας παρουσιάζει τον SkyCiv Free Centroid Calculator.
Αυτό το άρθρο σάς καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid
Αυτό το άρθρο σάς καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid, Αυτό το άρθρο σάς καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid. Τα τμήματα δοκού αποτελούνται συνήθως από ένα ή περισσότερα σχήματα. Έτσι, για να βρείτε το κεντροειδές μιας ολόκληρης περιοχής διατομής δοκού, πρώτα πρέπει να χωριστεί σε κατάλληλα τμήματα. Μετά από αυτό, η περιοχή και το κεντροειδές κάθε μεμονωμένου τμήματος πρέπει να ληφθούν υπόψη για να βρείτε το κεντροειδές ολόκληρης της ενότητας.
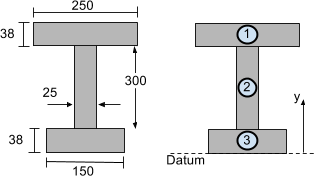
Εξετάστε την ενότητα I-beam που φαίνεται παρακάτω. Για τον υπολογισμό του κάθετου κεντροειδούς (στην κατεύθυνση y) μπορεί να χωριστεί σε 3 τμήματα όπως απεικονίζεται:
Now we simply need to use the centroid equation for finding the vertical (και) κεντροειδές σχήμα πολλών τμημάτων:
Θα πάρουμε το datum ή τη γραμμή αναφοράς από το κάτω μέρος του τμήματος δέσμης. Τώρα ας βρούμε ΑΕγώ και γΕγώ για κάθε τμήμα της ενότητας I-beam που φαίνεται παραπάνω, έτσι ώστε να μπορεί να βρεθεί το κατακόρυφο ή το y centroid.
[μαθηματικά]
\κείμενο{Τμήμα 1:}\\
\να αρχίσει{ευθυγραμμίζω}
{ΕΝΑ}_{1} &= 250 φορές38 = 9500 {\κείμενο{ χιλ}}^{2}\\
{και}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \κείμενο{ χιλ}\\\\
\τέλος{ευθυγραμμίζω}
[μαθηματικά]
[μαθηματικά]
\κείμενο{Τμήμα 2:}\\
\να αρχίσει{ευθυγραμμίζω}
{ΕΝΑ}_{2} &= 300 φορές25 = 7500 {\κείμενο{ χιλ}}^{2}\\
{και}_{2} &= 38 + \tfrac{300}{2} = 188 \κείμενο{ χιλ}\\\\
\τέλος{ευθυγραμμίζω}
[μαθηματικά]
[μαθηματικά]
\κείμενο{Τμήμα 3:}\\
\να αρχίσει{ευθυγραμμίζω}
{ΕΝΑ}_{3} &= 38 φορές 150 = 5700 {\κείμενο{ χιλ}}^{2}\\
{και}_{3} &= tfrac{38}{2} = 19 κείμενο{ χιλ}\\\\
\τέλος{ευθυγραμμίζω}
[μαθηματικά]
Σε περίπτωση που η διατομή αποτελείται από δύο υλικά ή ένα σύνθετο υλικό, τότε ένα από τα υλικά θα πρέπει να πολλαπλασιαστεί με τον αρθρωτό λόγο έτσι ώστε ολόκληρη η εξίσωση να γίνει ομοιόμορφη.
[μαθηματικά]
n = frac{ΜΙ_{1}}{ΜΙ_{2}}
[μαθηματικά]
Τυπικά, μι1 είναι ο συντελεστής ελαστικότητας του μη επικρατούμενου υλικού, και Ε2 είναι ο συντελεστής ελαστικότητας του επικρατούμενου υλικού, αν και όποια σειρά προτιμάται δεν θα επηρεάσει τη λύση του κεντροειδούς. Προσαρμογή για το δεύτερο υλικό, Αυτό το άρθρο σάς καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid.
[μαθηματικά]
\μπαρ{και}= frac{\άθροισμα{ΕΝΑ}_{Εγώ}{και}_{Εγώ}+\άθροισμα {ν}{ΕΝΑ}_{Εγώ}{και}_{Εγώ}}{\άθροισμα{ΕΝΑ}_{Εγώ}+\άθροισμα {ν}{ΕΝΑ}_{Εγώ}}
[μαθηματικά]
Find centroid of beam with SkyCiv
Finding centroid of beam is important but calculating them by hands can be time-consuming. Το SkyCiv προσφέρει ένα Αυτό το άρθρο σάς καθοδηγεί σε μια απλή διαδικασία υπολογισμού του centroid που αυτοματοποιεί αυτή τη διαδικασία για εσάς, βοηθώντας σας να βρείτε το κατακόρυφο (και) και οριζόντια (Χ) κεντροειδείς τομές δοκού εύκολα και με ακρίβεια!
Αυτό το εργαλείο είναι μια δωρεάν έκδοση του Οικοδόμος ενότητας SkyCiv, ένα ολοκληρωμένο διαδικτυακό λογισμικό ανάλυσης τμημάτων για την ανάλυση γεωμετρικών, κάμψη, ιδιότητες διάτμησης και στρέψης καθώς και σχεδιασμός FEA και οπλισμένου σκυροδέματος. Με αυτό το εργαλείο, μπορείτε να δημιουργήσετε προσαρμοσμένες ενότητες χρησιμοποιώντας προκαθορισμένα πρότυπα ή να ορίσετε τα δικά σας σχήματα με σημεία, γραμμές, ή εισαγωγές DXF από CAD.
Για να εξερευνήσετε όλη τη λειτουργικότητα Οικοδόμος ενότητας SkyCiv και βιώστε την ευκολία της μοντελοποίησης και της ανάλυσης του τμήματός σας, Εγγραφείτε δωρεάν σήμερα!
Σχετικοί πόροι
