Inhaltsverzeichnis
- Übersicht – Was ist das Trägheitsmoment
- Beispiel – Wie berechnet man das Trägheitsmoment
- Formel und Gleichungen
- Rechner
- Übungsfragen
Übersicht – Was ist das Trägheitsmoment?
Im Kontext des Bauingenieurwesens ist, das Trägheitsmoment eine Querschnittseigenschaft, die verwendet wird, um die Fähigkeit eines strukturellen Elements zu bestimmen, Biege- und Torsionskräften zu widerstehen. Es ist ein guter Indikator für die Steifigkeit und Festigkeit des Querschnitts unter Belastung. Ein höheres Trägheitsmoment bedeutet, dass die Struktur besser gegen Biegung und Durchbiegung gewappnet ist, was es zu einem entscheidenden Faktor bei der Gestaltung von Balken, Säulen, und anderen tragenden Bauteilen macht. Hinweis: Manchmal wird das Trägheitsmoment fälschlicherweise als zweites Trägheitsmoment, was jedoch nicht korrekt ist. Andere Bezeichnungen für das Trägheitsmoment sind: Flächenträgheitsmoment, oder zweites Flächenmoment.
Beispiel – Wie berechnet man das Trägheitsmoment eines Balkenquerschnitts
Bevor das Trägheitsmoment eines Balkenquerschnitts berechnet werden kann (auch als zweites Flächenmoment eines Balkenquerschnitts bezeichnet), muss sein Schwerpunkt (oder Massenmittelpunkt) bekannt sein. Zum Beispiel, wenn beispielsweise das Trägheitsmoment um die horizontale Achse (XX) benötigt wird, muss zunächst der vertikale Schwerpunkt (j) bestimmt werden (siehe dazu unsere Tutorials zur Berechnung des Schwerpunkts eines Balkens und des statischen/ersten Flächenmoments).
Bevor wir anfangen, wenn Sie nach unserem suchen kostenloser Trägheitsmomentrechner Bitte klicken Sie auf den Link, um mehr zu erfahren. Dadurch wird der Schwerpunkt berechnet, Trägheitsmoment, und andere Ergebnisse und zeigen Ihnen sogar die schrittweisen Berechnungen! Aber für den Moment, Schauen wir uns eine Schritt-für-Schritt-Anleitung und ein Beispiel für die Berechnung des Trägheitsmoments an:
Schritt 1: Segmentieren Sie den Balkenabschnitt in Teile
Bei der Berechnung des Flächenträgheitsmoments, Wir müssen das Trägheitsmoment kleinerer Segmente berechnen. Versuchen Sie, sie in einfache rechteckige Abschnitte zu unterteilen. Zum Beispiel, Betrachten Sie den folgenden Abschnitt des I-Trägers, was auch in unserem Zentroid-Tutorial vorgestellt wurde. Wir haben uns entschieden, diesen Abschnitt in zu unterteilen 3 rechteckige Segmente:
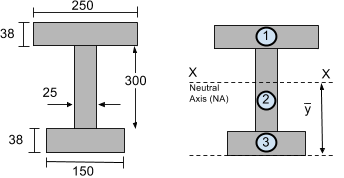
Schritt 2: Berechnen Sie die neutrale Achse (N / A)
Die neutrale Achse (N / A) oder die horizontale XX-Achse befindet sich am Schwerpunkt oder Massenschwerpunkt. In unserem Zentroid-Tutorial, Der Schwerpunkt dieses Abschnitts wurde zuvor gefunden 216.29 mm von der Unterseite des Querschnitts gefunden – Dies ist in unserem abgedeckt wie man den Schwerpunkt einer Form findet Lernprogramm. Auch diese lassen sich einfach aus unseren berechnen Schwerpunktrechner oder von gemein Schwerpunktgleichungen.
Schwerpunkt berechnen, oder neutrale Achse, ist wesentlich in Wie berechnet man das Trägheitsmoment eines Balkens?, da dies die Achse ist, auf der das Trägheitsmoment wirkt.
Schritt 3: Berechnen Sie das Trägheitsmoment
Um das Gesamtträgheitsmoment des Querschnitts zu berechnen, müssen wir das “Parallelachsentheorem”:

Da wir es in drei rechteckige Abschnitte unterteilt haben, müssen wir das Trägheitsmoment für jeden dieser Abschnitte berechnen. Es ist allgemein bekannt, dass die Trägheitsmomentgleichung eines Rechtecks um seine Schwerpunktachse einfach ist:
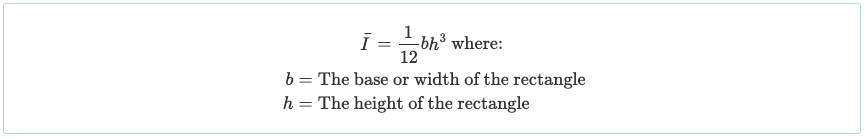
Das Trägheitsmoment anderer Formen wird häufig auf der Vorder- / Rückseite von Lehrbüchern oder in dieser Anleitung des Lehrbuchs angegeben Trägheitsmomentformen. Die rechteckige Form ist jedoch für Balkenabschnitte sehr häufig, es lohnt sich also wahrscheinlich auswendig zu lernen.
Jetzt haben wir alle Informationen, die wir brauchen, um mit dem “Parallelachsentheorem” das Gesamtträgheitsmoment des I-Trägerquerschnitts zu bestimmen. In unserem Beispiel:

Dort finden Sie unseren Leitfaden zur Berechnung der Momentfläche für Balkenabschnitte. Dieses Ergebnis ist im Hochbau von entscheidender Bedeutung und ein wichtiger Faktor für die Durchbiegung eines Trägers. Wir hoffen, dass Ihnen das Tutorial gefallen hat und freuen uns auf Ihre Kommentare. Für mehr Informationen, Besuchen Sie unser Tutorial auf Trägheitsmomentformel und Gleichungen.
Formel und Gleichungen
Jeder Abschnittstyp (rechteckig, Ich glänze, Kreisförmig) verfügt über eine eigene Formel zur schnellen Berechnung. Hierbei handelt es sich um vereinfachte Gleichungen, mit denen Ingenieure diese wichtige Eigenschaft schnell und einfach berechnen können.
Die Gleichungen sind ein vereinfachter Ausdruck der oben genannten Schritte. Ein Träger, Die Formel für das Trägheitsmoment eines Hohlrechtecks ist im Grunde das Trägheitsmoment des größeren Abschnitts – desto kleiner (intern) Sektion:

[Mathematik] \dfrac{bh^3}{12} – \dfrac{b_1h_1^3}{12} [Mathematik]
SkyCiv hat eine praktische Ressource für die Allgemeinheit zusammengestellt Formel für das Trägheitsmoment.
Rechner
Es gibt viele Möglichkeiten, das Trägheitsmoment zu berechnen, Eine davon ist die Verwendung von Software, um den Prozess zu vereinfachen.
SkyCiv Section Builder ist ein voll funktionsfähiges Profilentwurfstool, das weit über den Trägheitsmomentrechner hinausgeht. Außerdem erfahren Sie Schritt für Schritt, wie Sie das Trägheitsmoment ermitteln:
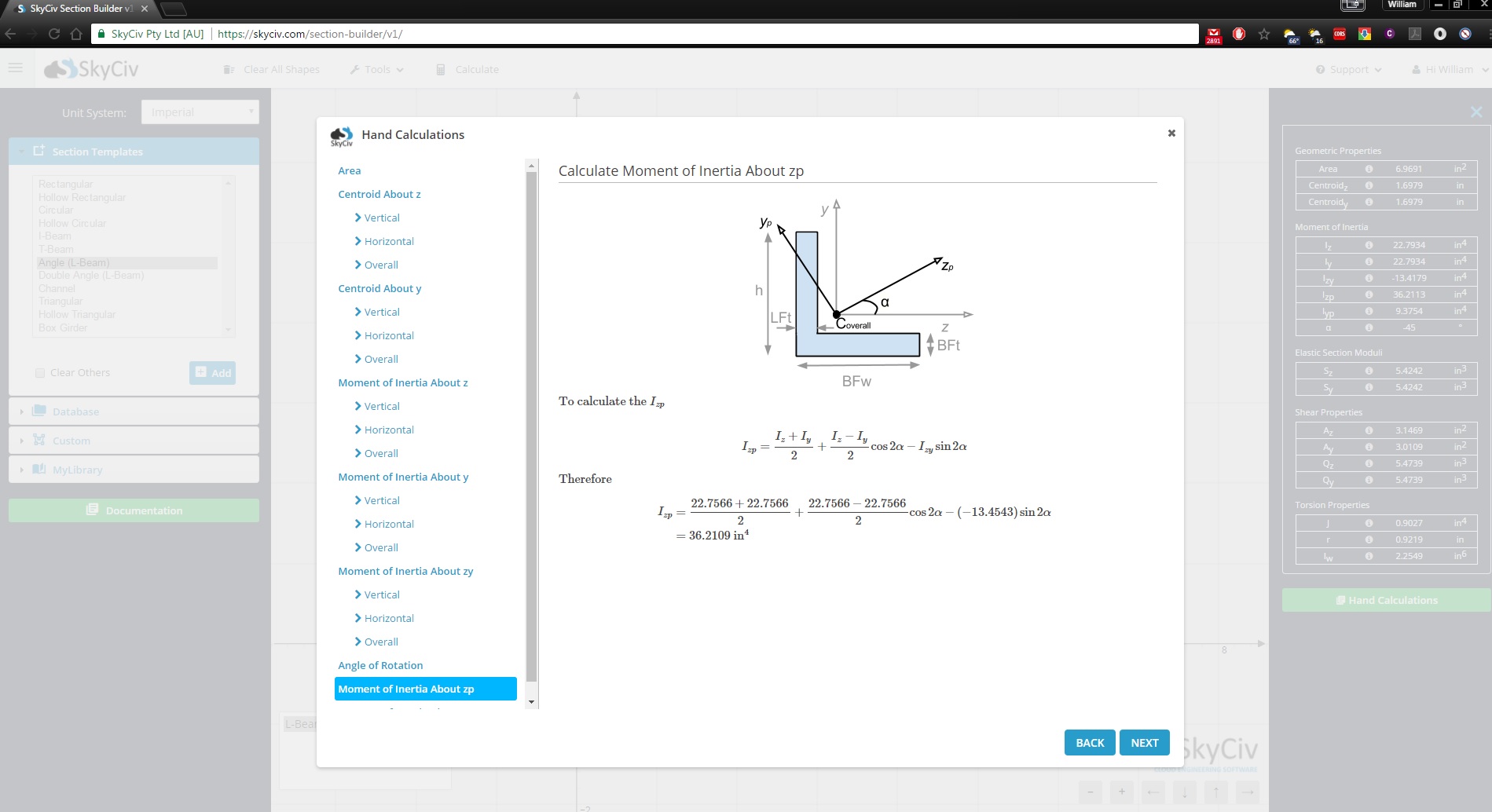
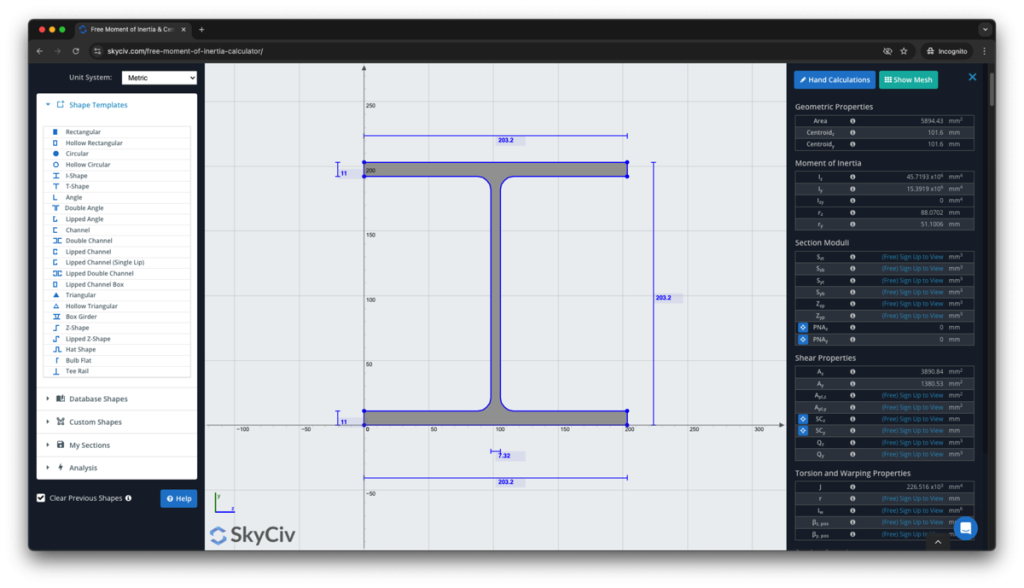
Melden Sie sich noch heute an, um mehr über die SkyCiv-Software zu erfahren, oder buchen Sie ein KOSTENLOSE DEMO um Unterstützung bei Ihren Engineering-Projekten für bestehende Benutzer zu erhalten!
zusätzlich, SkyCiv hat eine kostenlose Abschnittseigenschaftenrechner als Teil der Quick Design-Bibliothek. Es ist ein vereinfachtes Tool, berechnet aber auch das Trägheitsmoment gängiger Querschnittsformen.
Übungsfragen
Frage 1: Rechteckiger Abschnitt
Problem: Berechnen Sie das Trägheitsmoment (Ixx und Iyy) für einen rechteckigen Abschnitt mit einer Breite (b) von 200 mm und eine Höhe (h) von 300 mm.
Lösung: Die Formeln für das Trägheitsmoment eines Rechtecks lauten:
Ersetzen der angegebenen Werte:
- b=200 mm
- h=300 mm
Für Ixx:
Für Iyy:
Frage 2: Ich glänze
Problem: Berechnen Sie das Trägheitsmoment der Hauptachse (Ixx) eines I-Trägerabschnitts mit den folgenden Abmessungen:
- Breite des oberen Flansches (TFw) = 6 im
- Dicke des oberen Flansches (TFt) = 0.43 im
- Abschnittstiefe = 6 im
- Bahndicke (Wt) = 0.29 im
- Breite des unteren Flansches (BFw) = 6 im
- Dicke des unteren Flansches (BFt) = 0.43 im
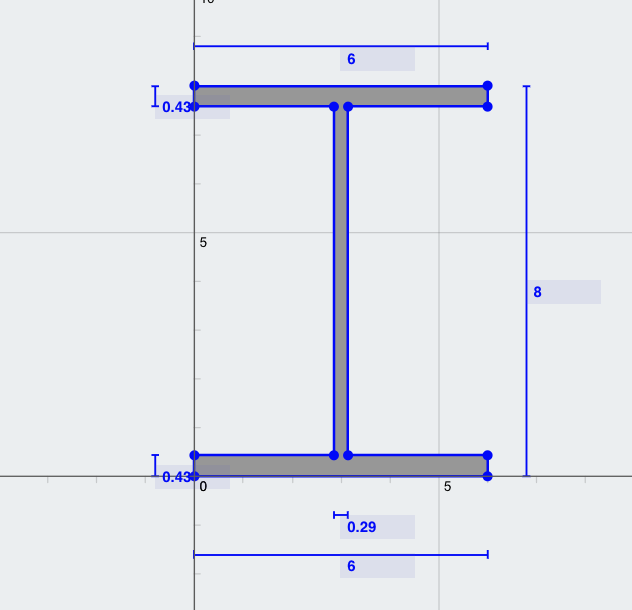
Lösung:


