Berechnung des seitlichen Erddrucks auf eine Stützmauer
Eine der Hauptlasten, die auf eine Stützmauer einwirken, ist der seitliche Erddruck. im Ruhezustand = k_, Eine gute Schätzung ihrer Größe und Verteilung ist entscheidend für die Gestaltung einer Stützmauer aus Beton. Im Allgemeinen, Abhängig von der Richtung, in die sich die Wand tendenziell bewegt, gibt es drei verschiedene Arten des seitlichen Erddrucks:
- Erdruhedruck: Wenn die Wand vollständig am Bewegen gehindert ist
- Aktiver Erddruck: Wenn die Wand vom zurückgehaltenen Boden wegkippen kann
- Passiver Erddruck: Wenn die Wand in den zurückgehaltenen Boden geschoben werden kann
In diesem Artikel, Wir werden uns auf die Beschreibung der Formeln für jeden der oben erwähnten Erddruckfälle konzentrieren.
Laterale Erddruckverteilung
Im Allgemeinen, Der laterale Erddruck verhält sich wie der hydrostatische Druck. Mit einem Nullwert an der Oberfläche und einem Maximalwert am tiefsten Punkt, der einer linearen Verteilung zwischen den beiden genannten Grenzen folgt. Deshalb, die horizontale Untergrundspannungsverteilung wird durch den folgenden Ausdruck beschrieben:
\(\sigma_h = K_* cdot (\Bereich z)\)
Wo \(K_*) nimmt den Wert von an \(K_o\) für den Fall des Ruhedrucks, \(K_a\) für den Fall des aktiven Drucks, sowie \(K_p\) für den Fall des passiven Drucks.
Integriert man den gegebenen Ausdruck für die seitliche Untergrundspannung aus \(0\) zu \(H\) im \([object Window]), das Ergebnis stellt sich heraus:
\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)
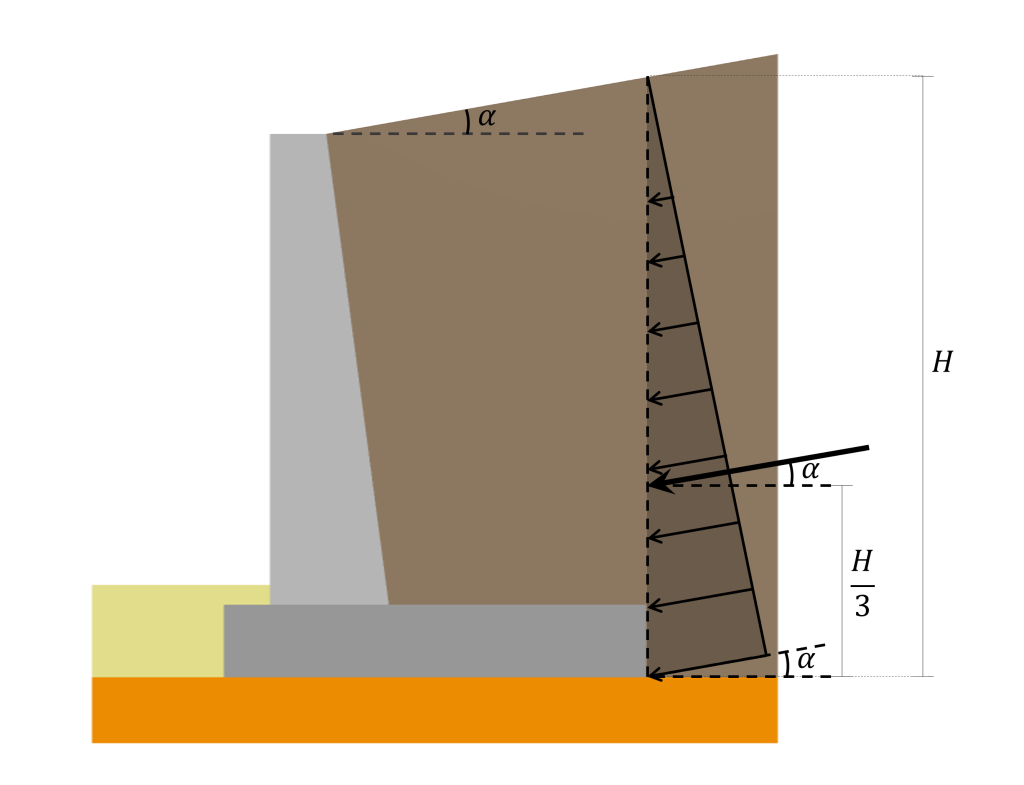
Die Wirkungslinie dieser Resultierenden ist lokalisiert \(\frac{2}{3}H\) von der Oberfläche. Die seitliche Erddruckverteilung, seine Resultante, und Lage wie oben beschrieben sind im folgenden Bild dargestellt:
Es ist wichtig zu erwähnen, dass die vorgestellte Verteilung und der resultierende Berechnungsansatz nur für Bodenpressungen gelten, die auf eine vertikale Rückseite wirken. Bei einer Stützmauer mit geneigter Rückseite (wie oben auf dem Bild), Die Oberfläche, auf der der Bodendruck wirkt, wird immer noch als vertikal betrachtet, da angenommen wird, dass er in einer vertikalen Ebene wirkt, die sich dort befindet, wo die Ferse endet.
zusätzlich, wenn die Verfüllung in einem gewissen Winkel geneigt ist \(\Alpha) in Bezug auf die Horizontale, die Druckverteilung und ihre Resultierende sind um denselben Winkel geneigt \(\Alpha) wie im Folgenden dargestellt:
Die korrekte Schätzung der seitlichen Erddruckverteilung und ihrer Resultierenden ist ein entscheidender Schritt im Stützmauer-Entwurfsprozess. Weitere Informationen darüber, wie dieser seitliche Erddruck in den Konstruktionsprozess für Stützmauern einbezogen wird, siehe Artikel Hier. Lassen Sie uns nun in die Formeln zur Berechnung des resultierenden seitlichen Erddrucks eintauchen, der vom Boden unter verschiedenen Bedingungen auf eine Stützmauer ausgeübt wird.
Seitlicher Erdruhedruck
Dieser Ansatz zur Berechnung des seitlichen Erddrucks gegen eine Stützmauer kann nur verwendet werden, wenn die Mauer vollständig in Ruhe ist und sich weder vom Boden weg noch in den Boden bewegen darf, diese Bedingung stellt sicher, dass die horizontale Dehnung im Boden Null ist. Für diesen Fall, der Koeffizient des Ruhedrucks (\(K_o\)) ist derjenige, der ersetzt \(K_*) in den vorherigen Gleichungen. Dieser Koeffizient ist die einzige Unbekannte zur Berechnung der Druckverteilung und ihrer Resultierenden. Für normal verfestigten Boden, die Beziehung für \(K_o\) ist:
\(K_o = 1-sünde(\Phi’)\)
Wo \(\phi’) ist der effektive Reibungswinkel des betrachteten Bodens.
Für überfestigte Böden, der Koeffizient kann unter Verwendung des folgenden Ausdrucks berechnet werden:
\(K_o = (1-ohne(\Phi’))\cdot OCR^{ohne(\Phi’)}\)
Wo \(\phi’) ist der effektive Reibungswinkel, sowie \(OCR\) das Überverfestigungsverhältnis des betrachteten Bodens.
Setzt man diesen Koeffizienten in den Ausdruck zur Berechnung der resultierenden Kraft aus dem seitlichen Erdruhedruck ein, so ergibt sich:
\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)
Aktiver seitlicher Erddruck
Der vorherige Ansatz kann verwendet werden, wenn die Wand überhaupt nicht nachgibt, jedoch, wenn sich eine Wand vom Boden wegbewegt, Der Bodendruck auf die Wand nimmt in jeder Tiefe ab. Für diesen Fall, der Koeffizient des aktiven Drucks (\(K_a\)) ist derjenige, der ersetzt \(K_*) in den Anfangsgleichungen. Verwenden von Rankines Ansatz für a körnige Verfüllung, und unter der Annahme, dass der Druck in a wirkt vertikale Rückseite, Der aktive Erddruckbeiwert kann mit der Gleichung berechnet werden:
\(K_a=cos(\Alpha) \frac{cos(\Alpha) – \sqrt{cos^2(\Alpha) – cos^2(\Phi’)}}{cos(\Alpha) + \sqrt{cos^2(\Alpha) – cos^2(\Phi’)}}\)
Wo \(\phi’) ist der Reibungswinkel des betrachteten Bodens und \(\Alpha) ist der Neigungswinkel der Verfüllfläche gegenüber der Horizontalen.
Setzt man diesen Koeffizienten in den Ausdruck zur Berechnung der resultierenden Kraft aus dem seitlichen Erddruck im aktiven Zustand ein, so ergibt sich:
\(P_a=frac{1}{2} \Gamma cdot H^2 cdot K_a)
Die zuvor vorgestellten Rankine-Wirkdruckberechnungen basieren auf der Annahme, dass die Wand reibungsfrei ist.
Passiver seitlicher Erddruck
Der auf eine Stützmauer wirkende seitliche Erddruck wird als passiv angesehen, wenn die Mauer in die Bodenmasse gedrückt wird, in diesem Zustand, die horizontale Spannung nimmt gegenüber dem Ruhezustand zu. Für diesen Fall, der Koeffizient des passiven Drucks (\(K_p\)) ist derjenige, der ersetzt \(K_*) in den Anfangsgleichungen. Verwenden von Rankines Ansatz für a körnige Verfüllung, und unter der Annahme, dass der Druck in a wirkt vertikale Rückseite, Der passive Erddruckbeiwert kann mit den Ausdrücken berechnet werden:
Wenn die Verfüllung vollständig horizontal ist
\(K_p = tan^2(45º+\frac{\Phi’}{2})\)
Wenn die Hinterfüllung um einen bestimmten Winkel gegenüber der Horizontalen geneigt ist
\(K_p=cos(\Alpha) \frac{cos(\Alpha) + \sqrt{cos^2(\Alpha) – cos^2(\Phi’)}}{cos(\Alpha) – \sqrt{cos^2(\Alpha) – cos^2(\Phi’)}}\)
Wo \(\phi’) ist der Reibungswinkel des betrachteten Bodens und \(\Alpha) ist der Neigungswinkel der Verfüllfläche gegenüber der Horizontalen.
Setzt man diesen Koeffizienten in den Ausdruck zur Berechnung der resultierenden Kraft aus dem seitlichen Erddruck im passiven Zustand ein, ergibt sich:
\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)
Nochmal, Die zuvor vorgestellten Rankine-Wirkdruckberechnungen basieren auf der Annahme, dass die Wand reibungsfrei ist.
Verweise
Stützmauer-Rechner
SkyCiv bietet einen kostenlosen Stützmauerrechner an, der den seitlichen Erddruck auf die Wand berechnet, und führen Sie eine Standsicherheitsanalyse Ihrer Stützmauern durch. Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des, Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des, wie man die Standsicherheit einer Stützmauer gegen Umkippen berechnet, Gleiten, und Lager!
Produkt Entwickler
BEng (Bürgerlich)