In Stahlverbindungsausführung, Schrauben sind normalerweise als eine Schraubengruppe konstruiert, die als ein Körper fungiert, um einer bestimmten Belastung standzuhalten. Die Festigkeit einer Schraubengruppe wird normalerweise anhand der steuernden Festigkeit ihrer kritischsten Schraube berechnet. Die direkten Lasten werden auf die Gesamtzahl der Schrauben verteilt, während das induzierte Moment aufgrund der Exzentrizität der Lasten in Bezug auf das Trägheitsmoment der Schraubengruppe und den Abstand vom Schwerpunkt verteilt wird. Diese Analyse wird als elastische Analyse bezeichnet. Aufgrund seiner vereinfachten und konservativen Annahmen zur Lastverteilung, es führt oft zu überdimensionierten Schraubverbindungen.
Wenn es um Value-Engineering und wirtschaftliche Designs geht, der unelastische Ansatz wird von den meisten Herstellern bevorzugt. Es erfordert eine geringere Anzahl von Schrauben für die gleiche Größenordnung von Lasten. Um den unelastischen Ansatz zu machen, das momentane Drehzentrum (ICOR) Methode mit Iterationen ist der beste Weg.
In diesem Artikel, Wir werden zeigen, wie man die Stärke von a berechnet Schraubverbindung mit der ICOR-Methode. Die Reaktionen pro Schraube werden mit Gleichung berechnet (7-1) auf Seiten 7-7 des AISC 15. Ausgabe Handbuch. Dies wird dann verwendet, um zu überprüfen, ob die angenommene Position des Momentanzentrums der Schraubengruppe korrekt ist. Schließlich, sobald wir den richtigen IC-Standort haben, Wir berechnen dann den Schraubengruppenkoeffizienten C, um seine Festigkeit zu bestimmen.
Die Verwendung der ICOR-Methode zum Ermitteln des Bolzengruppenkoeffizienten ist ein langwieriger Prozess, da eine Trial-and-Error-Methode zum Ermitteln des Momentanzentrums erforderlich ist (IC) Standort. Heutzutage, mit dem Einsatz von Computerlösern, Der IC einer Schraubengruppe kann einfach durch programmierte Iterationen berechnet werden. SkyCiv Bolt Group Solver verwendet eine schnelle Iterationsmethode, um die IC-Position und den Schraubengruppenkoeffizienten in nur wenigen Sekunden zu bestimmen. Es ist derzeit im AS implementiert 4100 Designcode, wird aber bald in die restlichen Designcodes integriert.
Abrufen der Schraubengruppeneigenschaften
Beginnen wir unsere einfache Analyse mit einer Schraubengruppe aus vier Schrauben, die mit einer exzentrischen vertikalen Querlast von belastet werden 10 Kips. Die Exzentrizität der Last entlang der x-Achse ist 4 Zoll rechts von der Schraubengruppe. Der Winkel von der Vertikalen ist null und die Exzentrizität entlang der y-Achse ist null.
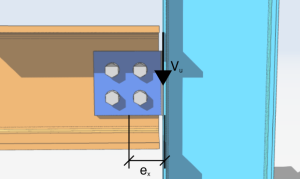
\(V_{u} = 10 Kips \)
\(\Theta = 0 Grad)
\(e_{x} = 4 in)
\(e_{und} = 0in)
Das erste, was Sie tun müssen, ist, die Koordinaten aller Schrauben in unserer Schraubengruppe zu erhalten. Die Verwendung von visuellen Leitfäden und Tabellen wird dringend empfohlen.
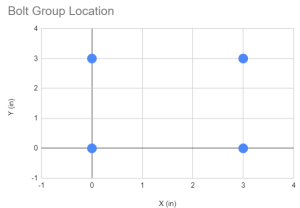
| Shop-ID | X. (im) | UND (im) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Um den Schwerpunkt der Schraubengruppe entlang des x zu erhalten- und y-Achsen, Wir brauchen die folgende Formel.
Lassen \(n \) = Gesamtzahl der Schrauben
\(X_{CG} = frac{\Summe X}{n}\)
\(Y_{CG} = frac{\Summe Y}{n} \)
Dann, Unsere Lösung ist:
\(X_{CG} = frac{\Summe X}{n} = frac{0 im + 0 im + 3 im + 3 im}{4} = 1.5 in)
\(Y_{CG} = frac{\Summe Y}{n} = frac{0 im + 3 im + 0 im + 3 im}{4} = 1.5 in)
Angenommen, der Standort des I.C.
Nachdem Sie den Schwerpunkt erhalten haben, wir nehmen den Ort des Augenblickszentrums an \(IC). Als erster Versuch, wir können davon ausgehen, dass sich der IC im geometrischen Schwerpunkt der Schraubengruppe befindet.
So, davon ausgehen
\(X_{IC} = X_{CG} = 1.5 in)
\(Y_{IC} = Y_{CG} = 1.5 in)
Dann, Wir tabellieren die Verschiebung jeder Schraube zur Position des IC. Wir können dies einfach tun, indem wir zuerst den Abstand entlang x und den Abstand entlang y ermitteln, dann erhalten Sie seine Verschiebung
| Shop-ID | cx (im) | cy (im) | c (im) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Wo,
\(c_{x} = X_{ich} – X_{IC}\)
\(c_{und} = Y_{ich} – Y_{IC}\)
\(c = sqrt{{\links(c_{x} \richtig)}^{2} + {\links(c_{und} \richtig)}^{2}}\)
Für Schraube Nr. 1, Unsere Lösung ist
\(c_{x} = 0 Zoll – 1.5 im = -1.5 in)
\(c_{und} = 0 Zoll – 1.5 im = -1.5 in)
\(c = sqrt{{\links( -1.5 in Recht)}^{2} + {\links( -1.5 in Recht)}^{2}} = 2.121in\)
Berechnen Sie die Verformung pro Schraube bzgl. Abstand von IC
Folglich, nachdem die Bolzenabstände von der angenommenen IC-Position erhalten wurden, Anschließend berechnen wir die Verformung jeder Schraube in Abhängigkeit von ihrem Abstand.
Die maximale Verformung pro Schraube, einstellen \(\Delta_{max} = 0.34 in), basiert auf experimentellen Daten für eine ASTM-Schraube, wie auf der AISC-Seite beschrieben 7-8. Durch die Verwendung eines linearen Anteils, und Einstellung \(\Delta_{max} = 0.34 in), Wir können die Verformung einer einzelnen Schraube relativ zu ihrem Anteil am maximalen Abstand berechnen \(c_{max}\). Die Gleichung für das Erhalten wird unten gezeigt.
\(\Delta_{1} = 0,34 Zoll times left( \frac{c}{c_{max}}\richtig) \)
Für Schraube Nr. 1, die Verformung ist
\(\Delta_{1} = 0,34 Zoll times left( \frac{2.121 im}{2.121 im}\richtig)\)
Für den Rest der Schrauben, die berechneten Verformungen sind unten tabelliert.
| Shop-ID | \(\Delta\) (im) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Holen Sie sich die Reaktionen pro Bolzen
Sobald wir die Verformung pro Schraube haben, wir können dann AISC 15th Ed verwenden. Gl (7-1) um die Reaktionen pro Schraube zu erhalten.
\(R = R_{ult} \links ( 1 – e^{-10\p-Delta-Effekte}\richtig )^{0.55}\)
Mit der \(R_{ult}\) in der Gleichung ist die angenommene Bruchlast einer Schraube, die wir als Schraubenscherfestigkeit einstellen können.
\(R_{ult} = φR_{n} \)
Für unser Beispiel, Wir verwenden eine Bolzenscherfestigkeit von \(24.4 pennen). Es ist auch zulässig, einen anderen Wert zu verwenden, da sich dieser bei der Berechnung des Schraubengruppenbeiwerts einfach aufhebt \(C) später.
Für Schraube Nr. 1, die berechnete Reaktion ist
\(R = R_{ult} \links ( 1 – e^{-10\p-Delta-Effekte}\richtig )^{0.55}\)
\(R = 24.4 kip links ( 1 – e^{-10 \mal links ( 0.34 in Recht )}\richtig )^{0.55}\)
\(R = 23.949 pennen)
Für den Rest der Schrauben, die berechneten Reaktionen sind wie folgt. Gleichzeitig, die Komponenten der Bolzenreaktion \(R) entlang x und y sind ebenfalls gezeigt.
| Shop-ID | R. (kip) | Rx (kip) | Ry (kip) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
Für Schraube Nr. 1, Die Lösungen zum Erhalten der x- und y-Komponenten sind unten gezeigt.
\(R_{x} = -R links ( \frac{c_{und}}{c} \richtig ) = -23.949 \mal links ( \frac{-1.5im}{2.121im} \richtig ) = 23.949 pennen)
\(R_{und} = R links ( \frac{c_{x}}{c} \richtig ) = 23.949 \mal links ( \frac{1.5im}{2.121im} \richtig ) = 23.949 pennen)
Außerdem, Wir sollten die induzierte Momentlast pro Schraube aufgrund der Exzentrizität erhalten. Um dies zu berechnen, Wir verwenden die Komponenten \(R_{x}\) sowie \(R_{und}\) und multipliziere sie mit den Exzentrizitäten \(c_{und}\) sowie \(c_{x}\), beziehungsweise.
Für Schraube Nr. 1, Momentan ist die Reaktion auf den IC
\(M_{r} = -R_{x}c_{und} + -R_{und}c_{x} \)
\(M_{r} = -16.937 kip times left ( -1.5in Recht) + -16.937 kip times left ( -1.5 in Recht ) \)
\(M_{r} = 50.811 Huhn-in)
Für den Rest der Schrauben, die entsprechenden Momentreaktionen sind unten tabelliert.
| Shop-ID | Herr (Hühnchen) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀Herr = 101.622 |
Überprüfung des IC-Standorts
Jetzt haben wir die Scher- und Momentreaktionen pro Schraube, Wir werden dies verwenden, um die Menge an Pu-Last zu bestimmen, der diese Schraubengruppe widersteht. Um dies zu tun, Wir erhalten die Resultierende der Summe aller Reaktionen entlang x und der Summe aller Reaktionen entlang y.
Aus dem vorherigen Abschnitt, das haben wir ausgerechnet
\(\Summe R_{x}=0 Huhn)
sowie
\(\Summe R_{und}=0 Huhn)
So,
\(P_{u} = Quadrat{{\links( \Summe R_{x} \richtig)}^{2} + {\links( \Summe R_{und} \richtig)}^{2}} = 0 pennen)
Da die resultierende Belastung \(P_{u} = 0kip), Wir können an dieser Stelle entscheiden, mit der Überprüfung nicht fortzufahren, da unsere Daten nur Null sind. Wir können auch schlussfolgern, dass der erste vermutete Standort von I.C., der sich im Schwerpunkt der Schraubengruppe befindet, ist falsch. jedoch, zum Zweck dieser Diskussion, Wir werden mit den folgenden Schritten fortfahren.
\(P_{ux} = -P_{u}Sündelinks ( \Theta richtig ) = 0 kip \)
\(P_{ui} = -P_{u}coslinks ( \Theta richtig ) = 0 kip \)
\(M_{u} = -P_{ux}\links ( Y_{CG} + e_{und} – Y_{IC} \richtig ) + -P_{ui} \links (X_{CG} + e_{x} – X_{IC} \richtig ) = 0 kip \)
Schon seit,
\(P_{ux} \neq sum R_{x} \)
\(P_{ui} \neq sum R_{und} \)
\(M_{u} \Ich bin nicht M_{r} \)
Deshalb, der vermutete Standort von I.C. ist falsch. Wir können jetzt mit dem nächsten angenommenen Ort fortfahren.
SkyCiv hat die Schraubengruppenberechnung vollständig in das australische Standardmodul integriert. Möchten Sie unsere Verbindungsdesign-Software ausprobieren?
Zweite Iteration
Für unsere zweite Iteration, Nehmen wir an, der I.C. befindet sich an den unten angegebenen Koordinaten.
Davon ausgehen
\(X_{IC} = 0.062 in)
\(Y_{IC} = 1.5 in)
Dann, Lassen Sie uns die Schritte ausführen, die wir in unserer ersten Iteration ausgeführt haben. Zusammenfassend, Die folgende Tabelle zeigt die Koordinaten, der Abstand jeder Schraube vom angenommenen I.C, und die entsprechende Verformung in Bezug auf den Abstand.
| Shop-ID | X. (im) | UND (im) | cx (im) | cy (im) | c (im) | \(\Delta\) (im) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Beachten Sie, dass der berechnete Schwerpunkt der Schraubengruppe immer noch derselbe ist, da sich an den Schraubenkoordinaten nichts geändert hat.
\(X_{CG} = 1.5 in)
\(Y_{CG} = 1.5 in)
Dann, wir berechnen die Reaktionen entlang x, Reaktionen entlang y, und dem entsprechenden Moment. Die Werte sind unten tabelliert.
| Shop-ID | R. (kip) | Rx (kip) | Ry (kip) | Herr (Hühnchen) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀Herr = 222 |
Als nächstes, wir bestimmen die resultierende Belastung aller Reaktionen entlang x und y.
\(P_{u} = Quadrat{{\links( \Summe R_{x} \richtig)}^{2} + {\links( \Summe R_{und} \richtig)}^{2}}\)
\(P_{u} = Quadrat{{\links( 0 kiprichtig)}^{2} + {\links( 40.703 kiprichtig)}^{2}}\)
\(P_{u} = 40.703 pennen)
Dann, die Komponenten der resultierenden Last basierend auf den gegebenen \(\theta\) wird unten gezeigt.
\(P_{ux} = -P_{u}Sünde links ( \Theta richtig ) = -41kip times sin left ( 0 Grad right )= 0 pennen)
\(P_{ui} = -P_{u}cos links ( \Theta richtig ) = -41kip times cos left ( 0 Grad right )= -41 pennen)
Wir werden diese Komponenten dann verwenden, um die Momentlast um den angenommenen I.C.
\(M_{u} = -P_{ux} \links ( Y_{CG} + e_{und} – Y_{IC} \richtig) + P_{ui} \links ( X_{CG} + e_{x} – X_{IC} \richtig)\)
\(M_{u} = -0 kip links ( 1.5 im +0 im – 1.5 in Recht) + 41 kip links ( 1.5 im +4 im – 0.06 in Recht)\)
\(M_{u} = -222 Huhn-in)
Als nächstes, vergleichen wir die errechneten P.ux, P.ux, sowie M.u zu den Reaktionen der Riegelgruppe.
\(P_{ux} \ca – \Summe R_{x}\)
\(P_{ui} \ca – \Summe R_{und}\)
\(M_{u} \ca – \Summe M_{u}\)
Da die linke Seite fast gleich der rechten Seite der Gleichung ist, wir können sagen, dass der angenommene Standort von I.C. ist richtig!
Auflösen nach dem C-Koeffizienten
Sobald der I.C. Standort bestimmt, Wir können jetzt den Schraubengruppenkoeffizienten C mit der folgenden Formel erhalten.
\(C = frac{P_{u}}{\Phi R_{n}} = \frac{40.703 kip}{24.4 kip} = 1.668\)
Kostenloser Schraubengruppenrechner
Prüfen Sie, wie wir unsere Schraubverbindungen mit diesem Ansatz konstruieren, indem Sie unsere verwenden Kostenloser Berechnungsrechner für Stahlverbindungen! Für mehr Funktionalität, Melden Sie sich noch heute für unsere Structural 3D-Software an, um loszulegen!

