Eine Anleitung zu den Berechnungen, die zum Entwerfen eines isolierten Fundaments erforderlich sind (IM 1992 & IM 1997)

Das Fundament ist ein wesentliches Bausystem, das Stützen- und Wandkräfte auf den tragenden Boden überträgt. Je nach Bodenbeschaffenheit und Gebäudelasten, Der Ingenieur kann wählen, ob er die Struktur auf einem flachen oder tiefen Fundamentsystem abstützen möchte³.

Die SkyCiv Foundation umfasst den Entwurf isolierter Fundamente gemäß Eurocode 2¹ und Eurocode 7².

Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Unser Tool ermöglicht es Benutzern, Foundation Design-Berechnungen ohne Download oder Installation durchzuführen!

Foundation Design Calculator

Entwurfsparameter eines isolierten Fundaments

Die in SkyCiv dargestellten Berechnungen verwenden die auf EN basierende präskriptive Methode 1997, Dabei wird ein angenommener sicherer Tragdruck zur Dimensionierung des Fundaments auf der Grundlage des Grenzzustands der Gebrauchstauglichkeit verwendet, gefolgt von der detaillierten Tragwerksplanung auf der Grundlage des Grenzzustands der Tragfähigkeit.

Abmessungsanforderungen

Zur Bestimmung der Abmessungen eines isolierten Fundaments, charakteristische Handlungen, wie Permanent/Tot (Q.), Variabel/Live (Ql), Wind (Qw), Seismisch (Qe), usw. werden für den Grenzzustand der Gebrauchstauglichkeit angewendet. Die kritische Belastungsanordnung/-kombination wird als Auslegungslast betrachtet, und wird mit dem zulässigen Bodendruck verglichen, wie in Gleichung . gezeigt 1. Dieses Beispiel beschränkt sich nur auf den gleichmäßigen Bodendruck.

\(\Text{q}_{\Text{ein}} = frac{\Text{P.}_{\Text{n}}}{\Text{Ein}} \rechter Pfeil \) Gleichung 1

wo:
q_ein = zulässiger Bodendruck
P._n = nicht berücksichtigte Bemessungslast
A = Fundamentfläche

Aus der Gleichung 1, q_ein sind im Austausch mit Ein.

\(\Text{Ein} = frac{\Text{P.}_{\Text{n}}}{\Text{q}_{\Text{ein}}} \rechter Pfeil \) Gleichung 1a

An dieser Stelle, Die Fundamentmaße können aus dem erforderlichen Flächenmaß zurückgerechnet werden, Ein.

Biegung

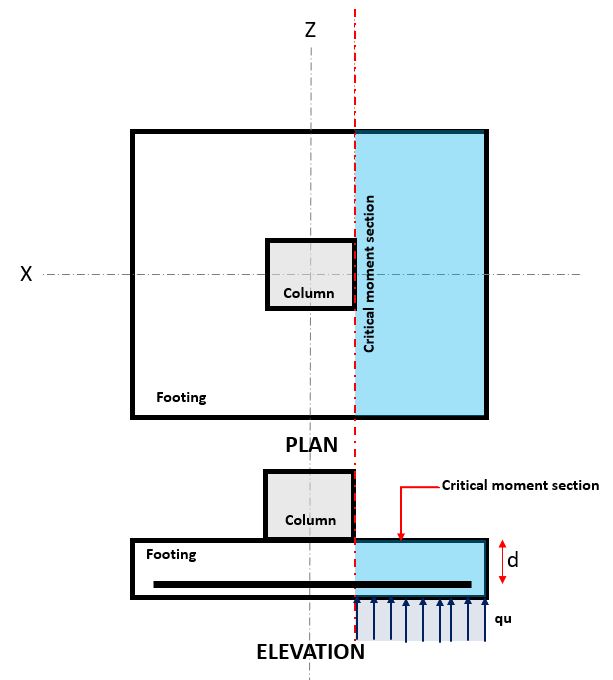
Abbildung 1. Kritischer Biegeabschnitt

Mit der Biege Grenzzustand tritt auf der kritische Biegeabschnitt, befindet sich an der Stirnseite der Stütze oben auf dem Fundament (Siehe Abbildung 1).

Mit der Biegebedarf, oder M._ED befindet sich in der Critical Flexure Section (blauer Lukenbereich) in Abbildung angegeben 1, und wird mit Gleichung . berechnet 2.

\( \Text{M.}_{u} = text{q}_{u} \mal links ( \frac{l_{x}}{2} – \frac{c_{x}}{2} \richtig ) \mal l_{mit} \mal links ( \frac{\frac{l_{x}}{2} – \frac{c_{x}}{2} }{2} \richtig ) \rechter Pfeil \) Gleichung 2

wo:
q_u = faktorisierter Bodendruck, kPa
l_x = Fundamentmaß entlang der x-Achse, mm
l_mit = Fundamentmaß entlang der z-Achse, mm
c_x = Spaltenabmessung entlang der x-Achse, mm

Mit der Biegekapazität, oder M.Kapazität wird mit Gleichung berechnet 3.

\(\Text{M.}_{Kapazität} = frac{1}{\Um es zu berechnen{S.,pt}} \mal f_{Ja} \mal A_{s} \mal links( d – \frac{s}{2} \richtig) \rechter Pfeil \) Gleichung 3

wo:
γ _S.,pt = Teilbeiwert für Betonstahl
l_x = Fundamentmaß parallel zur x-Achse, mm
l_mit = Fundamentmaß parallel zur z-Achse, mm
d = Abstand von der Extremdruckfaser zum Schwerpunkt der Längszugbewehrung, mm
Ein_s = Verstärkungsbereich, mm²
s = Tiefe des äquivalenten rechteckigen Spannungsblocks, mm
fyk = Verstärkungsstärke, MPa

Einwegschere

Mit der einachsige Scherung Grenzzustand, auch bekannt als Balkenscherung, liegt in einiger Entfernung “d” vom Gesicht einer Säule, an der kritischen Scherebene (Siehe Abbildung 2),

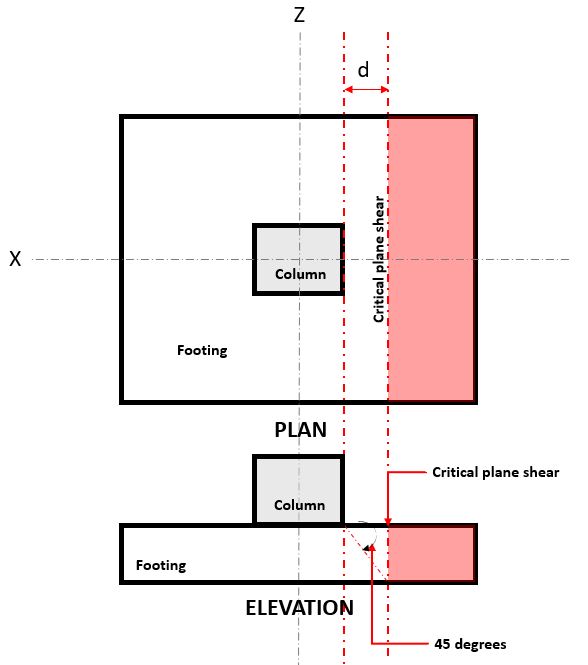
Abbildung 2. Kritische Ebenenschere der Einwegschere

Mit der Einweg Scheren Nachfrage oder V _ED wird unter der Annahme berechnet, dass das Fundament von der Stütze, in der sich die Fläche befindet, auskragt (rot) in Abbildung angegeben 2.

Mit der Einweg-Scherkapazität oder V _Rd,c ist definiert als die Scherfestigkeit im Grenzzustand der Tragfähigkeit (wenn keine Schubbewehrung erforderlich ist) und anhand der Gleichung berechnet 6 pro IM 1992, Sektion 6.2.2.

\(\Text{V }_{\Text{Rd,c}} = (\Text{C.}_{\Text{Rd,c}} \mal k times (100 \mal rho_{1} \mal text{f}_{\Text{ck}})^{\frac{1}{3}}) \mal text{b}_{\Text{w}} \mal text{d} \rechter Pfeil \) Gleichung 6 (IM 1992 Gl. 6.2.ein)

mit einem Minimum von

\(\Text{V }_{\Text{Rd,c}} = (0.035 \mal k^{\frac{3}{2}} \mal text{f}_{\Text{ck}}^{\frac{1}{2}}) \mal text{b}_{\Text{w}} \mal text{d} \rechter Pfeil \) Gleichung 9 (IM 1992 Gl. 6.2.b)

wo:
C._Rd,c = empfohlener Wert von 0,18/γ_C.
k = Koeffizient von 1 + √(200/d) ≤ 2.0
r₁ = A_sl / b_wd ≤ 0.02
f_ck = angegebene Betonfestigkeit, MPa
b_w = Breite des Fundaments, mm
d = Abstand von der Extremdruckfaser zum Schwerpunkt der Längszugbewehrung, mm

Der Scherbedarf und die Scherkapazität müssen überprüft werden, um den ultimativen Grenzzustand von EN zu erfüllen 1990:

\(\Text{E.}_{\Text{d}} \leq text{R.}_{\Text{d}} \rechter Pfeil \) Gleichung 4 (IM 1990 6.4.1)

SkyCiv-Stiftung, in Übereinstimmung mit Gleichung 4, berechnet das Einweg-Schereinheitsverhältnis (Gleichung 7) indem man den Scherbedarf über die Scherkapazität nimmt.

\( \Text{Einheitsverhältnis} = frac{\Text{Scherbedarf}}{\Text{Scherkapazität}} \rechter Pfeil \) Gleichung 7

Zwei-Wege-Schere

Mit der Zwei-Wege-Schere Grenzzustand, auch bekannt als Stanzschere, erweitert den kritischen Abschnitt auf eine Entfernung “2d” von der Stirnseite der Säule und um den Umfang der Säule. Die kritische Scherebene befindet sich in diesem Abschnitt des Fundaments (Siehe Abbildung 3).

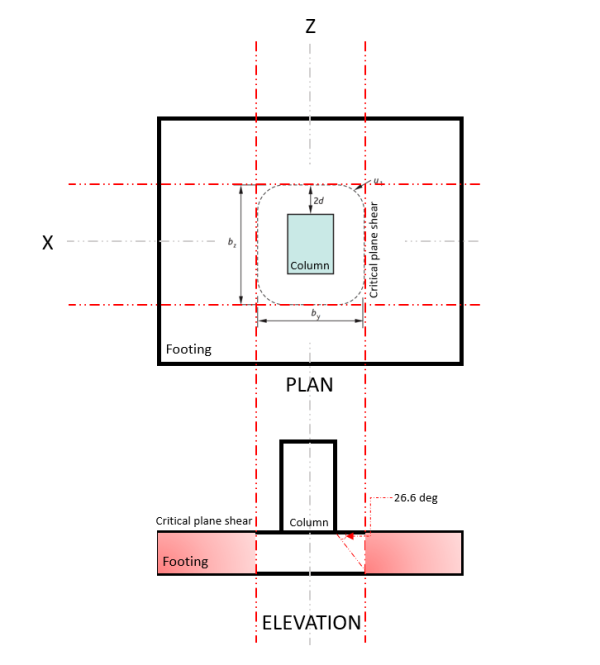
Abbildung 3. Kritische Scherebene der Zwei-Wege-Schere

Mit der Zwei WegeNachfrage hören oder V _ED tritt an der kritischen Scherebene auf, in Abbildung angegeben 3, in Übereinstimmung mit IM 1992, Sektion 6.4.2.

Mit der Scherkapazität oder V _Rd,c, ähnlich der Einweg-Scherkapazität (wenn keine Schubbewehrung erforderlich ist), wird auf Basis von EN berechnet 1992 Sektion 6.2.2 (Siehe Gleichung. 8).

\(\Text{V }_{\Text{Rd,c}} = (\Text{C.}_{\Text{Rd,c}} \mal k times (100 \mal rho_{1} \mal text{f}_{\Text{ck}})^{\frac{1}{3}}) \mal text{u}_{\Text{1}} \mal text{d} \rechter Pfeil \) Gleichung 8 (IM 1992 Gl. 6.2.ein)

mit einem Minimum von

\(\Text{V }_{\Text{Rd,c}} = (0.035 \mal k^{\frac{3}{2}} \mal text{f}_{\Text{ck}}^{\frac{1}{2}}) \mal text{u}_{\Text{1}} \mal text{d} \rechter Pfeil \) Gleichung 9 (IM 1992 Gl. 6.2.b)

 

wo:
u₁ = grundlegender Kontrollumfang, mm
Andere Variablen sind in ähnlicher Weise für die Einwegscherkapazität definiert.

Im Allgemeinen, Scherbedarf und Scherkapazität müssen der folgenden Gleichung entsprechen, um den ultimativen Grenzzustand von EN zu erreichen 1990:

\(\Text{E.}_{\Text{d}} \leq text{R.}_{\Text{d}} \rechter Pfeil \) Gleichung 4 (IM 1990 6.4.1)

SkyCiv-Stiftung, in Übereinstimmung mit der Gleichung 4, berechnet das Zwei-Wege-Schereinheitsverhältnis (Gleichung 10) indem man den Scherbedarf über die Scherkapazität nimmt.

\( \Text{Einheitsverhältnis} = frac{\Text{Scherbedarf}}{\Text{Scherkapazität}} \rechter Pfeil \) Gleichung 10

 

NEUE SkyCiv Foundation mit FEA

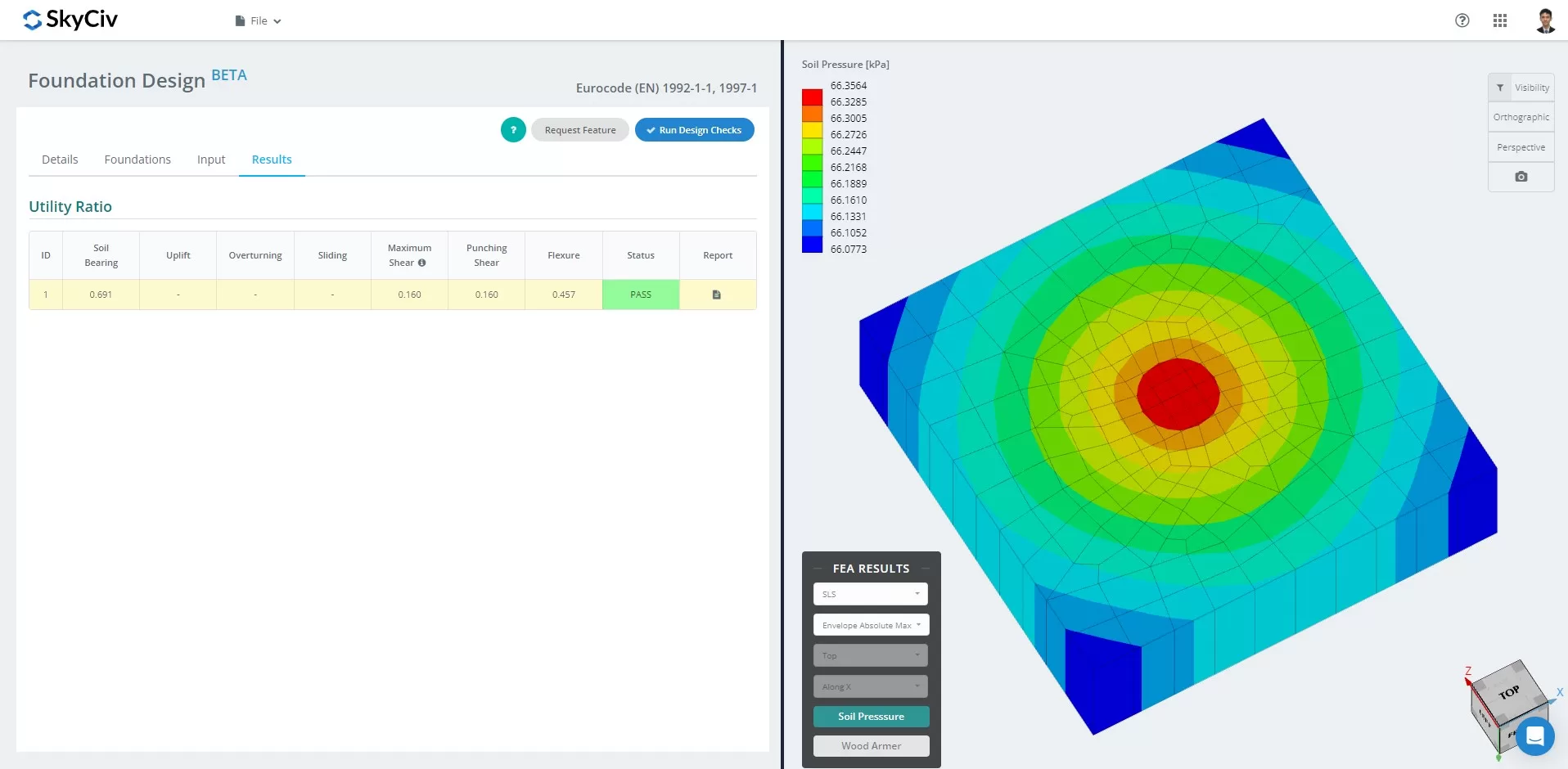
Stand März 2024, Das Foundation Design Module hat die Finite-Elemente-Analyse integriert (HÄSSLICH) Solver in seine Fähigkeiten. Mit dieser neuen Funktion können Benutzer detaillierte Bodendruck- und Holzarmierungsanalysen durchführen und gleichzeitig alle in der EN vorgeschriebenen Strukturprüfungen durchführen 1992 und 1997, einschließlich aller oben genannten Nachweise. Eine Zusammenfassung der FEA-Ergebnisse ist im umfassenden Bericht enthalten.

 

Kostenloser Betonfundamentrechner

Probieren Sie den kostenlosen Betonfundament-Rechner von SkyCiv aus, um Fundamente für Fundamente zu entwerfen, kombinierte Fußpunkte, Betonpfähle, Betonplatten, und vieles mehr.

Foundation Design Calculator