Ein voll funktionsfähiges Beispiel für Eurocode 1 (IM 1991-1-4) Windlastberechnungen
In diesem Beispiel, Wir berechnen den Auslegungswinddruck für eine Lagerstruktur in Aachen, Deutschland. Unsere Referenzen sind der Eurocode 1 IM 1991-1-4 Aktion auf Strukturen (Windlast) und DIN EN 1991-1-4 / NA:2010-12. Wir werden ein Modell aus unserem S3D verwenden, um zu demonstrieren, wie die Lasten auf jede Oberfläche aufgebracht werden.
Abbildung 1. Beispiel ein Lagermodell in SkyCiv S3D.
Abbildung 2. Standort (von Google Maps).
Tabelle 1. Gebäudedaten, die für unsere Windberechnung benötigt werden.
| Ort | Aachen, Deutschland |
|---|---|
| Belegung | Verschiedenes – Lagerstruktur |
| Terrain | Flaches Ackerland |
| Maße | 19.507 Mio. (d) × 31.699 Mio. (b) im Plan Traufhöhe von 9.144 m Scheitelhöhe in der Höhe. 10.973 Mio. (h) Dachneigung 3:16 (10.62°) Ohne zu öffnen |
| Verkleidung | Pfetten beabstandet bei 0.6 m Wandpfosten mit einem Abstand von 0.6 Mio. |
Die Formel zur Bestimmung des Auslegungswinddrucks lautet:
Für die Grundwindgeschwindigkeit:
\({v}_{b} = {c}_{dir} {c}_{Jahreszeit} {v}_{b,0}\) (1)
Wo:
\({v}_{b}\) = Grundwindgeschwindigkeit in m / s
\({c}_{dir}\) = Richtungsfaktor
\({c}_{Jahreszeit}\)= saisonaler Faktor
\({v}_{b,0}\) = Grundwert der Grundwindgeschwindigkeit (DIN Nationaler Anhang für EN 1991-1-4)
Für Grundgeschwindigkeitsdruck:
\({q}_{b} = 0.5 {⍴}_{Luft} {{v}_{b}}^{2} \) (2)
Wo:
\({q}_{b}\) = Auslegungswinddruck in Pa
\({⍴}_{Luft}\) = Luftdichte (1.25 kg / cu.m.)
\({v}_{b}\)= Grundwindgeschwindigkeit in m / s
Für Spitzendruck:
\({q}_{p}(mit) = 0.5 [1 + 7 {l}_{v}(mit)] {⍴}_{Luft} {{v}_{ Mio.}(mit)}^{2} \) (3)
Wo:
\({v}_{ Mio.}(mit)\) = mittlere Windgeschwindigkeit, m / s = \({c}_{r}(mit) {c}_{Das}(mit) {v}_{b}\) (4)
\({c}_{Das}(mit)\) = Topographiefaktor
\({c}_{r}(mit)\) = Rauheitsfaktor:
\({c}_{r}(mit) = {k}_{T.} ln(\frac{mit}{{mit}_{0}}) : {mit}_{Min.} ≤ {mit} ≤ {mit}_{max}\) (5)
\({c}_{r}(mit) = {c}_{r}({mit}_{Min.}) : {mit} ≤ {mit}_{Min.}\) (6)
Wo:
\({mit}_{0}\) = Rauhigkeitslänge, Mio.
\({k}_{T.}\) = Geländefaktor, abhängig von der Rauhigkeitslänge, \({mit}_{0}\) berechnet mit:
\({k}_{T.} = 0.19 {(\frac{{mit}_{0}}{{mit}_{0,II}})}^{0.07} \) : \( {mit}_{0,II} = 0.05\) (Geländekategorie II) (7)
\({mit}_{Min.}\) = Mindesthöhe
\({mit}_{max}\) = maximale Höhe angenommen als 200 Mio..
Aus diesen Gleichungen (4) zu (7), DIN EN 1991-1-4 / NA:2010-12 Anhang B fasst die Formel für jeden Parameter in Abhängigkeit von der Geländekategorie zusammen:
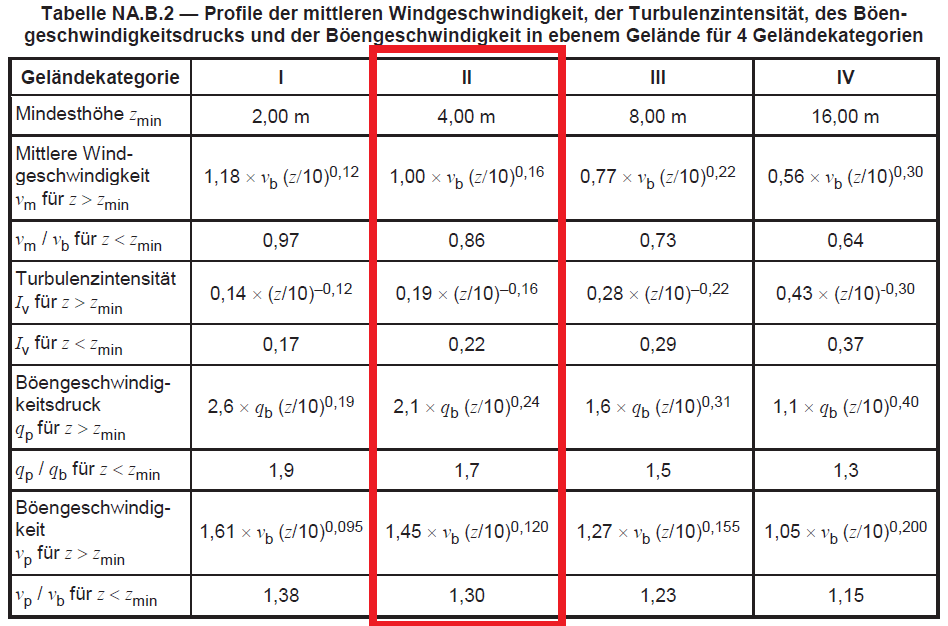
Abbildung 3. Tabelle NA.B.2 der DIN EN 1991-1-4 / NA:2010-12.
Jeder Parameter wird nachfolgend erläutert.
Geländekategorie
Die Struktur befindet sich auf Ackerland, welches klassifiziert ist als Geländekategorie II wie in Anhang A der EN definiert 1991-1-4 und Tabelle NA.B-1 des Nationalen Anhangs der DIN.
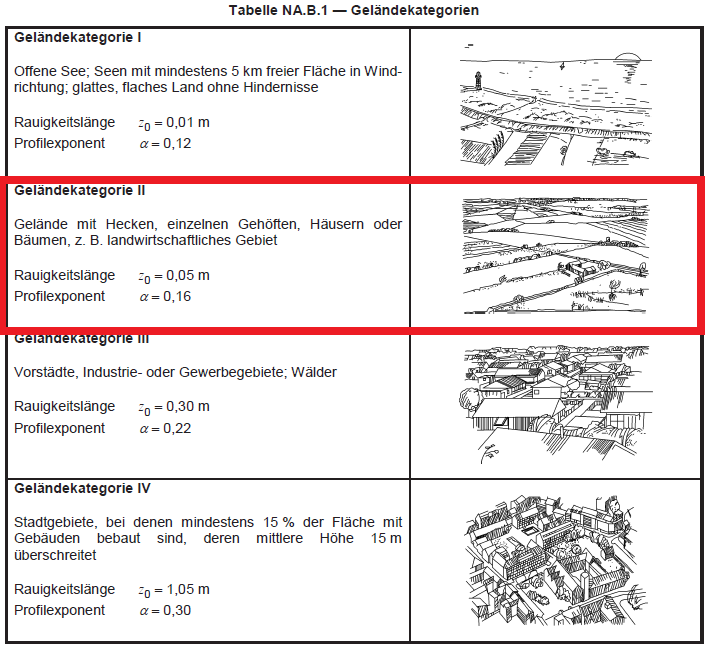
Abbildung 4. Tabelle NA.B.1 der DIN EN 1991-1-4 / NA:2010-12.
Richtungs- und Saisonfaktoren, \({c}_{dir}\) & \({c}_{Jahreszeit}\)
Um für Gleichung zu berechnen (1), Wir müssen die Richtungs- und Saisonfaktoren bestimmen, \({c}_{dir}\) & \({c}_{Jahreszeit}\). DIN Nationaler Anhang für EN 1991-1-4 vereinfacht diese Berechnung, da die vorgeschlagenen Werte dieser Faktoren gleich sind 1.0.
Grundlegende Windgeschwindigkeit und Druck, \({v}_{b,0}\) & \({q}_{b,0}\)
Wie bereits erwähnt, Die Windgeschwindigkeitskarte für Deutschland kann dem Nationalen Anhang der DIN für EN entnommen werden 1991-1-4. Jedes europäische Land verfügt über einen eigenen nationalen Anhang, in dem die vorgeschlagenen Windlastparameter von EN kalibriert werden 1991-1-4.
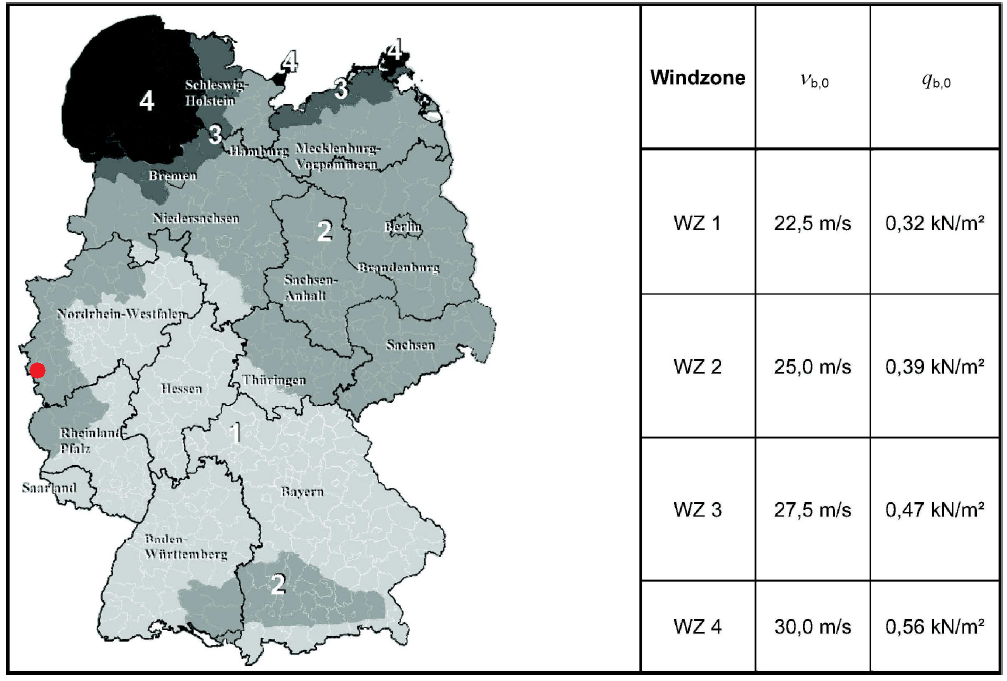
Abbildung 5. Tabelle NA.A.1 der DIN EN 1991-1-4 / NA:2010-12.
Für unseren Standort, Aachen, Deutschland liegt in WZ2 mit \({v}_{b,0}\) = 25.0 Frau wie in der obigen Abbildung gezeigt. Von diesem Wert, schon seit \({c}_{dir}\) & \({c}_{Jahreszeit}\) sind beide gleich 1.0, Wir können den Grundwinddruck berechnen, \({q}_{b,0}\), unter Verwendung von Gleichungen (1) und (2). Daher, der entsprechende Wert von \({q}_{b,0}\) = 0.39 kPa, auch in der Windkarte des Nationalen Anhangs der DIN für EN angegeben 1991-1-4.
SkyCiv automatisiert jetzt die Erkennung von Windregionen und das Abrufen des entsprechenden Windgeschwindigkeitswerts mit nur wenigen Eingaben. Versuchen unsere SkyCiv Free Wind Tool
Mittlere Windgeschwindigkeit, \({v}_{ Mio.}(mit)\)
Um den Spitzendruck zu berechnen, \({q}_{p}(mit)\), Wir müssen den Wert der mittleren Windgeschwindigkeit bestimmen, \({v}_{ Mio.}(mit) \). Aus der Abbildung 3, wir können die mittlere Geschwindigkeit berechnen, \({v}_{ Mio.}(mit) \):
Zum \({mit}_{Min.} ≤ {mit} ≤ {mit}_{max} : 1.0 {v}_{b} {(0.1mit)}^{0.16} \)
Zum \({mit}_{Min.} ≤ {mit} ≤ {mit}_{max} : 0.86 {v}_{b} \)
Spitzendruck, \({q}_{p}(mit)\)
Ähnlich, der Spitzendruck, \({q}_{p}(mit)\), kann mit Abbildung gelöst werden 3:
Zum \({mit}_{Min.} ≤ {mit} ≤ {mit}_{max} : 2.1 {q}_{b} {(0.1mit)}^{0.24} \)
Zum \({mit} ≤ {mit}_{Min.} : 1.7 {q}_{b} \)
Um den Spitzendruck zu berechnen, \({q}_{p}(mit) \), Wir müssen den Wert der mittleren Windgeschwindigkeit bestimmen, \({v}_{ Mio.}(mit) \). Aus der Abbildung 3, wir können die mittlere Geschwindigkeit berechnen, \({v}_{ Mio.}(mit) \):
für \({mit}_{Min.} ≤ {mit} ≤ {mit}_{max} : 1.0 {v}_{b} {(0.1mit)}^{0.16} \)
für \({mit} ≤ {mit}_{Min.} : 0.86 {v}_{b} \)
Die Ergebnisse für die mittlere Windgeschwindigkeit und den Spitzendruck für jedes Niveau sind in der Tabelle gezeigt 2 unten.
Tabelle 2. Berechnete mittlere Windgeschwindigkeit und Spitzendruck für jede Ebene der Struktur.
| Höhe / Ebene | \({v}_{ Mio.}(mit)\), Frau | \({q}_{p}(mit)\), Gut |
|---|---|---|
| 3.00 | 21.5 | 664.06 |
| 6.00 | 23.04 | 725.66 |
| 9.00 | 24.58 | 799.83 |
| 10.97 (h) | 25.37 | 838.80 |
Externer Winddruck, \({w}_{e}\)
Bei Berechnung des Spitzendrucks, \({q}_{p}(mit)\), Der auf die Oberfläche der Struktur wirkende äußere Winddruck kann mit gelöst werden:
\({w}_{e} = {q}_{p}(mit) {c}_{auf}\) (8)
Wo:
\({w}_{e}\) = externer Winddruck, Gut
\({q}_{p}(mit)\) = Spitzendruck, Gut
\({c}_{auf}\) = Druckkoeffizient für die Außenfläche
ein) Vertikale Wände
Zur Verteilung des Winddrucks (Zone D.), Sektion 7.2.2 oder und 1991-1-4 beschreibt, wie es je nach verteilt werden soll \(h ), \(b\), und \(d\). Für unser Beispiel, wir haben \(h < b\) (10.973 < 31.699 Mio.), daher, \({mit}_{e} = h\) wie in Abbildung gezeigt 6.
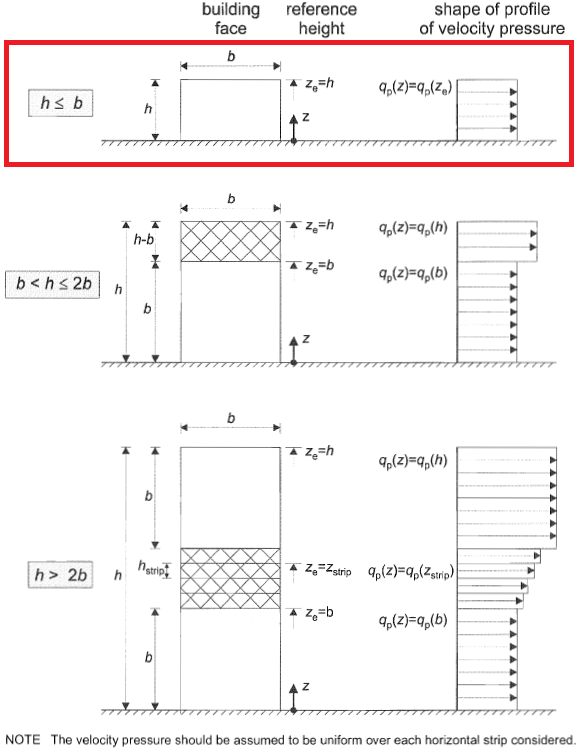
Abbildung 6. Druckverteilung für die Luvwand basierend auf Abbildung 7.4 oder und 1991-1-4.
Andererseits, Druckverteilung für Seitenwände (Zonen A bis C.) sind in Abbildung dargestellt 7.5 oder und 1991-1-4 und hängt von der \(e = b < 2h ). Für unser Beispiel, der Wert von \(e = 21.946\), daher, \(e > d\) wie in Abbildung gezeigt 7. Außerdem, Der Lee-Wanddruck wird als Zone E bezeichnet. Externe Druckkoeffizienten sind dann in Abbildung angegeben 8 basierend auf Tabelle NA.1 der DIN EN 1991-1-4 / NA:2010-12.
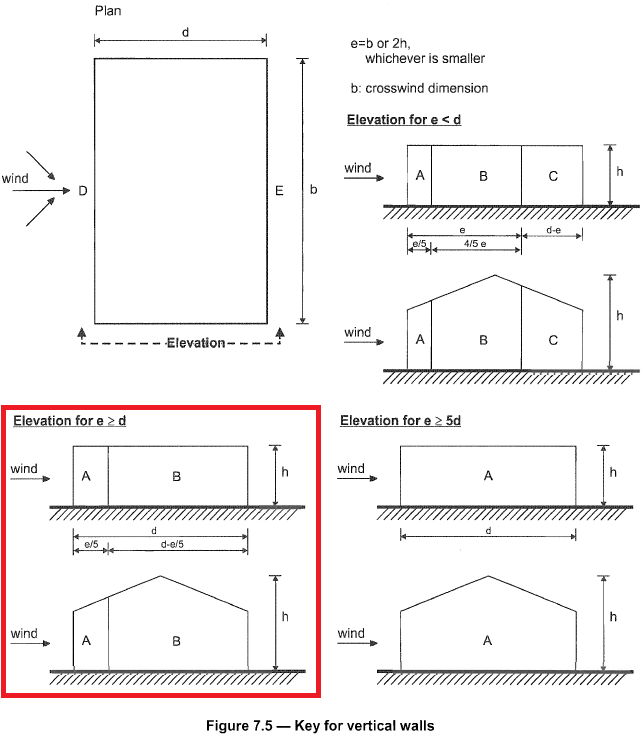
Abbildung 7. Druckverteilung für Seitenwand basierend auf Abbildung 7.5 oder und 1991-1-4.
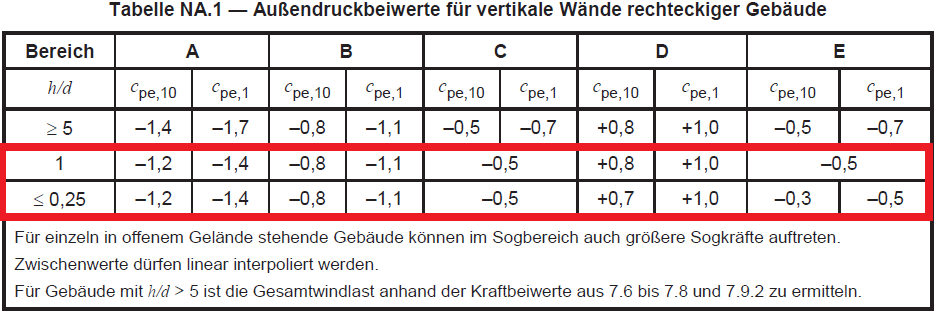
Abbildung 8. Außendruckkoeffizient für vertikale Wände (Zonen A bis E.) basierend auf Tabelle NA.1 der DIN EN 1991-1-4 / NA:2010-12.
Schon seit \(h / d = 0.563\), wir müssen das interpolieren \({c}_{auf}\) Werte zur Berechnung des Auslegungswinddrucks. Die Indizes für \({c}_{auf,10}\) und \({c}_{auf,1}\) bedeutet, dass der Wert von dem Bereich abhängt, in dem der Winddruck angewendet wird, für entweder 1 qm. und 10 qm. Üblicherweise, für Gebäude, \({c}_{auf,10}\) ist derjenige, der seitdem angenommen werden soll \({c}_{auf,1}\) wird für kleine Elemente wie Verkleidungen und Dachelemente verwendet. Die interpolierten Werte für \({c}_{auf}\) sind in der Tabelle gezeigt 3 unten.
Tabelle 3. Berechneter Außendruckkoeffizient für vertikale Wände.
| \(h / d ) | Ein | B. | C. | D. | E. |
|---|---|---|---|---|---|
| 1.000 | -1.2 | -0.8 | -0.5 | 0.8 | -0.5 |
| 0.563 | -1.2 | -0.8 | -0.5 | 0.742 | -0.383 |
| 0.250 | -1.2 | -0.8 | -0.5 | 0.7 | -0.3 |
b) Dach
Die Verteilung der Auslegungswinddrücke für das Dach ist in den Abschnitten beschrieben 7.2.3 zu 7.2.10 und 7.3 oder und 1991-1-4. Speziell, da das Dachprofil unserer Struktur Duopitch ist, Wir werden Section verwenden 7.2.5 um die Dachaußendruckkoeffizienten zu erhalten, \({c}_{auf}\), wie in Abbildung gezeigt 9 und 10 unten.
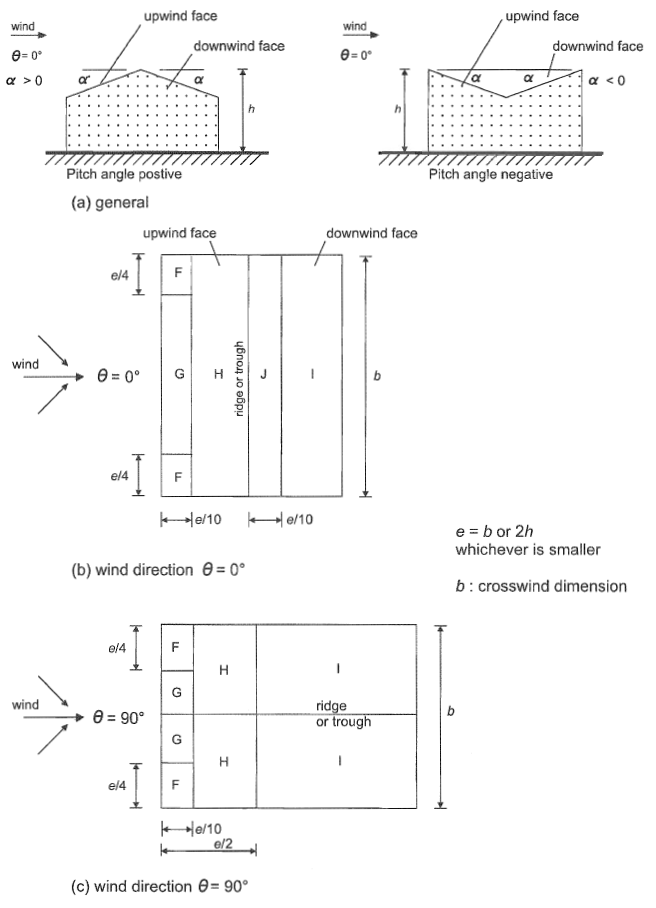
Abbildung 9. Druckverteilung für Duopitchdach basierend auf Abbildung 7.8 oder und 1991-1-4.
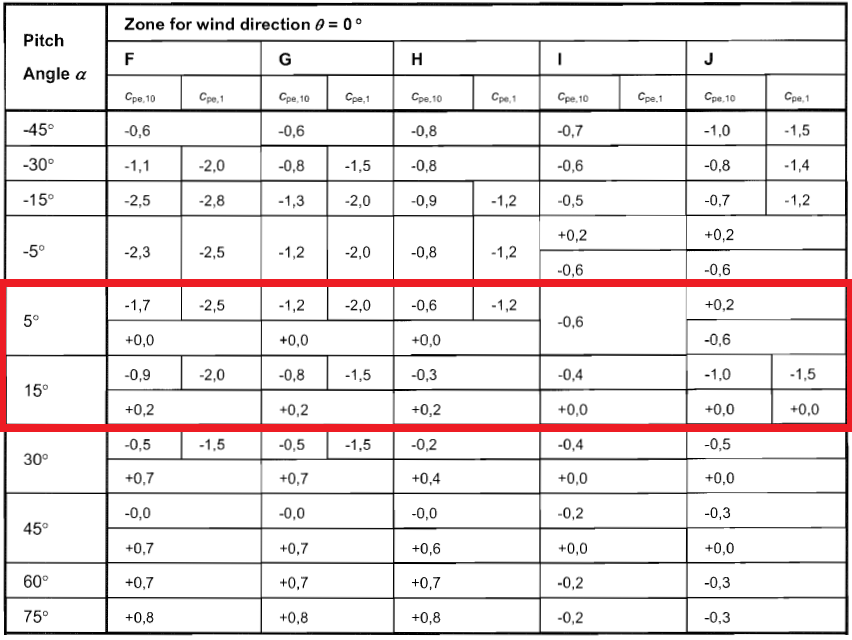
Abbildung 9. Außendruckkoeffizient für Dachflächenwände (Zonen F bis J.) basierend auf Tabelle 7.4a von EN 1991-1-4.
Da der Dachneigungswinkel gleich 10,62 ° ist, wir müssen das interpolieren \({c}_{auf}\) Werte von 5 ° und 15 °. Daher, das berechnete \({c}_{auf}\) Die Werte für unsere Struktur sind in der Tabelle aufgeführt 4 unten.
Tabelle 4. Berechneter Außendruckkoeffizient für Dachflächen.
| \(h / d ) | Zone F. | Zone G. | Zone H. | Zone I. | Zone J. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(-{c}_{bleibt die}\) | \(+{c}_{bleibt die}\) | \(-{c}_{bleibt die}\) | \(+{c}_{bleibt die}\) | \(-{c}_{bleibt die}\) | \(+{c}_{bleibt die}\) | \(-{c}_{bleibt die}\) | \(+{c}_{bleibt die}\) | \(-{c}_{bleibt die}\) | \(+{c}_{bleibt die}\) | |
| 5.00 | -1.7 | 0.0 | -1.2 | 0.0 | -0.6 | 0.0 | -0.6 | – | -0.6 | 0.2 |
| 10.62 | -1.250 | 0.112 | -0.975 | 0.112 | -0.431 | 0.112 | -0.488 | – | -0.825 | 0.088 |
| 15.00 | -0.9 | 0.2 | -0.8 | 0.2 | -0.3 | 0.2 | -0.4 | – | -1.0 | 0.0 |
Interner Winddruck, \({w}_{ich}\)
Interner Winddruck, \({w}_{ich}\), kann sich entwickeln und wirkt gleichzeitig mit dem äußeren Winddruck. Daher, die Notwendigkeit zu berechnen \({w}_{ich}\) ist notwendig. Die zu berechnende Formel \({w}_{ich}\) ist:
\({w}_{ich} = {q}_{p}(mit) {c}_{Pi}\) (9)
Wo:
\({w}_{ich}\) = innerer Winddruck, Gut
\({q}_{p}(mit)\) = Spitzendruck, Gut
\({c}_{Pi}\) = Innendruckkoeffizient
Sektion 7.2.9 oder und 1991-1-4 besagt, dass \({c}_{Pi}\) kann als die lästigere von genommen werden +0.2 und -0.3. Wir gehen davon aus, dass unsere Struktur keine dominante Öffnung hat.
Winddruck auslegen
Mit diesen \({c}_{auf}\) und \({c}_{Pi}\) Werte, Wir können nun den entsprechenden externen Winddruck für jede Zone berechnen, wie in der Tabelle gezeigt 5.
Tabelle 5. Berechneter externer Winddruck für jede Oberfläche.
| Oberfläche | Zone | \({w}_{e}\) | \({w}_{ich}\) | Kombiniert \({w}_{e}\) und \({w}_{ich}\) | |||
|---|---|---|---|---|---|---|---|
| \(-{c}_{auf}\) | \(+{c}_{auf}\) | \(+{c}_{Pi}\) | \(+{c}_{Pi}\) | min Wert | Maximalwert | ||
| Mauer | Zone A. | -1006.56 | 167.76 | -251.64 | -1174.32 | 754.92 | |
| Zone B. | -671.04 | – | -838.80 | -419.40 | |||
| Zone C. | -419.40 | – | -587.16 | 167.76 | |||
| Zone D. | – | 622.11 | 454.35 | 873.75 | |||
| Zone E. | -321.54 | – | -489.30 | -69.9 | |||
| Dach | Zone F. | -1048.83 | 94.28 | -1216.59 | 345.92 | ||
| Zone G. | -818.00 | 94.28 | -985.76 | 345.92 | |||
| Zone H. | -361.86 | 94.28 | -529.62 | 345.92 | |||
| Zone I. | -409.00 | -576.76 | -157.36 | ||||
| Zone J. | -691.84 | 73.48 | -859.60 | 325.12 | |||
Aus diesen Werten, Wir können diese Konstruktionswinddrücke jetzt auf unsere Struktur anwenden. Betrachtet man einen Rahmenschacht (innere), das kombinierte \({w}_{e}\) und \({w}_{ich}\) ist wie folgt:
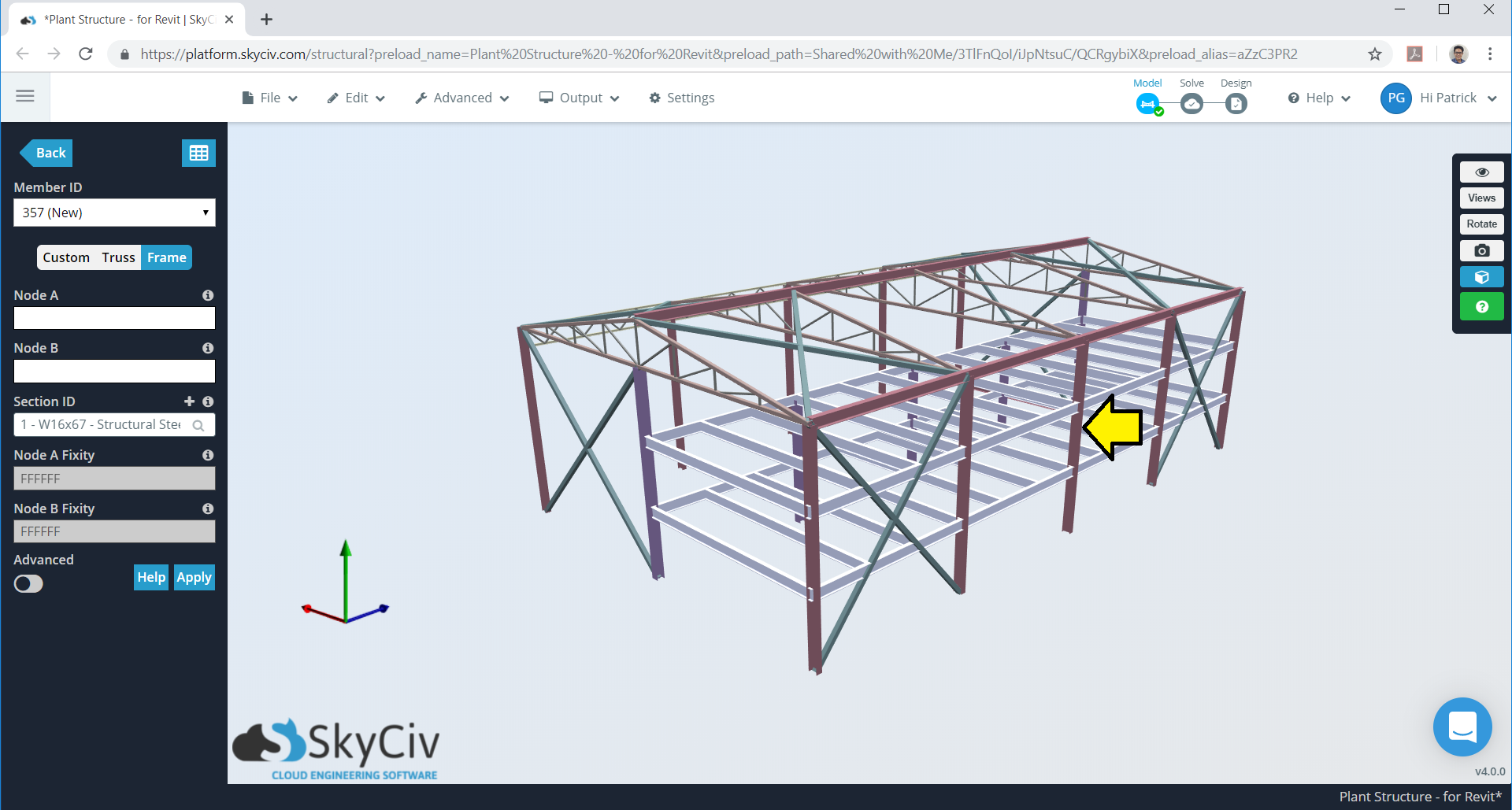
Abbildung 10. Innenrahmen zu berücksichtigen.
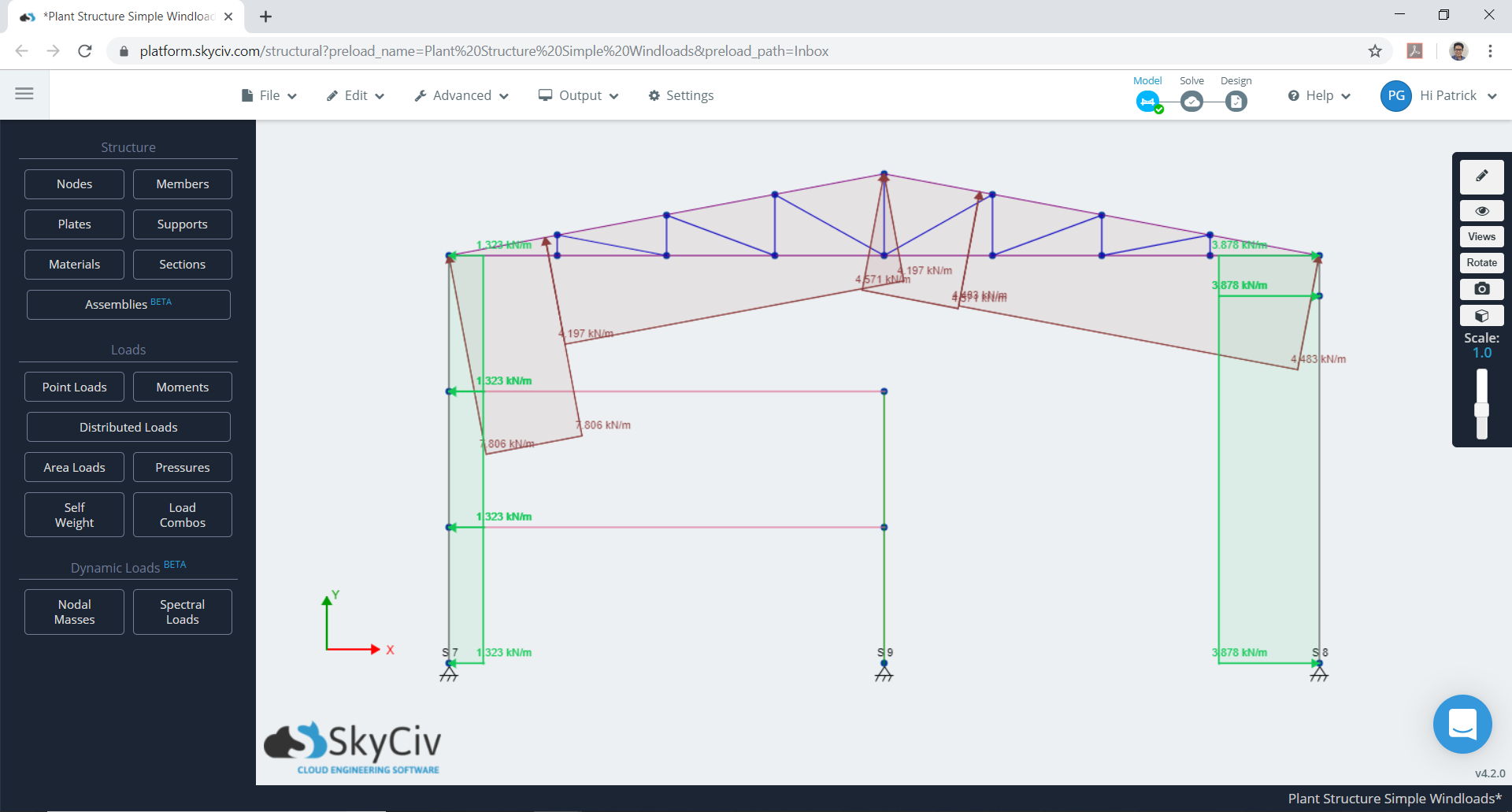
Abbildung 11. Mindestfall für kombiniert \({w}_{e}\) und \({w}_{ich}\).
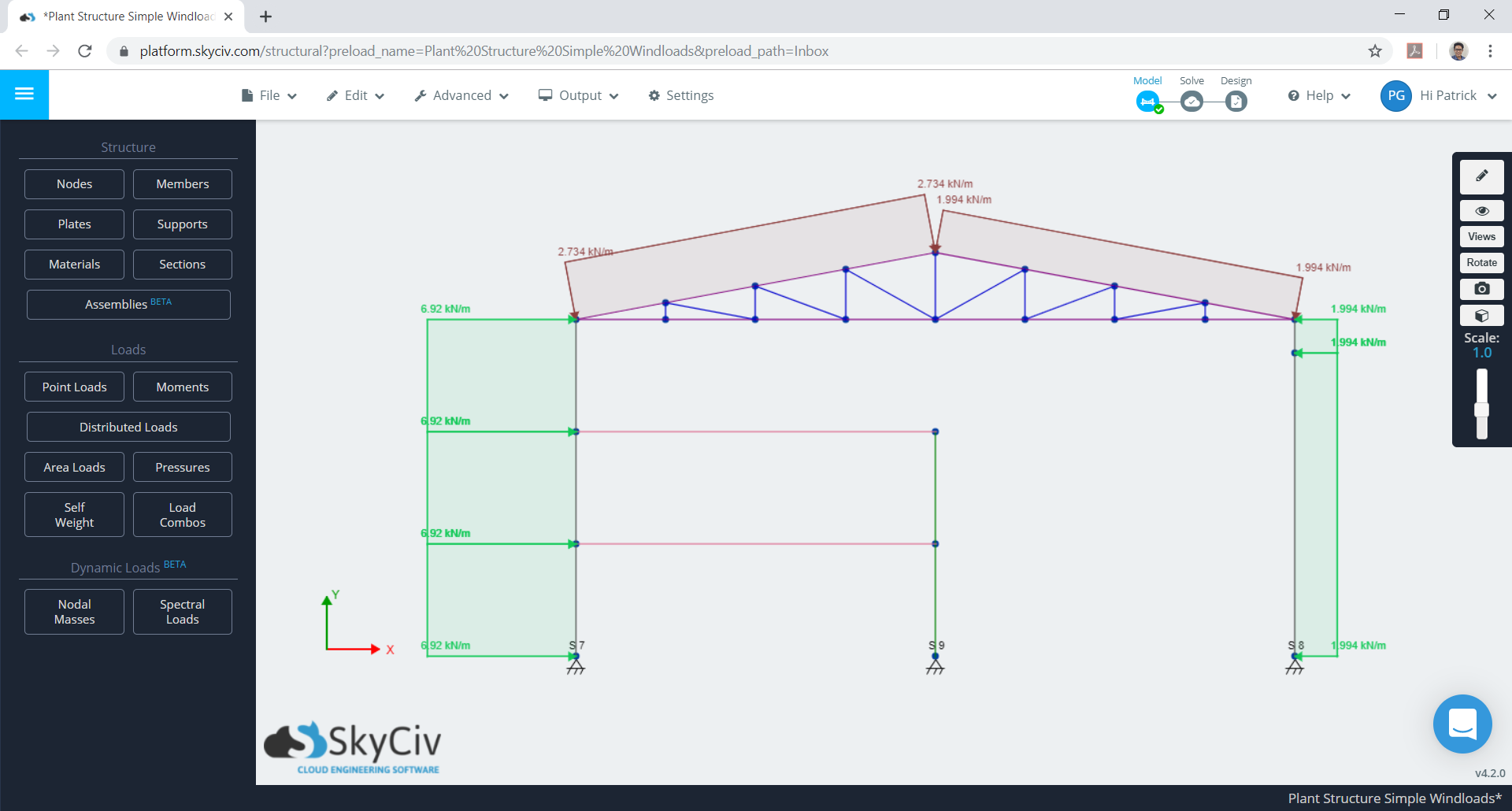
Abbildung 12. Maximaler Fall für kombiniert \({w}_{e}\) und \({w}_{ich}\).
Diese Berechnungen können alle mit durchgeführt werden Windlas-Software von SkyCiv für ASCE 7-10, 7-16, IM 1991, NBBC 2015 und 1170. Benutzer können einen Standort eingeben, um Windgeschwindigkeiten und Topografiefaktoren abzurufen, Gebäudeparameter eingeben und Winddrücke erzeugen. Mit einem professionellen Konto, Benutzer können dies automatisch auf ein Strukturmodell anwenden und die Strukturanalyse in einer einzigen Software ausführen.
Andernfalls, Versuchen unsere SkyCiv Free Wind Tool für Windgeschwindigkeits- und Winddruckberechnungen an einfachen Strukturen.
Statiker, Produktentwicklung
MS Bauingenieurwesen
Verweise:
- Im, B.. (2005). Eurocode 1: Aktionen auf Strukturen - Teil 1–4: Allgemeine Aktionen - Windaktionen.
- DIN EN 1991‐1‐4. (2005). Eurocode 1: Einwirkungen auf Tragwerke Teil 1‐4: Allgemeine Einwirkungen, Windlasten; Deutsche Fassung EN 1991‐1‐4: 2005.



