Ein voll funktionsfähiges Beispiel für AS / NZS 1170.2 Windlastberechnungen
SkyCivs Windlastrechner hat jetzt mehrere Codereferenzen, einschließlich der australischen/neuseeländischen Standards. In diesem Artikel, Wir werden den Auslegungswinddruck für eine Lagerstruktur berechnen. Wir werden ein Modell aus unserem S3D verwenden, um zu demonstrieren, wie die Lasten sind (AS 1170.2 / NZS1170.2 ) werden auf jede Oberfläche aufgetragen.
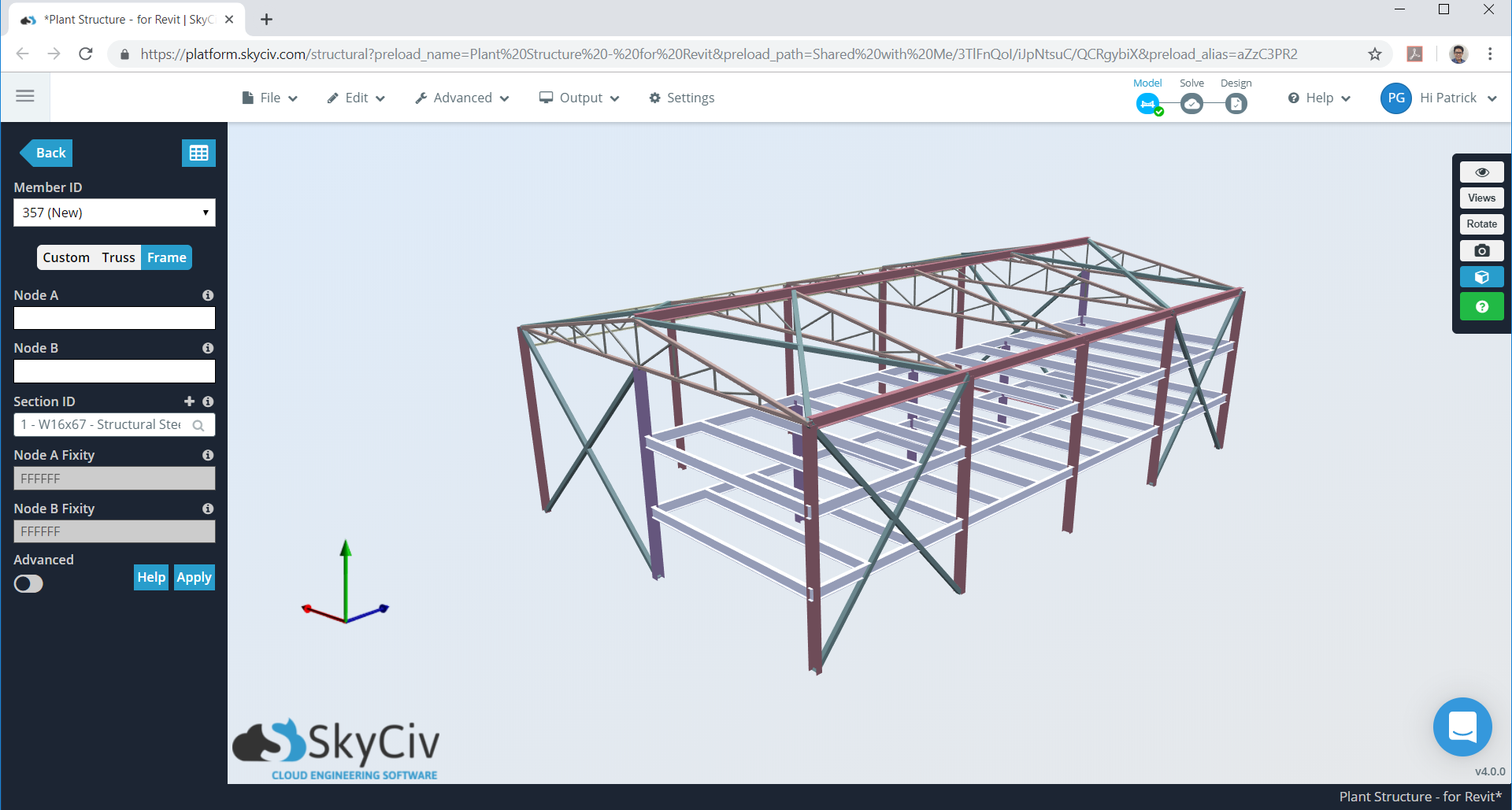
Zahl 1. Beispiel ein Lagermodell in SkyCiv S3D.
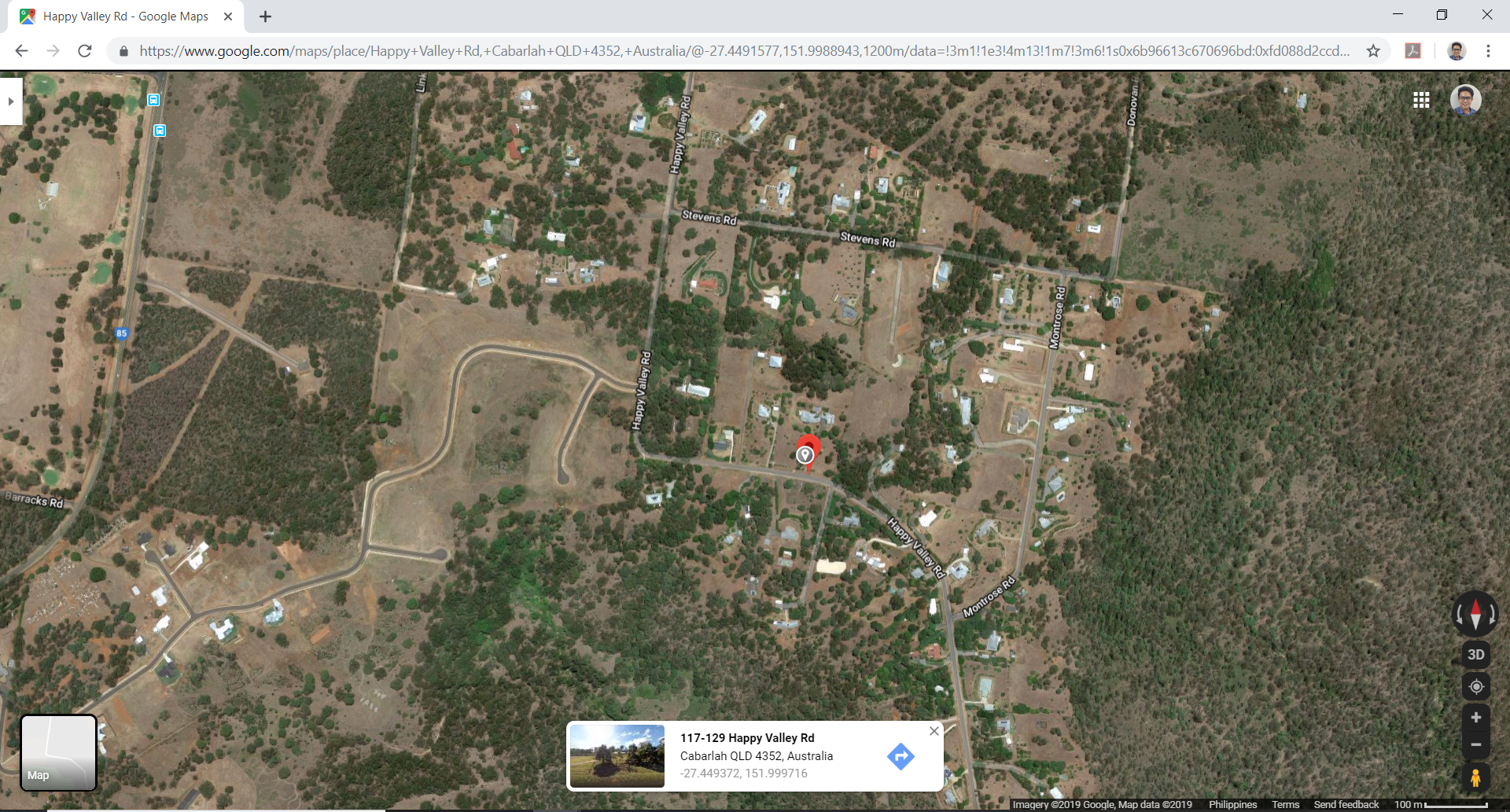
Zahl 2. Standort (von Google Maps).
Tabelle 1. Gebäudedaten, die für unsere Windberechnung benötigt werden.
| Ort | Happy Valley Road, Fordere dich heraus, Queensland, Australien |
| Belegung | Verschiedenes – Lagerstruktur |
| Terrain | Flaches Ackerland |
| Maße | 19.507 m (L.) × 31.699 m (B.) Im Plan Traufhöhe von 9.144 m Scheitelhöhe in der Höhe. 10.973 m Dachneigung 3:16 (10.62°) Ohne zu öffnen |
| Verkleidung | Pfetten beabstandet bei 0.6 m Wandpfosten im Abstand von 0.6 m |
Die Formel zur Bestimmung des Auslegungswinddrucks lautet:
Für Design Windgeschwindigkeit:
\({V }_{sitzen,b} = {V }_{R.} {M.}_{d} {M.}_{mit,Katze} {M.}_{s} {M.}_{t} \) (1)
Wo:
\({V }_{sitzen,b}\) = Auslegungswindgeschwindigkeit in m / s
\({V }_{R.}\) = regionale 3s Böenwindgeschwindigkeit (von der Windkarte), Frau (AS / NZS 1170.2 Sektion 3)
\({M.}_{d}\)= Windrichtungsmultiplikator für 8 Himmelsrichtungen (b) (AS / NZS 1170.2 Sektion 3)
\({M.}_{mit,Katze}\) = Gelände- / Höhenmultiplikator (AS / NZS 1170.2 Sektion 4)
\({M.}_{s}\)= Abschirmmultiplikator, einstellen 1.0 (AS / NZS 1170.2 Sektion 4)
\({M.}_{t}\)= topographischer Multiplikator (AS / NZS 1170.2 Sektion 3)
Für Design Winddruck:
\(p = 0.5 {⍴}_{Luft} ({V }_{von,θ})^ 2 {C.}_{Feige} {C.}_{Mann} \) (2)
Wo:
\(p ) = Auslegungswinddruck in Pa
\({⍴}_{Luft}\) = Luftdichte (1.2 kg / cu.m.)
\({V }_{von,θ}\)= Gebäude orthogonale Windgeschwindigkeiten
\({C.}_{Mann}\)= dynamischer Antwortfaktor, einstellen 1.0
\({C.}_{Feige}\) = aerodynamischer Formfaktor (für inneren oder äußeren Druck) für geschlossene Gebäude wo:
\({C.}_{Feige,ich} = {C.}_{p,ich} {K.}_{c,ich} \) – für Innendrücke (3)
\({C.}_{Feige,e} = {C.}_{p,e} {K.}_{ein} {K.}_{c,e} {K.}_{l} {K.}_{p}\) – für äußere Drücke (4)
\({C.}_{p,ich}\) = Innendruckkoeffizient
\({K.}_{c,ich}\) = Kombinationsfaktor für Innendrücke
\({C.}_{p,e}\) = externer Druckkoeffizient
\({K.}_{ein}\) = Flächenreduzierungsfaktor
\({K.}_{c,e}\) = Kombinationsfaktor für Außendrücke
\({K.}_{l}\) = lokaler Druckfaktor
\({K.}_{p}\) = poröser Mantelfaktor
Jeder Parameter wird nachfolgend erläutert.
Regionale Windgeschwindigkeit, \({V }_{R.}\)
Die regionalen Windgeschwindigkeitsdaten sind in Abbildung dargestellt 3.1 der AS / NZS 1170.2 (wie in den Figuren gezeigt 3 sowie 4 unten). Jeder Verwaltungsbereich wird in Windgeschwindigkeitsbereiche mit entsprechender Windgeschwindigkeit eingeteilt. Für unser Beispiel, Die Site befindet sich in der Nähe des roten Punkts und ist als klassifiziert Region A4 da ist es ungefähr 106 km von der geglätteten Küste der australischen Hauptinsel entfernt. Die entsprechende Windgeschwindigkeit kann anhand der Tabelle berechnet werden 3.1 von AS / NZS 1170.2 wie in Abbildung gezeigt 5. Das jährliche Wiederholungsintervall wird in Abhängigkeit von der Wichtigkeit und der Lebensdauer der Struktur ausgewählt, wie in der Tabelle angegeben 3.3 von AS / NZS 1170.0.
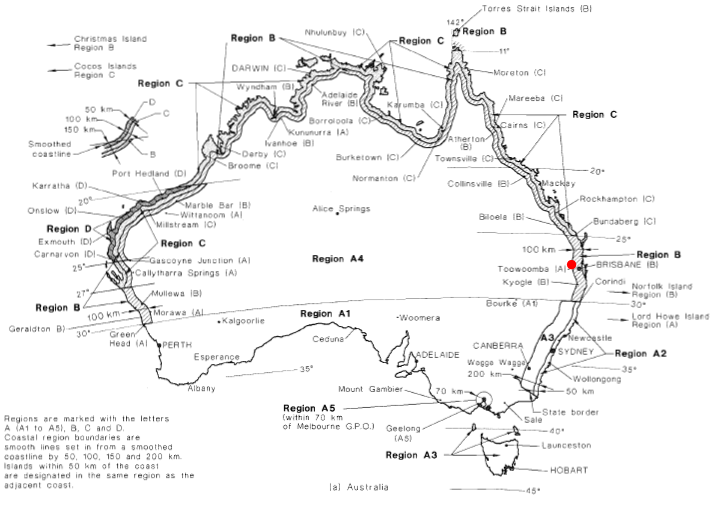
Zahl 3. Regionale Windgeschwindigkeitskarte für Australien (Zahl 3.1(A) von AS / NZS 1170.2).
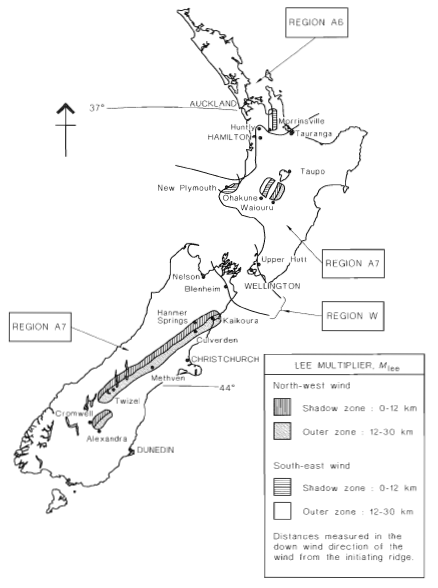
Zahl 4. Regionale Windgeschwindigkeitskarte für Neuseeland (Zahl 3.1(B.) von AS / NZS 1170.2).
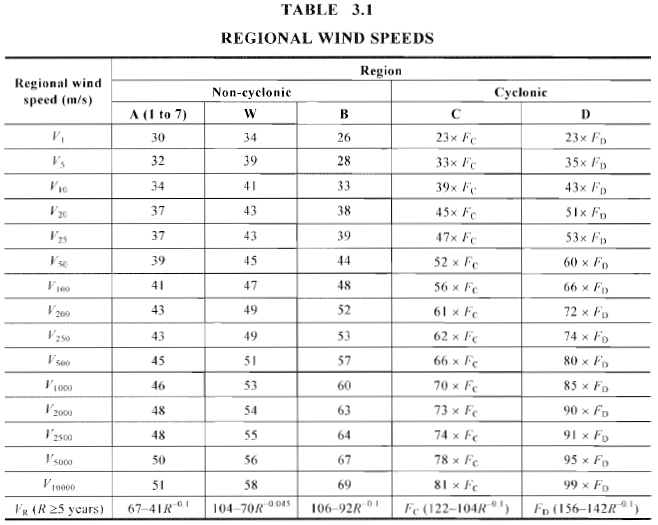
Zahl 5. Entsprechende Windgeschwindigkeit basierend auf Windregion und jährlichem Wiederholungsintervall (Tabelle 3.1 von AS / NZS 1170.2).
Für Endzustände oder Grenzzustände der Gebrauchstauglichkeit, Tabellen 3.1 sowie 3.3 von AS / NZS 1170.0 (Zahlen 6 sowie 7) Einzelheiten zur Klassifizierung der Struktur nach Wichtigkeitsgrad und entsprechender jährlicher Überschreitungswahrscheinlichkeit.
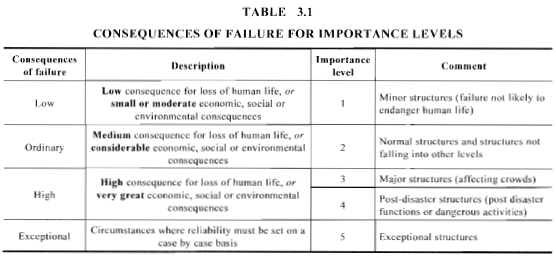
Zahl 6. Definition des Wichtigkeitsgrades gemäß Tabelle 3.1 von AS / NZS 1170.0.
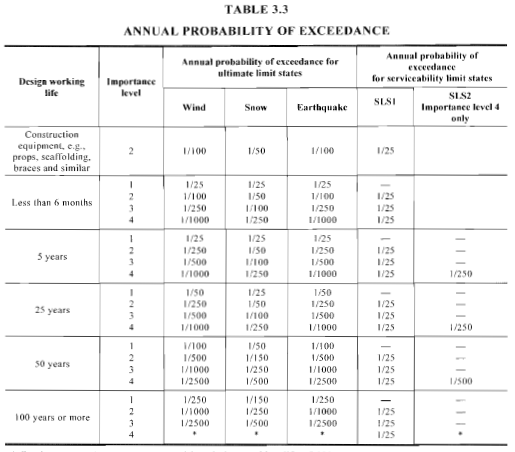
Zahl 7. Definition der jährlichen Überschreitungswahrscheinlichkeit gemäß Tabelle 3.3 von AS / NZS 1170.0.
Für unser Beispiel, Wir werden nur den endgültigen Grenzzustand betrachten. Unsere Beispielstruktur ist klassifiziert nach “gewöhnliche” und angenommen, Design-Lebensdauer von zu haben 50 Jahre. Daher, Wir werden die jährliche Überschreitungswahrscheinlichkeit von gleich annehmen 1/500. Daher, der entsprechende Wert unserer \({V }_{R.}\) ist 45 Frau.
SkyCiv automatisiert jetzt die Erkennung von Windregionen und das Abrufen des entsprechenden Windgeschwindigkeitswerts mit nur wenigen Eingaben. Versuchen unsere SkyCiv Free Wind Tool
Windrichtungsmultiplikator, \({M.}_{d}\)
Für jede Windregion und die entsprechende Windrichtung (8 Himmelsrichtungen), Windrichtungsmultiplikator, \({M.}_{d}\), unterscheiden sich in den Werten, wie in der Tabelle gezeigt 3.2 von AS / NZS 1170.2.
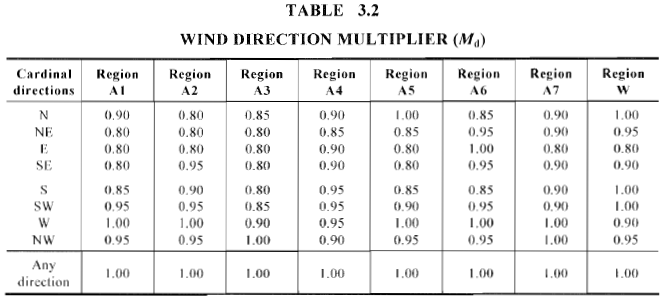
Zahl 8. Windrichtungsmultiplikatorwerte pro Windbereich und Richtung gemäß Tabelle 3.2 von AS / NZS 1170.2.
Für dieses Beispiel, Wir werden die Windgeschwindigkeit überprüfen, von der wir kommen “GEBOREN” in welchem \({M.}_{d}\) = 0.85. jedoch, es ist auch sicher anzunehmen \({M.}_{d}\) = 1.0 ein konservatives Ergebnis geben.
Gelände- / Höhenmultiplikator, \({M.}_{mit,Katze}\)
Um den Gelände- / Höhenmultiplikator zu berechnen \({M.}_{mit,Katze}\), Wir müssen die Geländekategorie unserer Site klassifizieren. Tabelle 2 zeigt die Definition jeder Geländekategorie basierend auf Abschnitt 4.2.1 von AS / NZS 1170.2. \({M.}_{mit,Katze}\) kann jetzt mit Tabelle berechnet werden 4.1 von AS / NZS 1170.2 abhängig von der Höhe, Windregion und Geländekategorie der Struktur.
Tabelle 2. Definition der Geländekategorie für AS / NZS 1170.2.
| Geländekategorie | Definition |
|---|---|
| Kategorie 1 | Freiliegendes offenes Gelände mit wenigen oder keinen Hindernissen und Wasseroberflächen bei Windgeschwindigkeiten |
| Kategorie 2 | Wasseroberflächen, offenes Gelände, Grünland mit wenigen, gut verstreute Hindernisse mit Höhen im Allgemeinen von 1.5 m bis 10 m |
| Kategorie 3 | Gelände mit zahlreichen eng beieinander liegenden Hindernissen 3 m bis 5 m hoch, wie Bereiche von Vorortwohnungen. |
| Kategorie 4 | Gelände mit zahlreichen großen, hoch (10 m bis 30 m hoch) und eng beieinander liegende Hindernisse, wie große Stadtzentren und gut entwickelte Industriekomplexe. |
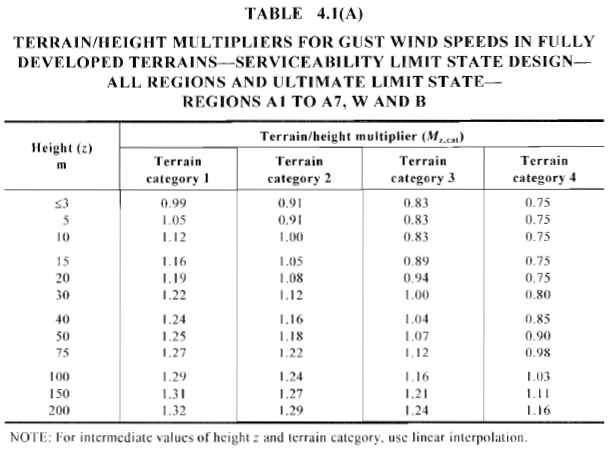
Zahl 9. Berechneter Gelände- / Höhenmultiplikator, \({M.}_{mit,Katze}\) , basierend auf der entsprechenden Geländekategorie und Windregion (Tabelle 4.1 von AS / NZS 1170.2).
Für unser Beispiel, Der Standort kann als klassifiziert werden “Kategorie 2” vorausgesetzt, wir haben für jede Windrichtung eine einheitliche Geländekategorie. Wir werden die Höhe der Struktur für jeweils 3 m und die mittlere Dachhöhe teilen. Die tabellarischen Werte von \({M.}_{mit,Katze}\) für jede Ebene ist in der Tabelle gezeigt 3.
Tabelle 3. Berechnet \({M.}_{mit,Katze}\) für jede Ebene der Struktur.
| Höhe, m | \({M.}_{mit,Katze}\) |
|---|---|
| 3 m | 0.91 |
| 6 m | 0.928 |
| 9 m | 0.982 |
| 10.06 m | 1.001 |
Abschirmmultiplikator, \({M.}_{s}\)
Der Abschirmeffekt kann bei der Berechnung der Auslegungswinddrücke mit AS / NZS berücksichtigt werden 1170.2. Dies ist zu berücksichtigen, um den Winddruck zu verringern, wenn nahegelegene Strukturen vorhanden sind. Sektion 4.3 von AS / NZS 1170.2 Einzelheiten zur Berechnung des Abschirmfaktors \({M.}_{s}\). Für dieses Beispiel, da der Standort in einem offenen Feld liegt, und nahe gelegene Strukturen haben einen Abstand von mehr als 20 Stunden (201.2 m) von der Struktur, wir können das annehmen \({M.}_{s}\) = 1.0.
Topographischer Multiplikator, \({M.}_{t}\)
Der Einfluss der Topographie auf den Winddruck wird im topografischen Multiplikator erfasst, \({M.}_{t}\), wo es den Auslegungswinddruck basierend auf der Bodenhöhe des Standorts verstärkt, ob sich die Struktur auf einem Hügel oder einer Böschung befindet. Sektion 4.4 der AS / NZS 1170.2 Einzelheiten zur Berechnung dieses Parameters. Außerhalb der lokalen topografischen Zone, eine berechnete Entfernung vom Gipfel des Hügels oder der Böschung, bleibt die \({M.}_{t}\) kann als gleich angesehen werden 1.0 wie in den Figuren gezeigt 4.2 sowie 4.3 von AS / NZS 1170.2 (Zahl 10).
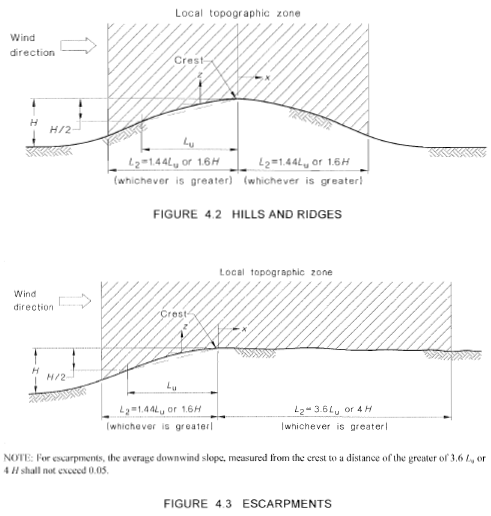
Zahl 10. Parameter, die zur Berechnung des topografischen Faktors benötigt werden, \({M.}_{t}\) , basierend auf Abschnitt 4.4 von AS / NZS 1170.2.
Aus den Bodenhöhendaten des Standorts (von Google Maps, kommt aus NE), Wir schließen daraus, dass die Topographie als Hügel klassifiziert werden kann. Basierend auf Abbildung 4.2 von AS / NZS 1170.2, Die folgenden Punkte können wie in der Tabelle gezeigt erhalten werden 4:
Tabelle 4. Extrahierte Datenpunkte aus Bodenhöhendaten (von Google Maps) wie in Abbildung gezeigt 11.
| Parameter | Wert |
| M.t | 1.076 |
| Steigung | 0.07 |
| Lage des Gipfels | -380.00 m vom Ort der Struktur |
| Höhe des Gipfels | 628.16 m |
| Lage des Fußes | -2000.00 m vom Ort der Struktur |
| Fußhöhe | 515.37 m |
| H. | 112.79 m |
| Platz. von H / 2 | -1154.23 m vom Ort der Struktur |
| x | 380.00 m |
| L.u | 774.23 m |
| L.1 | 278.72 m |
| L.2 | 1114.89 m |
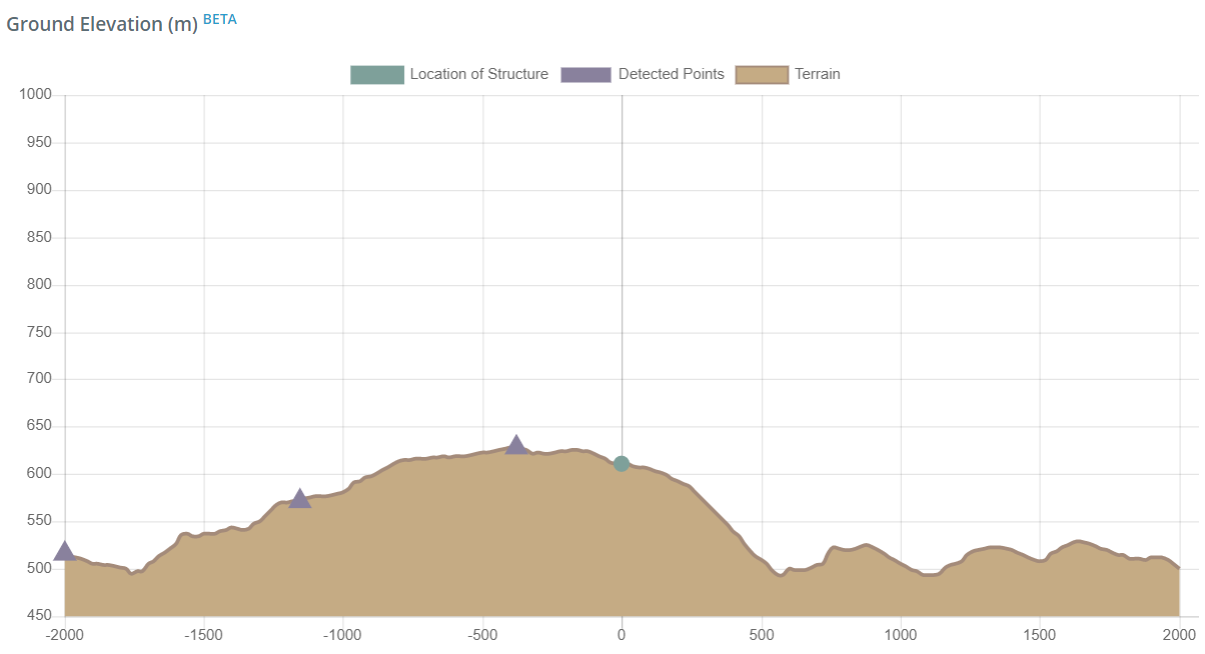
Zahl 11. Bodenhöhe des Standorts im NE-SW-Abschnitt (von Google Maps).
Aus den in der Tabelle gezeigten Daten 4, der berechnete topografische Multiplikator, \({M.}_{t}\), entspricht 1.08 basierend auf Gleichung 4.4(2) von AS / NZS 1170.2 wie in Gleichung gezeigt (5).
\({M.}_{t} = {M.}_{h} = 1 + [ H. / 3.5(mit + {L.}_{1})] [ 1 – ( |x| / {L.}_{2})] \) (5)
\({M.}_{t} = 1.08 \)
Schließlich, unter Verwendung von Gleichung (1), Die berechnete Auslegungswindgeschwindigkeit ist in der Tabelle angegeben 5.
Tabelle 5. Berechnet \({V }_{sitzen,b}\) für jede Ebene der Struktur.
| Höhe, m | \({V }_{sitzen,b}\), Frau |
| 3 | 37.45 |
| 6 | 38.19 |
| 9 | 40.42 |
| 10.06 | 41.20 |
Wo:
\({V }_{sitzen,b (Minimum)}\) = 30 m / s für dauerhafte Strukturen und 25 m / s für temporäre Strukturen (Lebensdauer ≤ 5 Jahre)
Zur Berechnung der Auslegungswinddrücke, die aerodynamischen Formfaktoren, \({C.}_{Feige}\), für Innen- und Außenflächen werden benötigt. Dies wird im nächsten Abschnitt erläutert.
Aerodynamischer Formfaktor, \({C.}_{Feige}\)
Der aerodynamische Formfaktor, \({C.}_{Feige}\), wird verwendet, um die Werte des Winddrucks zu bestimmen, der auf jede Oberfläche ausgeübt wird. Ein positiver Wert von \({C.}_{Feige}\) bedeutet, dass der Druck auf die Oberfläche wirkt, während negativ bedeutet, dass er von der Oberfläche weg wirkt.
Aerodynamischer Formfaktor für Innendruck, \({C.}_{Feige,ich}\)
Innendruckkoeffizient, \({C.}_{p,ich}\)
Zum \({C.}_{Feige,ich}\), die Berechnung des Innendruckkoeffizienten \({C.}_{p,ich}\) ist in der Tabelle aufgeführt 5.1 von AS / NZS 1170.2 wie in Abbildung gezeigt 12.
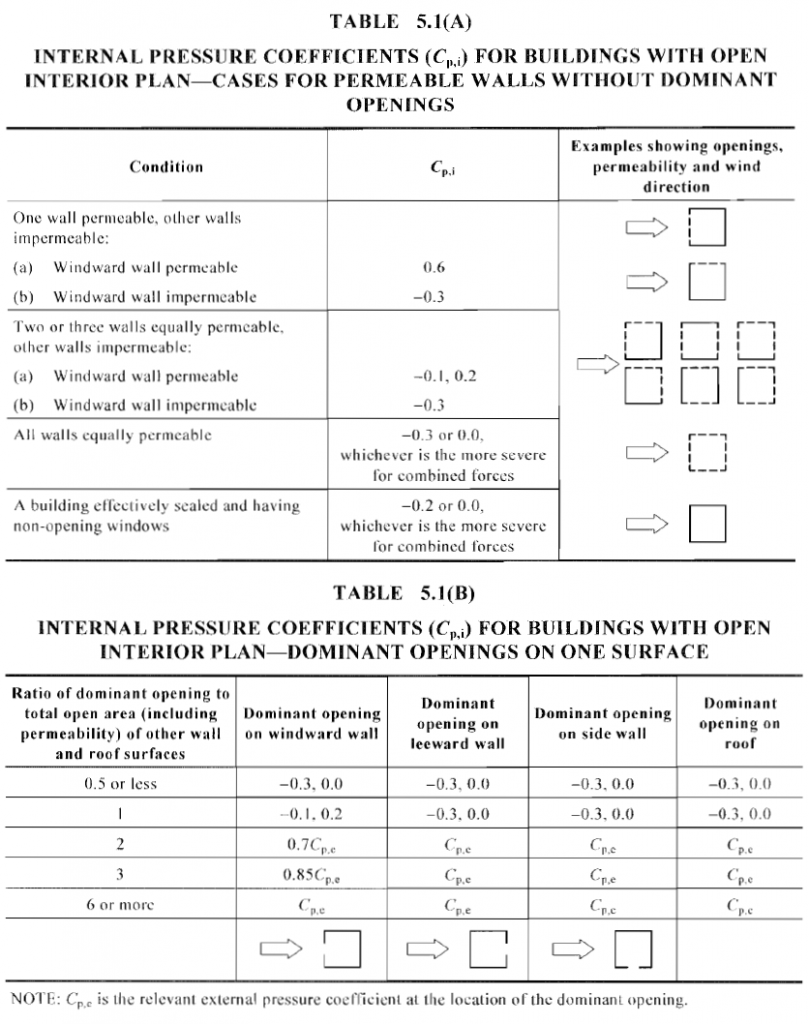
Zahl 12. Innendruckkoeffizient, \({C.}_{p,ich}\), wie in Abschnitt definiert 5.3 von AS / NZS 1170.2.
Für dieses Beispiel, Unsere Struktur ist geschlossen und es wird angenommen, dass sie keine Öffnung hat, daher, Voraussetzung dafür ist die Struktur “Ein Gebäude, das effektiv skaliert ist und nicht öffnende Fenster hat” und die entsprechenden Innendruckkoeffizienten sind \({C.}_{p,ich}\) = -0.2, 0.0.
Aerodynamischer Formfaktor für den Außendruck, \({C.}_{Feige,e}\)
Externer Druckkoeffizient, \({C.}_{p,e}\)
Sektion 5.4 von AS / NZS 1170.2 definiert das Verfahren zum Ermitteln des externen Druckkoeffizienten, \({C.}_{p,e}\), für rechteckige Gebäude. Gebäudeflächen für die Außendruckverteilung sind in Abbildung definiert 5.2 des Codes wie in Abbildung gezeigt 13. Außerdem, Tabellen 5.2 zu 5.3 von AS / NZS 1170.2 Einzelheiten zu den berechneten Werten von \({C.}_{p,e}\) für jede Oberflächendefinition wie in den Figuren gezeigt 14 zu 18.
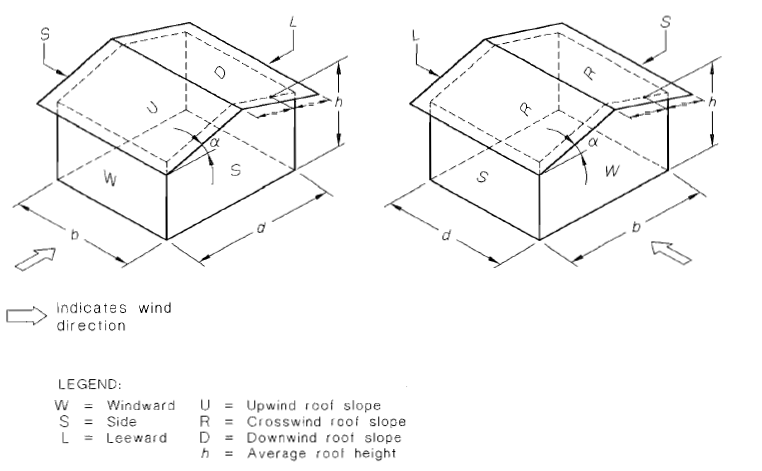
Zahl 13. Oberflächendefinition für die externe Druckverteilung, wie in Abschnitt definiert 5.4 von AS / NZS 1170.2.
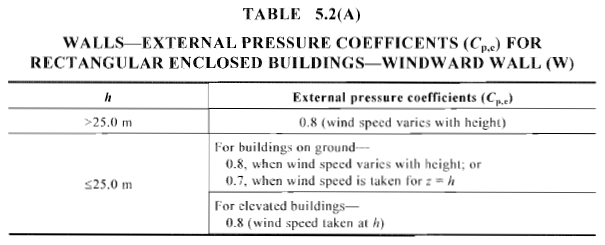
Zahl 14. Berechneter Außendruckkoeffizient, \({C.}_{p,e}\), für die Luvwand rechteckiger geschlossener Gebäude (Tabelle 5.2(A) von AS / NZS 1170.2).
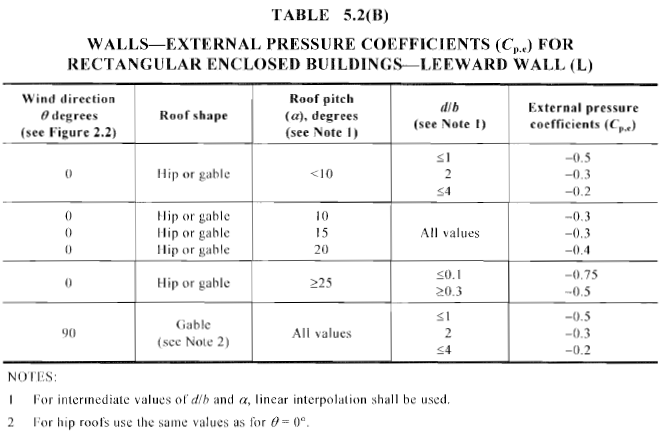
Zahl 15. Berechneter Außendruckkoeffizient, \({C.}_{p,e}\), für Lee-Wand von rechteckigen geschlossenen Gebäuden (Tabelle 5.2(B.) von AS / NZS 1170.2).
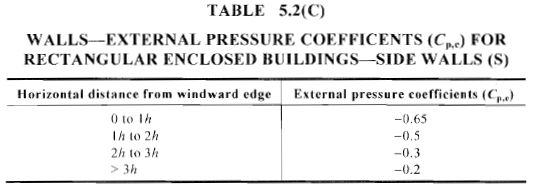
Zahl 16. Berechneter Außendruckkoeffizient, \({C.}_{p,e}\), für Seitenwände von rechteckigen geschlossenen Gebäuden (Tabelle 5.2(C.) von AS / NZS 1170.2).
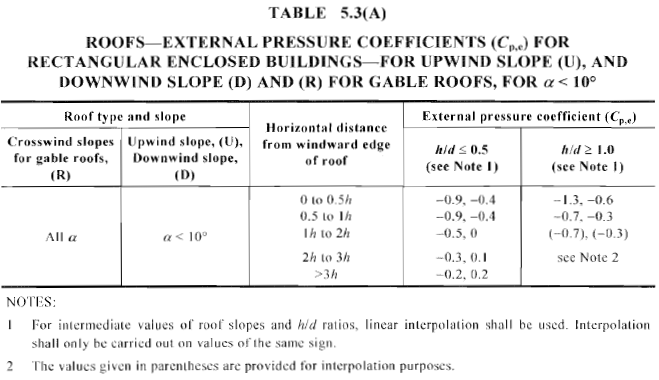
Zahl 17. Berechneter Außendruckkoeffizient, \({C.}_{p,e}\), für Auf- und Abwindfläche des Satteldachs mit Neigungswinkel < 10° (Tabelle 5.3(A) von AS / NZS 1170.2).
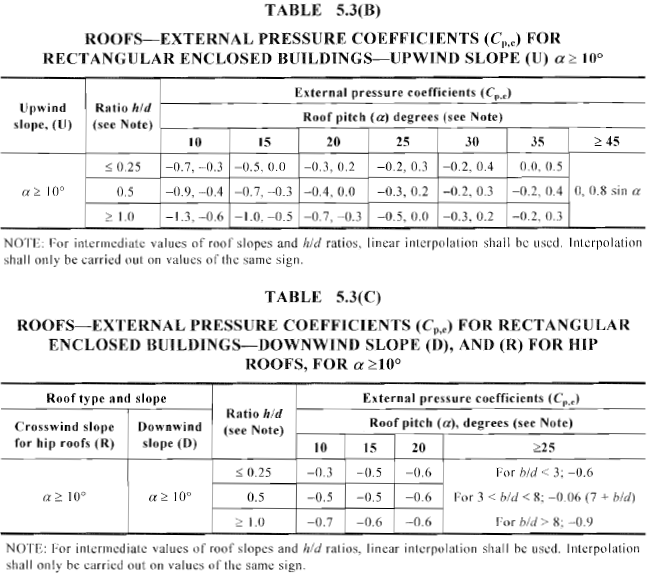
Zahl 18. Berechneter Außendruckkoeffizient, \({C.}_{p,e}\), für Aufwind- und Abwindfläche von Giebel- und Walmdach mit Neigungswinkel ≥ 10° (Tabelle 5.3(A) und Tabelle 5.3(B.) von AS / NZS 1170.2).
Für dieses Beispiel, \({C.}_{p,e}\) Werte für Wandflächen sind in der Tabelle aufgeführt 6 sowie 7 unten wo \(d/b\) = 0.616 für 0° und \(b / d ) = 1.625 für 90° , \(h / d ) = 0.516, sowie \(h/b\) = 0.317 . Außerdem, Tabelle 8 zeigt die \({C.}_{p,e}\) Werte für Dachflächen.
Tabelle 6. Berechnete Außendruckkoeffizienten, \({C.}_{p,e}\), für Wandflächen in Luv- und Lee-Richtung.
| Höhe, m | \({C.}_{p,e}\) (Luv) | \({C.}_{p,e}\) (Lee-) - entlang L. (0°) |
\({C.}_{p,e}\) (Lee-) - entlang B. (90°) |
| 3 | 0.8 | -0.3 | -0.375 |
| 6 | 0.8 | ||
| 9 | 0.8 | ||
| 10.06 | 0.7 |
Tabelle 7. Berechnete Außendruckkoeffizienten, \({C.}_{p,e}\), für Seitenwandflächen.
| Lage von der Luvwand, m | \({C.}_{p,e}\) (Seitenwand) |
| 0 bis 10,06 m | -0.65 |
| 10.06 zu 19.507 m | -0.50 |
Tabelle 8. Berechnete Außendruckkoeffizienten, \({C.}_{p,e}\), für Dachflächen.
| Dachfläche | \({C.}_{p,e}\) |
| Gegen den Wind | -0.888, -0.394 |
| Gegen den Wind | -0.503 |
| Seitenwind | -0.9, -0.4 (0 zu h) -0.5, 0.0 (h bis 2h) -0.3, 0.1 (2h bis 3h) -0.2, 0.2 (> 3h) |
Flächenreduzierungsfaktor, \({K.}_{ein}\)
Flächenreduzierungsfaktor, \({K.}_{ein}\), gilt nur für Seitenwände und Dachflächen. Ansonsten berechnet, \({K.}_{ein}\) ist immer gleich 1.0. Tabelle 5.4 von AS / NZS 1170.2 zeigt den Wert von \({K.}_{ein}\) abhängig von der beitragenden Fläche für Seitenwände und Dachflächen, wie in Abbildung gezeigt 19.

Zahl 19. Werte des Flächenreduzierungsfaktors, \({K.}_{ein}\), für Seitenwände und Dachflächen (Tabelle 5.4 von AS / NZS 1170.2).
Für unser Beispiel, Die berechneten Werte des Flächenreduzierungsfaktors sind in der Tabelle gezeigt 9 unten.
Tabelle 9. Werte des Flächenreduzierungsfaktors, \({K.}_{ein}\), für dieses Beispiel.
| Oberfläche | Bereich, qm. | \({K.}_{ein}\) |
| Seitenwand (entlang d) | 196.21 | 0.8 |
| Seitenwand (entlang b) | 285.29 | 0.8 |
| Dach – Luv | 314.564 | 0.8 |
| Dach – Lee- | 314.564 | 0.8 |
| Dach – Seitenwind | 629.129 | 0.8 |
Lokaler Druckfaktor für Verkleidungen, \({K.}_{l}\)
Der lokale Druckfaktor, \({K.}_{l}\), ist immer gleich 1.0 auf allen Oberflächen außer Bauteilen und Verkleidungen. Sektion 5.4.4 von AS / NZS 1170.2 Einzelheiten zum Berechnungsverfahren beim Abrufen \({K.}_{l}\) für diese Komponenten.
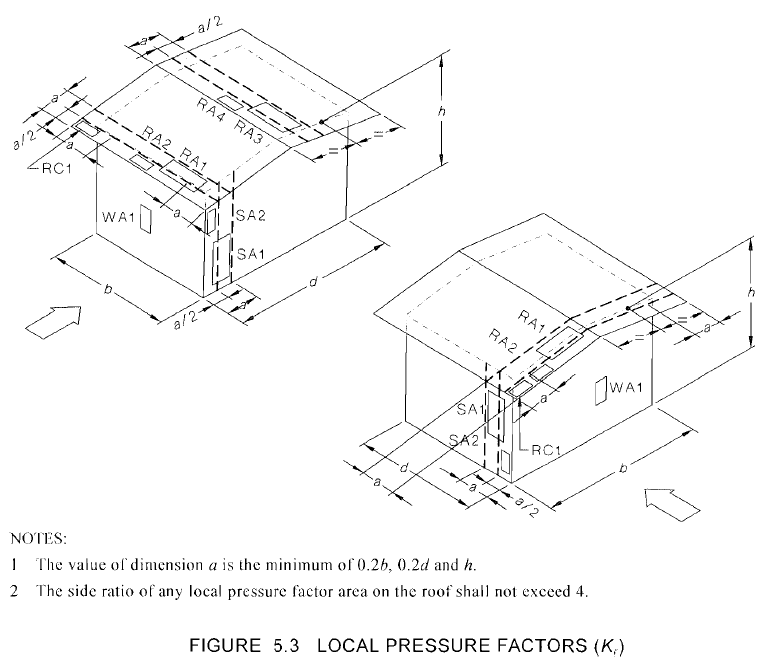
Zahl 20. Position der Plattierungsdrücke wie in der Tabelle definiert 5.6 von AS / NZS 1170.2.
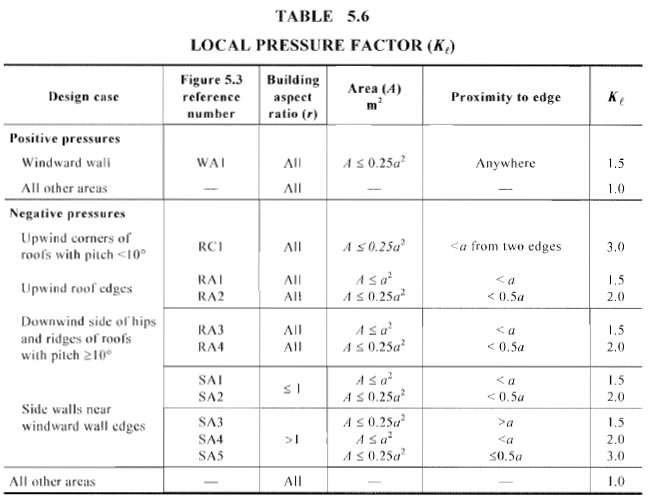
Zahl 21. Werte des lokalen Druckfaktors, \({K.}_{l}\), für jede Zone wie in Abbildung gezeigt 20.
Für dieses Beispiel, die Werte von \(ein) ist das Minimum von \(0.2b\) (3.91 m), \(02.d\) (6.34 m), oder \(h ) (10.06m), daher, \(ein) = 3.91 m. Die entsprechende Fläche und der lokale Druckfaktor für Pfetten und Wandpfosten sind in der Tabelle aufgeführt 10 unten mit der Annahme, dass die Spannweite der Pfette gleich dem Abstand der Traversen ist (7.924 m) und die Spannweite der Wandpfosten entspricht der Geschosshöhe (3 m). Das Gebäude-Seitenverhältnis ist das größte von \(h / d ) (0.516) sowie \(h/b\) (0.317).
Tabelle 10. Werte des lokalen Druckfaktors \({K.}_{l}\) für Pfetten und Wandpfosten.
| Verkleidung | Bereich, qm. | Zonen | Kl für Überdruck | Kl für Unterdruck |
| Pfette | 4.75 | RA1 | 1.0 | 1.5 |
| RA3 | 1.0 | 1.5 | ||
| Wandpfosten | 1.80 | WA1 | 1.0 | 1.0 |
| SA1 | 1.0 | 1.5 | ||
| SA2 | 1.0 | 2.0 |
Reduktionsfaktor für durchlässige Verkleidungen, \({K.}_{p}\), für Dächer und Seitenwände
Der Durchlässigkeitsfaktor für die durchlässige Verkleidung, \({K.}_{p}\), ist immer gleich 1.0 für alle Oberflächen mit der Ausnahme, dass eine Außenfläche aus einer durchlässigen Ummantelung besteht und das Festigkeitsverhältnis kleiner als ist 0.999 wobei das Festigkeitsverhältnis das Verhältnis der festen Fläche zur Gesamtoberfläche ist. Für dieses Beispiel, wir werden das annehmen \({K.}_{p}\) entspricht 1.0.
Aktionskombinationsfaktoren, \({K.}_{c,ich}\) sowie \({K.}_{c,e}\)
Aktionskombinationsfaktoren, \({K.}_{c,ich}\) sowie \({K.}_{c,e}\), werden verwendet, um die Auswirkung der Windlast zu berechnen, die gleichzeitig auf bestimmte Oberflächen wirkt (wie Wind, der auf Wände wirkt, Dächer, und Innendruck). Tabelle 5.5 der AS / NZS 1170.2 zeigt Beispiele für eine Aktionskombination mit ihren entsprechenden Aktionskombinationsfaktoren, wie in Abbildung dargestellt 22.
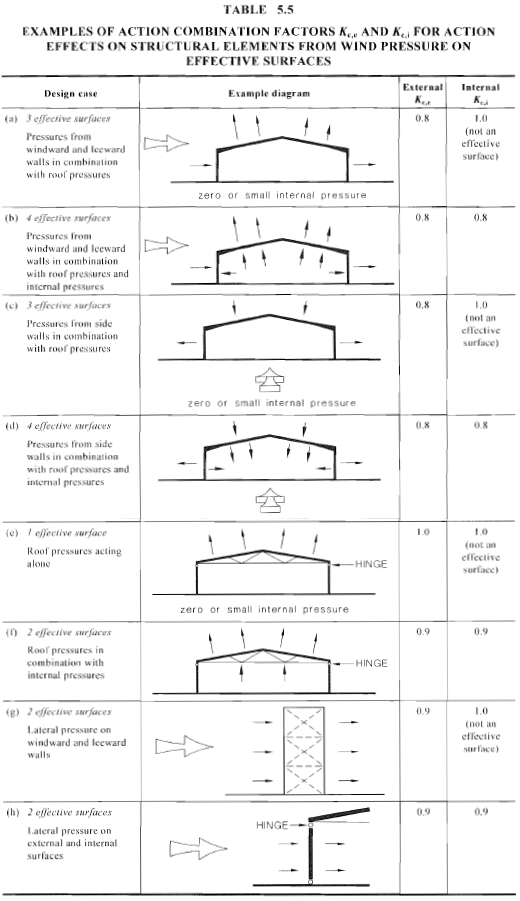
Zahl 22. Aktionskombinationsfaktoren \({K.}_{c,e}\) sowie \({K.}_{c,ich}\) aus der Tabelle 5.5 von AS / NZS 1170.2.
Für dieses Beispiel, Wir werden den Entwurfsfall betrachten (b) wo 4 effektive Oberflächen werden mit Auslegungsdrücken belastet. Daher, \({K.}_{c,ich}\) sowie \({K.}_{c,e}\) sind beide gleich 0.8.
Konstruktionswinddrücke für den Hauptrahmen
Da haben wir schon die notwendigen Parameter, \(p ), Wir können die Auslegungswinddruckwerte unter Verwendung von Gleichungen erhalten (2) zu (4). Tabellen 11 zu 13 Zeigen Sie die Zusammenfassung der Parameter für jede Oberfläche an.
Tabelle 11. Bemessungsdruckwerte für die Luvwand.
| Höhe, m | \({M.}_{mit,Katze}\) | \({V }_{von,θ}\) | \({C.}_{Feige}\) | \({C.}_{p,e}\) | \({K.}_{ein}\) | \({K.}_{c,e}\) | \({K.}_{l}\) | \({K.}_{p}\) | Auslegungsdruck \(p ), Gut |
| 3 | 0.910 | 37.45 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 538.64 |
| 6 | 0.928 | 38.19 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 560.16 |
| 9 | 0.982 | 40.42 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 627.25 |
| 10.06 | 1.001 | 41.20 | 0.560 | 0.7 | 1 | 0.8 | 1 | 1 | 570.29 |
Tabelle 12. Berechnete Auslegungsdruckwerte für Lee und Seitenwände, und Dachflächen.
| Oberfläche | \({V }_{von,θ}\) | \({C.}_{Feige}\) | \({C.}_{p,e}\) | \({K.}_{ein}\) | \({K.}_{c,e}\) | \({K.}_{l}\) | \({K.}_{p}\) | Auslegungsdruck \(p ), Gut |
| Leeward Wand | 41.20 | -0.24 | -0.3 | 1 | 0.8 | 1 | 1 | -244.41 |
| Seitenwand (0 bis 10,06 m) |
-0.520* | -0.65 | 0.8 | 0.8 | 1 | 1 | -529.55 | |
| Seitenwand (0 bis 10,06 m) |
-0.400* | -0.5 | 0.8 | 0.8 | 1 | 1 | -407.35 | |
| Dach (gegen den Wind) |
-0.710* | -0.888 | 0.80 | 0.8 | 1.0 | 1.0 | -723.13 | |
| -0.315* | -0.394 | 0.80 | 0.8 | 1.0 | 1.0 | -320.99 | ||
| Dach (gegen den Wind) |
-0.402* | -0.503 | 0.80 | 0.8 | 1.0 | 1.0 | -409.79 | |
| Dach (Seitenwind) |
-0.720* -0.400* -0.240* -0.160* |
-0.90 -0.50 -0.30 -0.20 |
0.80 0.80 0.80 0.80 |
0.8 0.8 0.8 0.8 |
1.0 1.0 1.0 1.0 |
1.0 1.0 1.0 1.0 |
-733.23 (0 zu h) -407.35 (h bis 2h) -244.41 (2h bis 3h) -162.94 (> 3h) |
Tabelle 13. Berechnete innere Winddrücke, die gleichzeitig mit äußeren Drücken wirken.
* – Produkt von \({K.}_{ein}\) sowie \({K.}_{c,e}\) soll nicht kleiner sein als 0.8 (Sektion 5.4.3 von AS / NZS 1170.2).
| Oberfläche | \({V }_{von,θ}\) | \({C.}_{Feige,ich}\) | \({C.}_{p,ich}\) | \({K.}_{c,ich}\) | Auslegungsdruck \(p ), Gut |
| Interner Druck | 41.20 | 0.0 | 0.0 | 0.8 | 0.0 |
| 41.20 | -0.16 | -0.2 | 0.8 | -162.94 |
Zusammenfassend sind die Auslegungsdrücke in der Tabelle aufgeführt 14 sowie 15 Kombination der Wirkung von äußerer und innerer Druckwirkung.
Tabelle 14. Berechneter Auslegungswinddruck für die Luvwand.
| Höhe, m | Externer Druck \({p}_{e}\), Gut | Interner Druck, Gut | Kombinierter Druck, Gut | ||
| \({p}_{ich,max}\) | \({p}_{ich,Mindest}\) | \({p}_{e}-{p}_{ich,max}\) | \({p}_{e}-{p}_{ich,Mindest}\) | ||
| 3 | 538.64 | 0.00 | -162.94 | 538.64 | 701.58 |
| 6 | 560.16 | 0.00 | -162.94 | 560.16 | 723.10 |
| 9 | 627.25 | 0.00 | -162.94 | 627.25 | 790.19 |
| 10.06 | 570.29 | 0.00 | -162.94 | 570.29 | 733.23 |
Tabelle 15. Berechneter Auslegungswinddruck für andere Oberflächen.
| Oberfläche | Externer Druck \({p}_{e}\), Gut | Interner Druck, Gut | Kombinierter Druck, Gut | ||
| \({p}_{ich,max}\) | \({p}_{ich,Mindest}\) | \({p}_{e}-{p}_{ich,max}\) | \({p}_{e}-{p}_{ich,Mindest}\) | ||
| Leeward Wand | -244.41 | 0.00 | -162.94 | -244.41 | -81.47 |
| Seitenwand (0 bis 10,06 m) | -529.55 | 0.00 | -162.94 | -529.55 | -366.61 |
| Seitenwand (10.06 bis 19.507m) | -407.35 | 0.00 | -162.94 | -407.35 | -244.41 |
| Dach (gegen den Wind) | -723.13 | 0.00 | -162.94 | -723.13 | -560.19 |
| -320.99 | 0.00 | -162.94 | -320.99 | -158.05 | |
| Dach (gegen den Wind) | -409.79 | 0.00 | -162.94 | -409.79 | -246.85 |
| Dach (Seitenwind) | -733.23 (0 zu h) -407.35 (h bis 2h) -244.41 (2h bis 3h) -162.94 (> 3h) |
0.00 | -162.94 | -733.23 (0 zu h) -407.35 (h bis 2h) -244.41 (2h bis 3h) -162.94 (> 3h) |
-570.29 (0 zu h) -244.41 (h bis 2h) -81.47 (2h bis 3h) 0 (> 3h) |
Da der Abstand jedes Rahmens gleich 7,925 m ist, unter Berücksichtigung eines Rahmens, Die äquivalenten verteilten Windlasten, die auf den Rahmen wirken, sind in den Abbildungen dargestellt 23 sowie 24. Beachten Sie, dass zwei Lastfälle zu berücksichtigen sind, und maximale Absolutwerte des Dachaufwinddrucks werden jeweils berücksichtigt.
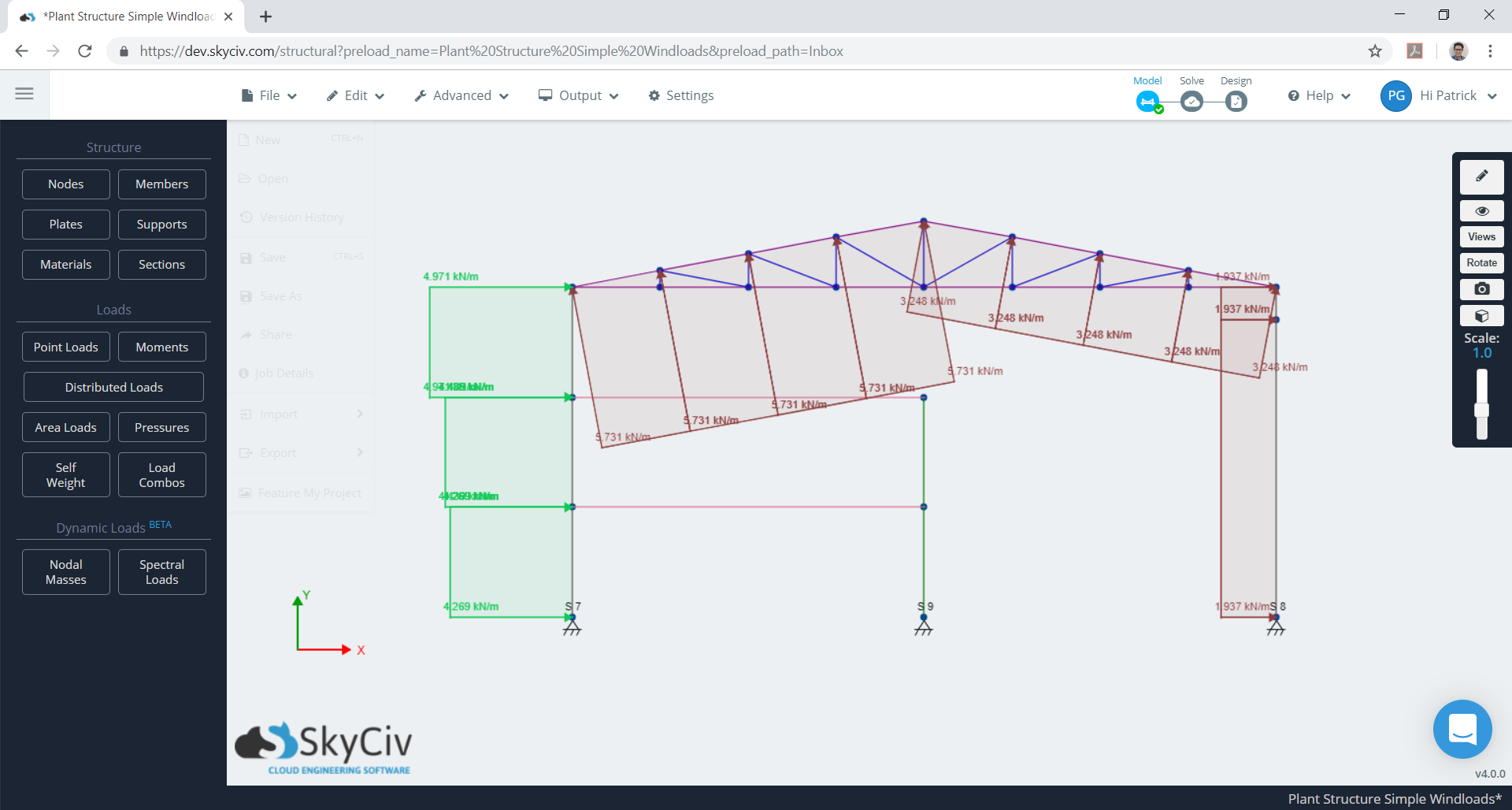
Zahl 23. Äquivalente Auslegungswinddrücke für einen Rahmen (Fall 1).
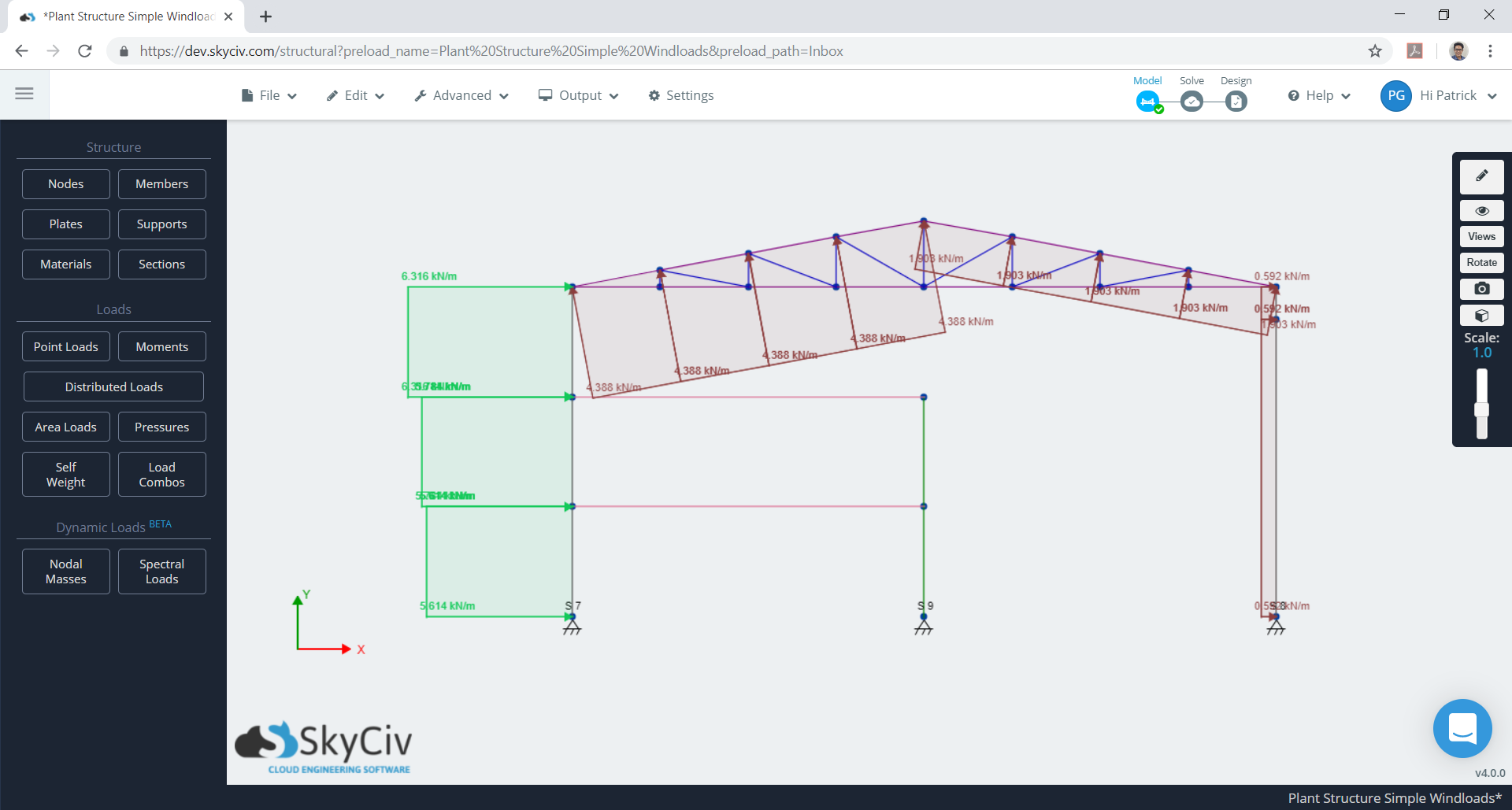
Zahl 24. Äquivalente Auslegungswinddrücke für einen Rahmen (Fall 2).
Diese Berechnungen können alle mit durchgeführt werden Windlas-Software von SkyCiv für ASCE 7-10, 7-16, IM 1991, NBBC 2015, AS 4055 und 1170. Benutzer können einen Standort eingeben, um Windgeschwindigkeiten und Topografiefaktoren abzurufen, Gebäudeparameter eingeben und Winddrücke erzeugen. Mit einem professionellen Konto, Benutzer können dies automatisch auf ein Strukturmodell anwenden und die Strukturanalyse in einer einzigen Software ausführen.
Andernfalls, Versuchen unsere SkyCiv Free Wind Tooloder Buche ein KOSTENLOSE DEMO um Unterstützung bei Ihren Engineering-Projekten für bestehende Benutzer zu erhalten
Statiker, Produktentwicklung
MS Bauingenieurwesen
Verweise:
- Gemeinsamer Technischer Ausschuss. (2011). AS / NZS 1170.2: 2011 Tragwerksplanung-Teil 2: Windaktionen. Australischer / neuseeländischer Standard (AS / NZS), Gemeinsamer Technischer Ausschuss BD-006, Australien / Neuseeland.


