Der Schwerpunkt oder Massenschwerpunkt von Balkenabschnitten ist für die Balkenanalyse nützlich, wenn das Trägheitsmoment für Berechnungen wie Scherung/Beschleunigung erforderlich ist.Biegespannung und Durchbiegungs. Dieser Artikel führt Sie durch einen einfachen Prozess zur Berechnung des Schwerpunkts und stellt Ihnen den SkyCiv Free Centroid Calculator vor.
So finden Sie Zentroid
Zunächst, Sie müssen wissen, wie man den Schwerpunkt findet. Balkenabschnitte bestehen normalerweise aus einer oder mehreren Formen. So finden Sie den Schwerpunkt eines gesamten Strahlquerschnittsbereichs, es muss zuerst in geeignete Segmente aufgeteilt werden. Danach, Die Fläche und der Schwerpunkt jedes einzelnen Segments müssen berücksichtigt werden, um den Schwerpunkt des gesamten Abschnitts zu ermitteln.
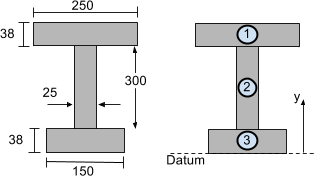
Betrachten wir den unten abgebildeten I-Trägerquerschnitt. Berechnung des vertikalen Schwerpunkts (in y-Richtung) es kann aufgeteilt werden in 3 Segmente unterteilt werden:
Jetzt müssen wir nur noch die Schwerpunktgleichung verwenden, um die Vertikale zu ermitteln (j) den Schwerpunkt einer Form mit mehreren Segmenten zu berechnen:

Wir nehmen das Datum oder die Referenzlinie von der Unterseite des Balkenabschnitts. Lassen Sie uns nun A findenich Andyich für jedes Segment des oben gezeigten I-Strahl-Abschnitts, so dass der vertikale oder y-Schwerpunkt gefunden werden kann.
[Mathematik]
\Text{Segment 1:}\\
\Start{ausrichten}
{Ein}_{1} &= 250 times38 = 9500 {\Text{ mm}}^{2}\\
{j}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \Text{ mm}\\\\
\Ende{ausrichten}
[Mathematik]
[Mathematik]
\Text{Segment 2:}\\
\Start{ausrichten}
{Ein}_{2} &= 300 times25 = 7500 {\Text{ mm}}^{2}\\
{j}_{2} &= 38 + \tfrac{300}{2} = 188 \Text{ mm}\\\\
\Ende{ausrichten}
[Mathematik]
[Mathematik]
\Text{Segment 3:}\\
\Start{ausrichten}
{Ein}_{3} &= 38 times150 = 5700 {\Text{ mm}}^{2}\\
{j}_{3} &= tfrac{38}{2} = 19 text{ mm}\\\\
\Ende{ausrichten}
[Mathematik]

Für den Fall, dass der Querschnitt aus zwei Materialien oder einem Verbundmaterial besteht, dann muss eines der Materialien mit dem modularen Verhältnis multipliziert werden, so dass der gesamte Abschnitt der Gleichung einheitlich wird.
[Mathematik]
n = frac{E_{1}}{E_{2}}
[Mathematik]
Normalerweise, E.1 ist der Elastizitätsmodul des nicht vorherrschenden Materials, und E.2 ist der Elastizitätsmodul des vorherrschenden Materials, Obwohl die bevorzugte Reihenfolge die Lösung des Schwerpunkts nicht beeinflusst. Anpassung für das zweite Material, die Schwerpunktgleichung wird wie folgt.
[Mathematik]
\Bar{j}= frac{\Summe{Ein}_{ich}{j}_{ich}+\Summe {n}{Ein}_{ich}{j}_{ich}}{\Summe{Ein}_{ich}+\Summe {n}{Ein}_{ich}}
[Mathematik]
Finden Sie den Schwerpunkt des Strahls mit SkyCiv
Es ist wichtig, den Schwerpunkt des Strahls zu ermitteln, die manuelle Berechnung kann jedoch zeitaufwändig sein. SkyCiv bietet eine Kostenloser Schwerpunktrechner das diesen Prozess für Sie automatisiert, hilft Ihnen, die Vertikale zu finden (j) und horizontal (x) Schwerpunkte von Balkenabschnitten einfach und genau ermitteln!
Dieses Tool ist eine kostenlose Version von SkyCiv Section Builder, eine umfassende Online-Schnittanalysesoftware zur geometrischen Analyse, Biegen, Schub- und Torsionsschnitteigenschaften sowie FEM- und Stahlbetonbemessung. Mit diesem Tool, Sie können benutzerdefinierte Abschnitte mithilfe vordefinierter Vorlagen erstellen oder Ihre eigenen Formen mit Punkten definieren, Linien, oder DXF-Importe aus CAD.
Um alle Funktionen zu erkunden SkyCiv Section Builder und erleben Sie die einfache Modellierung und Analyse Ihres Abschnitts, Melde dich heute kostenlos an!
Ähnliche Resourcen


