Allgemeine Beschreibung
SkyCiv verfügt über ein robustes und fortschrittliches Modul für die Konstruktion von Stahlbetonplatten. Um auf diese Funktion zuzugreifen, Sie müssen zunächst ein Modell auf SkyCiv S3D erstellt haben und dann das Modul zur automatischen Berechnung mit verschiedenen Baucodes wie ACI-318 aufrufen, Europäische und australische Standards, und so weiter. Der Hauptzweck des Moduls für die Plattenkonstruktion besteht darin, die Menge der Bewehrungsstäbe aus Stahl entlang der Platte bereitzustellen.
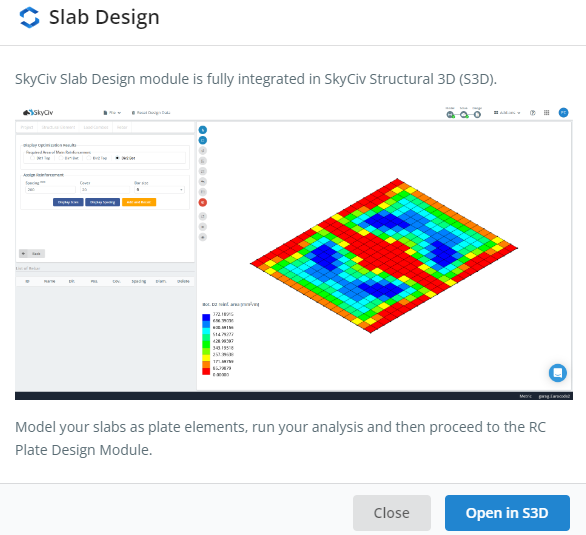
Zahl 1. SkyCiv Slab Design-Modul
Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!
Die SkyCiv-Dokumentation bietet hervorragende Inhalte, einschließlich Beispiele und Analysefälle, Sowohl zum Lernen, wenn Sie mit den Modulen noch nicht vertraut sind, als auch zum Vergleichen der Ergebnisse des Plattendesignmoduls mit Handberechnungen. Schauen Sie sich gerne unsere Designbeispiele an ACI-318, Eurocode, sowie AS3600.
Wir empfehlen Ihnen, diesen Artikel zu lesen, bevor Sie komplexe Plattensysteme eingehend analysieren. Hier, Sie erfahren, wie sich die Biegemomente je nach Plattengrundrissabmessungen unterscheiden. Es gibt zwei Studienfälle, Einweg- und Zweiwegplatten. So, Fangen wir an zu lesen!
Einseitiges versus zweiseitiges Plattenverhalten
Betrachten wir das Plattenbeispiel im folgenden Bild, wo an jeder Plattenkante eine Stütze vorhanden ist, und wir stellen fest, dass sich dies wie eine Zwei-Wege-Platte verhält, das ist, ein Biegemoment in den beiden Hauptgrundrissrichtungen aufweist.
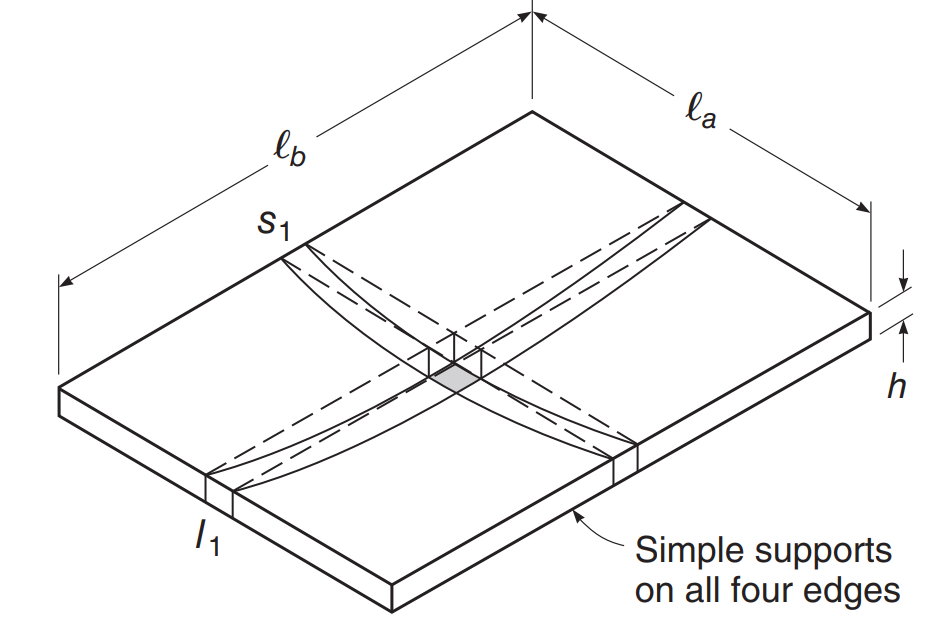
Zahl 2. Einfaches Beispiel einer bidirektionalen Platte zum Biegen. (David Darwin, Charles W. Dolan, Arthur H. Nilson, “Entwurf von Betonkonstruktionen,” Fünfzehnte Auflage, McGraw-Hill-Ausbildung)
Wir können die vertikale Verschiebung definieren als (\(l_a < Pfund \)):
\(\Delta_a = \frac{{5}{w_a}{l_a^4}}{384{E.}{I}}\)
\(\Delta_b = \frac{{5}{w_b}{l_b^4}}{384{E.}{I}}\)
Da es sich bei der Platte um ein durchgehendes System handelt, beide vertikalen Auslenkungen haben den gleichen Wert. Wir können die Gleichungen vergleichen, um eine Beziehung zwischen der von jeder Richtung getragenen Last als Funktion der Planabmessungen auszudrücken.
\(\Delta_a = \Delta_b \to \frac{{5}{w_a}{l_a^4}}{384{E.}{I}} = frac{{5}{w_b}{l_b^4}}{384{E.}{I}}\)
\(\frac{w_a}{w_b} = {(\frac{Pfund}{l_a}})^4 \)
Alle Stahlbetonreferenzen für die Plattenbemessung teilen sich in eine Richtung und zwei Richtungen auf, wenn der Quotient aus ist \(\frac{Pfund}{l_a}\) ist größer oder kleiner als ein Wert von 2, beziehungsweise.
Unter Verwendung der obigen Gleichungen, Wann \(\frac{Pfund}{l_a}=2\), Die in der kurzen Richtung getragene Last ist gleich \(w_a = {16}{w_b}\) und wann der Wert ist \(\frac{Pfund}{l_a}=1), Die Last wird in beide Richtungen gleichmäßig verteilt \(w_a ={w_b}\).
Einwegplattenmomente
So, Wir können das sehen, wenn der Quotient der Dimensionen größer ist als 2, praktisch, Alle Lasten und Biegemomente werden nur in der kurzen Richtung konzentriert. In diesem Fall handelt es sich um das Einwegplattenverhalten, und das maximale Biegemoment kann als einfach gelagerter Träger mit einheitlicher Breite erhalten werden.
\(M_{max,1,D.}= frac{{w_a}{1 m}{l_a^2}}{8}\)
Zwei-Wege-Plattenmomente
Die Lösung des Falles der Zweiwegeplatte ist ein komplexes und anspruchsvolles Problem der Strukturmechanik. In der folgenden Abbildung können Sie sehen, dass die allgemeine Analyse aus einer Platte mit den gesamten Kräften und Momenten in jede Richtung besteht.
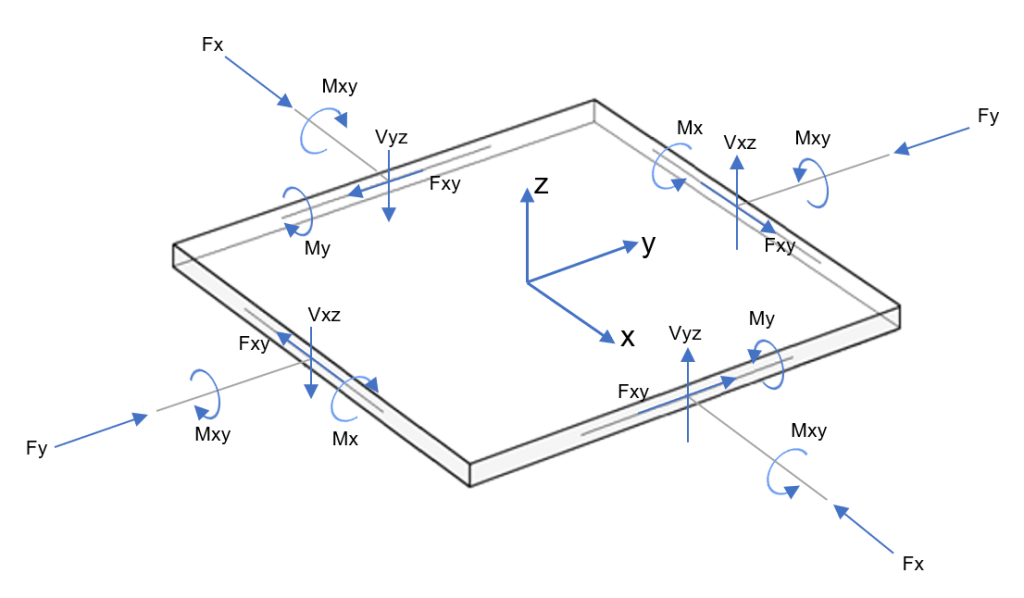
Zahl 3. Aktionen auf Plattenelement (Biege- und Torsionsmomente; Normal- und Scherkräfte)
Diese Schwierigkeit ergibt sich daraus, dass es sich bei dem eigentlich zu lösenden Problem um eine partielle Differentialgleichung vierter Ordnung handelt, die die Biegung in zwei Richtungen beinhaltet. Die Form dieser Gleichung ist:
\(\frac{\teilweise^4{w}}{{\teilweise}{x^4}} + {2}\frac{{\teilweise^4}{w}}{{{\teilweise}{x^2}}{{\teilweise}{y^2}}}+\frac{\teilweise^4{w}}{{\teilweise}{x^4}}-\frac{f_z}{D.} = 0\)
Wo die Plattensteifigkeit (Nutzung der elastischen mechanischen und geometrischen Eigenschaften) ist \(D=\frac{{E.}{t^3}}{{12}{(1-\nein^2)}}\).
Die analytische Lösung dieser Gleichung ist nur für einfache Stützbedingungen verfügbar. Die einzige Möglichkeit, eine mögliche Lösung für praktische und tatsächliche Live-Fälle zu erhalten, sind numerische Methoden wie die Finite-Elemente-Methode.
SkyCiv verwendet diesen Ansatz zur Lösung der Plattenanalyse. Auf den folgenden Links, Sie haben Zugriff auf Tutorials, um mehr über die Eigenschaften der SkyCiv-Plattform zu erfahren: Plattendesign in S3D sowie So modellieren Sie Platten? .
Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!

