Eine exemplarische Vorgehensweise für die Berechnungen zum Entwurf eines isolierten Fundaments (ACI 318-14)

Das Fundament ist ein wesentliches Bausystem, das Stützen- und Wandkräfte auf den tragenden Boden überträgt. Abhängig von den Bodeneigenschaften und den Gebäudelasten kann sich der Ingenieur für ein flaches oder tiefes Fundamentsystem entscheiden.

SkyCiv FoundationDesign-Modul Beinhaltet die Analyse und Gestaltung isolierter Fundamente gemäß dem amerikanischen Code ACI318-14.

 

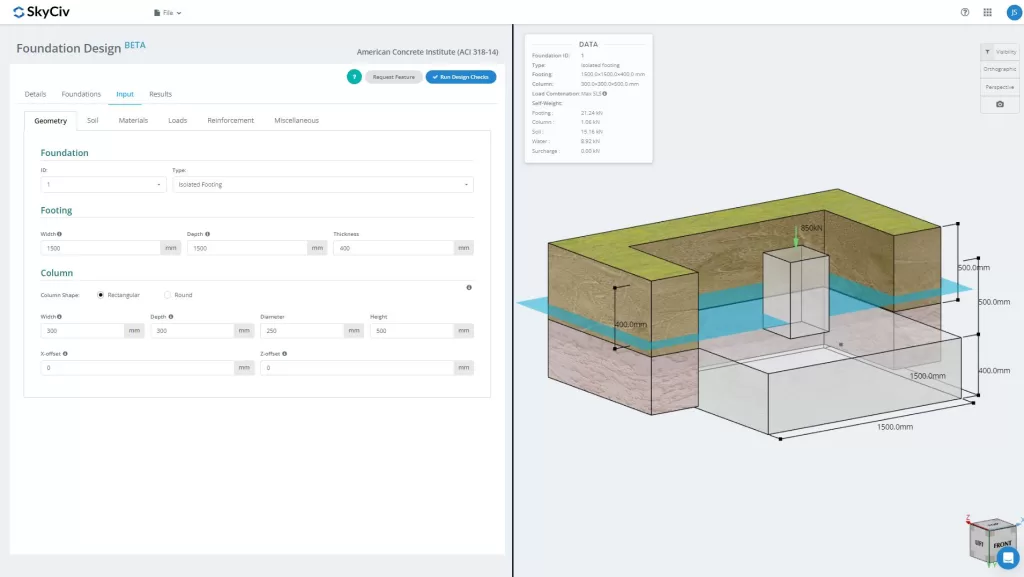
Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Mit unserem Tool können Benutzer Foundation Design-Berechnungen durchführen, ohne es herunterladen oder installieren zu müssen!

Foundation Design Calculator

 

Eine Schritt-für-Schritt-Anleitung zum Entwerfen eines isolierten Fundaments

Abmessungsanforderungen

Zur Bestimmung der Abmessungen eines isolierten Fundaments, Service oder nicht faktorisierte Lasten, wie tot (D.), Verkehrslast (L.), Wind (W.), Seismisch (E.), usw. werden mit Lastkombinationen angewendet, wie von ACI . definiert 318-14. Welche Lastkombination vorherrscht, wird als Bemessungslast betrachtet, und wird mit dem zulässigen Bodendruck verglichen, wie in Gleichung . gezeigt 1, wie empfohlen in Sektion 13.2.6 von ACI 318-14.

\(\Text{q}_{\Text{ein}} = frac{\Text{P.}_{\Text{n}}}{\Text{Ein}} \rechter Pfeil \) Gleichung 1

q_ein = Zulässiger Bodendruck
P._n = Unberücksichtigte Auslegungslast
A = Fundamentfläche

 

Die Fundamentabmessungen können zunächst durch Lösen der Fundamentfläche abgeschätzt werden (Ein) unter Verwendung von Gleichung 1.

 

\(\Text{Ein} = frac{\Text{P.}_{\Text{n}}}{\Text{q}_{\Text{ein}}} \rechter Pfeil \) Gleichung 1a

 

Einwegschere

Der Grenzzustand der Einwegscherung, auch als Balkenscherung bekannt, erkennt an, dass das Fundament bei Scherung ähnlich wie bei einem breiten Balken entlang einer kritischen Scherungsebene in einiger Entfernung versagen kann “d” von der Vorderseite der Säule (Abbildung 1),

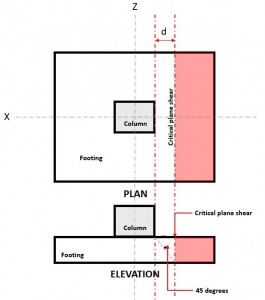
Abbildung 1. Kritische Ebenenschere der Einwegschere

Mit der Einweg Scheren Nachfrage oder V _u wird unter der Annahme berechnet, dass das Fundament von der Säule weg auskragt, wo in der Abbildung der rote Bereich angegeben ist 1, folgende Sektion 8.5.3.1.1.

Mit der Einweg-Scherkapazität oder V_c wird als ultimative Scherfestigkeit definiert und mithilfe der Gleichung berechnet 2 pro Sektion 22.5.5.1.

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 2 \sqrt{\Text{F'}_{\Text{c}}} \mal text{b}_{\Text{w}} \mal text{d} \rechter Pfeil \) Gleichung 2 ( Sektion 22.5.5.1, Kaiserliche)

oder

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 0.17 \sqrt{\Text{F'}_{\Text{c}}} \mal text{b}_{\Text{w}} \mal text{d} \rechter Pfeil \) Gleichung 2 (Sektion 22.5.5.1, Metrisch)

φ_Schub- = Scherbemessungsfaktor
f’_c = Angegebene Betonfestigkeit, (psi, MPa)
b_w = Breite des Fundaments, (im, mm)
d = Abstand von der extremen Druckfaser zum Schwerpunkt der Längszugbewehrung, (im, mm)

Scherbedarf und Scherkapazität müssen die folgende Gleichung erfüllen, um die Konstruktionsanforderungen von ACI . zu erfüllen 318-14:

\(\Text{V }_{\Text{u}} \leq phitext{V }_{\Text{c}} \rechter Pfeil \) Gleichung 3 (ACI-Gl. 7.5.1.1(b))

 

Designmodul der SkyCiv Foundation, in Übereinstimmung mit der Gleichung 3, berechnet das Einweg-Schernutzenverhältnis (Gleichung 4) indem man den Scherbedarf über die Scherkapazität nimmt.

\( \Text{Nutzenverhältnis} = frac{\Text{Scherbedarf}}{\Text{Scherkapazität}} \rechter Pfeil \) Gleichung 4

 

Zwei-Wege-Schere

Der Grenzzustand der bidirektionalen Scherung, auch als Durchstanzschere bekannt, erweitert seinen kritischen Abschnitt auf eine Distanz “d/2” von der Stirnseite der Säule und um den Umfang der Säule (Abbildung 2).

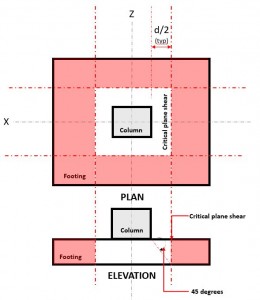
Abbildung 2. Kritische Scherebene der Zwei-Wege-Schere

Mit der Zwei WegeNachfrage hören oder V _u tritt an der kritischen Scherebene auf, befindet sich in einer Entfernung von “d/2” bei dem die (rot) schraffierter Bereich, in Abbildung angegeben 2, folgende Sektion 22.6.4.

Mit der Scherkapazität oder V_c wird durch den kleinsten Wert bestimmt, der mithilfe von Gleichungen berechnet wird 5, 6, und 7 pro Sektion 22.6.5.2

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 4 \mal lambda times sqrt{\Text{F'}_{\Text{c}}} \rechter Pfeil \) Gleichung 5 (Sektion 22.6.5.2(ein) Kaiserliche)

\(\phitext{V }_{\Text{c}} = links ( 2 + \frac{4}{\Beta } \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 6 (Sektion 22.6.5.2(b) Kaiserliche)

\(\phitext{V }_{\Text{c}} = left ( 2 + \frac{\alpha_{s} \mal d }{b{Das}} \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 7 (Sektion 22.6.5.2(c) Kaiserliche)

oder

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 0.33 \mal lambda times sqrt{\Text{F'}_{\Text{c}}} \rechter Pfeil \) Gleichung 5 (Sektion 22.6.5.2(ein) Metrisch)

\(\phitext{V }_{\Text{c}} = 0.17 \mal links ( 1 + \frac{2}{\Beta } \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 6 (Sektion 22.6.5.2(b) Metrisch)

\(\phitext{V }_{\Text{c}} = 0.0083 \mal links ( 2 + \frac{\alpha_{s} \mal d }{b{Das}} \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 7 (Sektion 22.6.5.2(c) Metrisch)

Hinweis: β ist das Verhältnis der langen Seite zur kurzen Seite der Säule, Einzellast, oder Reaktionsfläche und α_s wird gegeben von 22.6.5.3

λ = Modifikationsfaktor, um die verringerten mechanischen Eigenschaften von Leichtbeton im Vergleich zu Normalbeton gleicher Druckfestigkeit widerzuspiegeln
f’_c = Angegebene Betondruckfestigkeit (psi, MPa)
d = Abstand von der extremen Druckfaser zum Schwerpunkt der Längszugbewehrung, (im, mm)

 

Scherbedarf und Scherkapazität müssen die folgende Gleichung erfüllen, um die Konstruktionsanforderungen von ACI . zu erfüllen 318-14:

\(\Text{V }_{\Text{u}} \leq phitext{V }_{\Text{c}} \rechter Pfeil \) Gleichung 8 (Sektion 7.5.1.1(b))

 

Designmodul der SkyCiv Foundation, in Übereinstimmung mit der Gleichung 8, berechnet das Zwei-Wege-Scher-Nutzverhältnis (Gleichung 9) indem man den Scherbedarf über die Scherkapazität nimmt.

\( \Text{Nutzenverhältnis} = frac{\Text{Scherbedarf}}{\Text{Scherkapazität}} \rechter Pfeil \) Gleichung 9

Biegung

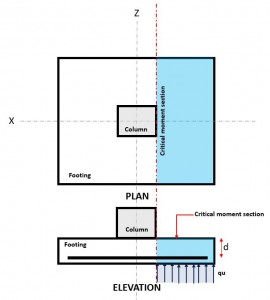
Abbildung 3. Kritischer Biegeabschnitt

Mit der Biege Grenzzustand tritt auf der kritische Biegeabschnitt, befindet sich an der Stirnseite der Stütze oben auf dem Fundament (Abbildung 3).

Mit der Biegebedarf oder M._u befindet sich in der Critical Flexure Section (blauer Lukenbereich) in Abbildung angegeben 3, und wird mit Gleichung . berechnet 10.

\( \Text{M.}_{u} = text{q}_{u} \mal links ( \frac{l_{x}}{2} – \frac{c_{x}}{2} \richtig ) \mal l_{mit} \mal links ( \frac{\frac{l_{x}}{2} – \frac{c_{x}}{2} }{2} \richtig ) \rechter Pfeil \) Gleichung 10

q_u = faktorisierter Bodendruck, (ksf, kPa)
l_x = Fundamentmaß entlang der x-Achse (im, mm)
l_mit = Fundamentmaß entlang der z-Achse (im, mm)
c_x = Spaltenabmessung entlang der x-Achse (im, mm)

Mit der Biegekapazität oder Mn wird mit Gleichung berechnet 11.

\( \phitext{M.}_{n} = phi_{\Text{Biegung}} \mal A_{s} \mal f_{j} \mal links( d – \frac{ein}{2} \richtig) \rechter Pfeil \) Gleichung 11

ϕ = Biegebemessungsfaktor
l_x = Fundamentmaß parallel zur x-Achse (im , mm)
l_mit = Fundamentmaß parallel zur z-Achse (im , mm)
d = Abstand von der Extremdruckfaser zum Schwerpunkt der Längszugbewehrung (im , mm)
Ein_s = Verstärkungsbereich (im² , mm²)
a = Tiefe des äquivalenten rechteckigen Spannungsblocks (im , mm)
fy = Bewehrungsstärke, (KSI, MPa)

 

Zusätzliche Überprüfungen

Andere Überprüfungen, die im Code nicht erwähnt werden, einschließlich Bodendruckprüfungen, erheben, und andere Stabilitätsprüfungen werden ebenfalls überprüft.

Bodendruck

Die Bestimmung des Sockeldrucks bzw. der Wechselwirkung zwischen Boden und Fundament beruht in erster Linie auf den Abmessungen des Fundaments und der daraus resultierenden Exzentrizität der aufgebrachten Lasten. Je nach Positionierung ergibt sich daraus eine Exzentrizität, Der Grunddruck kann zu einer vollständigen oder teilweisen Kompression des Fundaments führen. Mit dieser Bewertung können wir bestätigen, ob der darunter liegende Boden die gesamten vom Fundament übertragenen Lasten tragen kann.

Eine ausführliche Anleitung zur manuellen Berechnung des Bodendrucks finden Sie hier, Bitte beachten Sie diesen Link: Druckverteilung unter einem rechteckigen Betonfundament

Das Nutzenverhältnis wird durch Vergleich des maximalen Bodendrucks ermittelt (Zustand der Gebrauchstauglichkeit) mit der zulässigen Bruttotragfähigkeit des Bodens:

 

\( \Text{Nutzenverhältnis} = frac{\Text{Max. Bodendruck}}{\Text{Bruttozulässige Bodentragfähigkeit}} \rechter Pfeil \) Gleichung 14

Erheben

Überprüft die maßgebende Axiallast, die auf das Fundament wirkt. Summiert alle vertikalen Lasten einschließlich der Benutzerlast und des Eigengewichts der Säule, Bodenplatte, Boden, und Auftriebskraft. Wenn die Säule eine nach oben gerichtete Kraft erfährt, Die angegebenen Eigengewichte müssen die Auftriebskraft ausgleichen; Andernfalls, Bei der Konstruktion besteht die Gefahr, dass sie aufgrund von Instabilität versagt.

Umkippen

Das Umkippen des Fundaments wird überprüft, indem alle Momente um einen Punkt im Fundament einschließlich aller auf ihn einwirkenden Kräfte summiert werden. Zur Überprüfung des maßgebenden Kippmoments müssen alle Gebrauchslastkombinationen berücksichtigt werden. Üblicherweise, ein Sicherheitsfaktor von 1.5-2 wird verwendet, um zu bewerten, ob das Fundament die Kippprüfung besteht.

Gleiten

Zur Prüfung auf Gleiten, Die Summe der nach rechts gerichteten horizontalen Widerstandslasten wird durch die Summe der nach links gerichteten Lasten dividiert.

• Beispiel für die Berechnung des Kippmoments:
  • Horizontalkraft aufgrund von Reibung zwischen der Gründungsbasis und dem Unterbauboden
  • Passiver Bodendruck (falls enthalten)
• Rutschende Lasten:
  • Die horizontale Komponente des aktiven Bodendrucks
  • Die horizontale Komponente des resultierenden Drucks des Aufschlags

Allgemein, ein Mindestsicherheitsfaktor von 1.5 wird eingesetzt. Wenn keine horizontale Kraft auf den Untergrund einwirkt, Eine Prüfung auf Gleiten ist nicht erforderlich.

Designmodul der SkyCiv Foundation

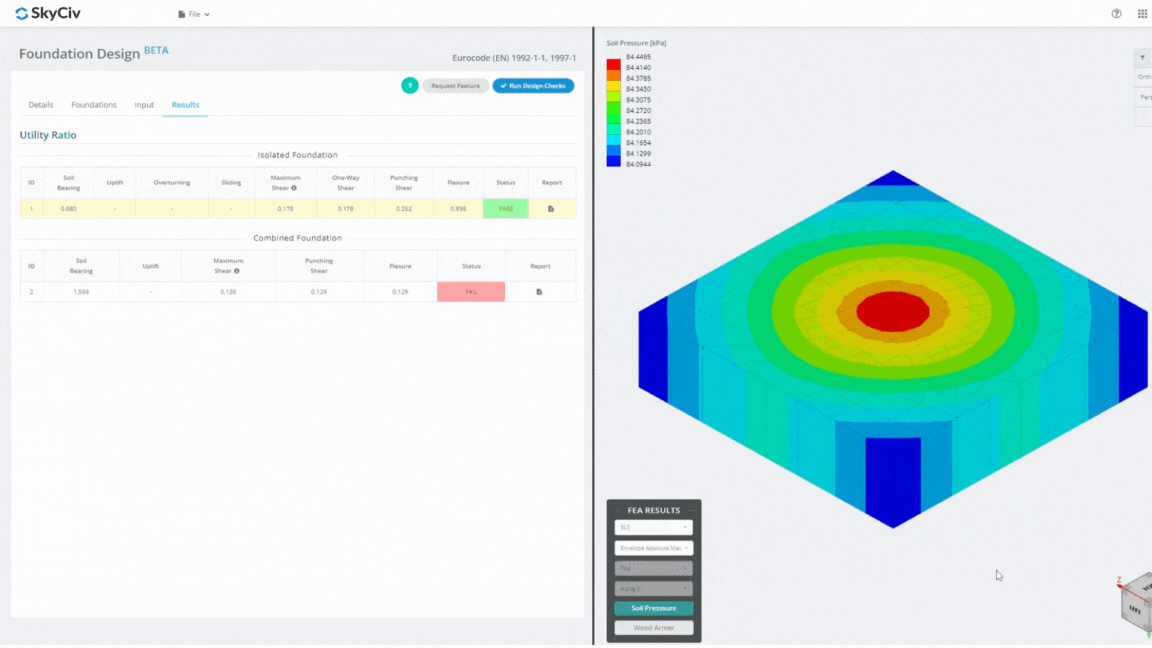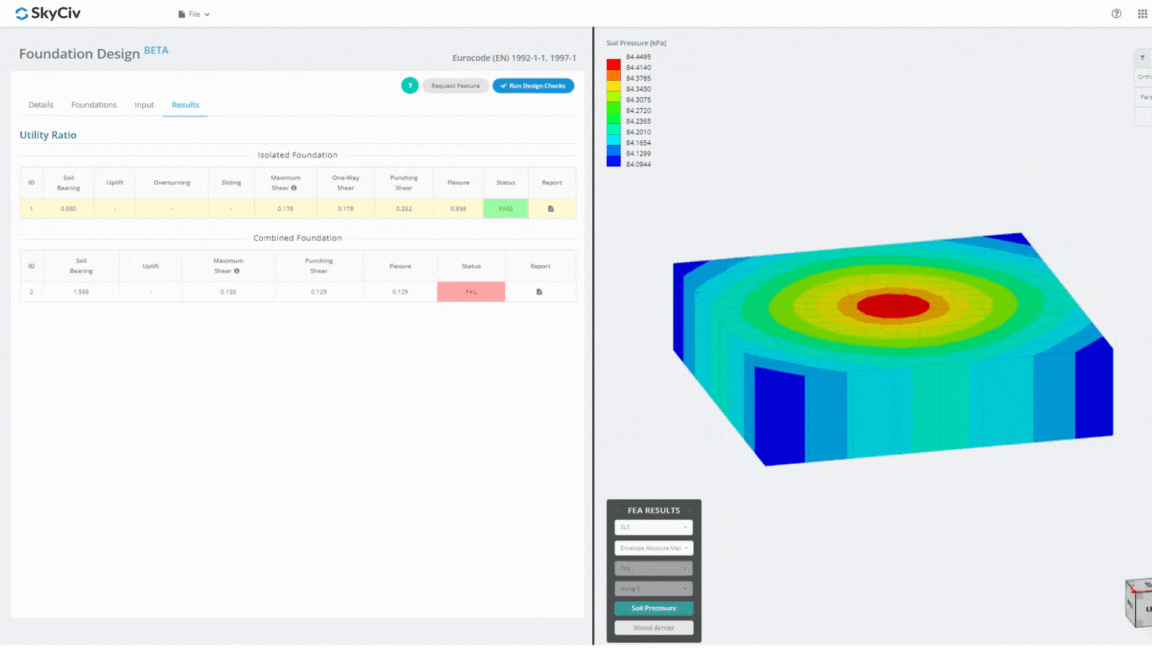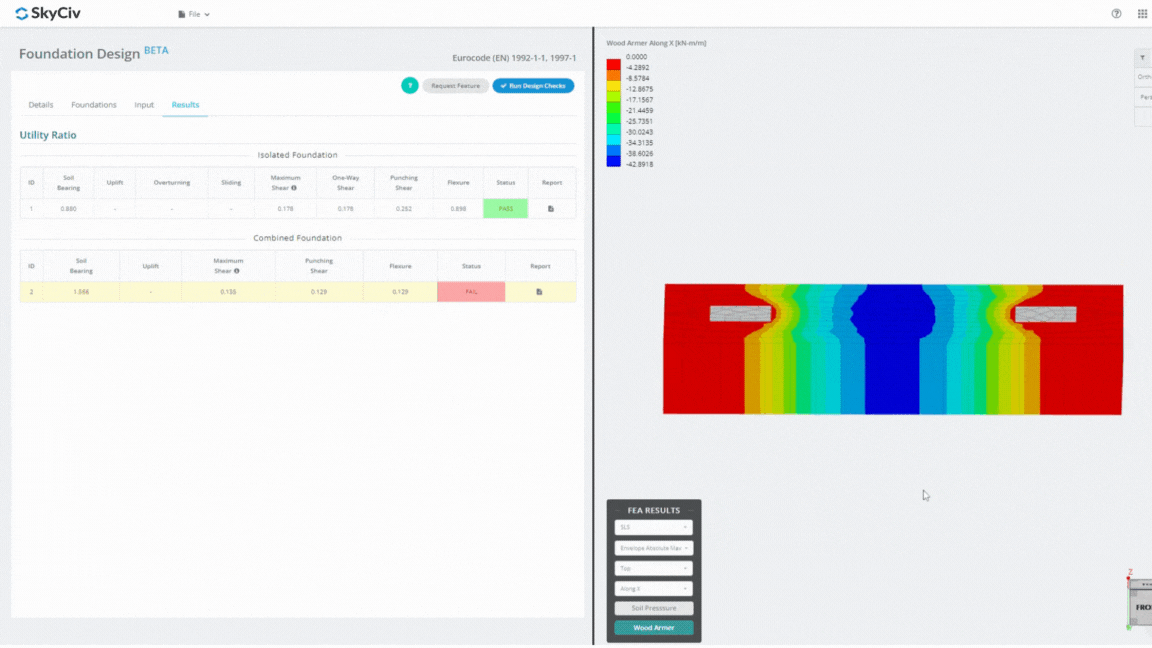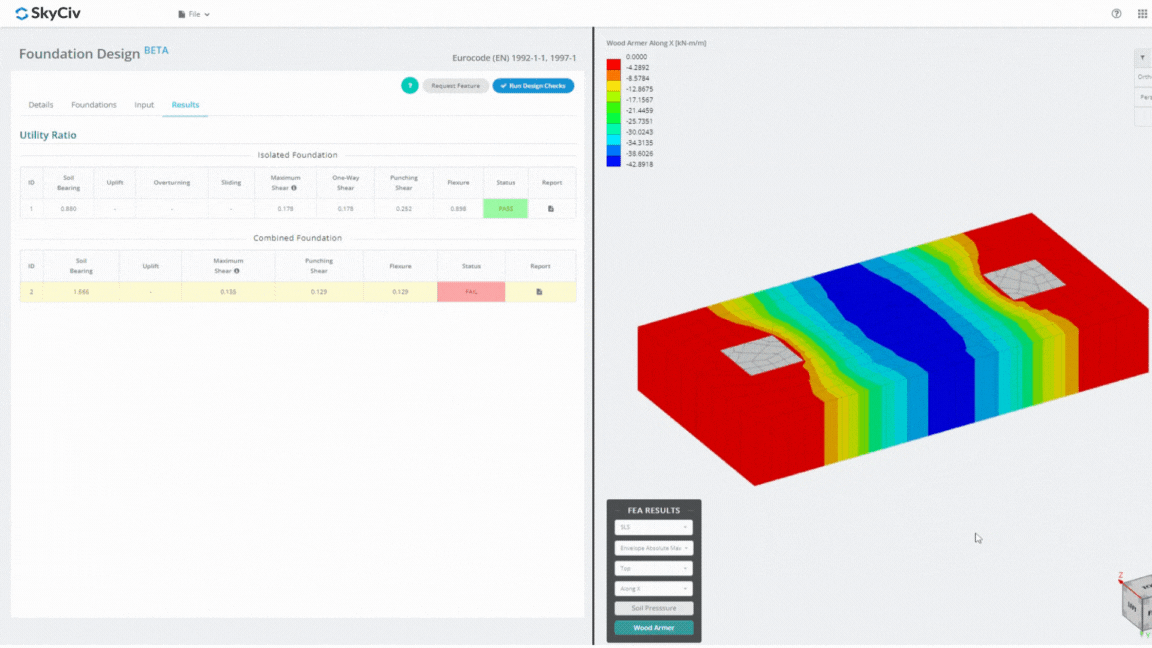
Das Foundation Design Module ist ein leistungsstarkes Tool, das in die Finite-Elemente-Analyse integriert ist (HÄSSLICH), ist in der Lage, gründliche Bodendruck- und Holzarmierungsanalysen für detaillierte Biegeprüfungen durchzuführen. Es führt alle von ACI vorgeschriebenen Strukturprüfungen durch 318 und weitere oben genannte Nachweise und stellt diese in einem umfassenden Bericht dar.

Beginnen Sie mit der SkyCiv Foundation heute!

Starte den Foundation Design und versuchen Sie es noch heute! Der Einstieg ist einfach, aber wenn Sie weitere Hilfe benötigen, dann besuchen Sie unbedingt unsere Dokumentation oder nehmen Sie Kontakt mit uns auf!

Kein SkyCiv-Benutzer? Melden Sie sich für a . an kostenlos 14 Tagesversuch um loszulegen!

Verweise

1. Bauvorschriften für Konstruktionsbeton (ACI 318-14) Kommentar zu baurechtlichen Anforderungen an tragenden Beton (ACI 318R-14). Amerikanisches Betoninstitut, 2014.
2. McCormac, Jack C., und Russell H. Braun. Bemessung von Stahlbeton ACI 318-11 Code-Edition. Wiley, 2014.
3. Taylor, Andreas, et al. The Reinforced Concrete Design Handbook: ein Begleiter zu ACI-318-14. Amerikanisches Betoninstitut, 2015.