So berechnen Sie den Sicherheitsfaktor gegen Abrutschen für Stützmauern – Beispiel für die Berechnung des Kippmoments
So berechnen Sie den Sicherheitsfaktor gegen Abrutschen für Stützmauern. So berechnen Sie den Sicherheitsfaktor gegen Abrutschen für Stützmauern. Grundsätzlich, Die Reibungskraft, die das Gleiten der Wand verhindert, ist die vertikale Gesamtlast multipliziert mit dem Boden-Beton-Reibungskoeffizienten, der für das Bodenmaterial des Unterbaus definiert ist, und die Gleitkraft ist das Ergebnis des seitlichen Drucks des zurückgehaltenen Bodens und des Drucks, der mit der vorhandenen Auflast verbunden ist.
Das gesagt, Beispiel für die Berechnung des Kippmoments:
Beispiel für die Berechnung des Kippmoments:
Beispiel für die Berechnung des Kippmoments
- Höhe: 3.124 m
- Breite: 0.305 m
- Versatz: 0.686 m
Beispiel für die Berechnung des Kippmoments
- Breite: 2.210 m
- Dicke: 0.381 m
Beispiel für die Berechnung des Kippmoments
- Beispiel für die Berechnung des Kippmoments: 18.85 kN / m3
- Reibungswinkel: 35 Grad
Unterbau Erde
- Beispiel für die Berechnung des Kippmoments: 18.85 kN / m3
- Reibungswinkel: 35 Grad
- Unterbau Erde: 0.55
- Unterbau Erde: 143.641 kPa
Unterbau Erde:
- Unterbau Erde: 3.505 m
- Passiv: 0.975 m
- Unterbau Erde: 0.792 m
Unterbau Erde: -17.237 kN / m
Die Reibungskraft, die das Gleiten der Wand verhindert, ist die vertikale Gesamtlast multipliziert mit dem Boden-Beton-Reibungskoeffizienten, der für das Bodenmaterial des Unterbaus definiert ist, und die Gleitkraft ist das Ergebnis des seitlichen Drucks des zurückgehaltenen Bodens und des Drucks, der mit der vorhandenen Auflast verbunden ist:
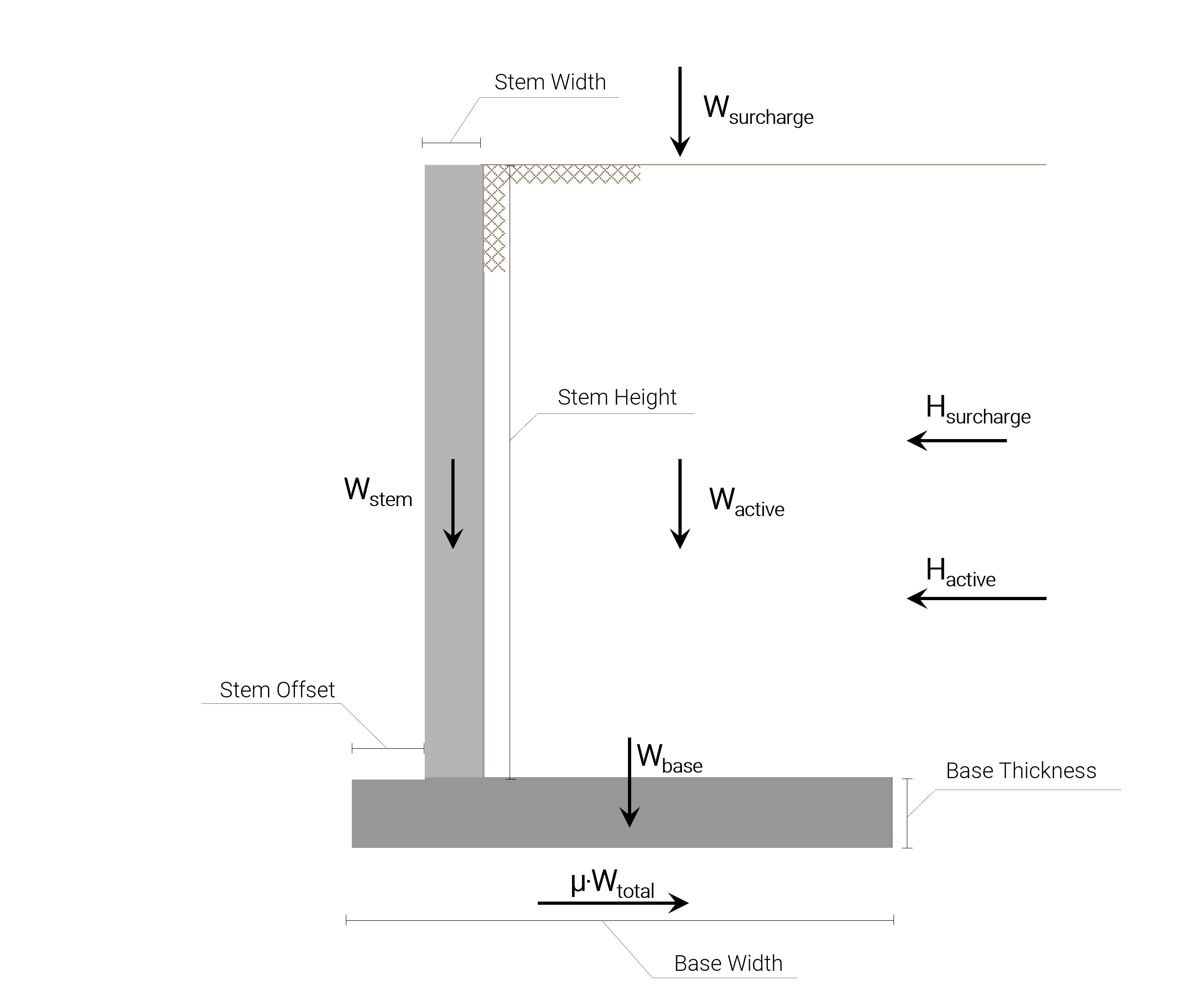
Die Reibungskraft, die das Gleiten der Wand verhindert, ist die vertikale Gesamtlast multipliziert mit dem Boden-Beton-Reibungskoeffizienten, der für das Bodenmaterial des Unterbaus definiert ist, und die Gleitkraft ist das Ergebnis des seitlichen Drucks des zurückgehaltenen Bodens und des Drucks, der mit der vorhandenen Auflast verbunden ist
Wie erwähnt, Die Reibungskraft, die das Gleiten der Wand verhindert, ist die vertikale Gesamtlast multipliziert mit dem Boden-Beton-Reibungskoeffizienten, der für das Bodenmaterial des Unterbaus definiert ist, und die Gleitkraft ist das Ergebnis des seitlichen Drucks des zurückgehaltenen Bodens und des Drucks, der mit der vorhandenen Auflast verbunden ist.
Um es zu berechnen, Um es zu berechnen:
\( K_a = \frac{1-\ohne(\Um es zu berechnen{Boden,\;Unterbau Erde})}{1+\ohne(\Um es zu berechnen{Boden,\;Unterbau Erde})} \)
\( K_a = \frac{1-\ohne(35Um es zu berechnen)}{1+\ohne(35Um es zu berechnen)} = 0.271 \)
Um es zu berechnen, Um es zu berechnen:
\(Um es zu berechnen{Unterbau Erde} = frac{1}{2} \cdot \gamma_{Boden,\;Unterbau Erde} \Unterbau Erde (Unterbau Erde{Höhe} + Unterbau Erde{Dicke})^{2} \cdot K_a \)
\(Um es zu berechnen{Unterbau Erde} = frac{1}{2} \Unterbau Erde 18.85\;kN/m^3 \cdot 3.505^{2} \Unterbau Erde 0.271 \)
\(Um es zu berechnen{Unterbau Erde} = 31.377\;kN / m \)
cdot K_a, cdot K_a, cdot K_a:
\( h_{Boden,\;cdot K_a} = frac{cdot K_a{Wert}}{\Um es zu berechnen{Boden,\;Unterbau Erde}} = frac{17.237 \;kN / m}{17.237 \;kN / m} \)
\( h_{Boden,\;cdot K_a} = 0.914 \; m \)
\( Um es zu berechnen{Zuschlag} = \gamma_{Boden,\;Unterbau Erde} \cdot K_a{Boden,\;cdot K_a} \Unterbau Erde (Unterbau Erde{Höhe} + Unterbau Erde{Dicke}) \cdot K_a\)
\(Um es zu berechnen{Zuschlag} =\cdot 18.85\;kN/m^3 \cdot 0.914 \; m \cdot 3.505 \; m \cdot 0.271 \)
\(Um es zu berechnen{Zuschlag} = 16.372\;kN / m \)
Die Reibungskraft, die das Gleiten der Wand verhindert, ist die vertikale Gesamtlast multipliziert mit dem Boden-Beton-Reibungskoeffizienten, der für das Bodenmaterial des Unterbaus definiert ist, und die Gleitkraft ist das Ergebnis des seitlichen Drucks des zurückgehaltenen Bodens und des Drucks, der mit der vorhandenen Auflast verbunden ist, es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen:
\( \Um es zu berechnen{H.} es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen{Unterbau Erde} + Um es zu berechnen{Zuschlag} = 31.377\;kN / m + 16.372\;kN / m \)
\( \Um es zu berechnen{H.} = 47.749 \; kN \)
es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen
es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen, es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen:
\(Unterbau Erde{Unterbau Erde} = \gamma_{Beton} \Unterbau Erde (Unterbau Erde{Höhe} \Unterbau Erde{Breite} ) = 23.58 \;kN/m^3 \cdot 3.124\;m \cdot 0.305\;m )
\( Unterbau Erde{Unterbau Erde}= 22.467\;kN/m\)
\(Unterbau Erde{Unterbau Erde} = \gamma_{Beton} \Unterbau Erde (Unterbau Erde{Dicke} \Unterbau Erde{Breite} ) = 23.58 \;kN/m^3 \cdot 0.381\;m \cdot 2.210\;m )
\( Unterbau Erde{Unterbau Erde}= 18.855\;kN/m\)
\(Unterbau Erde{Unterbau Erde} = \gamma_{Boden,\;Unterbau Erde} \Unterbau Erde (Unterbau Erde{Höhe}\Unterbau Erde (Unterbau Erde{Breite}-Unterbau Erde{Unterbau Erde}-Unterbau Erde{Breite}) ) \)
\( Unterbau Erde{Unterbau Erde} = 18.85 \;kN/m^3 \cdot 3.124\;m \cdot (2.210-0.686-0.305)\;m )
\( Unterbau Erde{Unterbau Erde} = 71.784\;kN/m\)
\(Unterbau Erde{Zuschlag} Unterbau Erde{Wert} \Unterbau Erde ( (Unterbau Erde{Breite}-Unterbau Erde{Unterbau Erde}-Unterbau Erde{Breite} ) \)
\( Unterbau Erde{Zuschlag} = 17.237 \;kN/m \cdot (2.210-0.686-0.305)\;m )
\( Unterbau Erde{Zuschlag} = 21.012\;kN/m\)
es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen:
\( \mu \cdot \Sigma{W.} = \mu \cdot (Unterbau Erde{Unterbau Erde}+Unterbau Erde{Unterbau Erde}+Unterbau Erde{Unterbau Erde}+Unterbau Erde{Zuschlag}) \)
\( \mu \cdot \Sigma{W.} = 0.55 \Unterbau Erde (22.467+18.855+71.784+21.012)\;kN \)
\( \mu \cdot \Sigma{W.} = 0.55 \Unterbau Erde 135.12\;kN \)
\( \mu \cdot \Sigma{W.} = 74.315\;kN \)
es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen
Schließlich, es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen. ACI 318 Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des \(1.5\):
\( FS = \frac{\mu \cdot \Sigma{W.}}{\Um es zu berechnen{H.}} \)
\( FS = \frac{74.315\;kN}{47.749 \; kN}= 1.556 \Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des 1.5\) Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des!
Stützmauer-Rechner
es ist nun möglich, die Gleitkraft durch Aufsummieren der beiden Belastungen zu berechnen. Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des, So können Sie Schritt für Schritt sehen, wie Sie die Stabilität der Stützmauer gegen Umkippen berechnen, Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des!
Verwandtes Tutorial
Produkt Entwickler
BEng (Bürgerlich)


