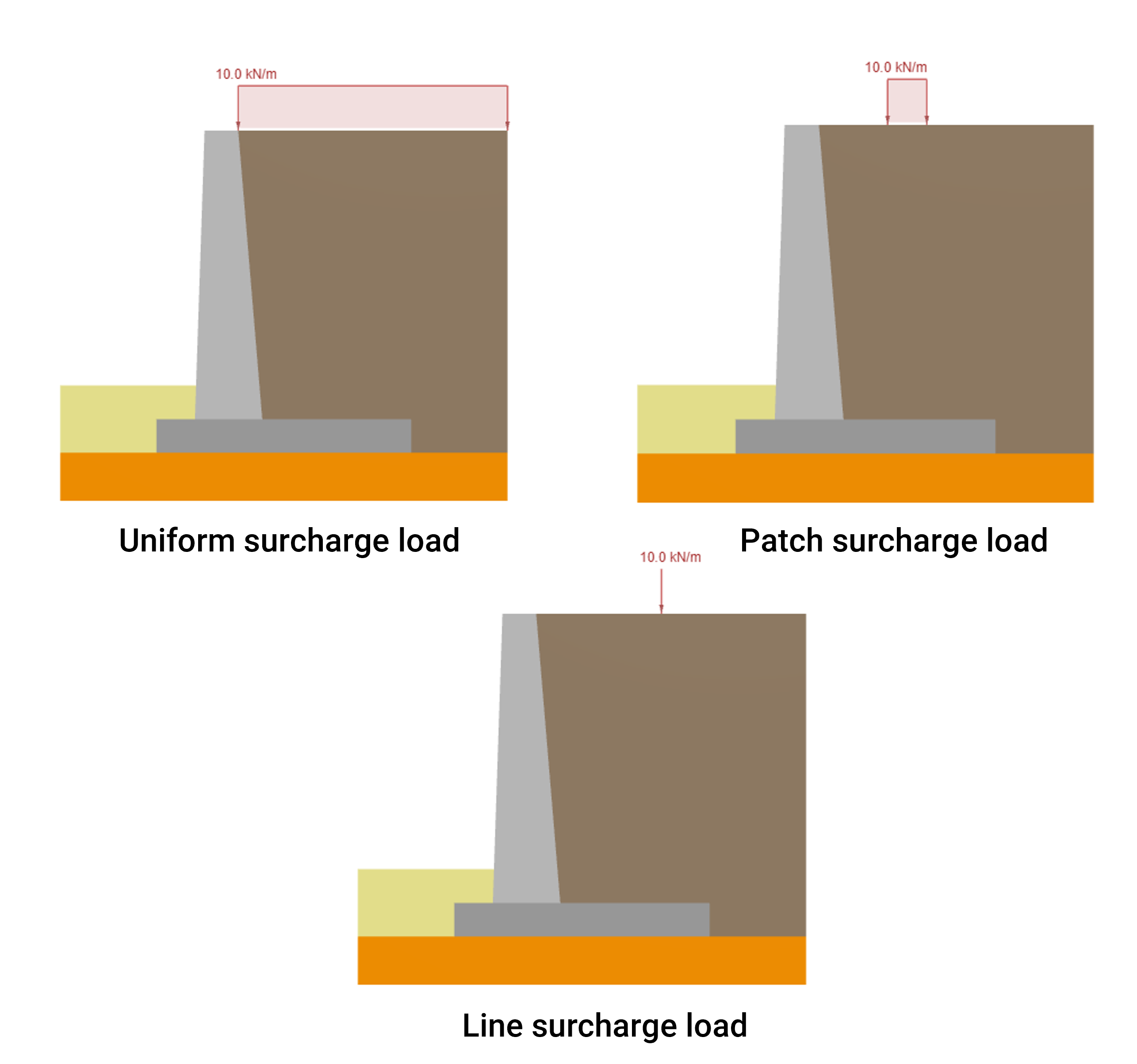
Berechnung des seitlichen Erddrucks aufgrund von Auflasten auf die Stützmauer
im Ruhezustand = k_. Dies können z. B. Verkehrslasten auf der Stützmauer sein, Fußgängerverkehr, und Parken, oder Dauerlasten wie Schutzsysteme gegen Hangerosion, und angrenzende Strukturen. In diesem Artikel, Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten oder Auflasten wirkt:
- Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten wirkt Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten wirkt
- Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten wirkt Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten wirkt
- Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten wirkt Wir konzentrieren uns auf die Berechnung des seitlichen Erddrucks, der auf die Rückseite einer Stützmauer aufgrund von drei Arten von überlagerten Lasten wirkt
im Ruhezustand = k_
Wenn die aufgebrachte ständige oder Verkehrslast auf die Stützwand gleichmäßig ist und davon ausgegangen werden kann, dass es sich um eine unendlich verteilte Last handelt, im Ruhezustand = k_. im Ruhezustand = k_, Die Position der Resultierenden liegt in der Mitte der Gesamthöhe der Wand. Bei einer geneigten Verfüllung, Die Druckverteilung weist einen Winkel auf, der der Neigung der Hinterfüllung entspricht. Für diesen Fall, die Berechnung der Resultierenden geht wie folgt:
- Für Boden im Ruhezustand:
\(P_{dist, \; im Ruhezustand} = K_{0} \cdot q cdot H_{Boden}\)
- im Ruhezustand = k_:
\(P_{dist, \; Unterbau Erde} = K_{ein} \cdot q cdot H_{Boden}\)
- im Ruhezustand = k_:
\(P_{dist, \; passiv} = K_{p} \cdot q cdot H_{Boden}\)
Wie bereits erwähnt, da die Verteilung gleichmäßig ist, die Lage der Resultierenden liegt genau in der Mitte der Bodenhöhe.
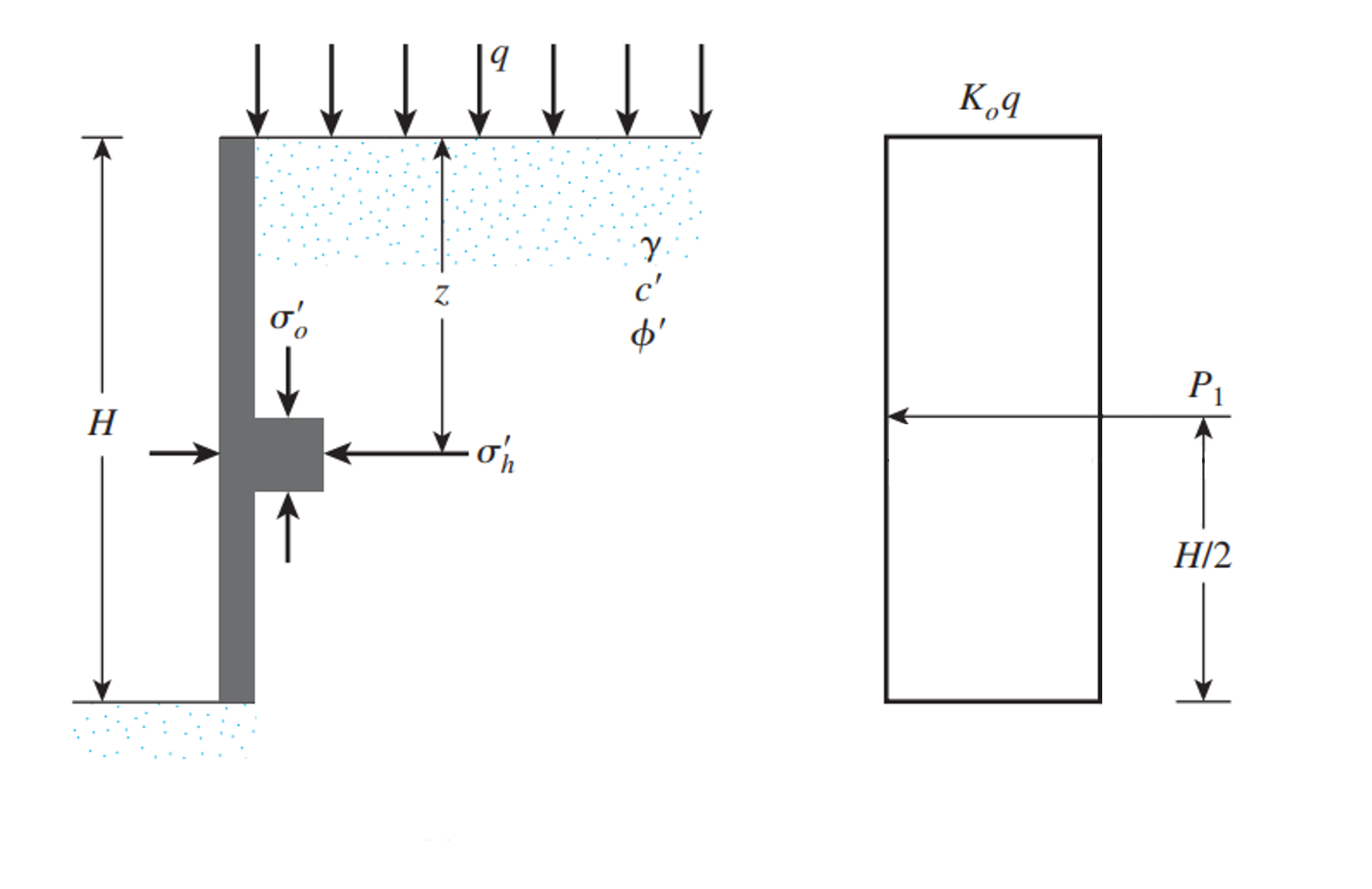
Angepasst von: Das, B.. M.. (2010). Grundlagen des Grundbaus, SI-Ausgabe. Kapitel 7 Seitlicher Erddruck. Cengage-Lernen. Zahl 7.3
Patch laden
Für den Fall einer Fleck- oder Streifenzuschlagslast auf einer Stützmauer, Die Gesamtkraft pro Längeneinheit kann ausgedrückt werden als:
\(P_{Patch} = frac{q}{90} [H.(\theta_2-theta_1)]\)
wo,
\(\theta_1 = hell^{-1}(\frac{b'}{H.}) (Sie)\)
\(\theta_2 = tan^{-1}(\frac{ein’ + b'}{H.}) (Sie)\)
Diese resultierende Kraft aus dem seitlichen Erddruck aufgrund einer Flächen- oder Streifenlast liegt bei \(\Bar{mit}\) gemessen von der Unterseite der Druckverteilung, \(\Bar{mit}\) kann unter Verwendung des folgenden Ausdrucks geschätzt werden:
\(\Bar{mit} = H – [\frac{H^2(\theta_2-theta_1) + (RQ) – 57.3Ah}{2H.(\theta_2-theta_1)}]\)
Wo \(R = (a’+b’)^2cdot(90 – \theta_2)\) sowie \(Q = b’^2(90-\theta_1)\)
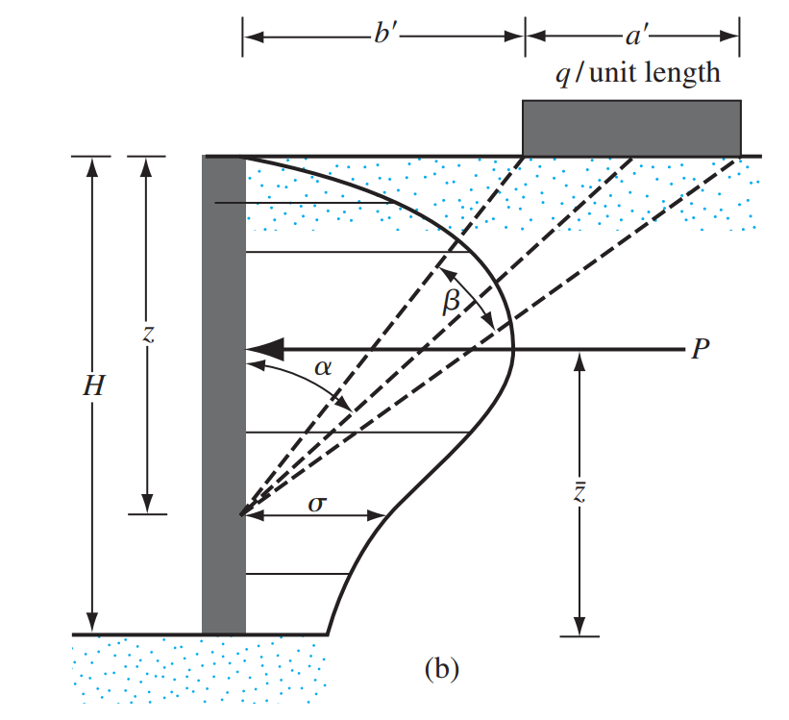
Genommen von: Das, B.. M.. (2010). Grundlagen des Grundbaus, SI-Ausgabe. Kapitel 7 Seitlicher Erddruck. Cengage-Lernen. Zahl 7.14
Linienlast
Schließlich, für den Fall einer Linienauflast auf einer Stützmauer, die Spannung auf der Rückseite einer Stützmauer in jeder Tiefe \([object Window]), kann ausgedrückt werden als:
\(\Sigma = frac{4q}{\ft H} \frac{a^2 b}{(a^2 + b^2)^ 2}\) für \(ein > 0.4\)
\(\Sigma = frac{q}{H.} \frac{0.203 b}{(0.16+ b^2)^ 2}\) für \(ein leq 0.4\)
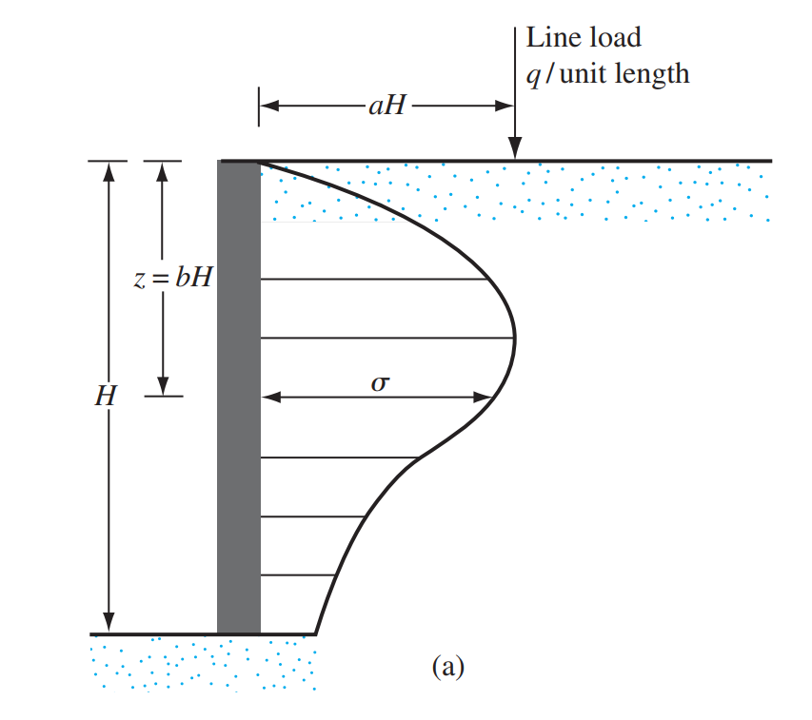
Genommen von: Das, B.. M.. (2010). Grundlagen des Grundbaus, SI-Ausgabe. Kapitel 7 Seitlicher Erddruck. Cengage-Lernen. Zahl 7.14
Integrieren Sie die obigen Ausdrücke aus \(b = 0\) zu \(b = 1\), Es ist möglich, den Wert der resultierenden Kraft aufgrund der Spannungsverteilungen der aufgebrachten Linienlast zu erhalten:
\(P_{Linie} = int_{0}^{H.}\Sigma ,dz = – \frac{4 H^2 ein^{2} q}{2 H^2 ein^{2} \Pi + 2 H^2 pi} + \frac{2 q}{\Pi} = frac{2 q}{\pi links(ein^{2} + 1\richtig)}\) für \(ein > 0.4\)
\(P_{Linie} = int_{0}^{H.}\Sigma ,dz = 0.546875 q \) für \(ein leq 0.4\)
Zur Berechnung des Orts der resultierenden Kraft, die Anfangsausdrücke für die Spannung in jeder Tiefe werden über zwei Intervalle integriert, eins von \(b = 0\) zu \(b = b_r) und die andere von \(b = b_r) zu \(b = 1\), danach, beide Ausdrücke werden in eine Gleichung eingesetzt und ihre Lösung ist der Ort der resultierenden Kraft aus der seitlichen Druckverteilung:
\(\Bar{mit} = H links(1 – ein sqrt{\frac{1}{2 ein^{2} + 1}}\richtig)\) für \(ein > 0.4\)
\(\Bar{mit} = H (1- 0.348155311911396) \) für \(ein leq 0.4\)
Fazit
Die korrekte Abschätzung der resultierenden Kraft des seitlichen Erddrucks aufgrund überlagerter Lasten und ihrer Lage ist ein entscheidender Schritt im Planungsprozess für Stützmauern. Weitere Informationen darüber, wie dieser seitliche Erddruck in den Konstruktionsprozess für Stützmauern einbezogen wird, siehe Artikel Hier.
Abgesehen vom seitlichen Erddruck durch Auflasten, Das Eigengewicht des Bodens übt auch Druck auf die Rückseite der Stützmauer aus, die Einzelheiten zur Berechnung dieses Drucks für verschiedene Bodenbedingungen, z. B. im Ruhezustand, Unterbau Erde, und passiv werden in einem anderen Artikel behandelt Hier.
Verweise
Stützmauer-Rechner
SkyCiv bietet einen kostenlosen Stützmauerrechner an, der den seitlichen Erddruck auf die Wand berechnet, und führen Sie eine Standsicherheitsanalyse Ihrer Stützmauern durch. Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des, Die Hälfte der Wandhöhe von der Unterseite der Basis für den Fall des, wie man die Standsicherheit einer Stützmauer gegen Umkippen berechnet, Gleiten, und Lager!
Produkt Entwickler
BEng (Bürgerlich)