Allgemeine Beschreibung
SkyCiv hat eine neue leistungsstarke Funktion in die Plattform integriert, die aus der Analyse des Plattenreaktionsspektrums besteht. In diesem Artikel, Wir werden ein Beispiel eines kleinen Gebäudes behandeln, wie das folgende Bild zeigt. Der Hauptzweck besteht darin, einige wesentliche Details zu erläutern, wenn Sie eine ähnliche Analyse selbst durchführen.
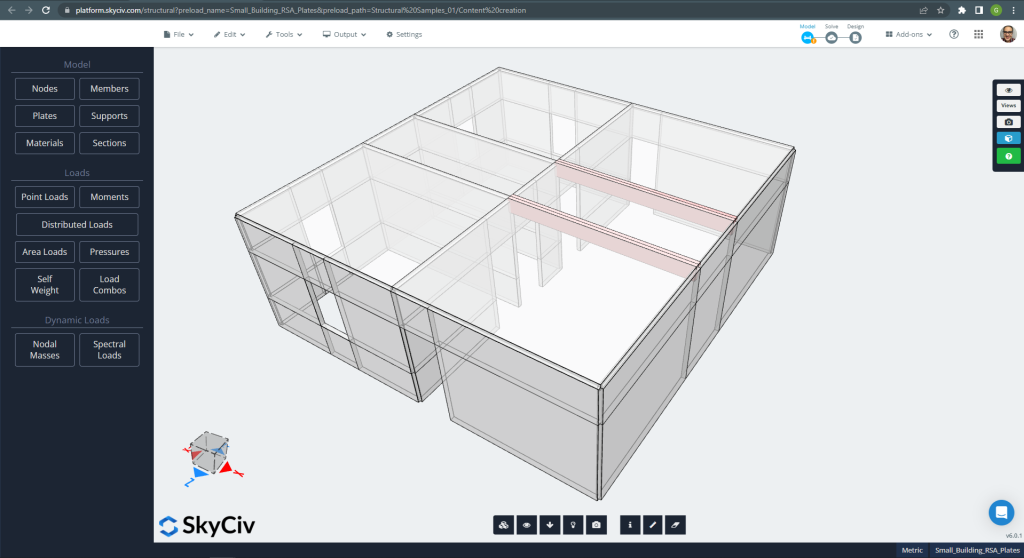
Abbildung 1. Beispiel für ein kleines Gebäude
Sie können sehen, dass die Wände und Decken der kleinen Stahlbetonkonstruktion aus dem SkyCiv-Plattenelement bestehen. Bei der Auslegung des Gebäudes für dynamische Belastungen wie Erdbeben, In den meisten Bauvorschriften sind einige Methoden festgelegt, beispielsweise das „Antwortspektrumverfahren“ oder die „Antwortspektrumsanalyse“. (RSA).’
Die RSA besteht darin, die Beschleunigung auf seismischer Auslegungsebene durch eine durch den Code vorgegebene glatte Kurve zu nehmen. Sie können diese SkyCiv-Artikel lesen: Antwortspektrumanalyse: Ein Gebäudebeispiel und eine Analyse des Antwortspektrums: Weitere Informationen und Beispiele finden Sie unter Modale Kombinationsmethoden Antwortspektrumanalyse: Baubeispiele und Antwortspektrumanalyse: Modale Kombinationsverfahren.
Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!
Finite-Elemente-Modell: Dynamische Plattenanalyse
Sobald die Geometrie und Materialien für das Beispiel definiert sind, Der nächste entscheidende Schritt besteht darin, eine lineare Analyse einer vernetzten Struktur durchzuführen. Bitte schauen Sie sich das Modell in der Abbildung an 2.
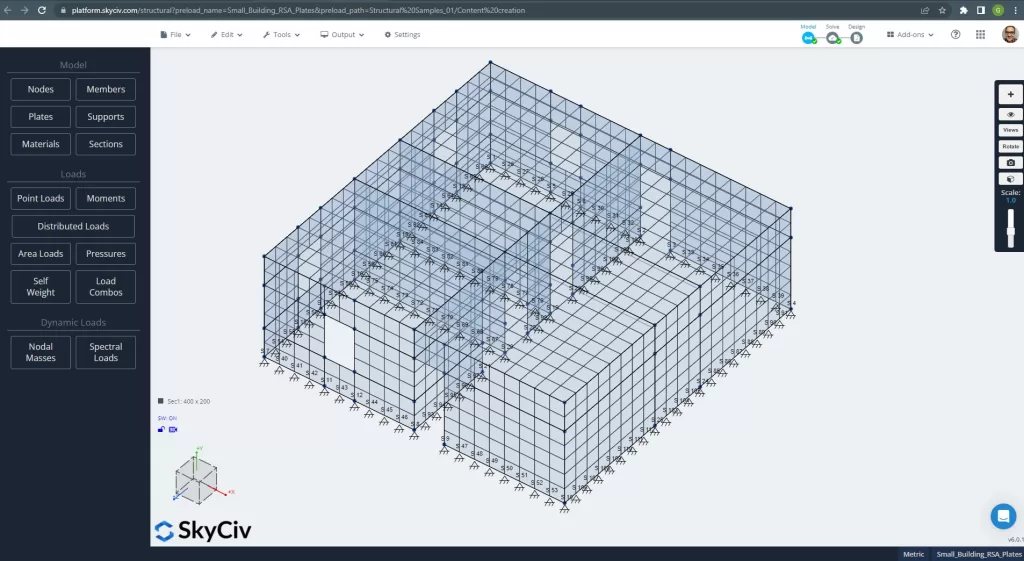
Abbildung 2. Vermaschtes kleines Gebäude
Die Bewegungsgleichung, die bei der Durchführung einer Antwortspektrumanalyse gelöst werden muss, hat die Form:
\({Mich}{\Punkt{X_e}}+{C_e}{\Punkt{X_e}}+{K_e}{X_e}={-\Punkt{X_0}{(t)}{Mich}{J.}}\)
Wo:
- \({Mich}\) ist die konsistente Matrix für Massen.
- \({C_e}\) ist die Dämpfungsmatrix (Häufig, Dieser Wert könnte als lineare Kombination von Steifigkeits- und Massenmatrizen berechnet werden \({C_e}={\Alpha}{K_e}+{\Beta}{M.}\) ).
- \({K_e}\) ist die Steifigkeitsmatrix.
- \({X_e}\) ist der Verschiebungsvektor relativ zur Basis der Struktur.
- \({X_0}{(t)}\) ist der Bodenverschiebungsvektor (Es verfügt über alle Freiheitsgrade: 3 Verschiebungen und drei Rotationen).
- \({J.}\) ist ein Vektor mit einheitlichen Komponenten.
Due SkyCiv verwendet die Finite-Elemente-Methode für Platten, die Matrix \({Mich}\) könnte durch den folgenden Ausdruck für kinetische Energie erhalten werden:
\({E_c}={\frac{1}{2}}{\int_{Bd} {\rho}{\Punkt{x}^ 2}{dw}Vol}\) .
Wir schreiben jetzt das \(x ) Berechnen Sie die Verschiebung als Funktion ihrer Knoten und verwenden Sie einige Interpolationsausdrücke (\(N_{x}^{T.}\)).
\({x}=N_{x}^{T.} {x}\). Wenn wir diesen Wert in die Energiegleichung einsetzen, ,:
\({E_c}={\frac{1}{2}}{\Punkt{x}^{T.}}\{{\int_{Bd}{\rho}{N.}{N^T}{d}{Vol}}\} \Punkt{x} \)
So, Wir können das sagen:
\( M = {\int_{Bd}{\rho}{N.}{N^T}{d}{Vol}}\)
Durch die Definition der obigen Matrix können wir eine Modalanalyse durchführen, welches für die dynamische Analyse benötigt wird. Abbildung 3 hilft uns mit einigen empfohlenen Eingaben.
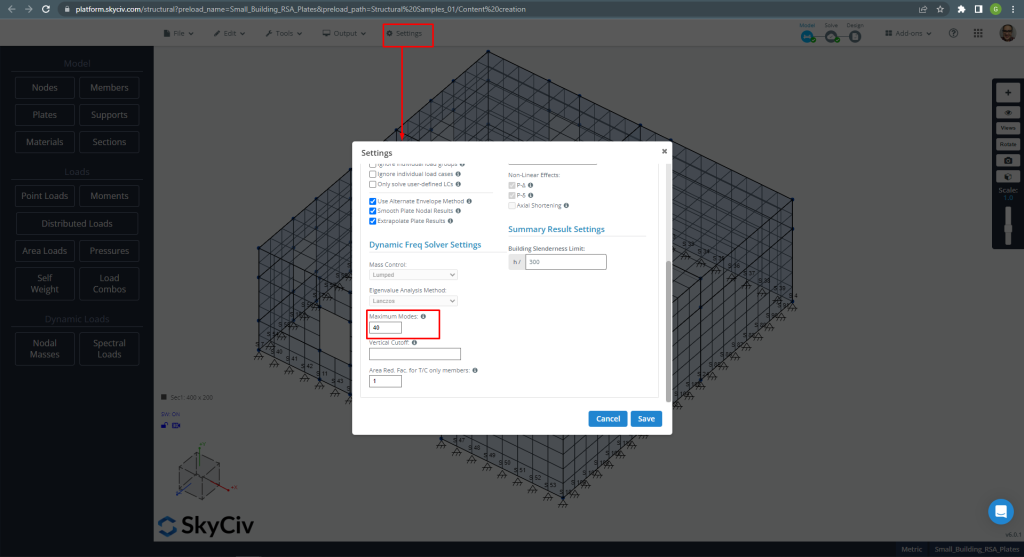
Abbildung 3. Maximal berücksichtigte Modi erhöht bis zu 40
Es wird empfohlen, die Gesamtzahl der Modi zu erhöhen, bis die Codes strikt erfüllt sind. Dies wirkt sich auf die Gesamtmassenbeteiligungsfaktoren aus, die einen Wert von erreichen müssen 90%.
Anwenden seismischer Lasten
Im nächsten Schritt werden die Spektrallasten definiert. Wir können eine benutzerdefinierte Funktion einbinden oder die zuvor von der SkyCiv-Plattform erstellten Fälle übernehmen. In diesem Beispiel wird für jede Bauplan-Hauptrichtung ein ASCE-Grundstück verwendet. Überprüfen Sie die Eingaben in Abbildung 4 und Abbildung 5.
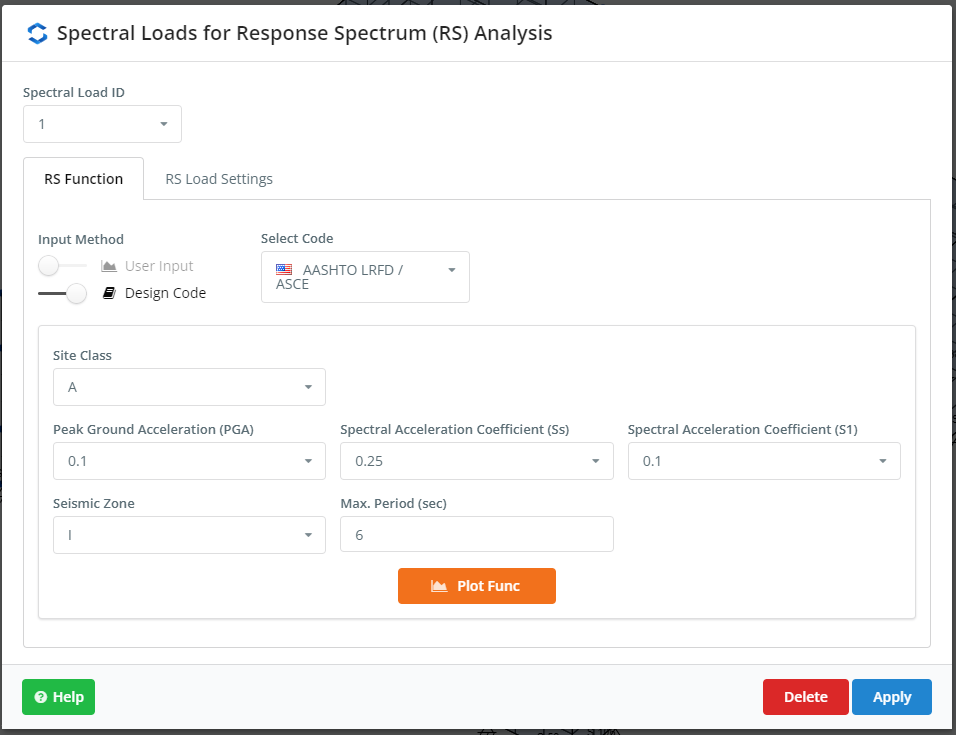
Abbildung 4. Einstellungen für RSA, Teil eins
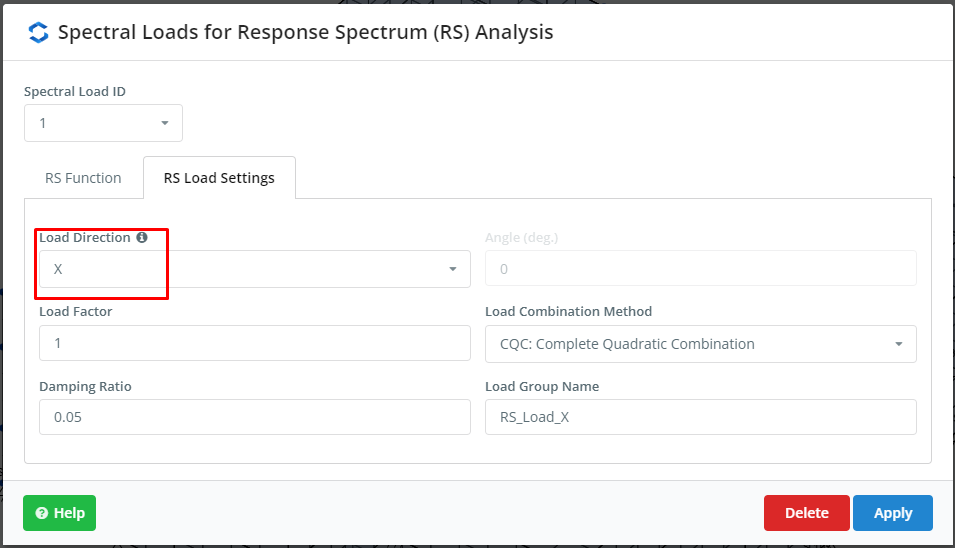
Abbildung 5. Einstellungen für RSA, Zweiter Teil
Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!
Ergebnisanalyse und Schlussfolgerungen
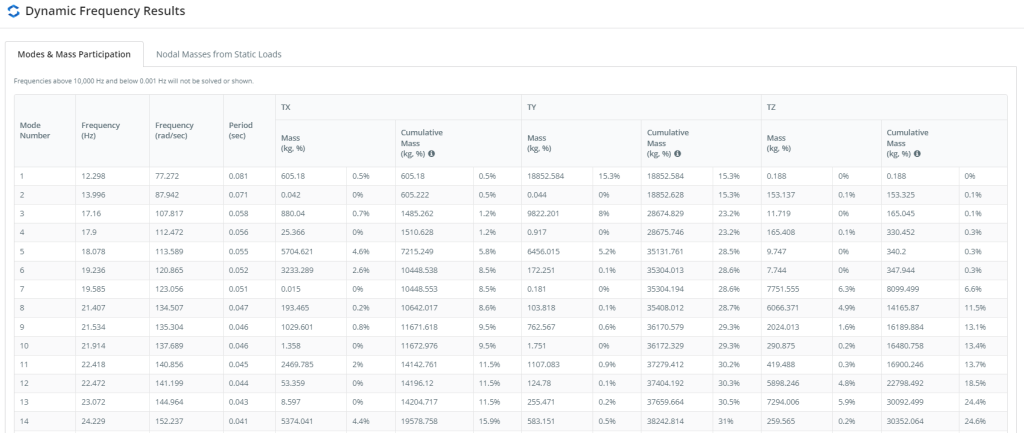
Abbildung 6. Zusammenfassung der Modi und der Massenbeteiligung, Teil eins
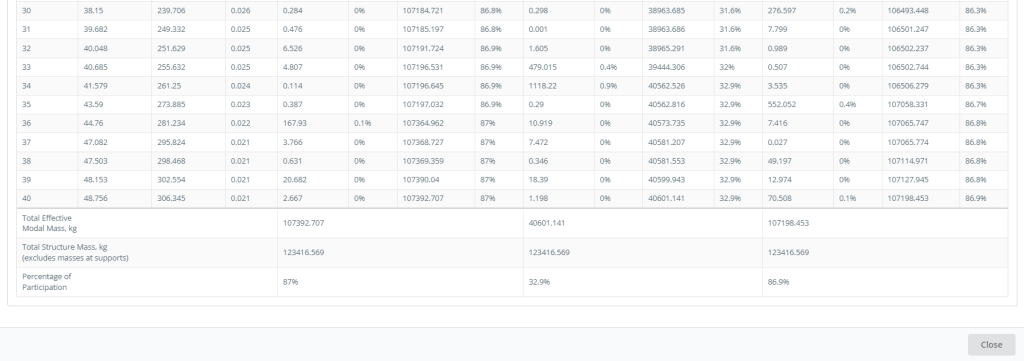
Abbildung 7. Zusammenfassung der Modi und der Massenbeteiligung, Teil eins
Zahlen 6 und 7 Geben Sie die Modi und Massenbeteiligungswerte an. Diese Tabellen definieren die Hauptmoden in jeder Planrichtung, die denen mit den höchsten Massenbeteiligungswerten entsprechen.
Modus 24, T = 0.029 Sekunden, Massenbeteiligung = 44.80 % „x-Richtung“:
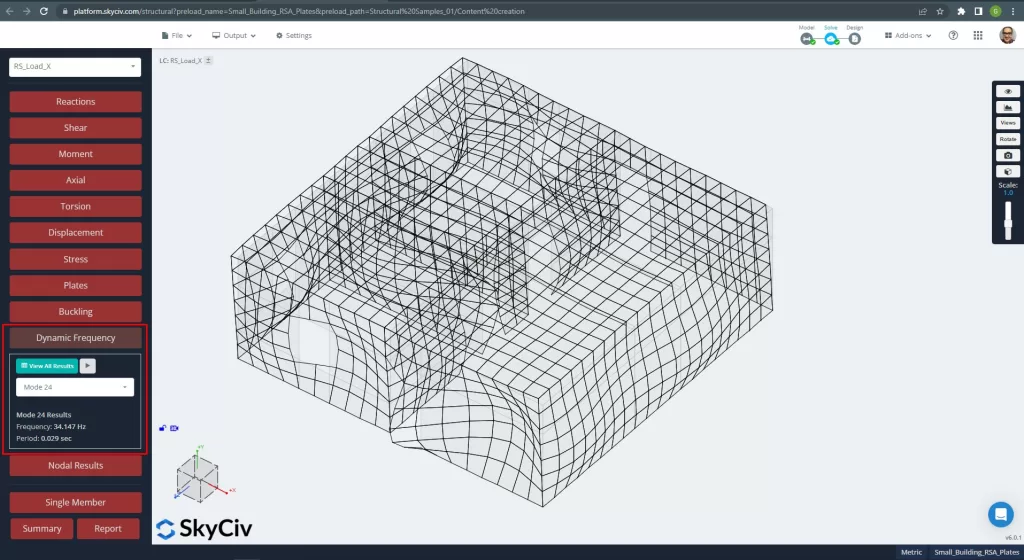
Abbildung 8. Hauptmodalmodus für die X-Richtung.
Modus 23, T = 0.030 Sekunden, Massenbeteiligung = 41.80 % „Z-Richtung“:
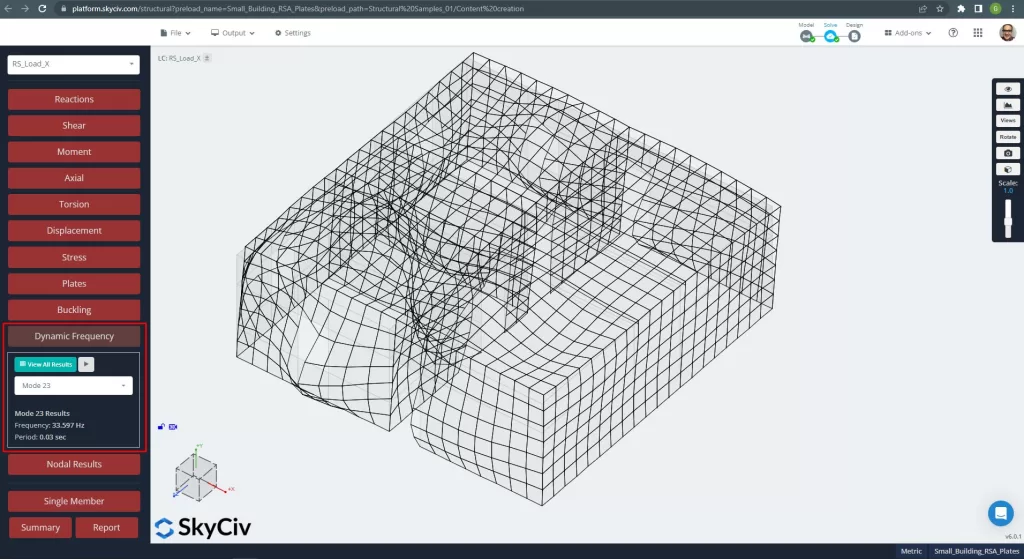
Abbildung 9. Hauptmodalmodus für Z-Richtung.
SkyCiv gibt auch die Verschiebungen an, Kräfte, betont, und so weiter, wenn der RSA ausgeführt wird. Die folgenden Bilder helfen uns zu verstehen, wie sich die Gebäude verhalten.
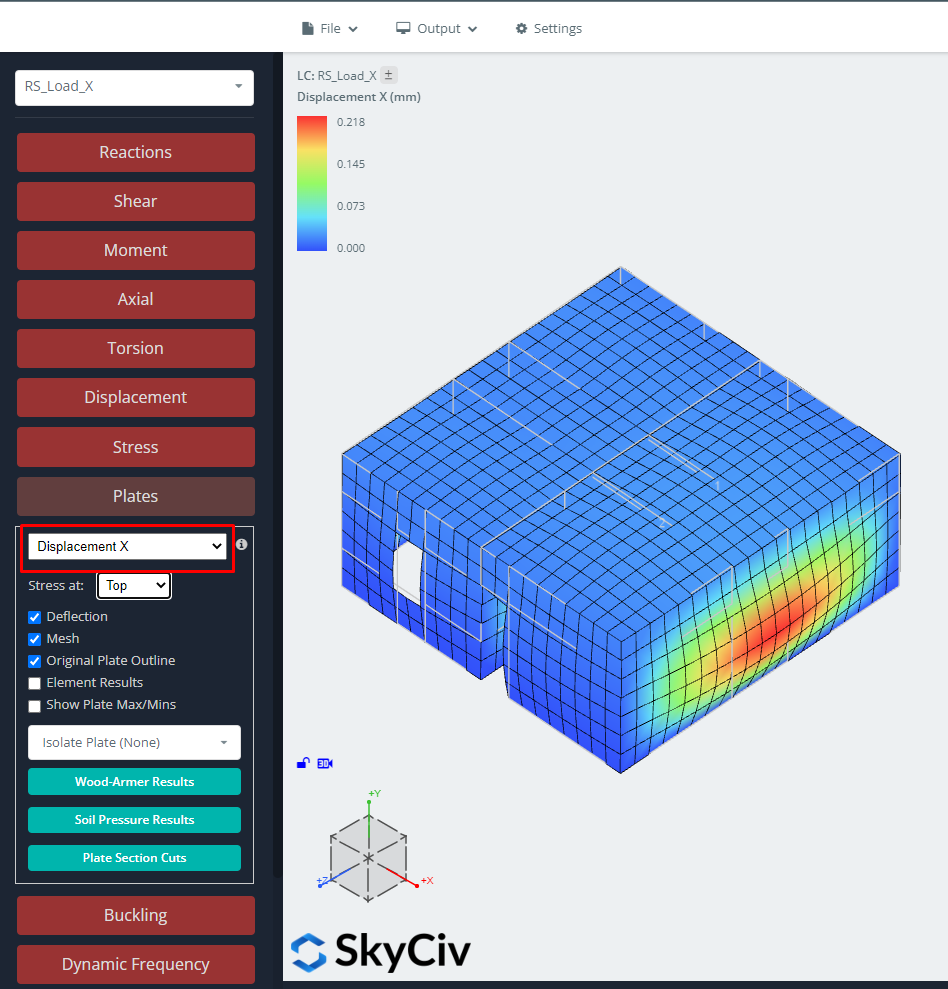
Abbildung 10. Verschiebungen in X-Richtung für RSA-Lastfall.
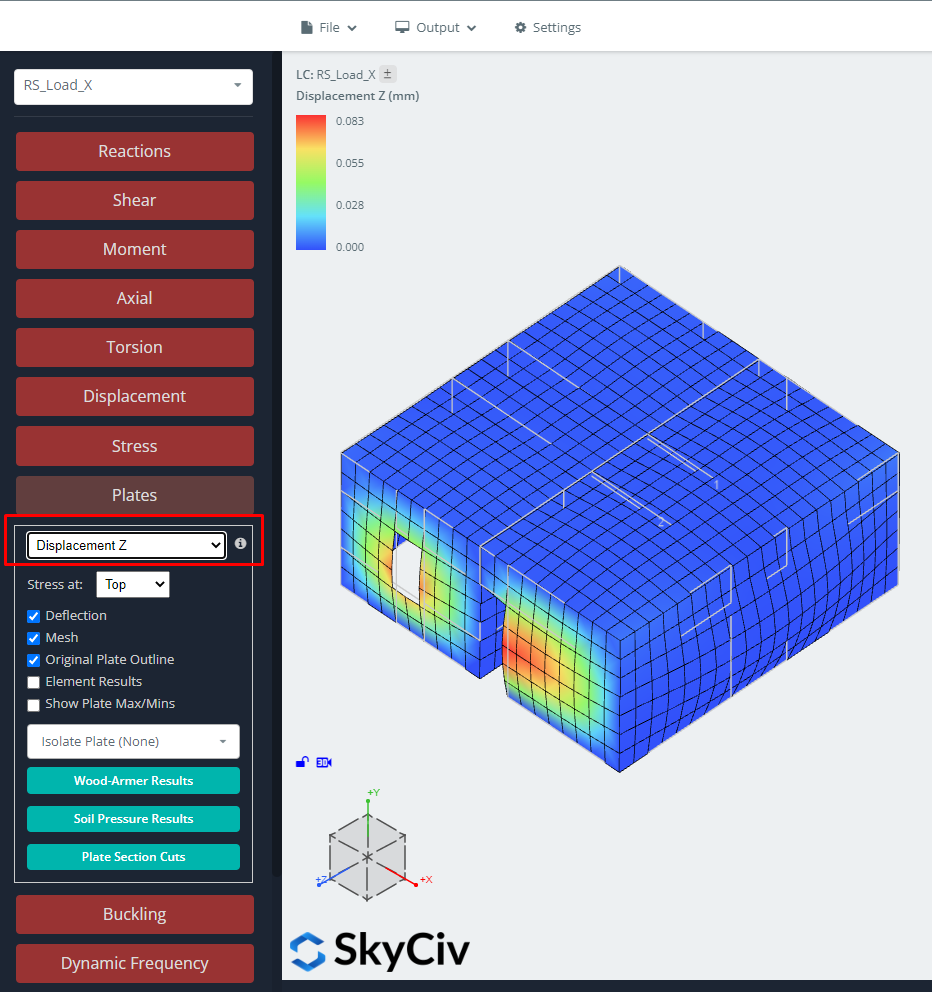
Abbildung 11. Verschiebung in Z-Richtung für RSA-Lastfall.
Mit diesen Ergebnissen können Sie nun die Plattenelemente entwerfen. Wir empfehlen Ihnen, die SkyCiv-Artikel über Plattendesign zu lesen: Plattendesign-Modul und Beispiele für angewandte Code-basierte Platten finden Sie in den folgenden Links: ACI, AS-3600 und Eurocode 2.
Ebenfalls, mit SkyCiv, Wir können die Basisreaktionen für den Fundamententwurf ermitteln.
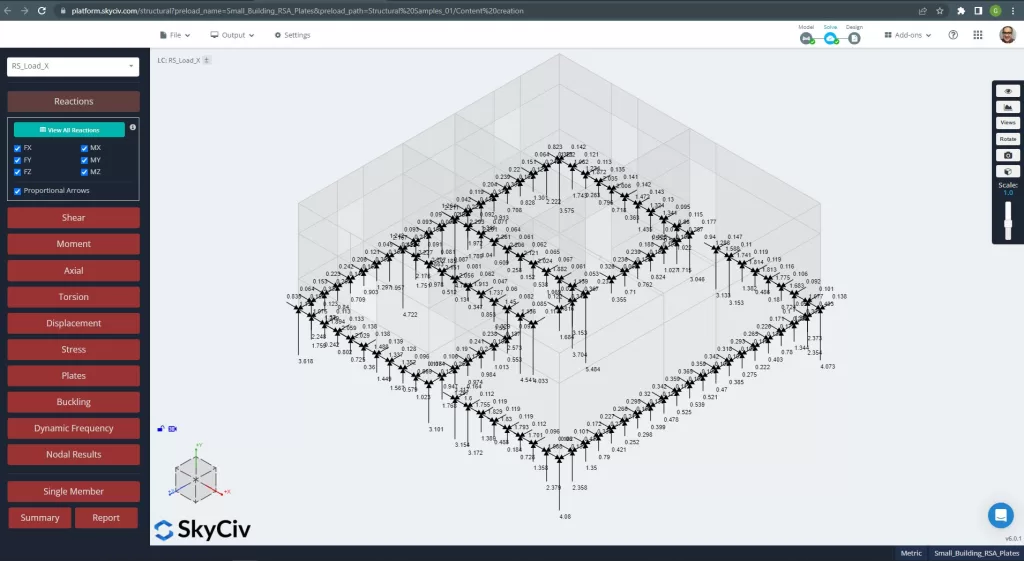
Abbildung 12. Basisreaktionen für RSA-Lastfall.
Achten Sie einfach auf die Ergebniszeichen! Alle wurden in positiven oder absoluten Werten angegeben. Dies liegt daran, dass wir bei Verwendung einer RSA-Methode die maximalen Absolutwerte für jede Designkomponente erhalten.
Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!


