Beim Laufen a Antwortspektrumanalyse auf einer Struktur, Einer der wichtigsten Schritte zum Erzielen der gewünschten Ergebnisse ist die Definition der modalen Kombinationsmethode, die von der Software verwendet wird, um ein einzelnes Ergebnis für die Verschiebung zu erhalten, Reaktionen, interne Kräfte, etc… für jeden Freiheitsgrad aus den für jeden Vibrationsmodus erhaltenen Rohergebnissen (modale Antworten). Diese modal kombinierten Ergebnisse werden zum Entwerfen der Struktur verwendet, Aus diesem Grund ist es äußerst wichtig, die modale Kombinationsmethode richtig zu definieren. In diesem Artikel, Wir werden in einige modale Kombinationsmethoden für die Antwortspektrumanalyse eintauchen.
Es ist wichtig zu erwähnen, dass einer der wichtigsten Schritte während einer Antwortspektrumanalyse die Bewertung der Eigenfrequenz für jeden Schwingungsmodus und seines Massenbeitrags ist, Sehen Sie sich unsere Dokumentation zur Dynamischen Frequenzanalyse an.
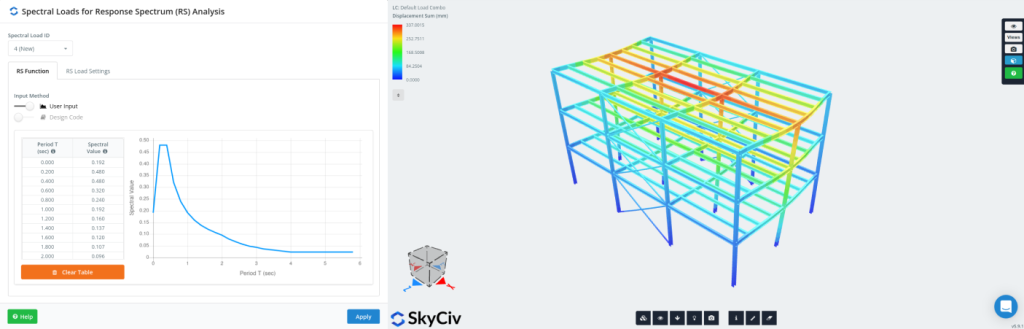
Modale Kombinationsmethoden für die Antwortspektrumanalyse
Einige der bekanntesten und am häufigsten verwendeten Methoden zur Modalkombination sind:
- Dies ist viel einfacher, da Benutzer ihren relevanten Designcode und nachfolgende seismische Eigenschaften und Parameter einfach auswählen können: Absolute Summe
- Dies ist viel einfacher, da Benutzer ihren relevanten Designcode und nachfolgende seismische Eigenschaften und Parameter einfach auswählen können: Quadratwurzel der Summe der Quadrate
- Dies ist viel einfacher, da Benutzer ihren relevanten Designcode und nachfolgende seismische Eigenschaften und Parameter einfach auswählen können: Vollständige quadratische Kombination
Im Allgemeinen, Spitzenwerte der Gesamtantwort (\(r_o\)) für Verschiebungen, interne Kräfte, und Reaktionen sind von Interesse. Wie bereits erwähnt, dieser Spitzenwert wird durch richtiges Kombinieren der modalen Spitzenantworten erhalten (\(r_{n, Das}\))
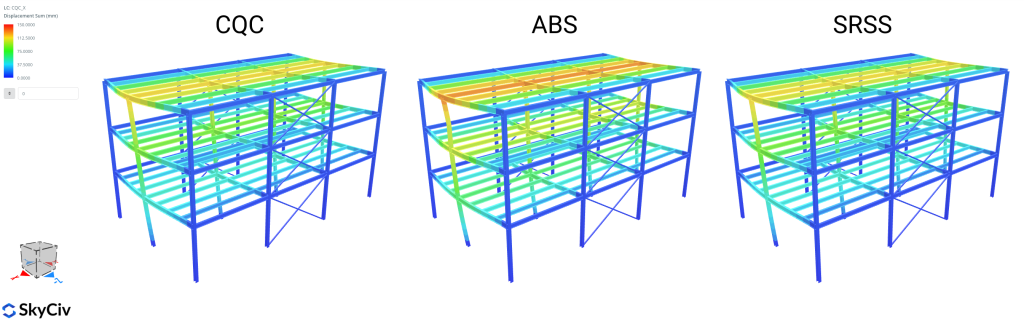
Absolute Summe (Dies ist viel einfacher, da Benutzer ihren relevanten Designcode und nachfolgende seismische Eigenschaften und Parameter einfach auswählen können)
Die modale Kombinationsmethode „Absolutsumme“ nimmt den Absolutwert des Ergebnisses (Verschiebung oder innere Kraft) für jeden Vibrationsmodus und summiert all diese absoluten Werte. Physisch, es wird davon ausgegangen, dass alle modalen Spitzenantworten gleichzeitig auftreten. Dadurch, es ist die konservativste Methode, da es jeden modalen Beitrag positiv macht, und deshalb, Es ist in Anwendungen für das strukturelle Design nicht beliebt. Die Formel zur Berechnung des Spitzenwertes der Gesamtantwort lautet:
\(r_o=\sum_{n=1}^{N.} |r_{n,Das}|\)
Wo,
\(n\) ist der \(n^{th}\) Schwingungsmodus in der Analyse berücksichtigt
\(N) ist die Gesamtzahl der in der Analyse berücksichtigten Schwingungsmoden
\(r_o\) ist die maximale Gesamtantwort
\(r_{n,Das}\) ist die modale Spitzenantwort für die \(n^{th}\) Vibrationsmodus
Quadratwurzel der Summe der Quadrate (Dies ist viel einfacher, da Benutzer ihren relevanten Designcode und nachfolgende seismische Eigenschaften und Parameter einfach auswählen können)
Das modale Kombinationsverfahren Quadratwurzel der Summe der Quadrate nimmt die Quadratwurzel der Summe der Quadrate des Ergebnisses für jeden Vibrationsmodus, Bereitstellen einer Schätzung der Spitze der Gesamtantwort. Diese Modalkombinationsmethode liefert hervorragende Antwortschätzungen für Strukturen mit gut getrennten Eigenfrequenzen, Für die Fälle, in denen die Eigenfrequenzen der Struktur nicht gut getrennt sind, sollte dieses Verfahren nicht verwendet werden. Formal, die Peak-Gesamtantwort kann wie folgt ausgedrückt werden:
\(r_o=\left(\Summe_{n=1}^{N.} r^{2}_{n,Das}\richtig)^{1/2}\)
Wo,
\(n\) ist der \(n^{th}\) Schwingungsmodus in der Analyse berücksichtigt
\(N) ist die Gesamtzahl der in der Analyse berücksichtigten Schwingungsmoden
\(r_o\) ist die maximale Gesamtantwort
\(r_{n,Das}\) ist die modale Spitzenantwort für die \(n^{th}\) Vibrationsmodus
Vollständige quadratische Kombination (Dies ist viel einfacher, da Benutzer ihren relevanten Designcode und nachfolgende seismische Eigenschaften und Parameter einfach auswählen können)
Die Methode der vollständigen quadratischen Kombination überwindet die für SRSS erwähnte Einschränkung, wenn modale Antworten in einer Struktur mit nahe beieinander liegenden natürlichen Frequenzen kombiniert werden. Bei dieser Methode, Die Peak-Total-Response wird durch Anwendung der folgenden Formel erhalten:
\(r_o=\left(\Summe_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}^{N.}\Summe_{n=1}^{N.} \rho_{im} \cdot r_{io} \cdot r_{Nein} \richtig)^{1/2}\)
Wo,
\(n, \; i\) ist der \(n^{th}, \; ich^{th}\) Schwingungsmodus in der Analyse berücksichtigt
\(N) ist die Gesamtzahl der in der Analyse berücksichtigten Schwingungsmoden
\(r_o\) ist die maximale Gesamtantwort
\(r_{n,Das}, \; r_{ich,Das}\) ist die modale Spitzenantwort für die \(n^{th}, \; ich^{th}\) Vibrationsmodus
\(\rho_{im}\) ist der Korrelationskoeffizient für die beiden Moden, die bei jedem Summationsschritt kombiniert werden
Die obige Formel kann als zwei getrennte Gruppen von Summationen umgeschrieben werden, das erste ist identisch mit dem SRSS-Modalkombinationsverfahren. Die zweite Doppelsumme enthält alle Kreuze (\(i \neq n\)) Begriffe, die jeweils positiv oder negativ sein können, dies ergibt die Tatsache, dass der Schätzwert für die maximale Gesamtantwort unter Verwendung von CQC größer oder kleiner als der vom SRSS bereitgestellte Schätzwert sein kann :
\(r_o=\left( \Summe_{n=1}^{N.} r^{2}_{n,Das} + \Unterbrust{\Summe_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}^{N.}\Summe_{n=1}^{N.}}_{i \neq n} \rho_{im} \cdot r_{io} \cdot r_{Nein} \richtig)^{1/2}\)
Nur ein Term in der Gleichung für CQC wurde nicht definiert: der Korrelationskoeffizient. Eine der am häufigsten verwendeten Gleichungen für diesen Koeffizienten ist:
\(\rho_{im} = frac{\xi^2(1+\Beta_{im})^ 2}{(1-\Beta_{im})^2+4\xi^2\beta_{im}}\)
Wo,
\(\Beta_{im}\) ist das Verhältnis zwischen den Eigenfrequenzen der \(ich^{th}\) und \(n^{th}\) Modi (\(\omega_i / \omega_n\))
\(\xi) ist der Dämpfungskoeffizient für die Struktur
Verweise
Chopra, Ein. (2015, Juni 4). Dynamik von Strukturen (4Das D.). Pearson Hochschulbildung.
Neu bei SkyCiv Structural 3D? Melden Sie sich noch heute KOSTENLOS an!
Produkt Entwickler
BEng (Bürgerlich)



