Calcolo della pressione laterale del terreno su un muro di contenimento
Uno dei principali carichi che agiscono su un muro di contenimento è la pressione laterale del terreno. Per tale motivo, fare una buona stima della sua grandezza e distribuzione è decisivo nella progettazione di un muro di contenimento in calcestruzzo. In generale, esistono tre diversi tipi di pressione laterale del terreno a seconda della direzione in cui il muro tende a muoversi:
- Pressione del terreno a riposo: Quando il muro è completamente trattenuto dal muoversi
- Pressione attiva del terreno: Quando il muro può inclinarsi lontano dal terreno trattenuto
- Pressione di terra passiva: Quando il muro può essere spinto nel terreno trattenuto
In questo articolo, ci concentreremo sulla descrizione delle formule per ciascuno dei casi di pressione terrestre sopra menzionati.
Distribuzione della pressione laterale del terreno
In generale, la pressione laterale del terreno si comporta come la pressione idrostatica. Avere un valore nullo in superficie e un valore massimo nel punto più profondo seguendo una distribuzione lineare tra i due bordi menzionati. Pertanto, la distribuzione orizzontale delle sollecitazioni subsuperficiali è descritta dalla seguente espressione:
\(\sigma_h = K_* \cdot (\gamma z)\)
Dove \(K_*\) assume il valore di \(K_o\) per il caso di pressione a riposo, \(K_a\) per il caso di pressione attiva, e \(K_p\) per il caso di pressione passiva.
Integrando l'espressione data per la sollecitazione laterale del sottosuolo da \(0\) per \(H\) pollici \(z), il risultante risulta essere:
\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)
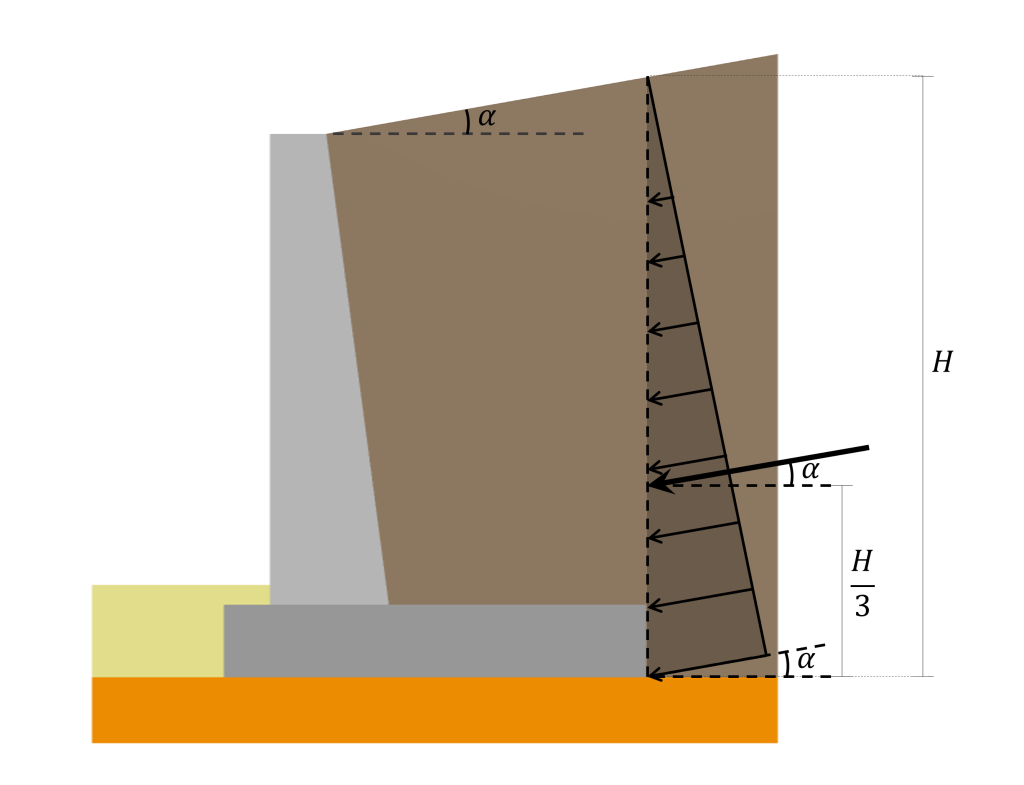
Si trova la linea di azione di questa risultante \(\frac{2}{3}H\) dalla superficie. La distribuzione della pressione laterale del terreno, la sua risultante, e la posizione sopra descritte sono illustrate nella figura seguente:
È importante ricordare che la distribuzione presentata e l'approccio di calcolo risultante si applicano solo alle pressioni del suolo che agiscono su una superficie verticale. Nel caso di un muro di contenimento con faccia posteriore inclinata (come quello nella foto sopra), la superficie su cui agisce la pressione del suolo è ancora considerata verticale in quanto si assume che agisca su un piano verticale situato dove termina il tallone.
Inoltre, quando il rinterro è inclinato di una certa angolazione \(\alpha\) rispetto all'orizzontale, la distribuzione della pressione e la sua risultante sono inclinate dello stesso angolo \(\alpha\) come illustrato di seguito:
La corretta stima della distribuzione della pressione laterale del terreno e la sua risultante è una fase cruciale nel processo di progettazione del muro di sostegno. Per ulteriori informazioni su come questa pressione laterale del terreno è inclusa nel processo di progettazione del muro di contenimento, fare riferimento all'articolo Qui. Passiamo ora alle formule per il calcolo della risultante pressione laterale del terreno esercitata su un muro di contenimento dal terreno nelle diverse condizioni.
Pressione terrestre laterale a riposo
Questo approccio per il calcolo della pressione laterale del terreno contro un muro di contenimento può essere utilizzato solo se il muro è completamente fermo e non è consentito allontanarsi dal suolo o nel terreno, questa condizione assicura che la deformazione orizzontale nel terreno sia nulla. Per questo caso, il coefficiente di pressione a riposo (\(K_o\)) è quello che sostituisce \(K_*\) nelle equazioni precedenti. Tale coefficiente è l'unica incognita per il calcolo della distribuzione della pressione e della sua risultante. Per terreno normalmente consolidato, la relazione per \(K_o\) è:
\(K_o = 1-peccato(\phi')\)
Dove \(\phi') è l'effettivo angolo di attrito del terreno considerato.
Per terreno sovraconsolidato, il coefficiente può essere calcolato utilizzando la seguente espressione:
\(K_o = (1-senza(\phi'))\cpunto OCR^{senza(\phi')}\)
Dove \(\phi') è l'angolo effettivo di attrito, e \(OCR\) il rapporto di sovraconsolidamento del terreno considerato.
Inserendo questo coefficiente nell'espressione per calcolare la forza risultante dalla pressione terrestre laterale a riposo si ottiene a:
\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)
Pressione attiva laterale del terreno
L'approccio precedente può essere utilizzato quando il muro non cede affatto, però, se un muro tende ad allontanarsi dal suolo, la pressione del suolo sul muro a qualsiasi profondità diminuirà. Per questo caso, il coefficiente di pressione attiva (\(K_a\)) è quello che sostituisce \(K_*\) nelle equazioni iniziali. Usando l'approccio di Rankine per a riempimento granulare, e supponendo che la pressione agisca in a dorso verticale, il coefficiente di pressione del suolo attivo può essere calcolato utilizzando l'equazione:
\(K_a=cos(\alfa) \frac{cos(\alfa) – \sqrt{cos^2(\alfa) – cos^2(\phi')}}{cos(\alfa) + \sqrt{cos^2(\alfa) – cos^2(\phi')}}\)
Dove \(\phi') è l'angolo di attrito del terreno in considerazione e \(\alpha\) è l'angolo di inclinazione della superficie del rinterro rispetto all'orizzontale.
Inserendo questo coefficiente nell'espressione per il calcolo della forza risultante dalla pressione laterale del terreno in condizioni attive si ottiene a:
\(P_a=\frac{1}{2} \gamma \cdot H^2 \cdot K_a\)
I calcoli della pressione attiva Rankine presentati in precedenza si basano sul presupposto che il muro sia privo di attrito.
Pressione laterale passiva del terreno
La pressione laterale del terreno che agisce su un muro di contenimento è considerata passiva quando il muro viene spinto nella massa del terreno, in quella condizione, la sollecitazione orizzontale aumenterà rispetto alla condizione di riposo. Per questo caso, il coefficiente di pressione passiva (\(K_p\)) è quello che sostituisce \(K_*\) nelle equazioni iniziali. Usando l'approccio di Rankine per a riempimento granulare, e supponendo che la pressione agisca in a dorso verticale, il coefficiente passivo di pressione del suolo può essere calcolato utilizzando le espressioni:
Quando il rinterro è completamente orizzontale
\(K_p = tan^2(45º+\frac{\phi'}{2})\)
Quando il rinterro è inclinato di un certo angolo rispetto all'orizzontale
\(K_p=cos(\alfa) \frac{cos(\alfa) + \sqrt{cos^2(\alfa) – cos^2(\phi')}}{cos(\alfa) – \sqrt{cos^2(\alfa) – cos^2(\phi')}}\)
Dove \(\phi') è l'angolo di attrito del terreno in considerazione e \(\alpha\) è l'angolo di inclinazione della superficie del rinterro rispetto all'orizzontale.
Inserendo questo coefficiente nell'espressione per calcolare la forza risultante dalla pressione laterale del terreno in condizioni passive si ottiene a:
\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)
Ancora una volta, i calcoli della pressione attiva Rankine presentati in precedenza si basano sul presupposto che il muro sia privo di attrito.
Riferimenti
Calcolatrice per muro di sostegno
SkyCiv offre un calcolatore del muro di sostegno gratuito che calcolerà la pressione laterale del terreno sul muro, ed eseguire un'analisi di stabilità sui muri di sostegno. Metà dell'altezza del muro dal fondo della base per il caso del, Metà dell'altezza del muro dal fondo della base per il caso del, come calcolare la stabilità di un muro di sostegno al ribaltamento, scorrevole, e cuscinetto!
Sviluppatore del prodotto
BEng (Civile)