Inhaltsverzeichnis

• Berechnung des Biegemomentdiagramms
• Berechnung des Biegemomentdiagramms von Hand
• Zeichenkonvention für Biegemomentdiagramme
• So berechnen Sie die Biegung mit SkyCiv Beam

Berechnung des Biegemomentdiagramms

Im Folgenden finden Sie eine einfache Anleitung zur Berechnung des Biegemomentdiagramms eines einfach gestützten Trägers. Lernen Sie diese Methode, da sie sehr vielseitig ist (und an viele verschiedene Arten von Problemen angepasst werden kann. Die Fähigkeit, das Moment eines Trägers zu berechnen, ist für Bauingenieure eine sehr gängige Praxis und wird häufig in Prüfungen an Hochschulen und Universitäten abgefragt. Es ist gut, gleich zu Beginn festzustellenemerken, dass die SkyCiv Beam Software diese Handberechnungen sofort und automatisch anzeigen kann! Im Anschluss an das heutige Tutorial zeigen wir Ihnen ein Beispiel, das direkt aus dem Handberechnungsmodul in SkyCiv Beam stammt.

Erstens, Was ist ein Biegemomentt? Ein Moment ist eine Rotationskraft, die auftritt, wenn eine Kraft senkrecht auf einen Punkt in einer bestimmten Entfernung von diesem Punkt wirkt. Es wird berechnet als die senkrechte Kraft multipliziert mit dem Abstand vom Punkt. Ein Biegemoment ist einfach die Biegung, die in einem Träger aufgrund eines Moments auftritt.

Bei der Berechnung von Biegemomenten ist es wichtig, zwei Dinge zu beachten; (1) die Standardeinheiten sind Nm und (2) wenn die oberste Faser zusammengedrückt wird, wird die Biegung als positiv betrachtet. Nachdem wir die Definitionen geklärt haben, wollen wir uns nun die Schritte zur Berechnung eines Biegemomentdiagramms ansehen!

Kostenloser Trägerrechner

Berechnung des Biegemomentdiagramms von Hand

1. Berechnen Sie die Reaktionen an den Stützen und zeichnen Sie das Diagramm des freien Körpers (FBD)

Wenn Sie nicht sicher sind, wie Sie Bestimmen Sie die Reaktionen an den Trägern können – sehen Sie sich bitte zuerst diese Anleitung an. Sobald Sie die Reaktionen kennen, zeichnen Sie das Diagramm des freien Körpers und das Scherkraftdiagramm unterhalb des Trägers. Die Berechnung der Momente können Sie schließlich in den folgenden Schritten durchführen:

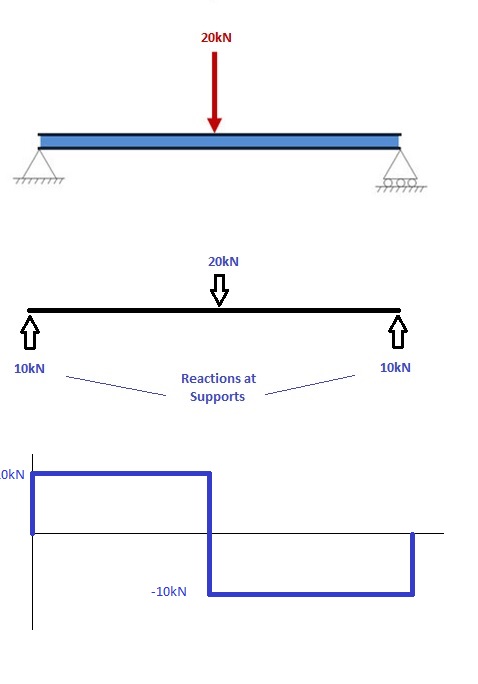
2. Machen Sie von links nach rechts, machen “ "Schnitte" ” vor und nach jeder Reaktion/Ladung

Um das Biegemoment eines Trägers zu berechnen, müssen wir genauso vorgehen wie beim Scherkraftdiagramm. Wir beginnen bei x= 0 bewegen uns über den Träger und berechnen das Biegemoment an jedem Punkt.

Schnitt 1

Machen Sie einen “Schnitt” direkt nach der ersten Reaktion des Trägers. In unserem einfachen Beispiel:

So, wenn wir also den Träger schneiden, berücksichtigen wir nur die Kräfte, die links von unserem Schnitt wirken. In diesem Fall, wir eine Kraft von 10kN in der Aufwärtsrichtung. Wie Sie sich erinnern, ist ein Biegemoment einfach die Kraft x Abstand. Je weiter wir uns also von der Kraft entfernen, desto größer wird das Biegemome. Wir können dies in unserem BMD sehen. Die Gleichung für diesen Teil unseres Biegemomentdiagramms lautet:

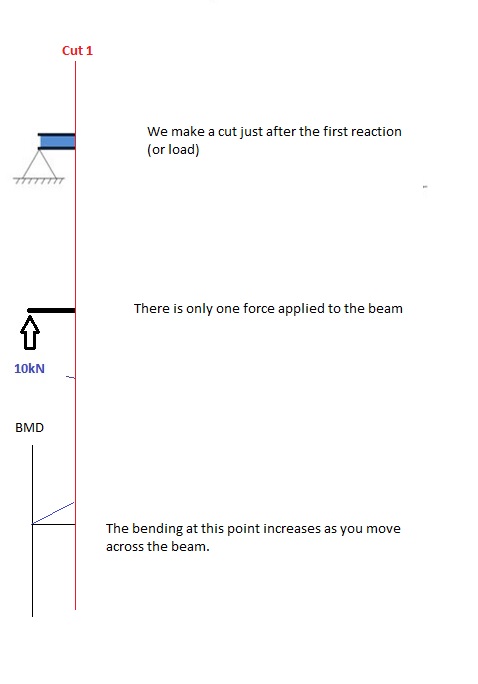
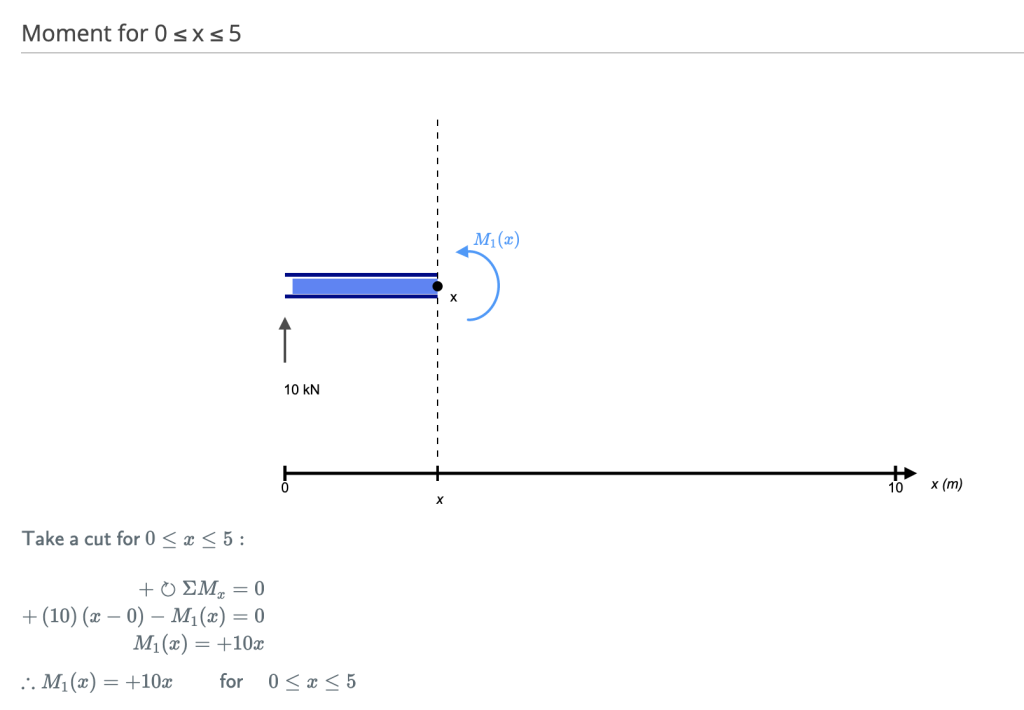
[Quelle: SkyCiv Modul für manuelle Trägerberechnungen]

Schnitt 2

Dieser Schnitt wird kurz vor der zweiten Kraft entlang des Trägers durchgeführt. Da zwischen dem ersten und dem zweiten Schnitt keine weiteren Kräfte wirken, bleibt die Gleichung für das Biegemoment gleich. Das bedeutet, dass wir das maximale Biegemoment (in diesem Fall in der Mitte, oder x = 5) berechnen können, indem wir einfach x=5 in die obige Gleichung einsetzen:

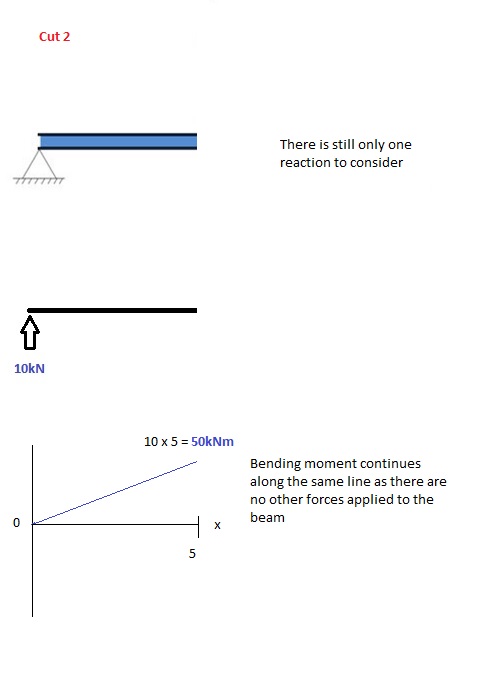
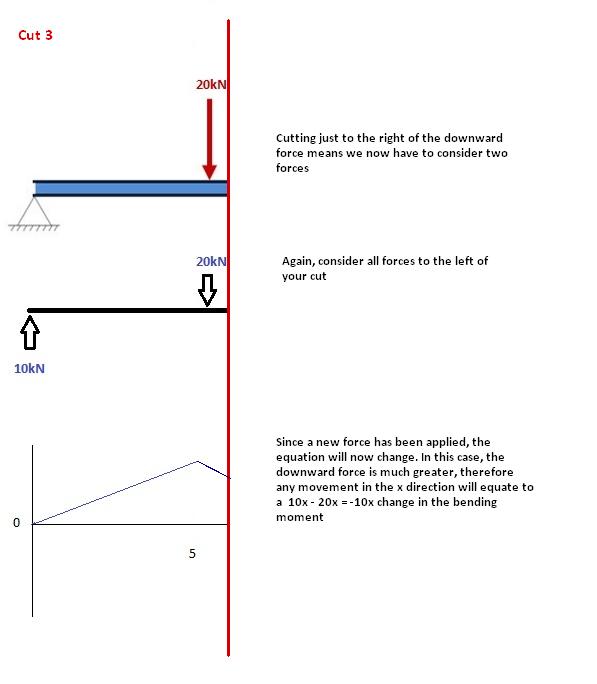
Schnitt 3

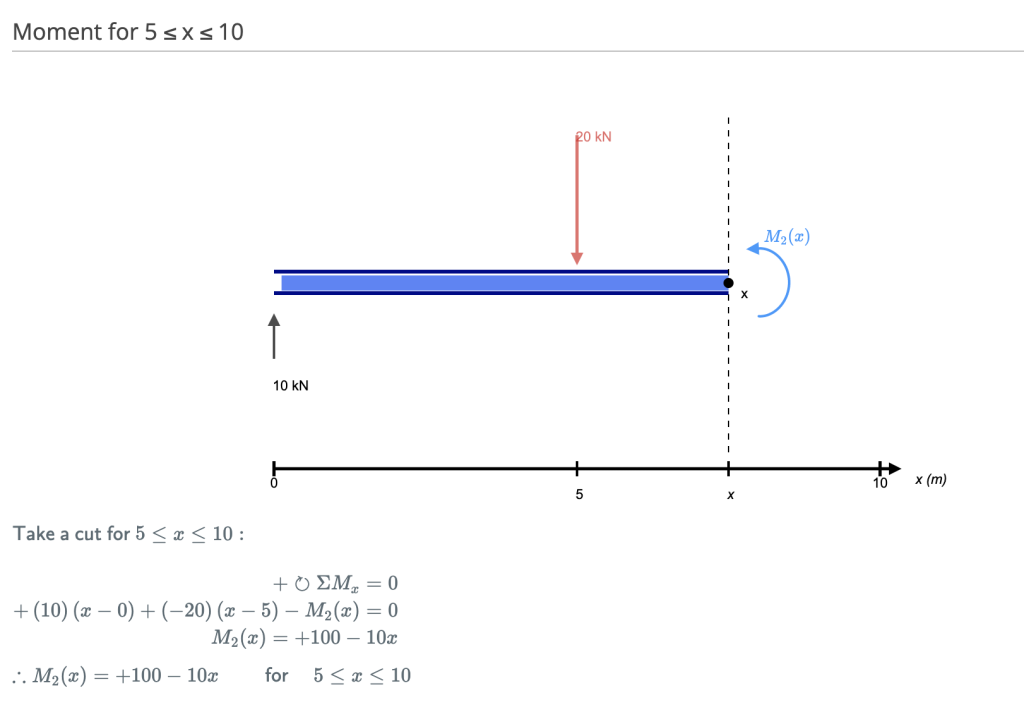
Dieser Schnitt erfolgt direkt nach der zweiten Kraft entlang des Trägers. Jetzt haben wir ZWEI Kräfte, die links von unserem Schnitt wirken: eine 10kN Stützreaktion und eine -20kN nach unten wirkende Last. Wir müssen also beide Kräfte berücksichtigen, wenn wir uns entlang unseres Trägers bewegen. Für jeden Meter, den wir uns über den Träger bewegen, wird ein Moment von +10kNm von der ersten Kraft und -20kNm von der zweiten Kraft hinzugefügt.

Nach dem Punkt x=5 , wird unsere Biegemomentgleichung also zu: M.(x) = 50 +10(x-5) – 20(x-5) M.(x) = 50 -10(x-5) für 5 ≤ x ≤ 10 HINWEIS: Wir schreiben (x-5) weil wir nur den Abstand vom Punkt x=5 wissen wollen. Alles, was vor diesem Punkt liegt, verwendet eine frühere Gleichung.[Quelle: SkyCiv Modul für manuelle Trägerberechnungen]

Schnitt 4

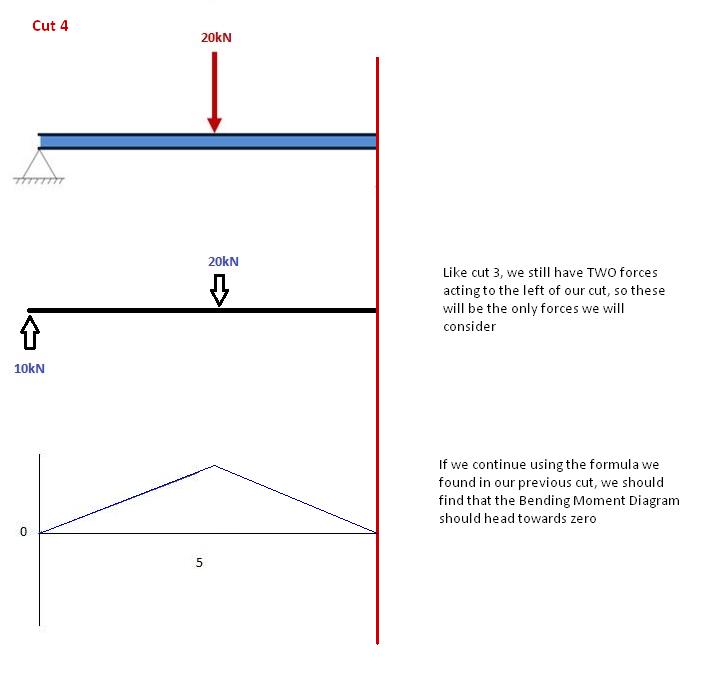
Nochmal, Lassen Sie uns wieder nach rechts zu unserem Träger gehen und einen Schnitt kurz vor der nächsten Kraft mache. In diesem Fall, erfolgt unser nächster Schnitt kurz vor der Reaktion der rechten Stütze. Da zwischen der Stütze und unserem vorherigen Schnitt keine weiteren Kräfte wirken, bleibt die Gleichung gleich, Die Gleichung bleibt gleich: M.(x) = 50 -10(x-5) für 5 ≤ x ≤ 10 Setzen wir x=10 ein, um das Biegemoment am Ende des Trägers zu ermitteln: M.(x) = 50 – 10(10-5) = 0kNm Das macht absolut Sinn. Da unser Träger statisch ist (und nicht rotiert) macht es Sinn, dass unser Träger an diesem Punkt ein Moment von Null hat, wenn wir alle Kräfte berücksichtigen. Damit ist auch eine unserer Ausgangsbedingungen erfüllt, nämlich dass die Summe der Momente am Auflager gleich Null ist. HINWEIS: Wenn Ihre Berechnungen zu einer anderen Zahl als 0, haben Sie einen Fehler gemacht!

Das Endergebnis, wie es in SkyCiv Beam angezeigt wird:

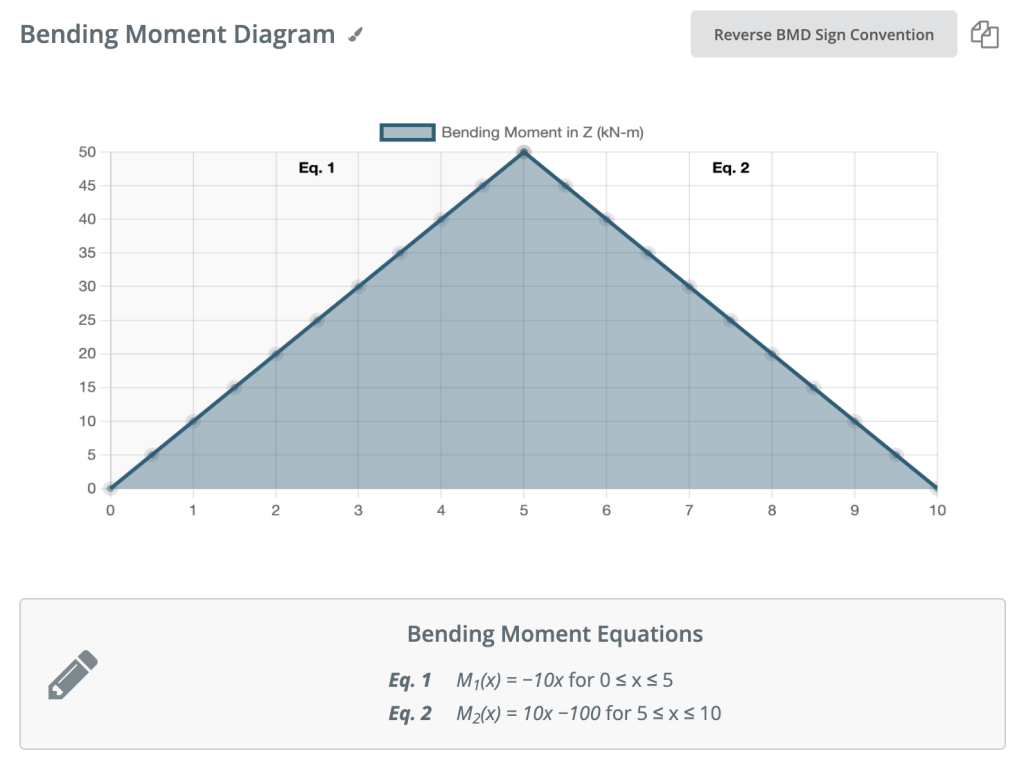
Zeichenkonvention für Biegemomentdiagramme

Wir haben bereits besprochen, wie man Biegemomente bestimmt. Biegemomentendiagramme können hinsichtlich der Vorzeichenkonventionen etwas verwirrend sein. Je nach Quelle kann dasselbe Diagramm in entgegengesetzte Richtungen gezeichnet sein. Die von SkyCiv verwendete Vorzeichenkonvention wird unten angezeigt.

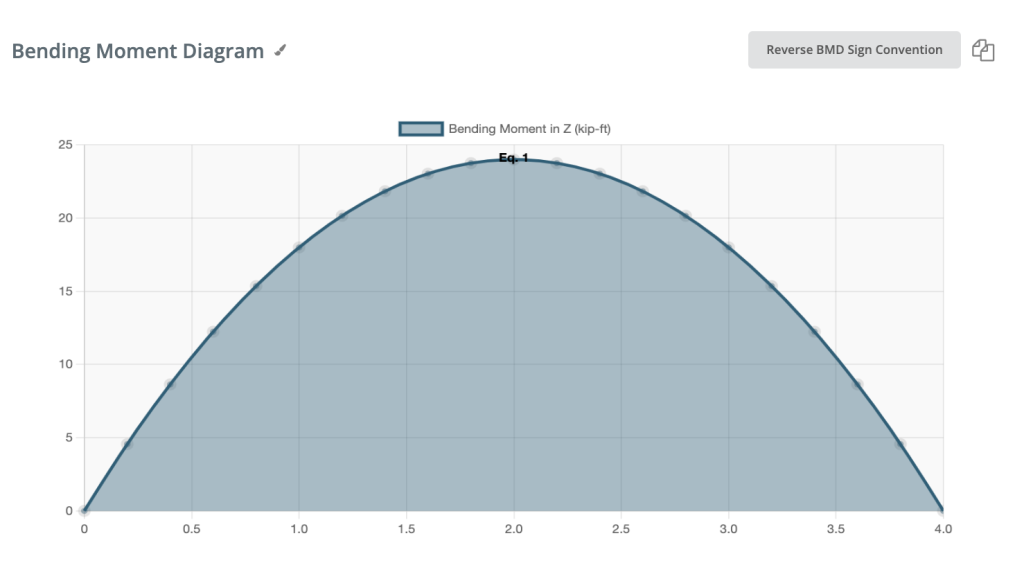
Positives Biegemoment:

Wenn das Biegemoment positiv ist, wird die obere Faser des Trägers zusammengedrückt.

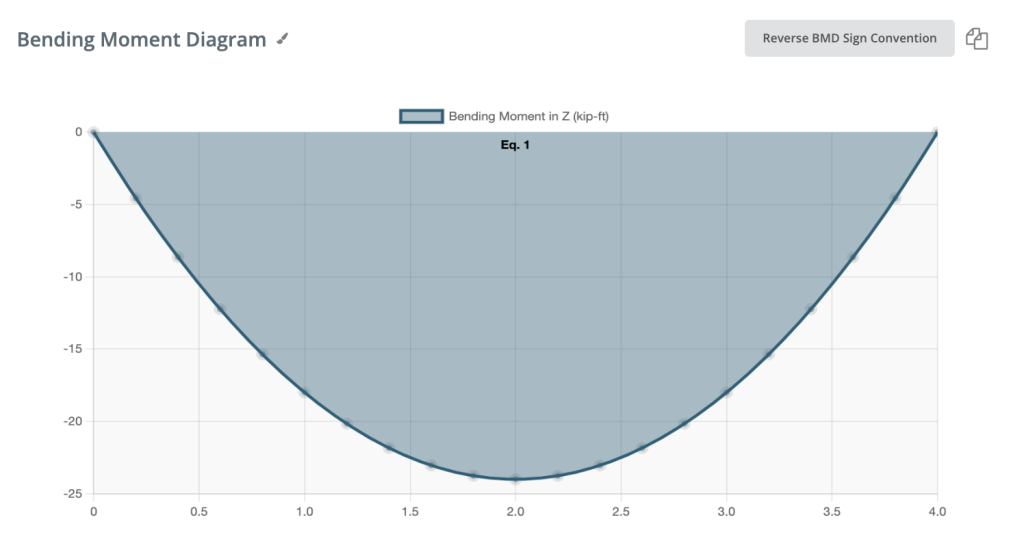
Negatives Biegemoment:

Wenn das Biegemoment negativ ist, wird die untere Faser des Trägers zusammengedrückt.

Dies war ein Leitfaden zur Berechnung von Biegemomentdiagrammen, wenn Sie mehr über dieses Thema erfahren möchten, besuchen Sie unser Beam Tutorials berechnet werden. Hier finden Sie viele weitere hilfreiche Tutorials wie z Biegespannungsformel oder Bestimmen Sie die Reaktionen an den Trägern können.

BONUS: Finden Sie das Biegemoment mit SkyCiv Beam

In unserer kostenpflichtigen Version von SkyCiv Beam zeigt Ihnen der Rechner die vollständigen manuellen Berechnungen und die Schritte zur manuellen Berechnung Ihrer Biegemomentdiagramme an. Modellieren Sie einfach Ihren Träger mit dem Rechner, und klicken Sie auf „Solve“ (Lösen). Der Rechner zeigt Ihnen Schritt für Schritt an, wie Sie ein Biegemomentdiagramm zeichnen (einschließlich Schnitte).