Das Trägheitsmoment ist eine wichtige geometrische Eigenschaft, die im Bauingenieurwesen verwendet wird. Es steht in direktem Zusammenhang mit der Dicke des Querschnitts. Allgemein, Ein höheres Trägheitsmoment impliziert eine größere Festigkeit des Abschnitts, Dies führt zu einer geringeren Durchbiegung bei Belastung. Die Bezeichnung “Trägheitsmoment” ist eigentlich eine weit verbreitete Fehlbezeichnung, da diese Eigenschaft nichts mit Trägheit zu tun hat. Der korrekte technische Name lautet tatsächlich Zweites Flächenmoment. Diese Bezeichnung beschreibt genauer, was diese Eigenschaft misst, Dies kann ungefähr als Maß dafür angesehen werden, wie weit die Fläche des Abschnitts von der neutralen Achse entfernt ist.

Inhaltsverzeichnis

• Trägheitsmoment einer Rechteckformel
• Rechteckige Hohlprofile (RHS)

Trägheitsmoment einer Rechteckformel

Die allgemeine Formel zur Bestimmung des Trägheitsmoments eines Rechtecks ​​lautet:

[Mathematik] ICH_{xx}= dfrac{BD^3}{12} , ICH_{yy}= dfrac{B^3D}{12} [Mathematik]

Bei dem die xx und yy beziehen sich auf die jeweilige Achse, oder Richtung, betrachtet werden.

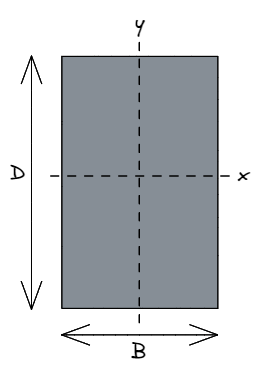
Es ist eine gängige Konstruktionskonvention, die B. bezieht sich auf Breite des Rechtecks, parallel zu einem herkömmlich horizontale x-Achse.

Ähnlich, D. bezieht sich auf Tiefe des Rechtecks, parallel zu einem herkömmlich vertikal y-Achse.

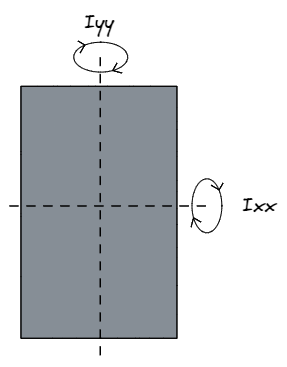
Wenn sich Bauingenieure darauf beziehen Ixx Sie beziehen sich auf die Stärke eines Abschnitts um die x-Achse, Bedeutung in einer Richtung parallel zu der D. Abmessungen, oder y-Achse. Ähnlich, Yyy bezieht sich auf die Stärke um die y-Achse, Bedeutung in einer Richtung parallel zu der B. Abmessungen, oder x-Achse.

Rechteckige Hohlprofile (RHS)

Während Ingenieure beim Entwerfen hypothetisch solide rechteckige Abschnitte verwenden könnten, dies würde eine deutlich größere Menge an Rohmaterial verbrauchen, mit entsprechenden Gewichts- und Kostensteigerungen. Es ist viel üblicher, rechteckige Formen zu verwenden Hohlprofile (gemeinhin als ein bezeichnet RHS). Hier können wir dieselbe Gleichung verwenden, die oben für den allgemeinen rechteckigen Fall definiert wurde, jedoch, wir müssen das Innere subtrahieren hohl Fläche des Rechtecks:

[Mathematik] ICH_{xx}= dfrac{BD^3}{12} – \dfrac{bd^3}{12} [Mathematik]

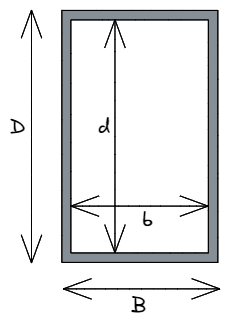
In diesem Fall, Kleinbuchstaben b und d bezeichnen die Größe des hohlen Bereichs innerhalb des Rechtecks, den wir von den äußeren Abmessungen der Form abziehen müssen, Großbuchstaben sein B. und D.. Der Unterschied zwischen jeder entsprechenden Abmessung bezieht sich auf die Dicke des Materials in dieser Abmessung – d.h.. B. – b = Gesamtdicke des Materials parallel zur x-Achse.

Neben den klaren Beispielen für Gewicht und Materialeinsatz, warum werden Hohlprofile oft als mehr bezeichnet effizient als ihre soliden Pendants?

Stellen Sie sich einen Balken vor, der einer vertikalen Belastung nach unten ausgesetzt ist. Wir erwarten, dass die obersten Fasern des Materials einer Druckkraft ausgesetzt werden, während die entsprechenden unteren Fasern einer Zugkraft ausgesetzt werden. Die Fasern entlang der neutralen Achse des Schnitts (parallel zum Schnittmittelpunkt) jedoch, wird weder Druck noch Spannung erfahren, daher der Name neutral Achse.

Wichtig, bleibt die Größe dieser Druck- oder Zugkräfte hängen vom Abstand von dieser neutralen Faser ab – des Materials näher zur neutralen Achse Widerstand leisten muss Weniger Macht.

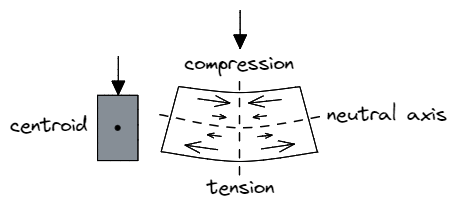
Als Ergebnis, Das Innenmaterial eines massiven Abschnitts widersteht nur einer geringen Krafteinwirkung, während es eine große Fläche einnimmt, da das äußerste Material die größte Belastung trägt! Das Entfernen dieses inneren Teils des Profils und das Hohlmachen verbessert folglich die Effizienz des Abschnitts in Bezug auf sein Gewicht, Kosten, und Materialeinsatz.

Fazit

Zusammenfassend, Die Formel zur Bestimmung des Trägheitsmoments eines Rechtecks ​​lautet Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. Für rechteckige Hohlprofile, Die Formel lautet Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

Das Trägheitsmoment ist sowohl für die Biegemomentkraft/-spannung als auch für die Durchbiegung wichtig. Dies zeigt sich in ihren Formeln, wie in beiden Fällen, I (Trägheitsmoment) steht im Nenner:

Quelle: Biegespannungsformel

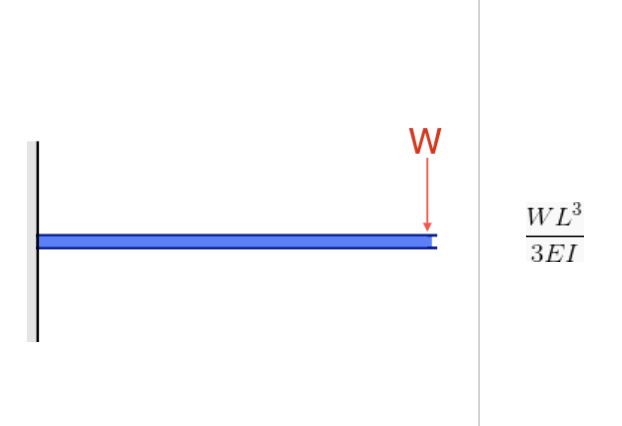
Quelle: Durchbiegungsgleichung in einem freitragenden Balken

Trägheitsmoment-Rechner eines Kreises

Wenn Sie mehr erfahren möchten, Schauen Sie sich unser Tutorial dazu an Trägheitsmoment eines Kreises um zu sehen, wie sich kreisförmige und rechteckige Querschnittsformen vergleichen lassen.

kostenloser Trägheitsmomentrechner