Grundplattenkonstruktion aus Stahl Australisches Codebeispiel
Nachfolgend finden Sie ein Beispiel für einige australische Grundplattenberechnungen, die häufig bei der Grundplattenkonstruktion verwendet werden. Oft beim Entwerfen von Grundplatten, Betrachten wir einige unterschiedliche Prüfungen in Bezug auf die verschiedenen Komponenten einer Grundplatte, nämlich:
- Die Betonbasis – Im Allgemeinen anhand von AS3600 gegen Lager- und Druckkräfte geprüft
- Die Schweißnähte – Schweißnähte müssen überprüft werden, um sicherzustellen, dass sie eine angemessene Rückhaltung bieten und nicht unter Belastung gemäß AS4100 versagen
- Ankerschrauben – kann aus verschiedenen Gründen fehlschlagen, wie unten in den Berechnungsbeispielen für Ankerschrauben gemäß AS5216 gezeigt
- Mitglied aus Stahl (Spalte) prüft – normalerweise basierend auf lokalen Stahlkonstruktionsstandards
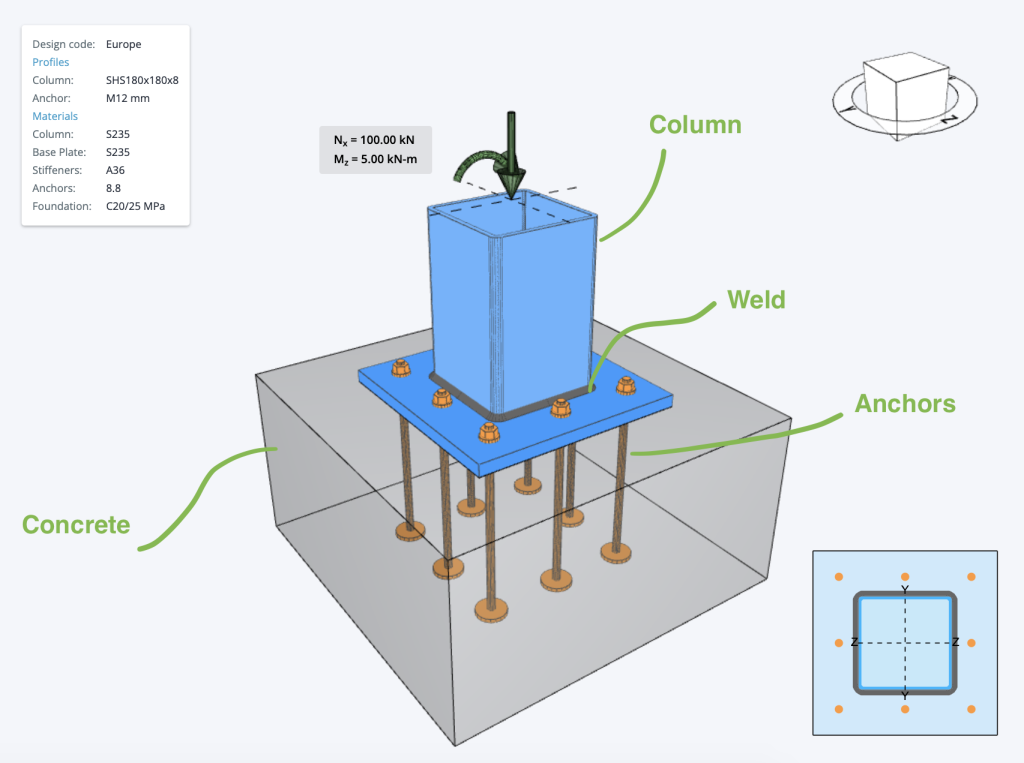
Zur Zeit, bleibt die Design der Grundplatte aus Stahl -Modul implementiert die folgenden Prüfungen unten. Die kostenpflichtige Version dieser Software, enthält detaillierte Schritt-für-Schritt-Berechnungen, damit Ingenieure genau überprüfen können, wie diese Berechnungen durchgeführt werden!
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
Konkreter Check
Mit der Design der Grundplatte aus Stahl prüft Betonlagerprüfung gemäß AS3600-2018 und muss zufrieden stellen:
- \( \phi \) - 0.6 – Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen
- \( f_{c}^{„}\) – Betondruckfestigkeit
- \( EIN_{1}\) – Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen
- \( EIN_{2}\) – Beton (Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen, Stiftung) Flächenmoment
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
Schweißprüfung
Mit der Design der Grundplatte aus Stahl überprüft die gemäß AS4100-2021 entworfene Schweißnaht und muss zufrieden stellen:
- \( \phi \) - 0.80 – Widerstandsfaktor für Schweißverbindungen
- \( f_{Ihre} \) – Nennzugfestigkeit des Schweißgutes
- \( t_{t} \) – Halsdicke entwerfen
- \( v_{w}^{*} \) – Bemessungskraft pro Längeneinheit der Schweißnaht
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
Überprüfung der Ankerbolzen
Mit der Design der Grundplatte aus Stahl Überprüfen Sie die Tragfähigkeit der Anker. Siehe unten Ankerbolzen der Grundplatte gemäß australischem Code:
Schraube in Spannung
Eine Schraube, die der Auslegungszugkraft unterliegt, wird gemäß AS5216 ausgelegt:2018 und soll befriedigen:
- \( \Film_{s} \) – Kapazitätsfaktor für Stahl unter Zug. wo \( \frac{5 \mal f_{ja} }{ 6 \mal f_{uf} } \leq frac{1}{1.4} \)
- \( EIN_{s} \) – Zugspannungsbereich
- \( f_{ja} \) – Mindeststreckgrenze der Schraube
- \( f_{uf} \) – Mindestzugfestigkeit der Schraube
Bolzenschere
Eine Schraube, die einer Bemessungsscherkraft ausgesetzt ist, wird gemäß AS5216 bemessen:2018 und soll befriedigen:
- \( \Film_{s} \) – Kapazitätsfaktor für Stahl unter Zug. wo \( \frac{5 \mal f_{ja} }{ 6 \mal f_{uf} } \leq frac{1}{1.4} \)
- \( EIN_{c} \) – Bereich mit kleinerem Durchmesser der Schrauben
- \( f_{uf} \) – Mindestzugfestigkeit der Schraube
Ankerausbruch
Eine Schraube, die einem Konstruktionsbruch unterliegt, wird gemäß AS5216 konstruiert:2018 und soll befriedigen:
- \( \Film_{c} \) – Tragfähigkeitsfaktor für Ankerversagensarten in Verbindung mit Beton \)
- \( N_{Rk,c}^{Das} \) – Charakteristische Festigkeit eines Verbindungselements, entfernt von den Auswirkungen benachbarter Befestigungsmittel oder Kanten des Betonbauteils.
- \( N_{tf,G}^{*} \) – Summe der Zugkräfte von Ankern mit gemeinsamer Betonausbruchkegelfläche.
- \( EIN_{c,N.} \) – Betonausbruchkegelbereich für Ankergruppe.
- \( EIN_{c,N.}^{Das} \) – Betonausbruchkegelbereich für Einzeldübel nicht durch Kanten beeinflusst.
- \( \phi_{s,N.} \) – Parameter in Bezug auf die Spannungsverteilung im Beton aufgrund der Nähe des Befestigungselements zu einer Kante des Betonbauteils.
- \( \phi_{Ausbruchkegelbereich für Einzeldübel nicht durch Kanten beeinflusst,N.} \) – Ausbruchkegelbereich für Einzeldübel nicht durch Kanten beeinflusst.
- \( \phi_{ec,N.} \) – Modifikationsfaktor für exzentrisch auf Zug belastete Ankergruppen.
- \( \phi_{M.,N.} \) – Parameter, der die Wirkung einer Druckkraft zwischen Anbauteil und Beton berücksichtigt.
Betonausbruchkontrolle
Eine Schraube, die der Auslegungszugkraft unterliegt, wird gemäß AS5216 ausgelegt:2018 und soll befriedigen:
- \( \Film_{c} \) – Tragfähigkeitsfaktor für Ankerversagensarten in Verbindung mit Beton \)
- \( k_{s} \) – Im Bewertungsbericht veröffentlichter Parameter
- \( N_{Rk,c} \) – Charakteristische Betonkonusfestigkeit für ein einzelnes Befestigungselement oder Befestigungselement in einer Gruppe
Überprüfung des Nutzenverhältnisses von Ankerbolzen
Nutzwertverhältnis für Stahl
Wechselwirkung von Zug- und Scherkräften von Stahl
Nutzwert für Beton
Wechselwirkung von Zug- und Querkräften im Beton


