Das Trägheitsmoment ist eine wichtige geometrische Eigenschaft, die in der Bautechnik verwendet wird, da es direkt mit der Menge zusammenhängt des Materials Stärke deine Sektion hat. Im Allgemeinen gilt, Je höher das Flächenträgheitsmoment, je mehr Festigkeit es hat und desto weniger verbiegt es sich unter Last. Das Trägheitsmoment eines Kreises, oder irgendeine Form für diese Angelegenheit, ist im Wesentlichen, wie viel Drehmoment erforderlich ist, um die Masse um eine Achse zu drehen – daher das Wort Trägheitsmoment in seinem Namen. Hinweis, dies ist nicht zu verwechseln mit der Momentenfläche der Trägheit (Zweites Trägheitsmoment) was eine ganz andere Berechnung und ein ganz anderer Wert ist.

Trägheitsmoment einer Kreisformel

Eine weitere nützliche Übung besteht darin, sich dies alles anhand der allgemeinen Kreisformel des Trägheitsmoments anzusehen:

[Mathematik] ICH_{x}, ICH_{j}= dfrac{\Pi}{64}D^4 [Mathematik]

Und die Formel für das Trägheitsmoment für hohle Kreisprofile:

[Mathematik] ICH_{x}, ICH_{j}= dfrac{\Pi}{64}D^4 – \dfrac{\Pi}{64}d^4 [Mathematik]

Offensichtlich, Wir können sehen, dass ein Teil des Trägheitsmoments aus dem Ausschnitt entfernt wird. Jedoch, weil dies nicht viel Rückhalt gegen Biegung bietet (da es so nah am Schwerpunkt liegt), es ist ein ineffizienter Materialeinsatz. Das Entfernen dieses Teils des Abschnitts verbessert also tatsächlich die Effizienz des Abschnitts.

Trägheitsmoment eines Kreises – Eine detaillierte Aufschlüsselung

Die Momententrägheit ist sowohl für die Biegemomentkraft/-spannung als auch für die Durchbiegung wichtig. Dies ist offensichtlich, wenn man ihre Formel betrachtet, wobei in beiden Fällen, I (Trägheitsmoment) steht im Nenner:

Quelle: Biegespannungsformel

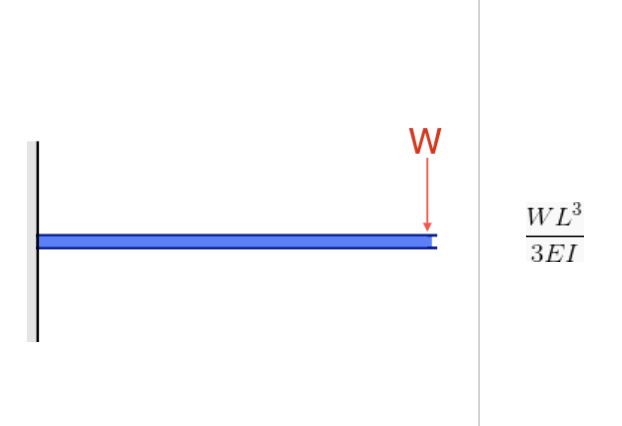
Quelle: Durchbiegungsgleichung in einem freitragenden Balken

Das Trägheitsmoment in kreisförmigen Querschnitten hat ein besonderes Verhalten. Erstens, sie haben in beiden Achsen das gleiche Trägheitsmoment (bekannt als große und kleine Achse). Dies ist sinnvoll, da der Schnitt sowohl in X- als auch in Y-Richtung symmetrisch ist. Wir werden uns ansehen, dass dies bei anderen nicht immer der Fall ist Querschnitte, wenn wir unten mit einem I-Beam vergleichen. Jedoch, Dies kann von Vorteil sein, wenn die Belastung nicht immer entlang der starken Achse des Stabs erfolgt, da Sie die Festigkeit des Stabes unabhängig von der Lastrichtung vorhersagen können. Trotz dieses, kreisförmige Querschnitte haben normalerweise keine sehr hohen Trägheitsmomentwerte für ihr Gewicht (im Vergleich zu einem I-Beam zum Beispiel) wie wir in der nächsten Sitzung mehr erfahren werden.

Vor- und Nachteile von Rundschreiben

Es ist interessant, das Trägheitsmoment eines Kreises mit anderen Formen zu vergleichen, um wirklich zu verstehen, wie es sich anders verhält. Für einen, Der größte Teil der Masse konzentriert sich um die den Schwerpunkt, mit nicht so viel Masse oben und unten. Dies ist ziemlich wichtig für Trägheitsmomentberechnungen, denn je weiter weg die masse, je höher der Wert. Schauen wir uns einen Vergleich an, produziert von SkyCiv Section Builder:

Trägheitsmomentrechner

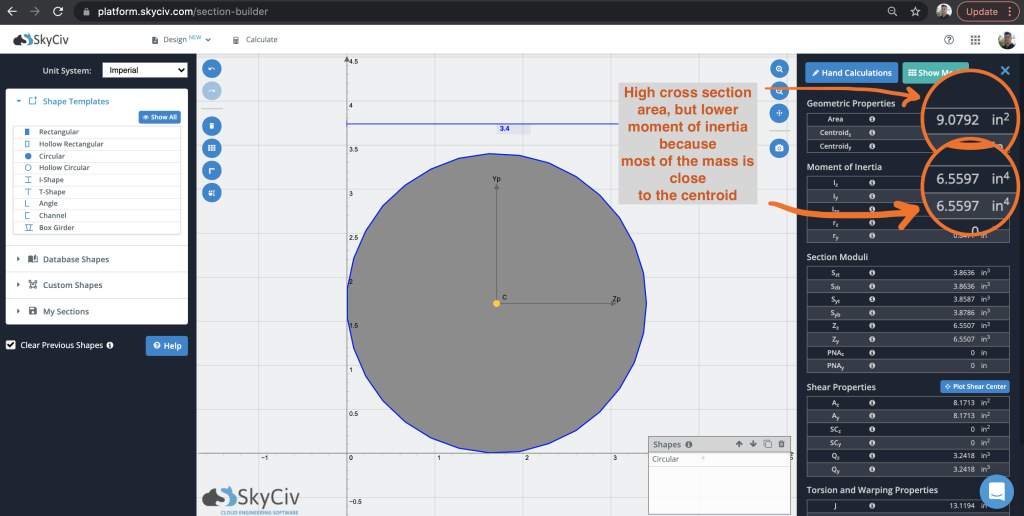
Also oben, wir haben ungefähr 9 Quadratzoll Material mit einem Trägheitsmoment von 6.5597. Wir können auch sehen, dass die Werte Iy und Iz gleich sind, da der Schnitt in beide Richtungen symmetrisch ist, wie vorab erwähnt. Beim Vergleich mit einem I-Beam mit der gleichen Fläche, Wir können den Unterschied sehen, dass wir den größten Teil unserer Masse haben weiter weg vom Schwerpunkt:

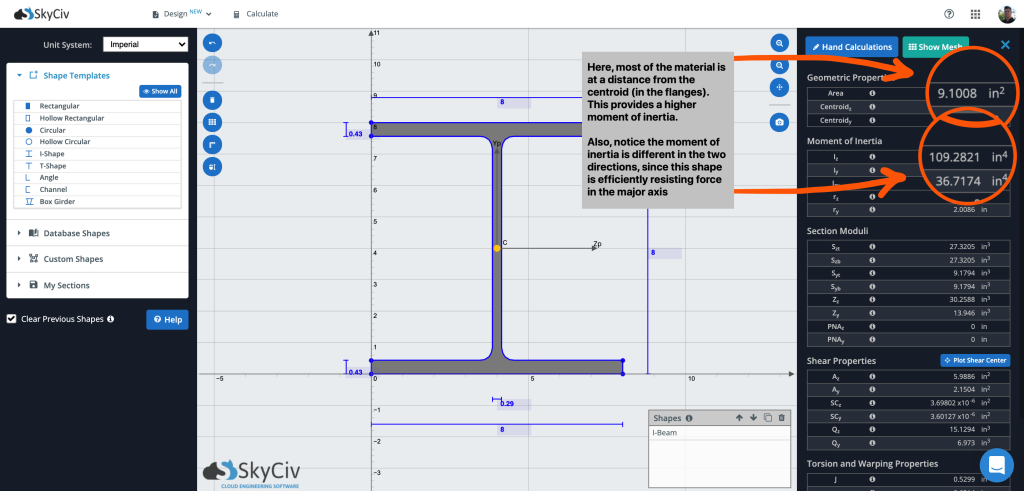
Trägheitsmoment eines hohlen kreisförmigen Abschnitts

Angesichts dieses Verhaltens, Aus diesem Grund sehen wir im Hochbau oft nicht viele massive Kreisprofile und werden oft durch günstigere ersetzt Hohlkreis Querschnitte. Diese sind effizienter bei der Bereitstellung höherer Trägheitsmomentwerte aus dem gleichen Grund wie der I-Träger: der größte Teil der Masse ist vom Schwerpunkt entfernt. Stellen Sie sich eine hohle kreisförmige Form mit einer ähnlichen Fläche vor:

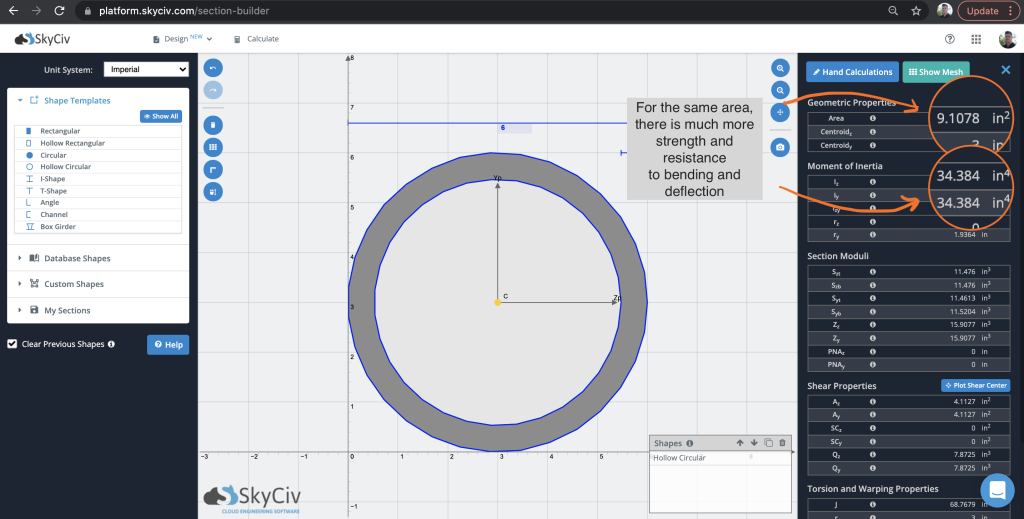
So, zusammenfassend für das gleiche Material wie ein massiver Kreisquerschnitt, das Trägheitsmoment ist vorbei 5 mal stärker. Dies spielt eine entscheidende Rolle bei der Festigkeit gegen Biegemomentkraft und Durchbiegung.