Definition von Frequenzanalyse?
Beim Entwerfen von Gebäuden, es gibt zwei Arten von Lasten berücksichtigen: statisch und dynamisch. Für den ersten, es ist nur erforderlich, die direkte Reaktion der Struktur auf die aufgebrachten permanenten Lasten in Form von Verschiebungen und Spannungen zu berechnen. Dies kann mit der Steifigkeits- oder der Finite-Elemente-Methode erreicht werden.
Bei dynamischer Analyse, es ist schwieriger, den Bereich möglicher Schwankungen in der Reaktion der Struktur aufgrund zeitabhängiger Lasten zu berücksichtigen. Deshalb, Einige neue Tools oder Funktionen müssen unbedingt in die Analyse aufgenommen werden. So, Frequenzanalyse, eine grundlegende Methode in der Schwingungsmechanik, entsteht.
Dieses Verfahren erhält die zeitliche Änderung der Strukturbewegung aufgrund der aufgebrachten dynamischen Lasten. Genauer, dies impliziert die Verwendung der natürlichen Schwingungseigenschaften des Tragwerks zur Berechnung der inneren Kräfte, Verschiebungen, Stabilitätsprobleme, etc.
Weitere Informationen zum Thema, Wir empfehlen, einen SkyCiv-Artikel zu lesen, der kurz erklärt, wie man a durchführt Dynamische Frequenzanalyse mit SkyCiv Strukturanalyse-Software.
Warum ist die Frequenzanalyse designrelevant?
Der beste Weg, die Bedeutung der Frequenzanalyse in einem Design zu messen, besteht darin, den Fall einiger Strukturen zu beobachten, die aufgrund eines schlechten dynamischen Verhaltens ausgefallen sind. Eine berühmte Brücke in Nordamerika ist die Tacoma Narrows, die schließlich nach windinduzierten anhaltenden periodischen Vibrationen zusammenbrach. Die folgenden Bilder zeigen die zunehmende Verschiebung entlang der Brücke kurz vor dem Einsturz, konzentrierte sich hauptsächlich auf die Fahrbahn:

Abbildung i. Laterale Torsionsschwingungen in der Tacoma Narrows Bridge

Abbildung ii. Erhöhte Verschiebung auf der Brücke vor dem Einsturz.

Abbildung iii. Katastrophaler Brückeneinsturz
In dieser Fallstudie, Eine ordnungsgemäße Frequenzanalyse wurde nicht durchgeführt und die Struktur wurde nicht angemessen entworfen, um die Eigenfrequenz der Struktur zu berücksichtigen.
Einfaches Pendel
Die Frequenzanalyse untersucht die unterschiedlichen Formen, die eine Struktur entwickelt, wenn sie externen dynamischen Einwirkungen ausgesetzt ist. Aus diesem Grund erhalten Sie mehrere verschiedene Modi. Dann verwenden Sie diese Formulare, Wir können die Elementgrößen der Struktur durch die Schnittgrößen ermitteln, die erforderlich sind, um das Gleichgewicht zu gewährleisten.
Bevor wir tiefer in die technischen und mathematischen Überlegungen zur Frequenzanalyse einsteigen, Überprüfen Sie das nächste einfache System einer Pendelsäule, das in Abbildung iv gezeigt wird.
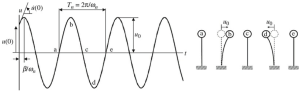
Abbildung iv. Das dynamische Verhalten eines frei schwingenden Pendelsystems
Verwenden einer einfachen Analyse, wie im letzten Bild angegeben, wir können die Bewegung der oberen Masse für die Pendelsäule jedes Mal definieren. Das Hauptziel dieses Artikels wird es sein, die Häufigkeitsanalyse für zwei typische Fälle zu behandeln, einzelne und mehrere Freiheitsgrade.
Einzelner Freiheitsgrad
Dieser spezielle Fall ist der einfachste für die dynamische Analyse. Das Verhalten wird mit dem Gleichgewichtsgesetz von D’Alembert beschrieben, eine Erweiterung des zweiten Newtonschen Gesetzes.
Die folgende Abbildung zeigt die Elemente des SDOF-Systems, Steifheit (k), Dämpfung (c), und Massenquelle ( Mio.) für Trägheitskräfte. Die zeitveränderliche externe Kraft, die auf die Masse ausgeübt wird, wird durch dargestellt \({p(t)}\).
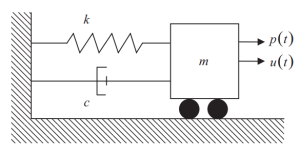
Abbildung 1. Einzelner Freiheitsgrad (SDOF) System. (Schüssel, 2017, seite 56)
Alle Elemente müssen die dynamische Gleichgewichtsbedingung erfüllen:
\({ Mio.}{\Punkt{u}}+{c}{\Punkt{u}}+{k}{u}={p(t)}\)
Dies ist eine lineare Differentialgleichung zweiter Ordnung, und seine Lösung besteht aus zwei Komponenten:
\({u(t)}={u}_{h}(t)+{u}_{p}(t)\)
Wo:
- \({u(t)}\) ist die absolute Verschiebung.
- \({u}_{h}(t)\) ist die homogene Lösung, im Allgemeinen mit dem Fall der freien Schwingung.
- \({u}_{p}(t)\) ist die spezielle Lösung gemäß der angelegten Erregung.
Wir konzentrieren uns nur auf die homogene Lösung zur Beschreibung des Schwingungsverhaltens und der kritischsten dynamischen Eigenschaften einer Struktur.
Lassen Sie uns die folgenden Begriffe definieren:
\({\Omega_{n}}={\sqrt(\frac {k}{ Mio.})}\) Winkelfrequenz
\({\xi}={\frac{c}{{2}{ Mio.}{\omega_n}}}={\frac{c}{{2}{\sqrt(\frac {k}{ Mio.})}}}\) Bruchteil der kritischen Dämpfung
Wenn der Anteil der kritischen Dämpfung kleiner ist als 1, das Vibrationsgehäuse wird unterdämpft; das ist, Es werden abgeschlossene Zyklen ausgeführt, bevor die Bewegung stoppt.
Die Lösung hat die folgende allgemeine Form
\({äh}={e^{{-\xi}{\Omega_{n}}{t}}}{[{Ein}{cos}{\omega_d}{t}+{B.}{ohne}{\omega_d}{t}]}\)
Wo:
- A und B sind Integrationskonstanten, die von den Anfangsbedingungen der Bewegung abhängen.
- \({\omega_d}={\omega_n}{\sqrt({{1}-{\xi^2}})}\) ist die gedämpfte Winkelfrequenz
Einmal Auswertung der Konstanten A und B, die allgemeine Lösung für den ungedämpften Fall ist
\({äh}={e^{{-\xi}{\Omega_{n}}{t}}}{[{u_0}{cos}{\omega_d}{t}+{\frac{{\Punkt{u_0}}+{\xi}{\omega_n}{u_0}}{\omega_d}}{ohne}{\omega_d}{t}]}\)
Wo:
- \({u_0}\) ist die anfängliche Massenverschiebung
- \(\Punkt{u_0}\) ist die Massenanfangsgeschwindigkeit
Wenn wir die Lösung mit einigen Werten der Anfangsbedingungen darstellen, wir erhalten die folgende Figur.
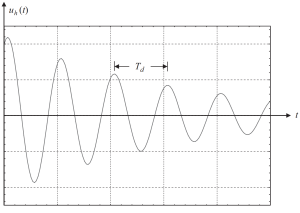
Abbildung 2. Die Verschiebung führt zu einem homogenen Teil der Lösung in einem unterkritisch gedämpften Fall. (Schüssel, 2017, seite 58)
Im anderen Fall, Es ist entscheidend zu analysieren, was passiert, wenn der Anteil der kritischen Dämpfung einen Wert von hat 1. \({\xi}=1). Dieser Zustand impliziert eine Struktur mit vollständiger Dämpfung.
Die zu verwendende Gleichung ist
\({äh}={e^{{-\Omega_{n}}{t}}}{\{u_0+({\Punkt{u_0}}+{\omega_n}{u_0}){t}}\}\)
Und ihr Diagramm, das verschiedene Fälle von Anfangsbedingungen zeigt, ist im folgenden Bild zu sehen.
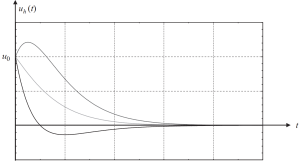
Abbildung 3. Die Verschiebung führt zu einem homogenen Teil der Lösung in einem kritisch gedämpften Fall. (Schüssel, 2017, seite 58)
Reaktionsparameter
Der vorherige Abschnitt hat uns geholfen, die Lösung für freie dynamische Schwingungen in einem SDOF-System zu definieren. Die beiden Hauptparameter sind die Eigenfrequenz \(\omega_n\) was angibt, wie die Struktur selbst schwingen wird, und der Anteil der kritischen Dämpfung \(\xi), die die Geschwindigkeit in abklingenden Schwingungen definiert.
Allgemein, Strukturen haben eine geringe Dämpfung mit einem Maximalwert von \(\xi)=10 %. Bewerten wir mit diesem Wert die gedämpfte Eigenfrequenz, Das Ergebnis ist \({\omega_d}=0,995{\omega_n}\). So, Es wird empfohlen, es zu verwenden \({\omega_d}{\dickca}{\omega_n}\).
Wir können die dynamischen Eigenschaften in der folgenden Tabelle zusammenfassen.
| Winkelfrequenz (rad/s) | Eigenfrequenz (Hz) | Natürliche Periode (s) | |
|---|---|---|---|
| Winkelfrequenz \({\omega_n}\) | \({\omega_n}\) | \(2{\Pi}{f_n}\) | \(\frac{2{\Pi}}{T_n}\) |
| Eigenfrequenz \({f_n}\) | \(\frac{\omega_n}{2{\Pi}}\) | \(f_n\) | \(\frac{1}{T_n}\) |
| Natürliche Periode \({T_n}\) | \(\frac{2{\Pi}}{\omega_n}\) | \(\frac{1}{f_n}\) | \(T_n\) |
Tabelle 1. Beziehung zwischen Kreisfrequenz, Eigenfrequenz, und Punkt (Schüssel, 2017, seite 60)
Mehrere Freiheitsgrade
Wenn viele Massen in einer Struktur vorhanden sind, wir müssen mehrere Koordinaten definieren, um die Position dieser Massen jederzeit zu beschreiben. Ein besonderes und offensichtliches Beispiel ist in der folgenden Abbildung dargestellt, bestehend aus einem komplexen Pendel, bei dem verschiedene Winkel benötigt werden, um die Position in jedem Moment der Bewegung festzulegen.
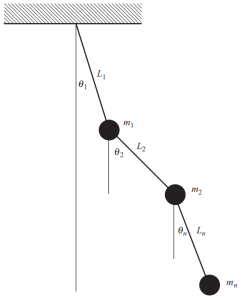
Abbildung 4. Pendel mit mehreren Massen. (Schüssel, 2017, seite 53)
In diesem Abschnitt, Wir analysieren Strukturen’ allgemeine dynamische Reaktion unter Verwendung der Erweiterung der Eigenschaften Frequenzanalyse für mehrere Freiheitsgrade.
Es ist zwingend erforderlich, sich des Modellierungsprozesses bewusst zu sein, wenn es um eine tatsächliche Struktur geht. Die folgenden Bilder beschreiben die erforderlichen Schritte zum Erstellen eines mathematischen Modells, das bereit ist, die Frequenzanalyse anzuwenden, um seine dynamische Reaktion zu beschreiben.
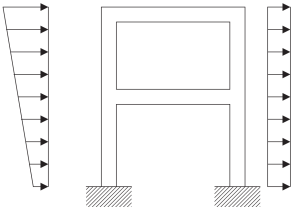
Abbildung 5. Physikalisches Modell eines Kontinuumsstrukturrahmens. (Schüssel, 2017, seite 23)
Der erste Schritt besteht darin, Massen an jedem Schnittpunkt von Trägern und Stützen auf einer Ebene zusammenzufassen. Jeder Knoten hat drei mögliche Bewegungen, zwei lineare Verschiebungen, und eine Drehung. Konsequent in der Analyse sein, Massen und polare Trägheitseigenschaften müssen berücksichtigt werden.
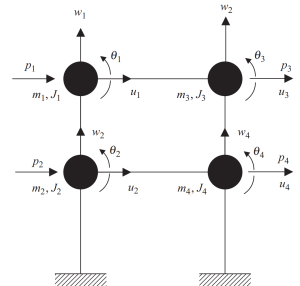
Abbildung 6. Konzentrierte Massen an Knoten mit Verschiebungs- und Rotationsfreiheitsgraden. Diskretes System. (Schüssel, 2017, seite 23)
Die Methode der statischen Kondensation kann dazu beitragen, die Komplexität der Analyse zu reduzieren, Vernachlässigung von Rotations- und Translationsträgheit.
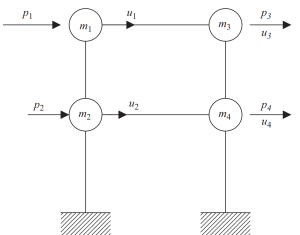
Abbildung 7. Statische Verdichtung des Freiheitsgrades auf nur horizontale Verschiebung. (Schüssel, 2017, seite 23)
Im letzten Schritt, Wir können die horizontale Bewegung für dieses Frame-Beispiel in nur zwei Knoten zusammenfassen.
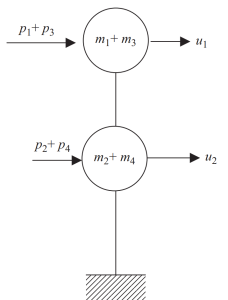
Abbildung 8. Endgültige statische Verdichtung auf zwei Knoten und Freiheitsgrad der horizontalen Verschiebung. (Schüssel, 2017, seite 24)
Wie wir es im vorherigen Abschnitt mit dem SDOF-System getan haben, Wir werden die Lösung der Bewegungsgleichung für mehrere Freiheitsgrade entwickeln.
Die Bewegungsgleichung schreibt in Matrixform als
\([M.]\{\Punkt{u}\} + [C.]\{\Punkt{u}\}+[K.]\{u\}={p(t)}\)
Wo:
- \([M.]\) ist die Massenmatrix
- \([C.]\) ist die Dämpfungsmatrix von Coulumb
- \([K.]\) ist der Steifigkeitsmatrix
Wir müssen die freie Schwingungslösung untersuchen, um die Antwortparameter zu erhalten. Es wird keine Dämpfung und Kraft auf das System ausgeübt, Es werden nur die Anfangsbedingungen ausgewertet.
\([M.]\{\Punkt{u}\} +[K.]\{u\}={0}\)
Analog zum ersten Fall für eine SDOF, wir können eine sinusförmige Lösung der Form testen.
\({u(t)}={\phi}{({ein}{cos}{\Omega}{t}+{b}{ohne}{\Omega}{t})}\)
\({\Punkt{u}{(t)}}={-{\Omega}^ 2}{\phi}{({ein}{cos}{\Omega}{t}+{b}{ohne}{\Omega}{t})}\)
In dem der Vektor \(\Phi) ist ein Formvektor, der nicht zeitabhängig ist. Die Koeffizienten “ein” und “b” sind Konstanten, die man erhält, wenn man Anfangsbedingungen auswertet.
Nach dem Einsetzen beider Ausdrücke für die Testlösung in die Bewegungsgleichung, wir erhalten das lineare Eigenwert-Eigenvektor-Problem:
\([K.]{\phi}={{\Omega}^ 2}[M.]{\phi}\)
Wo:
- \({{\Omega}^ 2}\) ist die Menge der Eigenwerte
- \({\phi}\) ist die Menge der Eigenvektoren
Die Lösung dieses klassischen Problems für das Rahmenbeispiel in den neuesten Abbildungen zeigt, wie Massen schwingen werden. Das bedeutet, dass sich jede Masse entsprechend dem Wert der Eigenvektoren in horizontaler Richtung bewegt.
Sehen Sie sich das folgende Bild dieses Verhaltens an.
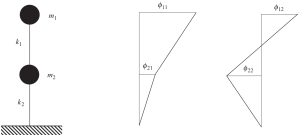
Abbildung Nr.9. Frequenzanalyse, die die Ergebnisse der beiden Eigenvektoren zeigt. (Schüssel, 2017, Seite 135)
SkyCiv Structural 3D
Führen Sie Frequenzanalysen für Ihre Strukturen durch SkyCiv Structural 3D. Melden Sie sich noch heute an, um loszulegen!
Verweise:
- Eduard Kausel, (2017). “Fortgeschrittene Strukturdynamik” 1st. Auflage, Cambridge University Press


