Ein Leitfaden zur statischen Determination, Unbestimmtheit, und Instabilität

Sobald die Struktur vollständig modelliert ist und die Lasten aufgebracht sind, Es ist Zeit, das System zu lösen, um alle Ergebnisse zu finden, die aus der Analysephase stammen: Reaktionen, interne Kräfte (Querkraft, Biegemoment, Axialkraft, und Torsion), Verschiebungen, und betont. Manchmal laufen die Dinge nicht wie erwartet und wenn es um die Lösung geht, Möglicherweise erhalten Sie eine lästige Meldung “Lösung fehlgeschlagen! Überprüfen Sie Ihre Struktur eingerichtet, da das Modell wahrscheinlich instabil ist”, und die Chancen stehen gut, dass Sie nicht genau wissen, was mit dem Modell nicht stimmt. Dieser Artikel erklärt das Konzept der strukturellen Stabilität zusammen mit statischer Bestimmtheit und Unbestimmtheit, die sehr verwandte Themen sind, Es enthält auch einige Tipps zur Fehlerbehebung bei einem instabilen Modell.

Im Allgemeinen, Eine Struktur gilt als innerlich stabil, wenn sie ihre Form behält, wenn Stützen entfernt werden. Umgekehrt, Eine Struktur gilt als innerlich instabil, wenn sie sich einmal von den Stützen gelöst hat, Die Struktur kann ihre Form nicht beibehalten und kann große Verschiebungen erfahren oder sogar zusammenbrechen. Das gesagt, Wir werden uns die statische Bestimmtheitsformel genauer ansehen, sowohl für innerlich instabile als auch für stabile Strukturen. Die statische Bestimmtheitsformel hilft, eine Struktur als äußerlich instabil zu klassifizieren, statisch bestimmt, oder statisch unbestimmt.

Statische Bestimmtheit innerlich stabiler Strukturen

Ein intern stabiles Tragwerk kann als extern statisch bestimmt angesehen werden, wenn alle seine Lagerreaktionen durch Lösung der Gleichgewichtsgleichungen gelöst werden können. Für ebene Strukturen unter Lasten in der Ebene, es müssen drei unterstützende Reaktionen vorhanden sein, damit die Struktur im Gleichgewicht ist. zusätzlich, da nur drei Gleichgewichtsgleichungen zur Verfügung stehen, höchstens drei Reaktionen sind zu finden, also sollte es genau drei Reaktionen geben, die die Ebenenstruktur unterstützen. Einige Beispiele für äußerlich statisch bestimmte flächige Strukturen sind im folgenden Bild dargestellt:

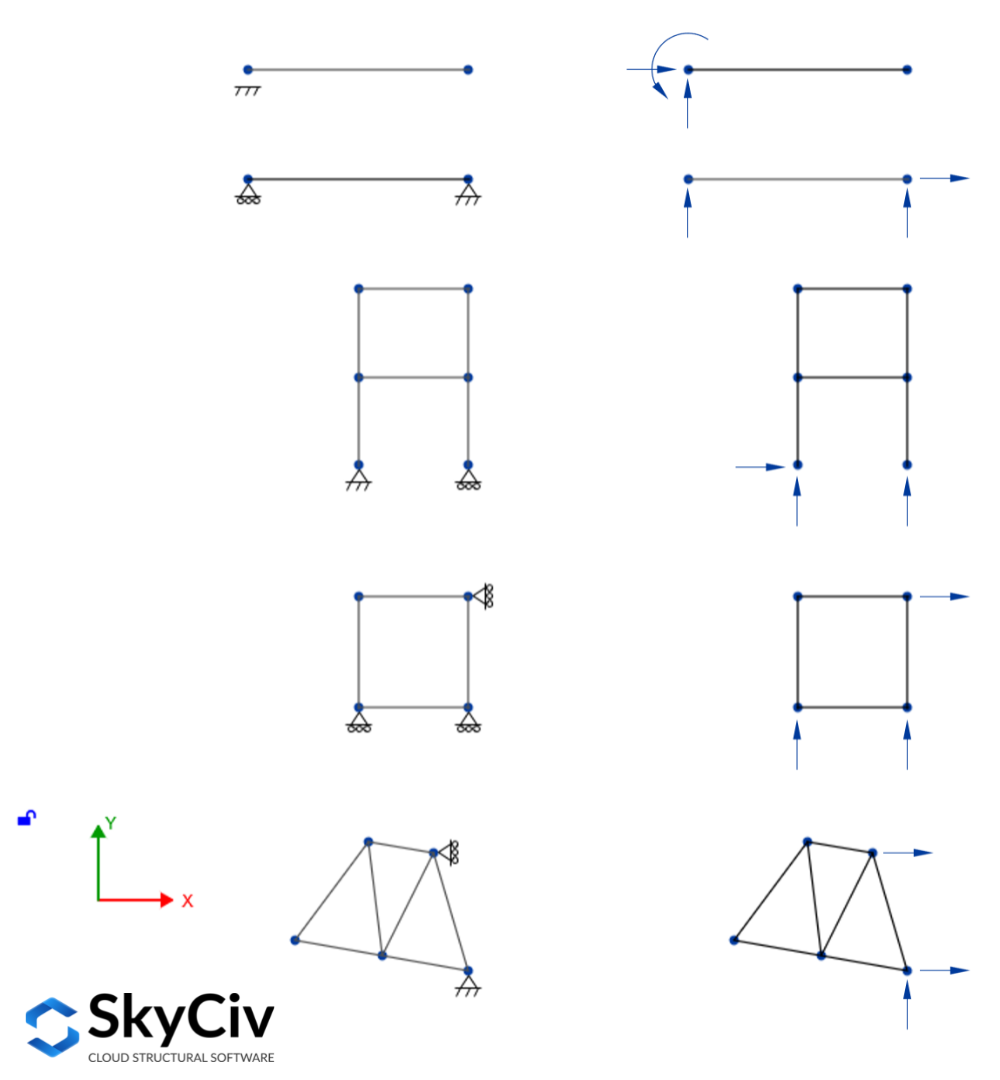
Wenn mehr als drei Reaktionen die Struktur unterstützen, es wird eine statisch unbestimmte äußere Struktur genannt, da es nicht möglich ist, alle Reaktionen mit den drei Gleichgewichtsgleichungen zu lösen. Diese Reaktionen werden als externe Redundanz bezeichnet, und die Anzahl der externen Redundanzen ist als Grad der externen Unbestimmtheit bekannt, Als Gleichung geschrieben sieht das so aus:

\(i_e = r – 3\)

Wo \(R) ist die Anzahl der Reaktionen, die die Struktur unterstützen.

In den Fällen, in denen die Struktur durch weniger als drei Stützreaktionen gestützt wird, diese reichen nicht aus, um zu verhindern, dass sich die Struktur auf ihrer Ebene bewegt, Da diese Struktur unter einem allgemeinen Lastsystem nicht im Gleichgewicht bleiben würde, wird sie als extern statisch instabil bezeichnet. Basierend auf der Anzahl der Reaktionen \(R), es ist möglich, die statische Bestimmtheit zu bestimmen, Unbestimmtheit, und Instabilität von intern stabilen Strukturen unter Verwendung der folgenden Kriterien:

\( r begin{Fälle} < 3, \; \textrm{statisch instabile äußere Struktur} \\ = 3, \; \textrm{statisch bestimmte äußere Struktur} \\ > 3, \; \textrm{statisch unbestimmte äußere Struktur} \Ende{Fälle}\)

Es ist wichtig zu erwähnen, dass sobald die letzten beiden Bedingungen erfüllt sind, Es ist nicht gewährleistet, dass die Struktur stabil ist. Dies bedeutet, dass selbst wenn die Struktur von mehr als drei Reaktionen gestützt wird, wenn Stützen und nicht richtig angeordnet sind, die Struktur immer noch instabil sein kann. Dies wird als geometrische externe Instabilität bezeichnet und wird durch zwei Hauptgründe verursacht:

• Bei all den Reaktionen’ Die Wirkungslinien sind parallel, da die Struktur nicht daran gehindert wird, sich in die senkrechte Richtung der Reaktionen zu verschieben
• Bei all den Reaktionen’ Aktionslinien sind an einem Punkt gleichzeitig, da die Struktur um den Parallelitätspunkt rotieren darf

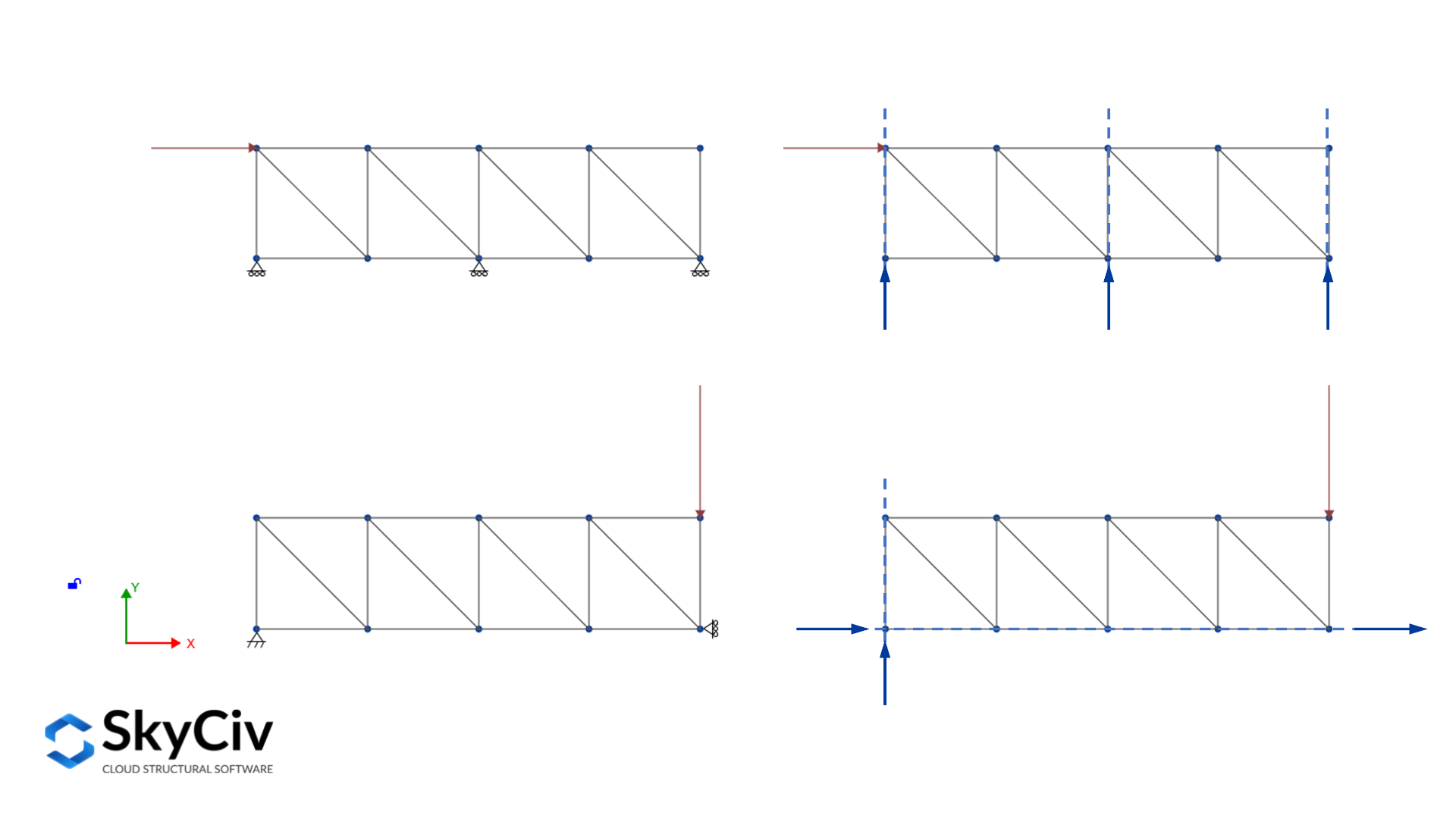
Statische Bestimmtheit innerlich instabiler Strukturen

Intern instabile Strukturen sind solche, die, wenn sie von den Stützen gelöst werden, ihre ursprüngliche Form nicht beibehalten können. Ohne Stützen, die Glieder der Struktur würden große Verschiebungen gegeneinander erfahren. Um die statische Bestimmtheit zu definieren, Unbestimmtheit, und externe Stabilität dieser Strukturen, Die Gleichungen ändern sich aufgrund der zusätzlichen Bedingungsgleichungen, die ins Spiel kommen, um die speziellen Verbindungen zwischen den Elementen zu berücksichtigen. Die speziellen Verbindungen sind diejenigen, die kein Moment übertragen, Querkraft, oder Axialkraft.

Als Beispiel, Betrachten Sie die Struktur im Bild unten (oberer Abschnitt), es wird eindeutig durch drei Reaktionen gestützt, aber diese reichen nicht aus, um das Gleichgewicht unter den aufgebrachten Kräften in der Ebene zu garantieren, dank des Vorhandenseins des Scharniers zwischen den Elementen, es braucht eine vierte nicht parallele, nicht gleichzeitige Reaktion, um ein Gleichgewicht zu gewährleisten (unterer Abschnitt).

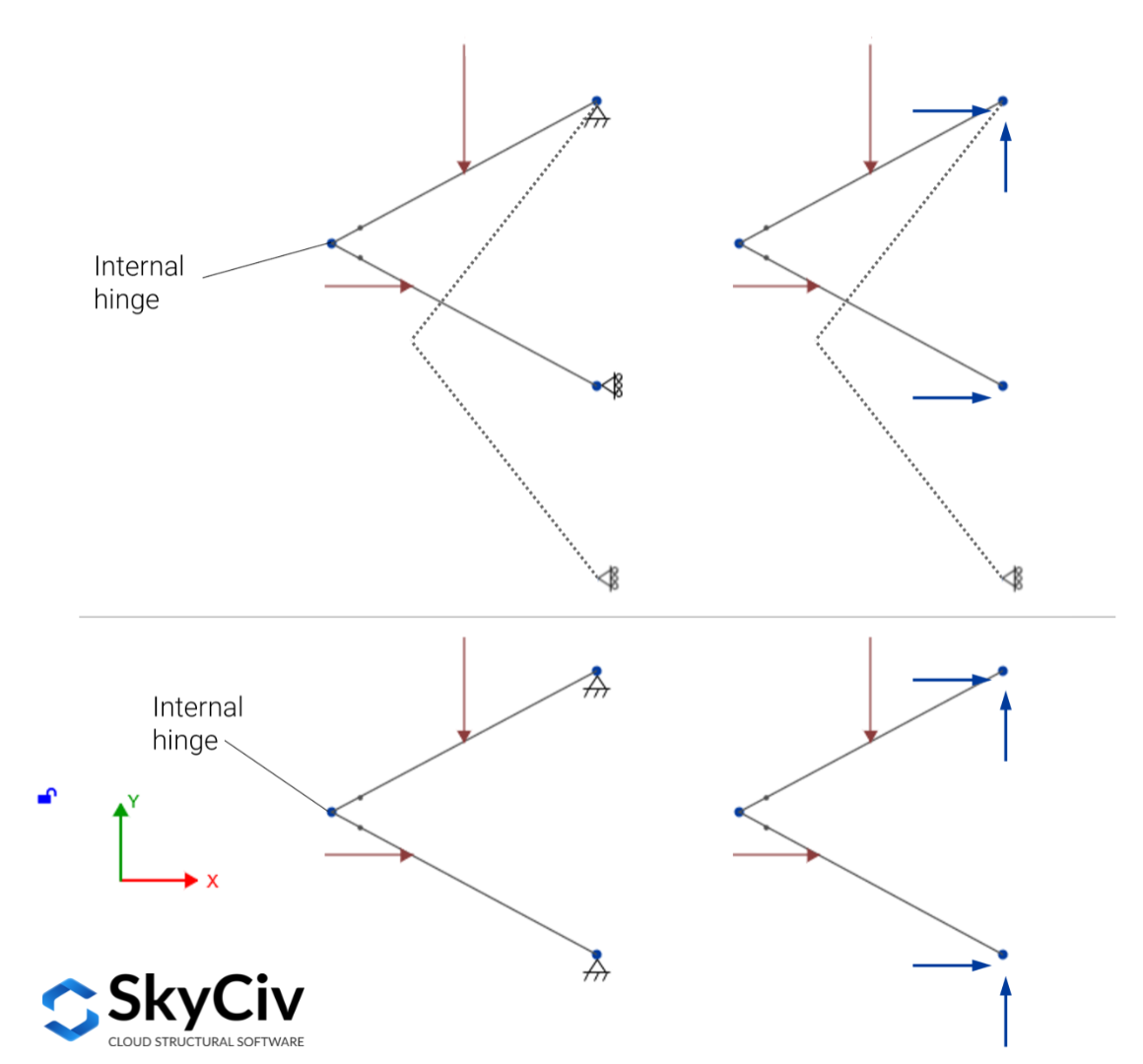
Im Allgemeinen, für innerlich instabile Strukturen, basierend auf der Anzahl der Reaktionen \(R) und Zustandsgleichungen \(e_c\), es ist möglich, die statische Bestimmtheit zu bestimmen, Unbestimmtheit, und Instabilität von intern stabilen Strukturen unter Verwendung der folgenden Kriterien:

\( r begin{Fälle} < 3 + e_c, \; \textrm{statisch instabile äußere Struktur} \\ = 3 + e_c, \; \textrm{statisch bestimmte äußere Struktur} \\ > 3 + e_c, \; \textrm{statisch unbestimmte äußere Struktur} \Ende{Fälle}\)

Für unbestimmte äußerlich innerlich instabile Strukturen, Der Grad der externen Unbestimmtheit kann wie folgt ausgedrückt werden:

\(i_e = r – (3 + e_c)\)

Einpacken

Für flächige Strukturen, die intern stabil sind, um extern stabil zu sein, was bedeutet, dass es unter einem allgemeinen Lastsystem im Gleichgewicht bleibt, Folgendes muss gelten:

• Die Struktur wird durch drei oder mehr Reaktionen unterstützt
• Alle Reaktionen können nicht parallel oder gleichzeitig ablaufen

Für planare Strukturen, die intern instabil sind, um extern stabil zu sein, was bedeutet, dass es unter einem allgemeinen Lastsystem im Gleichgewicht bleibt, Folgendes muss gelten:

• Die Anzahl der die Struktur stützenden Reaktionen ist größer oder gleich der Anzahl der Bedingungsgleichungen plus drei
• Alle Reaktionen können nicht parallel oder gleichzeitig ablaufen

Fehlerbehebung bei einer instabilen Struktur in S3D

Es gibt ein paar Dinge, die Sie ausprobieren können, wenn das Modell nicht aufgelöst wird, und du bekommst die “Instabile Struktur” Fehlermeldung:

• Wählen Sie alle Stäbe aus und vergewissern Sie sich, dass sie ihre Stäbe am Ende haben “FFFFFF”, und versuchen Sie, das Modell auszuführen. Wenn einige Mitglieder im endgültigen Modell eine andere Endbefestigung haben müssen, Beginnen Sie, es nacheinander zu ändern, und lösen Sie die Struktur, um zu sehen, welches das genaue Mitglied oder der Satz von Mitgliedern ist, das die Instabilität verursacht.
• Wählen Sie alle Stäbe aus und ändern Sie ihren Typ von normal zu kontinuierlich, Dadurch würden Stäbe richtig verbunden, die keinen Knoten im Schnittpunkt haben, aber verbunden werden sollen.
• Unterdrücken Sie alle Kabel aus der Analyse, und versuchen, das Modell zu lösen. Zu lernen, wie man Mitglieder unterdrückt, beziehen auf Dieser Artikel.

Verweise

Kassimali, Islam. „3.4 Statische Bestimmtheit, Unbestimmtheit, und Instabilität.“ Strukturanalyse, Cengage-Lernen, 2011.