Ein vollständig ausgearbeitetes Beispiel der Windlastberechnung für Schilder mit EN 1991-1-4
In diesem Artikel, Wir werden diskutieren, wie die Windlasten auf Schildern mit EN berechnet werden 1991-1-4 befindet sich in Oxfordshire, Großbritannien. Unsere Referenzen werden die EN sein 1991-1-4 Aktion auf Strukturen (Windlast) und BS EN 1991-1-4 Nationaler Anhang. Wir werden ähnliche Daten in verwenden IM 1991-1-4 Beispiel für die Berechnung der Windlast.
SkyCiv automatisiert die Windgeschwindigkeitsberechnungen mit ein paar Parametern. Probier unser Schilder-Windlast-Rechner:
Strukturdaten
In diesem Beispiel, Wir verwenden die folgenden Daten. Wir werden nur überlegen Windquellenrichtung gleich 240°. Außerdem, das Die Bodenhöhe des Geländes beträgt 57,35 m.
Tabelle 1. Die Schilderdaten, die für unsere Windlastberechnung benötigt werden.
| Ort | Oxfordshire, Vereinigtes Königreich |
| Belegung | Verschiedenes – Schild |
| Terrain | Flaches Ackerland |
| Unterschreiben Sie die horizontale Dimension, b | 12.0 m |
| Zeichen horizontal vertikal, h |
12.0 m |
| Boden bis Oberkante Schild, H. |
50.0m |
| Masse-zu-Schild-Schwerpunkt, mite |
44.0 m |
| Bezugsfläche des Schildes AZeichen |
144.0 qm. |
| Stangendurchmesser, d |
1.0 m |
| Art der Poloberfläche |
Gusseisen |
| Boden bis zur Spitze des Pols, mitG |
38.0 m |
| Bezugsfläche von Pol APole |
38.0 m |
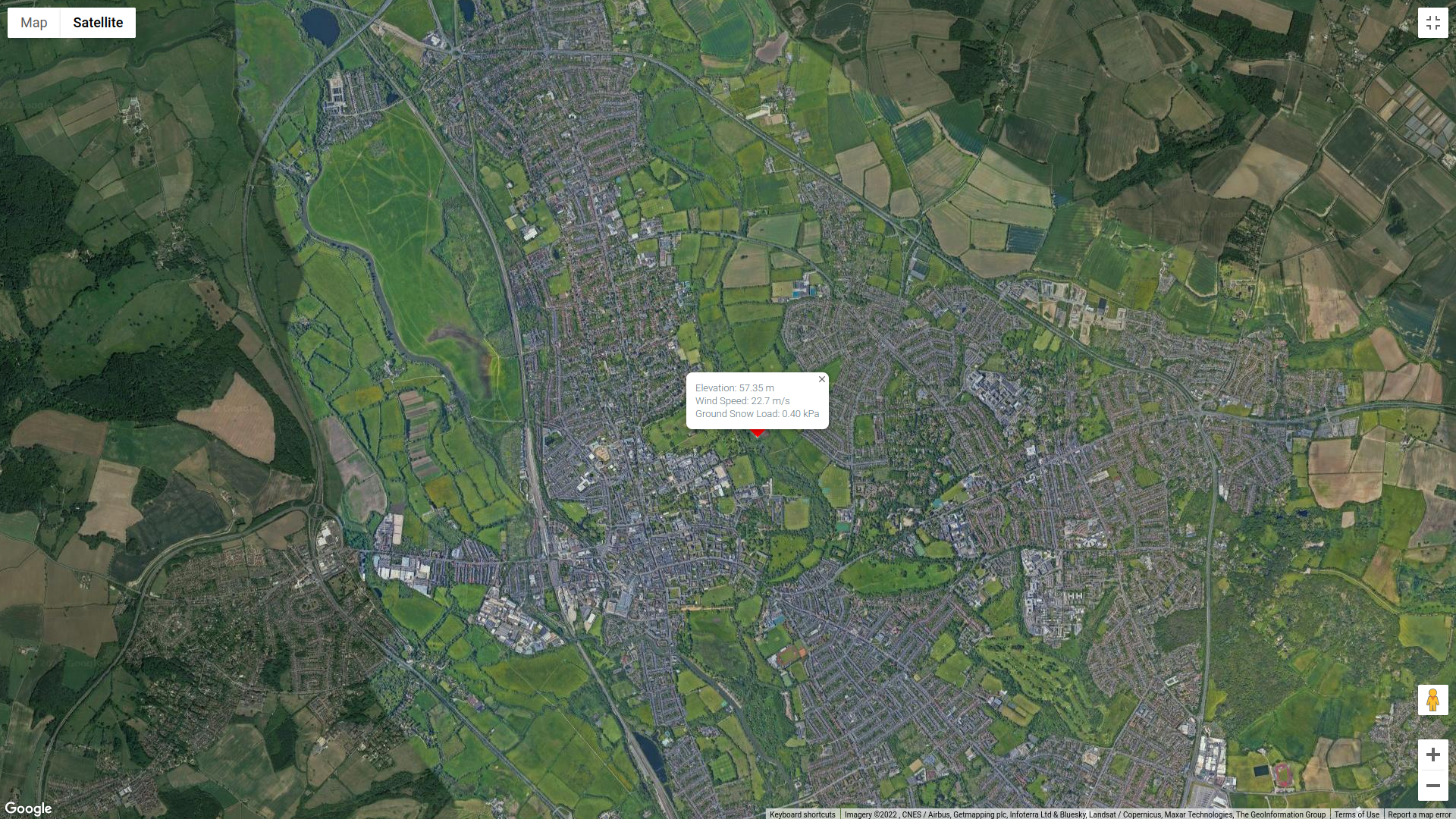
Zahl 1. Standort (von Google Maps).
Zahl 2. Abmessungen des Schildes.
Die Formel zur Bestimmung des Auslegungswinddrucks lautet:
Für die Grundwindgeschwindigkeit:
\({v}_{b} = {c}_{dir} {c}_{Jahreszeit} {c}_{alt} {v}_{b,Karte}\) (1)
Wo:
\({v}_{b}\) = Grundwindgeschwindigkeit in m / s
\({c}_{dir}\) = Richtungsfaktor
\({c}_{Jahreszeit}\)= saisonaler Faktor
\({c}_{alt}\)= Höhenfaktor wo:
\({c}_{alt} = 1 + 0.001A \) zum \( z ≤ 10 \) (2)
\({c}_{alt} = 1 + 0.001A ({10/mit}^{0.2}) \) zum \( mit > 10 \) (3)
\({v}_{b,Karte}\) = Fundamentalwert der Grundwindgeschwindigkeit nach Abbildung NA.1 von BS EN 1991-1-4 Nationaler Anhang
\( A \) = Höhe des Standorts in Metern über dem Meeresspiegel
Für Grundgeschwindigkeitsdruck:
\({q}_{b} = 0.5 {⍴}_{Luft} {{v}_{b}}^{2} \) (4)
Wo:
\({q}_{b}\) = Auslegungswinddruck in Pa
\({⍴}_{Luft}\) = Luftdichte (1.226kg / cu.m.)
\({v}_{b}\)= Grundwindgeschwindigkeit in m / s
Für Spitzendruck:
\({q}_{p}(mit) = 0.5 {c}_{e}(mit){q}_{b} \) für Baustellen in ländlichem Gelände (5)
\({q}_{p}(mit) = 0.5 {c}_{e}(mit){c}_{e,T.}{q}_{b} \) für Baustellen im Stadtgebiet (6)
Wo:
\({c}_{e}(mit)\) = Belichtungsfaktor
\({c}_{e,T.} \) = Belichtungskorrekturfaktor für Stadtgelände
Zur Berechnung der auf das Schild/den Mast wirkenden Windstärke:
\({F.}_{w} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({mit}_{e}){A}_{Ref} \) (7)
Wo:
\( {c}_{s} {c}_{d} \) = Strukturfaktor
\({c}_{f} \) = Kraftbeiwert der Struktur
\({q}_{p}({mit}_{e}) \) = Spitzengeschwindigkeitsdruck auf Referenzhöhe \({mit}_{e} \)
\({A}_{Ref} = bh) = Bezugsfläche der Struktur
Geländekategorie
Basierend auf BS EN 1991-1-4 Nationaler Anhang, die Geländekategorien in EN 1991-1-14 wurden aggregiert 3 Kategorien: Geländekategorie 0 wird als Meer bezeichnet; Die Geländekategorien I und II wurden als Landgelände betrachtet, und die Geländekategorien III und IV wurden als Stadtgelände betrachtet.
Betrachtet man den Wind aus 240°, Wir können die Geländekategorie des gegen den Wind liegenden Geländes als klassifizieren Städtisches Gelände.
Richtungs- und Jahreszeitfaktoren, \({c}_{dir}\) & \({c}_{Jahreszeit}\)
Um für Gleichung zu berechnen (1), Wir müssen die Richtungs- und Jahreszeitfaktoren bestimmen, \({c}_{dir}\) & \({c}_{Jahreszeit}\). Aus Tabelle NA.1 von BS EN 1991-1-4 Nationaler Anhang, da die Windquellenrichtung 240° beträgt, den entsprechenden Wert für den Richtungsfaktor, \({c}_{dir}\), entspricht 1.0.
Andererseits, wir wollen einen konservativen Fall für den Jahreszeitenfaktor betrachten, \({c}_{Jahreszeit}\), was wir werden einstellen 1.0.
Höhenfaktor \({c}_{alt}\)
Zum Höhenfaktor, \({c}_{alt}\), Wir werden nur Gleichung verwenden (2) für einen konservativeren Ansatz mit Standorterhöhung \( A \) gleich 57,35 m. Deshalb:
\({c}_{alt} = 1 + 0.001(57.35) = 1.05735\)
Grundlegende Windgeschwindigkeit und Druck, \({v}_{b}\) & \({q}_{b}\)
Die Windgeschwindigkeitskarte für das Vereinigte Königreich kann der Abbildung NA.1 des Nationalen Anhangs für BS EN entnommen werden 1991-1-4.
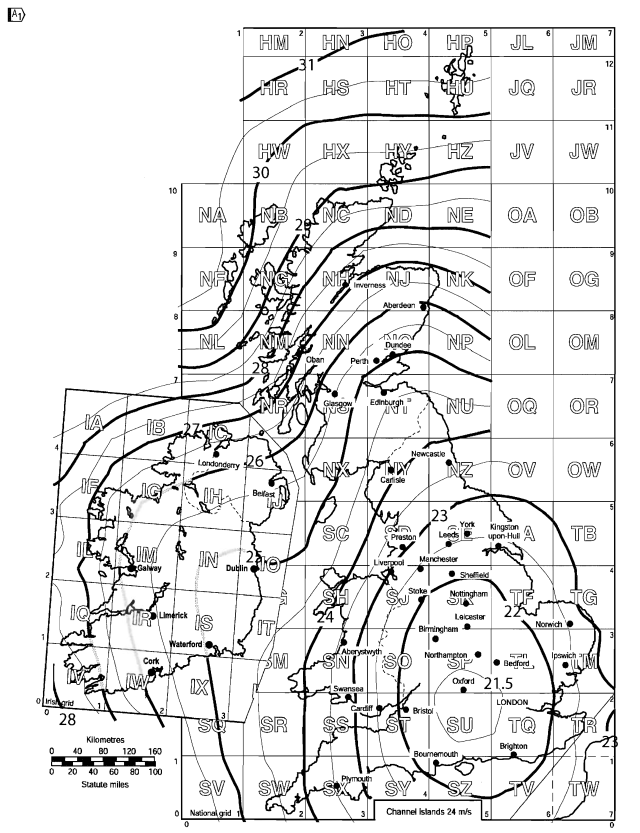
Zahl 5. Grundlegende Windgeschwindigkeit für das Vereinigte Königreich basierend auf Abbildung NA.1 von BS EN 1991-1-4 Nationaler Anhang.
Für unseren Standort, Oxfordshire, England, das berechnete \( {v}_{b,Karte} \) entspricht 22.7 Frau.
\( {v}_{b} = {c}_{dir} {c}_{Jahreszeit} {c}_{alt} {v}_{b,Karte} = (1.0)(1.0)(1.05735)(22.7) \)
\( {v}_{b} = 24.0 Frau \)
Wir können den grundlegenden Winddruck berechnen, \( {q}_{b,0} \), unter Verwendung von Gleichungen (4):
\( {q}_{b} = 0.5(1.226)({24}^{2}) = 353.09 Gut \)
SkyCiv automatisiert jetzt die Erkennung von Windregionen und das Abrufen des entsprechenden Windgeschwindigkeitswerts mit nur wenigen Eingaben. Probier unser SkyCiv Free Wind Tool
Orographiefaktor \({c}_{Das}(mit)\)
Für diese Struktur, das Gelände ist relativ flach für den Wind aus 240°, das
Höhenfaktor, \({c}_{alt}\), Wir werden nur Gleichung verwenden (2) für einen konservativeren Ansatz mit Standorterhöhung \( A \) gleich 57,35 m. Deshalb:
Spitzengeschwindigkeitsdruck, \({q}_{p}(mit)\)
Für unsere Struktur, da die Geländekategorie als Stadtgelände klassifiziert ist, der Höhepunkt ähnlich, der Spitzengeschwindigkeitsdruck, \({q}_{p}(mit)\), kann mit Gleichung gelöst werden (6):
\({q}_{p}(mit) = {c}_{e}(mit){c}_{e,T.}{q}_{b} \)
Wo:
\({c}_{e}(mit)\) = Expositionsfaktor basierend auf Abbildung NA.7 von BS EN 1991-1-4 Nationaler Anhang
\({c}_{e,T.} \) = Belichtungskorrekturfaktor für Stadtgelände basierend auf Abbildung NA.8 von BS EN 1991-1-4 Nationaler Anhang
Zur Bestimmung des Belichtungsfaktors, \({c}_{e}(mit)\) , für das Schild, wir müssen die berechnen \(mit – {h}_{dis}\) und die Entfernung gegen den Wind zur Küste in km. Der Einfachheit halber, Wir werden die Verschiebungshöhe einstellen, \({h}_{dis}\), zu 0. Für die \(mit \) Werte, wir werden es in Erwägung ziehen \(z = 38.0\) und \(z = 44.0\). Außerdem, Die Entfernung gegen den Wind zur Küste beträgt mehr als 100 km. Deshalb, unter Verwendung von Abbildung NA.7 von BS EN 1991-1-4 Nationaler Anhang:
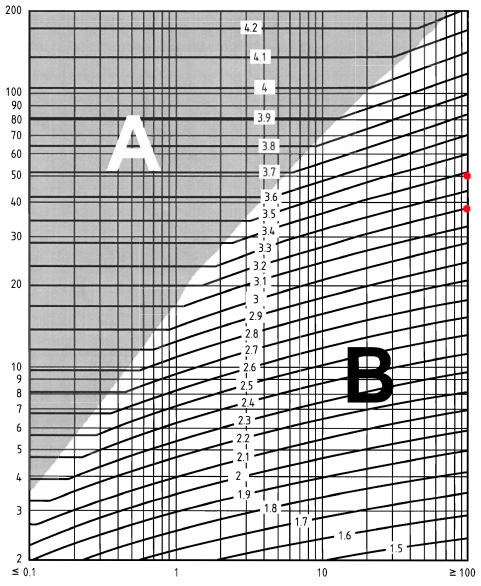
Zahl 6. Abbildung NA.7 von BS EN 1991-1-4 Nationaler Anhang.
Deshalb:
\({c}_{e}(38.0) = 3.2\)
\({c}_{e}(44.0) = 3.3\)
Andererseits, der Belichtungskorrekturfaktor \( {c}_{e,T.} \) für das Schild können aus Abbildung NA.8 der BS EN bestimmt werden 1991-1-4 Nationaler Anhang. Verwenden Sie eine Entfernung innerhalb des Stadtgeländes von 1 km, wir können den Belichtungskorrekturfaktor erhalten \( {c}_{e,T.} \):
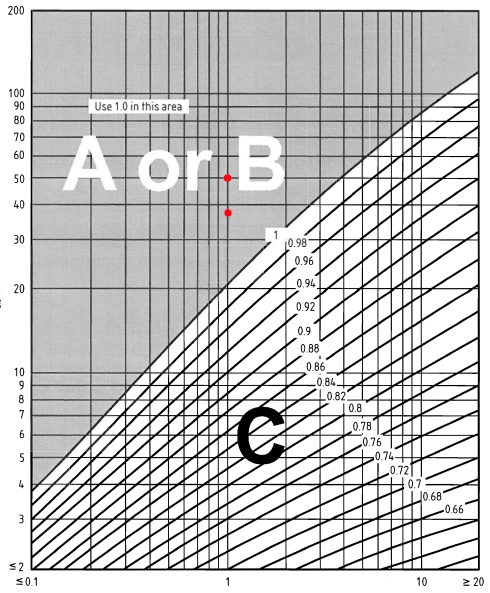
Zahl 7. Abbildung NA.8 von BS EN 1991-1-4 Nationaler Anhang.
Deshalb:
\({c}_{e,T.}(38.0) = 1.0\)
\({c}_{e,T.}(44.0) = 1.0\)
Verwenden Sie die obigen Werte, Wir können den Spitzengeschwindigkeitsdruck berechnen, \({q}_{p}(mit)\), zum \(z = 38.0\) und \(z = 50.0\):
\({q}_{p}(44.0) = (3.3)(1.0)(353.09) = 1165.20 Gut \)
\({q}_{p}(38.0) = (3.2)(1.0)(353.09) = 1129.89 Gut \)
Struktureller Faktor, \( {c}_{s}{c}_{d} \)
Für unser Schild, Wir verwenden einen vereinfachten Wert für den Strukturfaktor, \({c}_{s}{c}_{d}\), gleich sein 1.0 basierend auf Abschnitt 6 oder und 1991-1-4.
Kraftkoeffizient, \( {c}_{f}\), für Schild
Für Schilder, der Kraftbeiwert, \({c}_{f}\), entspricht 1.8 basierend auf Abschnitt 7.4.3 oder und 1991-1-4.
Windkraft, \( {F.}_{w,Schild} \), Handeln auf dem Schild
Die auf das Schild wirkende Kraft kann mit Gleichung berechnet werden (7) basierend auf Abschnitt 5.3(2) oder und 1991-1-4.
\({F.}_{w,Schild} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({mit}_{e}){A}_{Ref,Schild} = (1.0)(1.8)(1165.20Gut)(12.0m)(12.0m)\)
\({F.}_{w,Schild} = 302019.84 N)
Beachten Sie, dass die horizontale Exzentrizität dieser Windkraft, die auf den Schwerpunkt des Schildes wirkt, 3,0 m betragen sollte.
Die Windberechnungen können alle mit dem SkyCiv Load Generator für EN durchgeführt werden 1991 (Windlastrechner für Schilder und Masten). Benutzer können den Standort eingeben, um die Windgeschwindigkeit und Geländedaten zu erhalten, Geben Sie die Solarmodulparameter ein und generieren Sie die Auslegungswinddrücke. Mit der Standalone-Version, Sie können diesen Prozess rationalisieren und erhalten einen detaillierten Windlastberechnungsbericht für Schilder und Masten!
Windkraft, \( {F.}_{w,Pole} \), an der Stange wirken
Ähnlich, Die auf den Pol wirkende Kraft kann mit Gleichung berechnet werden (7) basierend auf Abschnitt 5.3(2) oder und 1991-1-4.
\({F.}_{w,Pole} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({mit}_{G}){A}_{Ref,Pole}\) (8)
Wo:
\({c}_{f} = {c}_{f,0}{ψ}_{λ} \)
\({A}_{Ref,Pole} = {mit}_{G}d \)
Hinweis:
\(ψ_{λ} \) wird anhand der effektiven Schlankheit berechnet, \( λ \), Verwendung von Abbildung 7.36 der Sektion 7.13 oder und 1991-1-4
\({c}_{f,0}\) wird basierend auf der Reynolds-Zahl berechnet \( R_{e} \) mit Abbildung 7.28 oder und 1991-1-4
Wo:
\( {mit}_{G} \) ist die Höhe des Mastes vom Boden in m
\( d \) ist der Durchmesser des Mastes in m
\( n = 0.000015 qm/s \) ist die kinematische Viskosität der Luft
\( v({mit}_{G}) = (2{q}_{p}({mit}_{G})/r)^{0.5} \) (9)
\( {R.}_{e} = V(z_{G})d/ n \) (10)
Wir werden in den nächsten Abschnitten tief in diese Parameter eintauchen
Reynolds Nummer, \( {R.}_{e} \), für die Stange
Verwenden Sie die oben berechneten Werte, wir können rechnen \( v({mit}_{G}) \) unter Verwendung von Gleichung (9):
\( v({mit}_{G}) = (2{q}_{p}({mit}_{G})/r)^{0.5} = (2(1129.89)/(1.226))^{0.5} \)
\( v({mit}_{G}) = 42.93 Frau)
Deshalb, die Reynolds-Zahl \( R_{e} \) für die Stange, unter Verwendung von Gleichung (10) ist:
\( {R.}_{e} = V({mit}_{G})d/ v = (42.93)(1.0)/(0.000015) \)
\( {R.}_{e} = 2862000 \)
Kraftkoeffizient, \( {c}_{f0} \), ohne freien Endfluss
Das Stangenmaterial, das wir verwendet haben, ist Gusseisen, das hat äquivalente Oberflächenrauhigkeit \( k \) gleich 0.2 basierend auf Tabelle 7.13 oder und 1991-1-4.
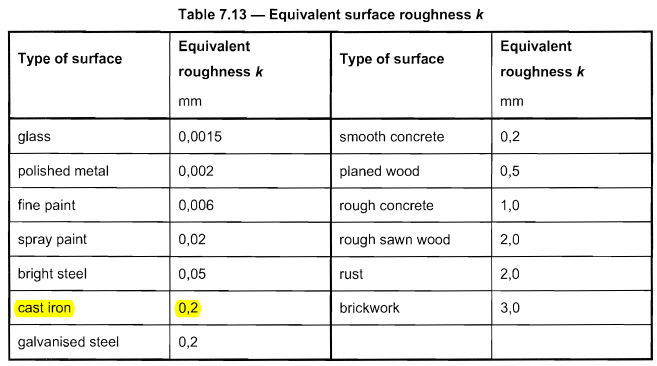
Zahl 8. Tabelle 7.13 oder und 1991-1-4 für äquivalente Rauheit \( k \).
Der Kraftbeiwert \( {c}_{f0} \) kann mit der Formel aus Abbildung bestimmt werden 7.28 von EN 1991-1-4 mit \( k/d = 0.2\):
\( {c}_{f0}= 1.2 + {0.18Protokoll(10 k/d)}/{1 + 0.4Protokoll({R.}_{e}/{10}^{6}} = 1.2 + {0.18Protokoll(10 (0.2)}/{1 + 0.4Protokoll((2862000)/{10}^{6}}\)
\( {c}_{f0} = 1.246 \)
Effektive Schlankheit, \( λ \)
Die effektive Schlankheit, \( λ \), für den Pol können aus Tabelle Nr. 4 ermittelt werden 7.16 oder und 1991-1-4.
\( λ = max(0.7 {mit}_{G}/d, 70) \) zum \( {mit}_{G} \) > 50m
\( λ = max({mit}_{G}/d, 70) \) zum \( {mit}_{G} \) < 15m
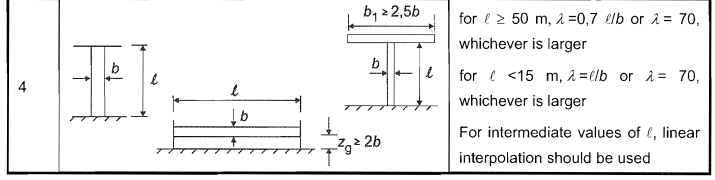
Zahl 9. Tabelle 7.16 oder und 1991-1-4 zur Berechnung der effektiven Schlankheit \( λ \).
Schon seit \( {mit}_{G} \) entspricht 38,0 m, wir müssen die Werte von interpolieren \( λ \) für 50m und 15m:
\( {mit}_{G} = 38\)
\( {λ}_{50m} = max(0.7 (38), 70) = 70 \)
\( {λ}_{15m} = max((38), 70) = 70 \)
Deshalb:
\( λ = 70 \)
Endeffektfaktor, \( {ψ}_{λ} \)
Der Endeffektfaktor, \( {ψ}_{λ} \), kann mit Abbildung abgerufen werden 7.36 oder und 1991-1-4 erfordert das Festigkeitsverhältnis \( Phi \) und effektive Schlankheit \( λ \). Wir gehen von einem Festigkeitsverhältnis aus \( Phi \) gleich 1.0 da die Rohrsäule keine Perforation aufweist.
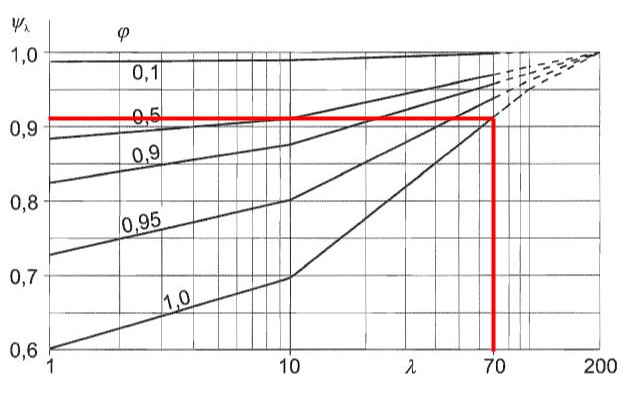
Zahl 10. Der entsprechende Endeffektfaktor \( {ψ}_{λ} \) für den Mast, der das Schild trägt, basierend auf Abbildung 7.36 oder und 1991-1-4.
Aus der Abbildung 10, wir können daraus den Endeffektfaktor ableiten \( {ψ}_{λ} \) denn der Pol ist gleich 0.910.
Aus den oben berechneten Parametern,das können wir schon berechnen Windkraft, \( {F.}_{w,Pole} \):
\({c}_{f} = {c}_{f,0}{ψ}_{λ} = (1.246)(0.910) = 1.134\)
\({F.}_{w,Pole} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({mit}_{e}){A}_{Ref,Pole} = (1.0)(1.134)(1129.89)(38.0×1.0) \)
\({F.}_{w,Pole} = 48689.22 N. \)
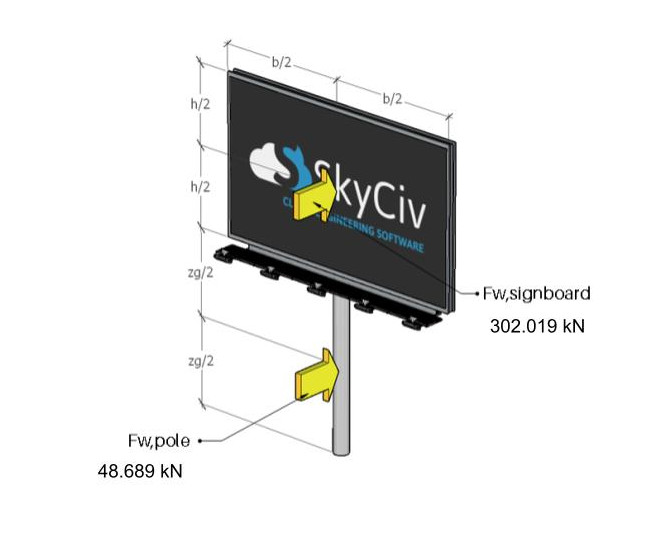
Zahl 11. Die auf Schild und Mast wirkenden Windkräfte.
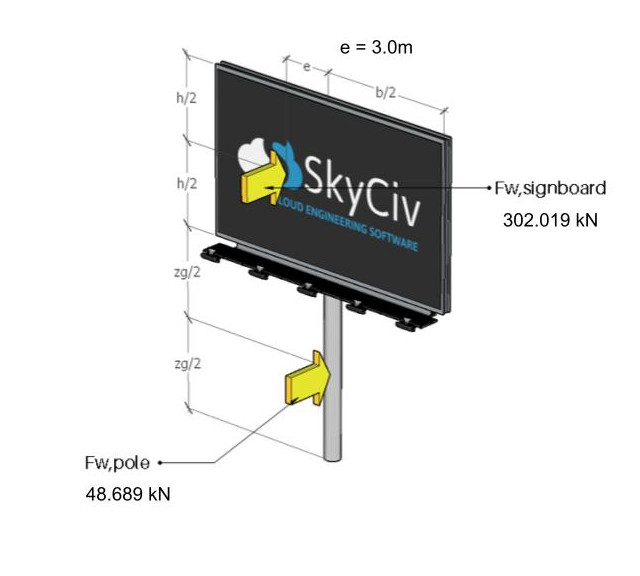
Zahl 12. Die auf Schild und Mast wirkenden Windkräfte sind dabei exzentrisch.
SkyCiv Lastgenerator
Verwenden des SkyCiv-Lastgenerators, Mit nur wenigen Klicks und Eingaben erhalten Sie Windlasten für Schilder und Masten. Wenn Sie die Standalone-Version kaufen oder sich für ein Professional-Konto anmelden, Sie können den detaillierten Windbericht für Ihr Schilderprojekt erstellen!
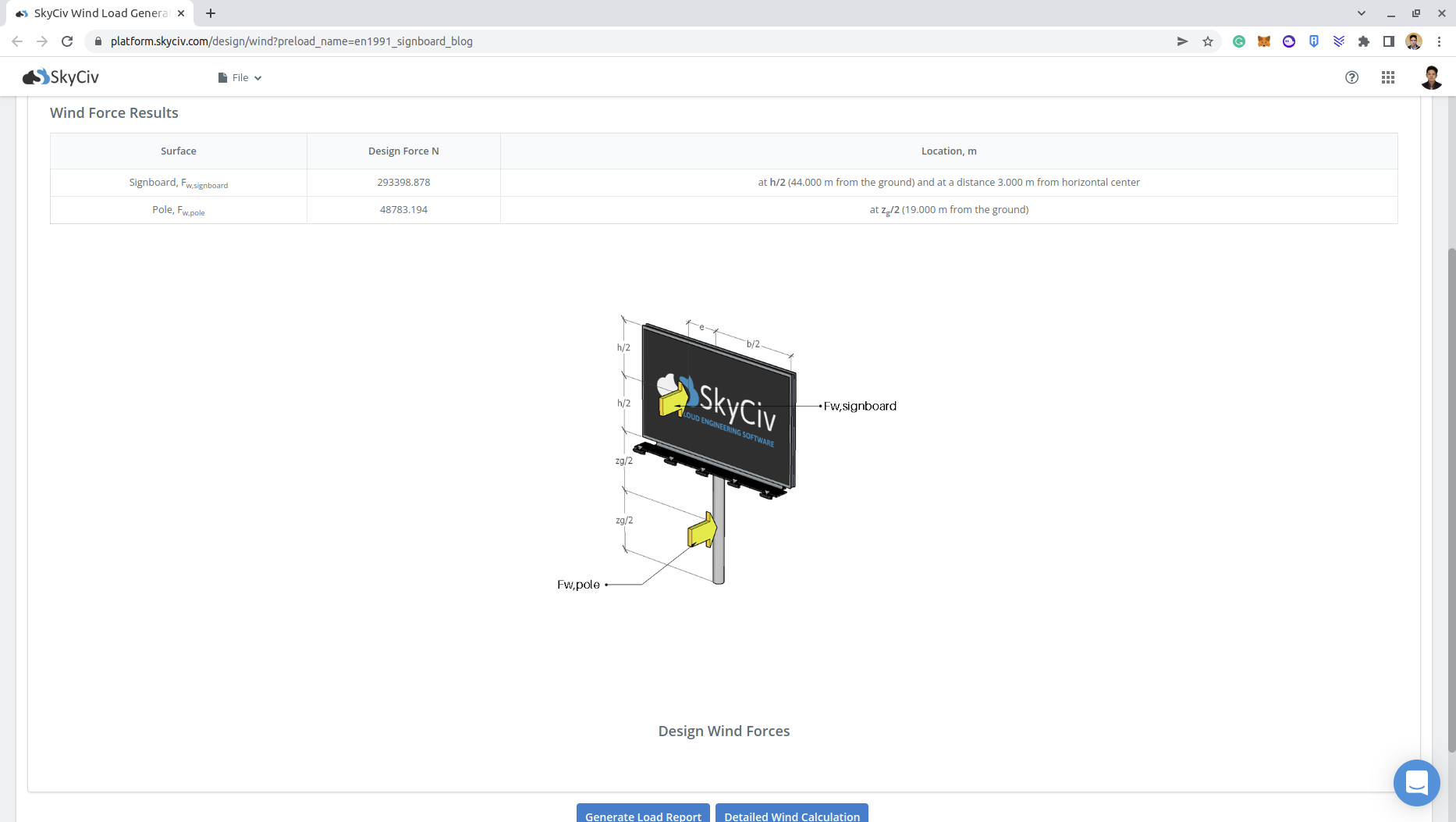
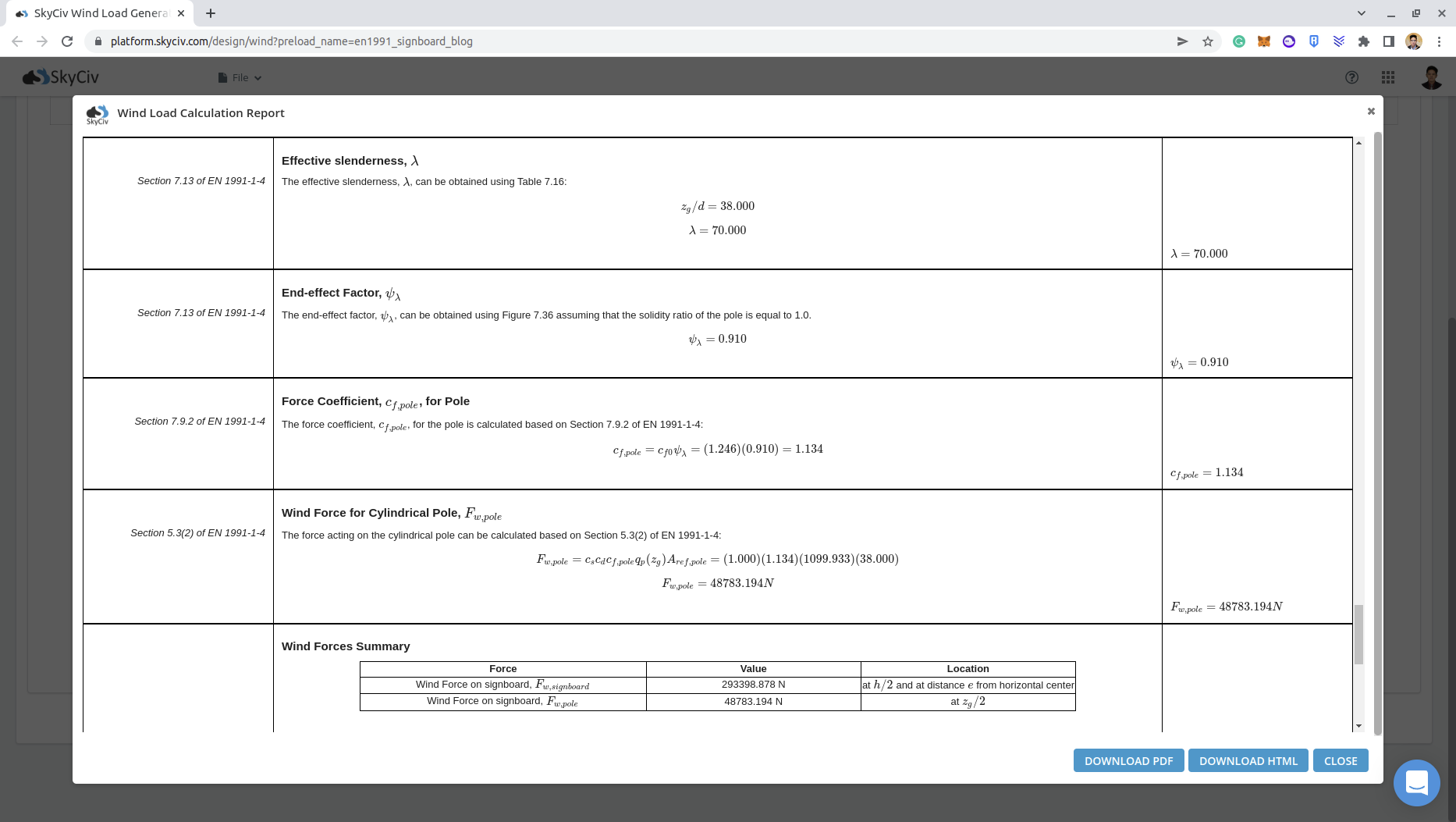
Sie können den detaillierten Windlastbericht für das Schild über diese Links einsehen:
Statiker, Produktentwicklung
MS Bauingenieurwesen
Verweise:
- Im, B.. (2005). Eurocode 1: Aktionen auf Strukturen - Teil 1–4: Allgemeine Aktionen - Windaktionen.
- BSI. (2005). BS EN 1991-1-4: 2005+ A1: 2010: Eurocode 1. Aktionen an Strukturen. Allgemeine Aktionen. Windaktionen.
