Ein voll funktionsfähiges Beispiel für Bodenmontage Berechnung der Windlast und des Schneedrucks von Solarmodulen mit ASCE 7-16
[object Window], Eine der am schnellsten wachsenden Industrien als Lösung für dieses Problem ist die Nutzung von Solarenergie. Außerdem, Eine der am schnellsten wachsenden Industrien als Lösung für dieses Problem ist die Nutzung von Solarenergie. Eine der am schnellsten wachsenden Industrien als Lösung für dieses Problem ist die Nutzung von Solarenergie, Eine der am schnellsten wachsenden Industrien als Lösung für dieses Problem ist die Nutzung von Solarenergie. Die Notwendigkeit, die Windlast auf Sonnenkollektoren sowie den Schneedruck zu berechnen, ist entscheidend für diese, um eine lange Lebensdauer zu erreichen. In diesem Artikel, Wir werden diskutieren, wie die Schnee- und Windlasten auf Freiflächen-Solarmodulen mit ASCE berechnet werden 7-16.
SkyCiv automatisiert die Windgeschwindigkeitsberechnungen mit ein paar Parametern. Probier unser Rechner für die Windlast von Solarmodulen
Strukturdaten
In diesem Beispiel, Wir verwenden die folgenden Daten:
Tabelle 1. Gebäudedaten, die für unsere Wind- und Schneelastberechnung benötigt werden.
| Ort | 395 Rocky Point Rd, Cordova, Memphis, Tennessee |
| Belegung | Verschiedenes – Sonnenkollektor |
| Terrain | Flaches Ackerland |
| Plattenbreite | 16.25 ft |
| Plattenlänge | 13.33 ft |
| Montagehöhe | 8.33 ft |
| Neigungswinkel | 30° |
Abbildung 1. Standort (von Google Maps).
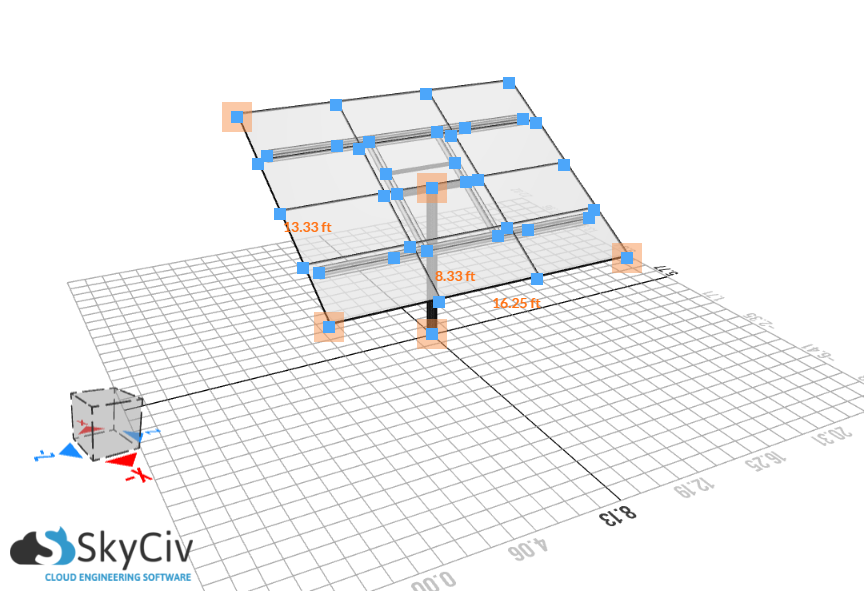
Abbildung 2. Die Abmessungen des Solarmoduls.
Wind laden
Bei der Berechnung der Windlast auf Sonnenkollektoren, Wir werden die ASCE verwenden 7-16 Kapitel 27 – Windlast – Richtverfahren. Wir betrachten das Freiflächen-Solarpanel als offenes Gebäude mit geneigtem Dach, wenn der Neigungswinkel kleiner oder gleich 45° ist und als solides Zeichen für einen Neigungswinkel größer als 45°.
Die Formel zur Bestimmung des Auslegungswinddrucks lautet wie folgt:
Für Neigungswinkel ≤ 45° (gilt als offenes Gebäude mit Schrägdach):
\(p = {q}_{h}G{C}_{N}\) (1)
Für Neigungswinkel > 45° (gilt als solides Zeichen):
\(p = {q}_{h}G{C}_{f}\) (2)
Wo:
\(G\) = Böeneffektfaktor
\({C}_{N}\) = Nettokraftbeiwert für offenes Schrägdach
\({C}_{f}\) = Nettokraftkoeffizient für feste Zeichen
\({q}_{h}\) = Geschwindigkeitsdruck auf Referenzhöhe, \(h\), in psf, gegeben durch die Formel:
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\) (3)
\({K}_{z}\) = Geschwindigkeitsdruckkoeffizient
\({K}_{zt}\)= topographischer Faktor
\({K}_{d}\) = Windrichtungsfaktor
\({K}_{e}\) = Bodenhöhenfaktor
\(V \) = Grundwindgeschwindigkeit in mph
Beachten Sie dies für den Neigungswinkel > 45°, Die zu verwendenden Abmessungen sind die vertikale Projektion des Solarmoduls und verwenden dann die Formel für Nettokraftkoeffizienten für feste Zeichen. Wir werden uns eingehend mit den Details der einzelnen Parameter befassen.
Risikokategorie
Der erste Schritt besteht darin, die Risikokategorie des Solarmoduls basierend auf der Nutzung oder Belegung zu bestimmen. Aus der Tabelle 1.5-1 von ASCE 7-16, können wir das Freiflächen-Solarmodul in diesem Beispiel in die Risikoklasse I einstufen.
Grundlegende Windgeschwindigkeit, \(V\)
Die ASCE 7-16 stellt eine Windkarte bereit, auf der die entsprechende Grundwindgeschwindigkeit eines Standorts aus den Abbildungen 26.5-1A bis 1C ermittelt werden kann. Aus Abbildung 26.5-1A, Cordova, Memphis, Tennessee ist irgendwie in der Nähe des roten Punktes auf der Figur 3 unten, und von dort, die Grundwindgeschwindigkeit, \(V\), ist 100 mph. Beachten Sie, dass der grundlegende Windgeschwindigkeitswert aus den nächstgelegenen Windkonturen interpoliert wird.
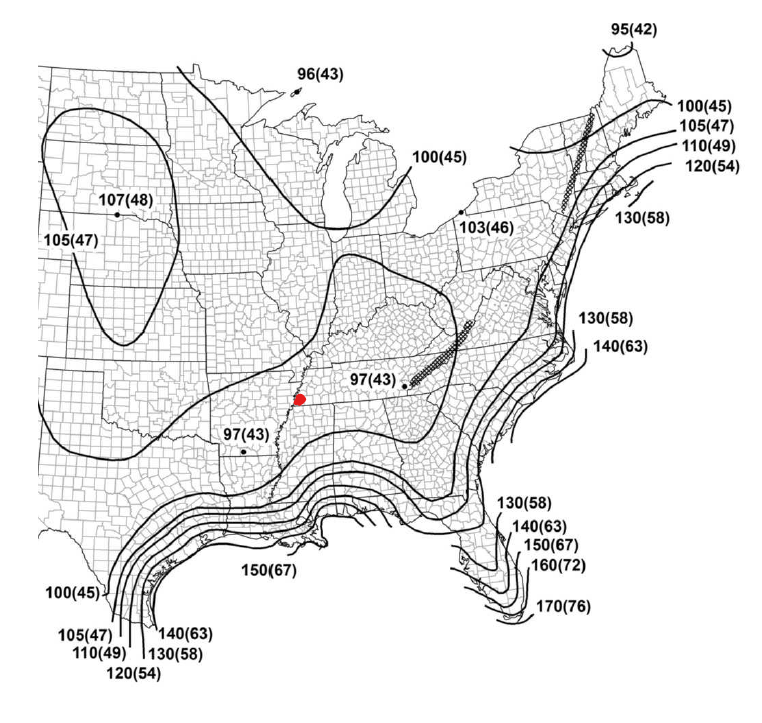
Abbildung 3. Grundlegende Windgeschwindigkeitskarte aus Abbildung 26.5-1A von ASCE 7-16 (Risikoklasse I) mit rotem Punkt, um den Standort unseres Solarpanels anzuzeigen.
SkyCiv automatisiert die Windgeschwindigkeitsberechnungen mit ein paar Parametern. Probier unser Rechner für die Windlast von Solarmodulen
Belichtungskategorie
Abhängig von der analysierten Windrichtung, Die Expositionskategorie des Solarmoduls wird aus dem 45°-Sektor gegen den Wind auf der Grundlage von Abschnitt bestimmt 26.7 von ASCE 7-16. Außerdem, Abschnitt C26.7 enthält Luftaufnahmen, die Beispiele für Expositionen B zeigen, C., und D in den Abbildungen C26.7-5 bis C26.7-7.
In diesem Beispiel, Wir werden nur Wind aus südlicher Richtung verwenden. Daher, anhand der Luftbildbeispiele, Wir können das gegen den Wind liegende Gelände auf der Grundlage von Abbildung C26.7-6 als Exposition C klassifizieren(b) oder “Offenes Gelände mit verstreuten Hindernissen, deren Höhen im Allgemeinen kleiner als sind 30 ft (9.1 Mio.)” wie in Abbildung gezeigt 4 unten. Wir verwenden die Expositionskategorie bei der Berechnung des Geschwindigkeitsdruckkoeffizienten \({K}_{z}\)Spanne> und/oder topografischer Faktor \({K}_{zt}\) wenn benötigt.
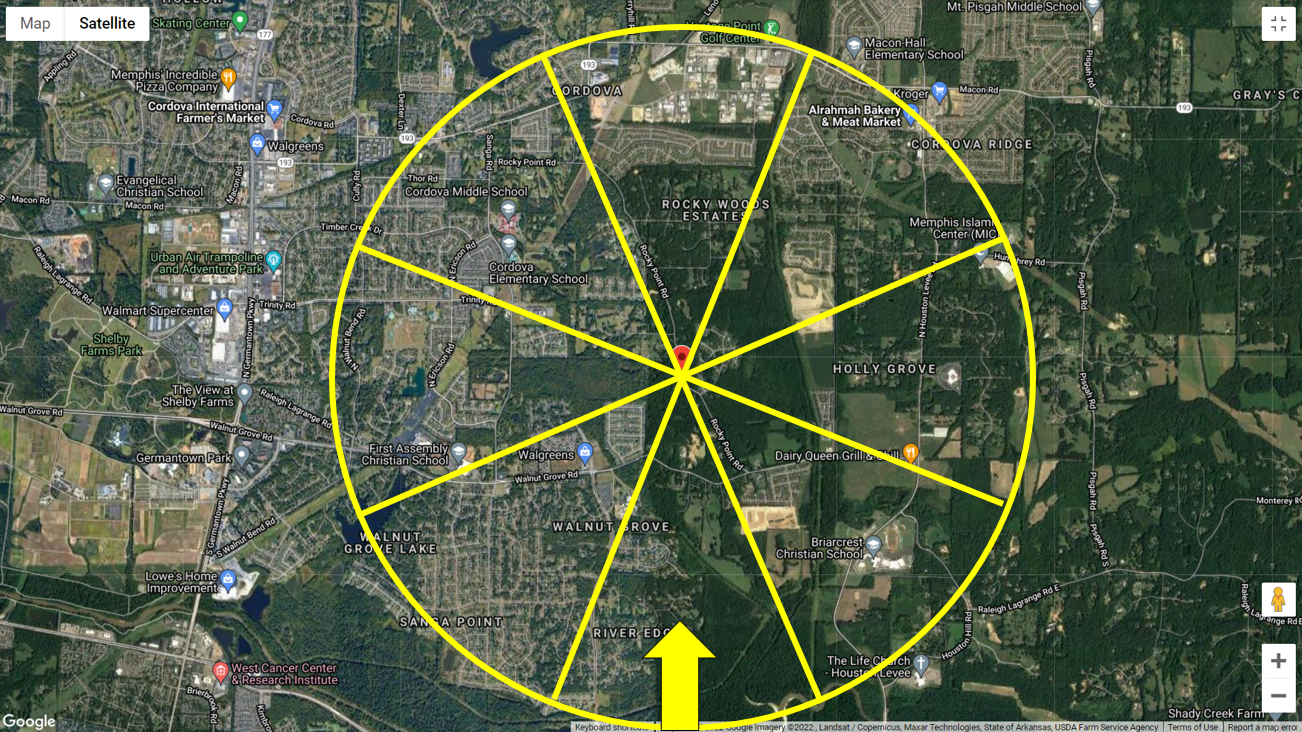
Abbildung 4. Luftbild eines Geländes mit Südwind.
Windrichtungsfaktor, \( {K}_{d} \)
Der Windrichtungsfaktor, \({K}_{d} \), für das Solarpanel ist gleich 0.85 da das Solarpanel als MWFRS betrachtet werden kann (offene Monoslope) wenn der Neigungswinkel kleiner oder gleich 45° ist und als ausgefülltes Zeichen für Neigungswinkel größer als 45° gemäß Tabelle 26.6-1 von ASCE 7-16.
Bodenhöhenfaktor, \( {K}_{e} \)
Der Bodenhöhenfaktor, \({K}_{e} \), kann mit Tabelle berechnet werden 26.9-1 von ASCE 7-16. Für dieses Beispiel, da die Standorthöhe gleich ist 350.48 ft, \({K}_{e} \) kann mit der Formel berechnet werden:
\( {K}_{e} = {e}^{-0.0000362{z}_{g}} \) (4)
\( {K}_{e} = {e}^{-0.0000362(350.48)} = 0.987\)
\( {K}_{e} = 0.987 \)
Gleichung verwenden (4), \({K}_{e} \) entspricht 0.987.
Topographischer Faktor, \( {K}_{zt} \)
Die Parameter zur Berechnung des topografischen Faktors, \({K}_{zt}\), sind in Abbildung detailliert 26.8-1 von ASCE 7-16. Um festzustellen, ob weitere Berechnungen des topografischen Faktors erforderlich sind, wir müssen es mit Abschnitt überprüfen 26.8.1. Wenn der Standort nicht alle aufgeführten Bedingungen erfüllt, dann kann der topografische Faktor als angenommen werden 1.0. Aus der aus Google-Höhen generierten Bodenhöhe, Wir können davon ausgehen, dass das Gelände flach ist, deshalb, \({K}_{zt}\) kann davon ausgegangen werden 1.0 für Wind aus Süd.
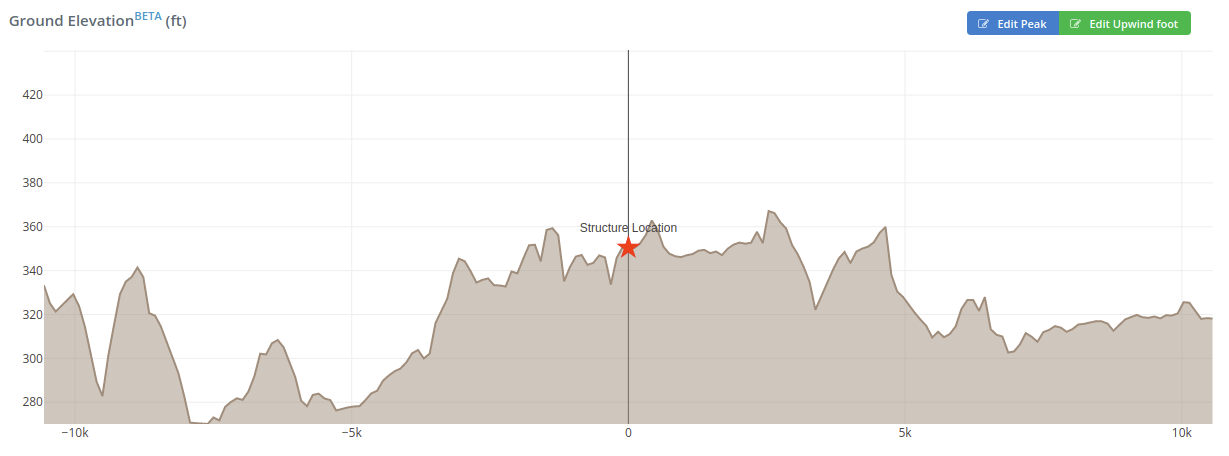
Abbildung 5. Höhenprofil des Standorts in Windrichtung S-N.
Geschwindigkeitsdruckkoeffizient, \({K}_{z}\)
Der Geschwindigkeitsdruckkoeffizient, \({K}_{z}\), kann mit Tabelle berechnet werden 26.10-1 von ASCE 7-16. Dieser Parameter hängt von der Höhe über dem Boden des Punktes ab, an dem der Winddruck berücksichtigt wird, und die Expositionskategorie. Außerdem, Die in der Tabelle angegebenen Werte basieren auf der folgenden Formel:
Für 15ft < \({z}\) < \({z}_{g}\): \({K}_{z} = 2.01(z/{z}_{g})^{2/α}\) (5)
Zum \({mit}\) < 15ft: \({K}_{z} = 2.01(15/{z}_{g})^{2/α}\) (6)
Wo:
Tabelle 3. Werte von α und \({z}_{g}\) vom Tisch 26.11-1 von ASCE 7-16.
| Exposition | ein | \({z}_{g}\) (ft) |
|---|---|---|
| B. | 7 | 1200 |
| C. | 9.5 | 900 |
| D. | 11.5 | 700 |
Für dieses Beispiel, Wir werden die Höhe der Solarmontage berücksichtigen.
\({K}_{z} = 2.01((15)/(900))^{2/(9.5)} = 0.85 \)
\({K}_{z} = 0.85 \)
Geschwindigkeitsdruck
Aus der Gleichung (3), wir können nach dem Geschwindigkeitsdruck lösen, \( {q}_{h}\) in psf, bei Montagehöhe gleich 8.33 ft.
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\)
\({q}_{h} = 0.00256(0.85)(1.0)(0.85)(0.987)(100)^2 = 18.256 psf\)
\({q}_{h} = 18.256 psf\)
Zur Berechnung des Auslegungswinddrucks, Wir werden Gleichung verwenden (1). Details dieser Parameter sind unten gezeigt.
Böeneffektfaktor, \(G\)
Bei der Ermittlung des Böenfaktors, \(G\), Wir müssen zuerst die grundlegende Eigenfrequenz der Struktur berechnen \( {n}_{1} \). Wenn \( {n}_{1} \) ist weniger als 1 Hz, es wird als flexible Struktur klassifiziert, daher müssen wir für berechnen \(G\) Abschnitt verwenden 26.11.5. In diesem Beispiel, für vereinfachte Vorgehensweise, Wir gehen davon aus, dass unser Solarpanel starr ist, wo \(G\) entspricht 0.85 basierend auf Abschnitt 26.11.1 von ASCE 7-16. Es ist zu beachten, dass bei der Bestimmung des Böeneinflussfaktors insbesondere bei flexiblen Strukturen eine sorgfältige Überprüfung der Grundeigenfrequenz der Struktur erforderlich ist, da dieser Parameter dadurch vergrößert wird.
Nettodruckkoeffizient, \({C}_{N}\), Neigungswinkel ≤ 45°
Zur Ermittlung der Nettodruckbeiwerte, \( {C}_{N} \), Wir nehmen das Solarpanel als offenes Gebäude mit geneigtem Dach an. Wir können diese Werte aus Abbildung erhalten 27.3-4 von ASCE 7-16 mit der Annahme von “Klarer Windfluss.” Beachten Sie, dass diese Werte nur für Solarmodule mit einem Neigungswinkel kleiner oder gleich 45° gelten
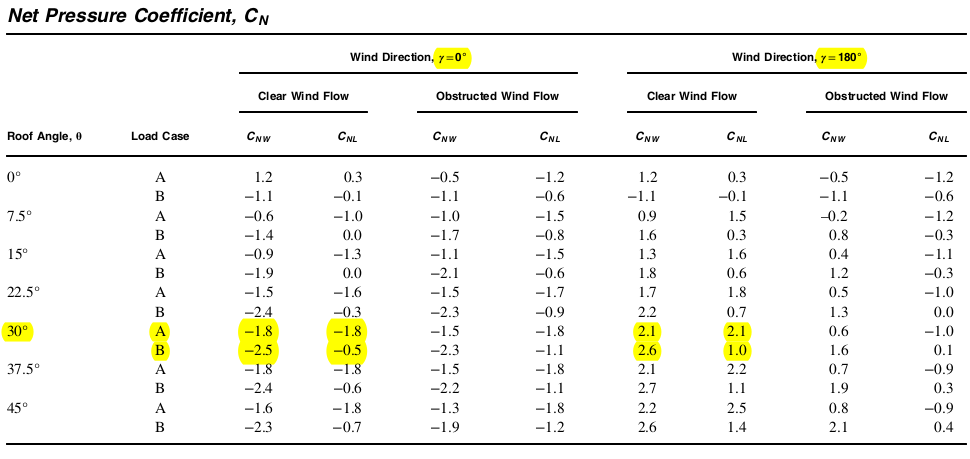
Abbildung 6. Nettodruckkoeffizient, \( {C}_{N} \), Werte aus Abbildung 27.3-4 von ASCE 7-16 für offene Gebäude mit Schrägdach.
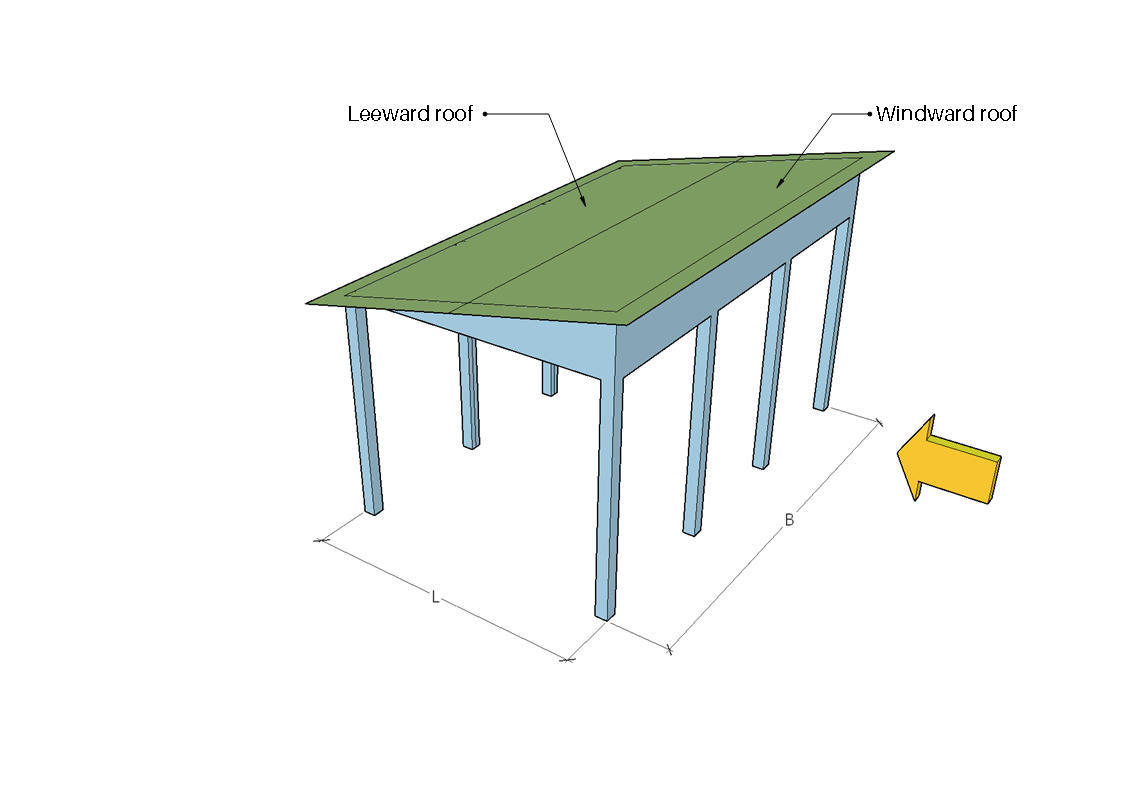
Abbildung 7. Luv- und Leezonen für Richtungswinkel gleich 0° .
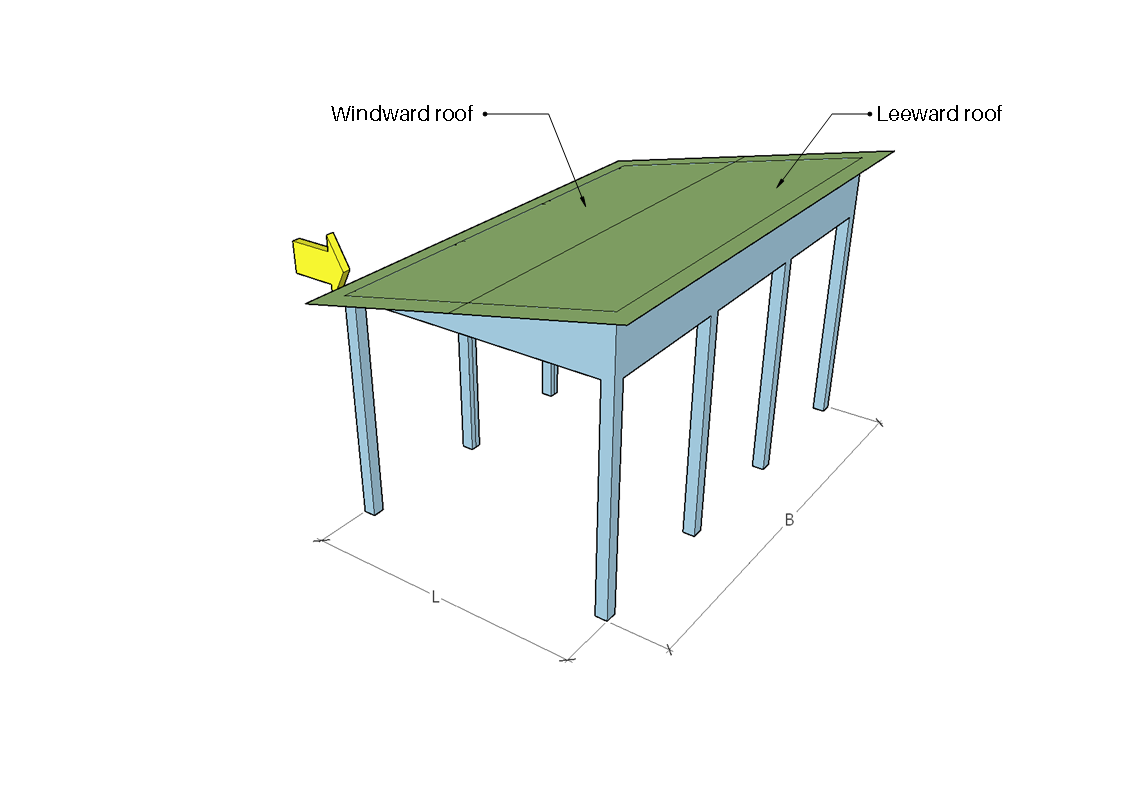
Abbildung 8. Luv- und Leezonen für einen Richtungswinkel von 180°.
Da der Neigungswinkel des Solarpanels gleich 30° ist, die entsprechenden Nettodruckbeiwerte, \( {C}_{N} \), zu verwenden sind wie folgt:
Tabelle 4. Werte von \( {C}_{N} \) zu verwenden basierend auf Abbildung 27.3-4 von ASCE 7-16.
| Lastfall | Richtung = 0° | Richtung = 180° | ||
|---|---|---|---|---|
| \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | |
| Ein | -1.8 | -1.8 | 2.1 | 2.1 |
| B. | -2.5 | -0.5 | 2.6 | 1.0 |
Beachten Sie, dass ein negativer Wert bedeutet, dass der Winddruck von der Oberfläche weg wirkt, und ein positiver Wert bedeutet, dass der Winddruck auf die Oberfläche wirkt. Aus der Tabelle 4, es kann gefolgert werden, dass wir vier betrachten werden (4) Lastfälle für Windlast auf unserem Solarpanel.
Design-Winddruck – Neigungswinkel ≤ 45°
Bei der Berechnung der Windlast auf Sonnenkollektoren mit Neigungswinkel > 45°, Wir werden Gleichung verwenden (1), daher, die Windlasten auf Freiflächen-Solarpanels:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
Tabelle 5. Die berechneten Windlasten von Freiflächen-Solarmodulen sind auf das Bauwerk aufzubringen.
| Lastfall | Richtung = 0° | Richtung = 180° | ||
|---|---|---|---|---|
| Luv, psf |
Lee, psf | Luv, psf | Lee, psf | |
| Ein | -27.932 | -27.932 | 32.587 | 32.587 |
| B. | -38.794 | -7.759 | 40.346 | 15.518 |
Deshalb, Die Windlasten auf bodenmontierte Solarmodule bei Anwendung sind wie folgt:
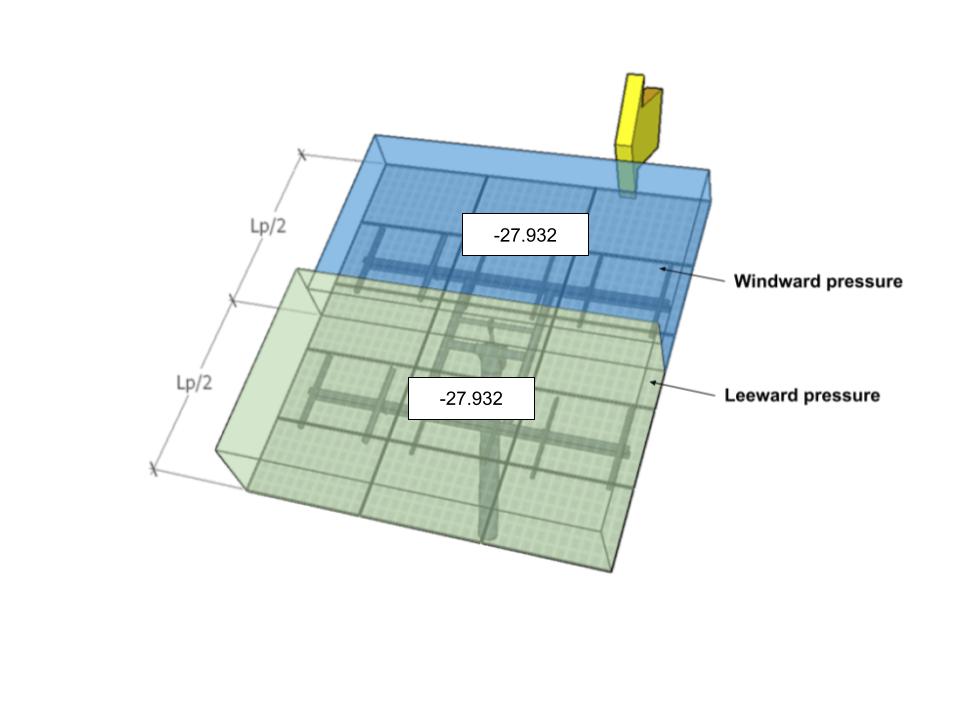
Abbildung 9. Auslegungswinddruck für Richtungswinkel 0° – Lastfall A.
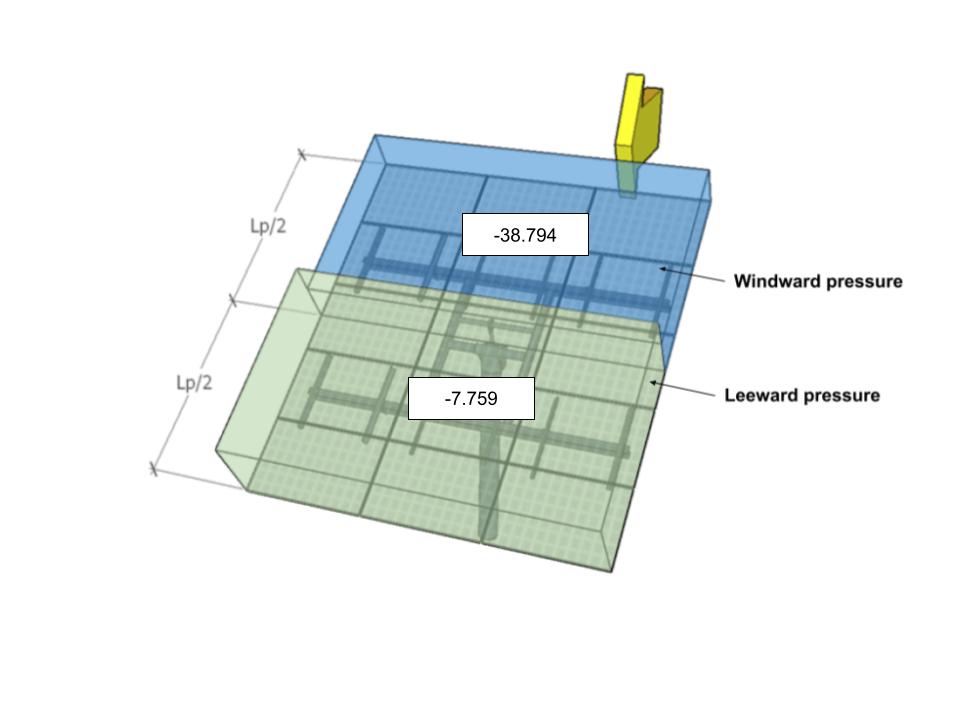
Abbildung 10. Auslegungswinddruck für Richtungswinkel 0° – Lastfall B.
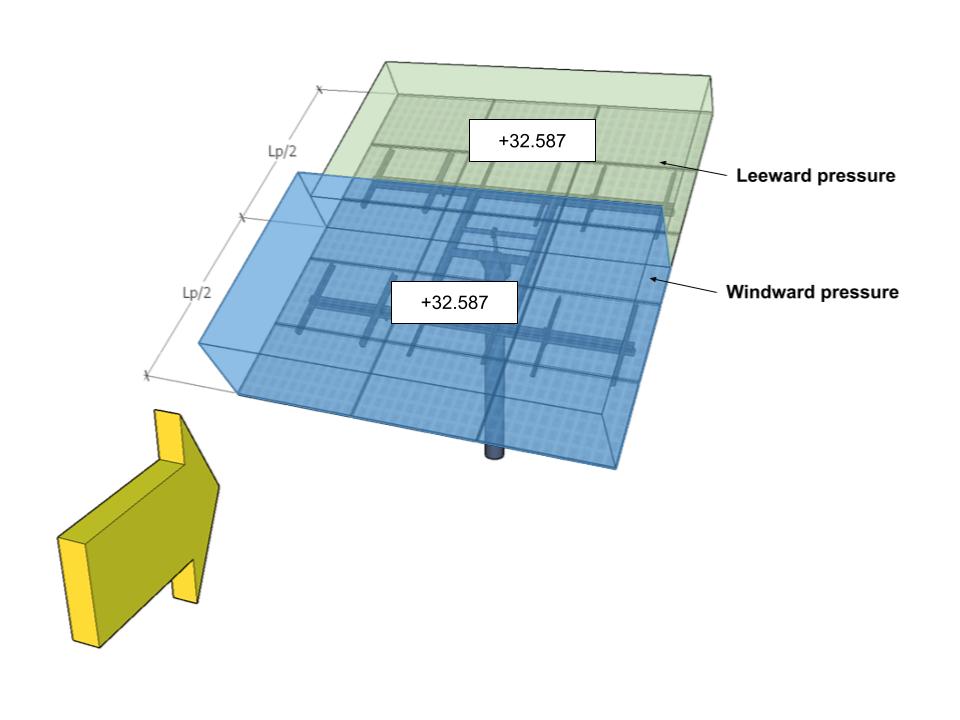
Abbildung 11. Auslegungswinddruck für Richtungswinkel 180° – Lastfall A.
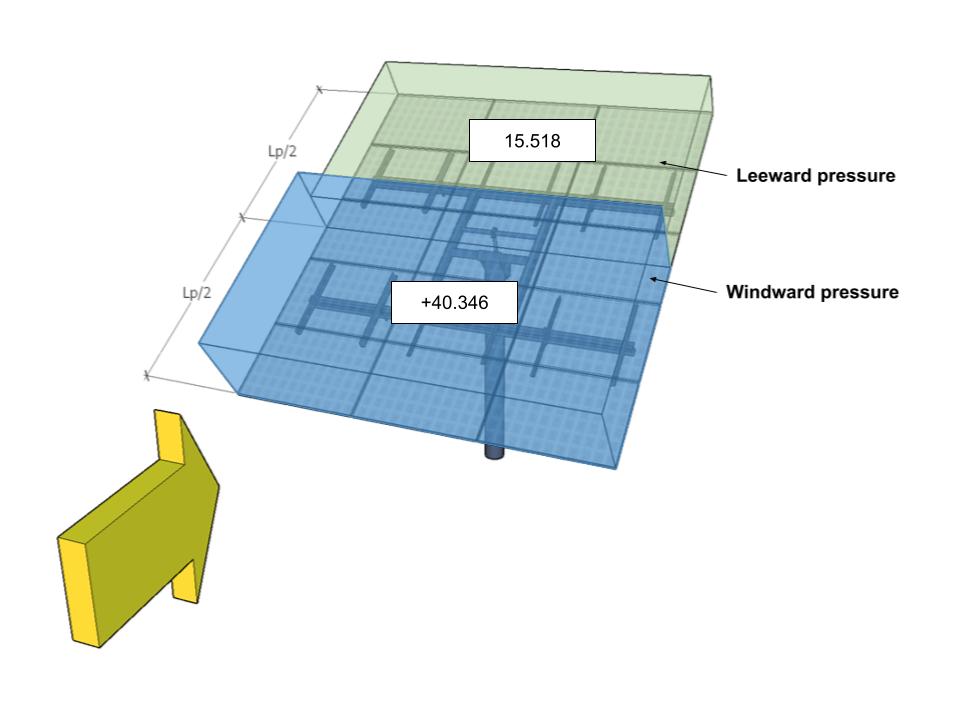
Abbildung 12. Auslegungswinddruck für Richtungswinkel 180° – Lastfall B.
Nettokraftkoeffizient, \({C}_{f}\), – Neigungswinkel > 45°
Nehmen wir an, dass der Neigungswinkel unseres Solarpanels geändert wurde 60°. Wir müssen die vertikale Projektion des Solarpanels verwenden und es als festes Zeichen betrachten, wobei der Geschwindigkeitsdruck bis zur Spitze dieser Projektion berechnet wird.
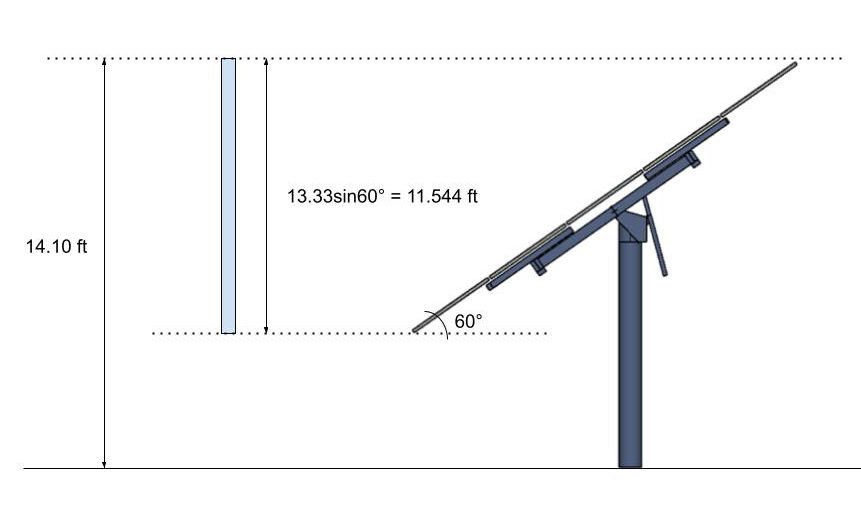
Abbildung 13. Die senkrechte Projektion des Solarpanels ist als solides Zeichen zu betrachten.
Da die Höhe vom Boden bis zur Spitze des Projekts immer noch geringer ist als 15 ft, Wir können immer noch unsere berechneten verwenden \( {K}_{z}\) über. Daher, der errechnete Wert von \( {q}_{h}\) wäre immer noch das gleiche. Das Netz für den Koeffizienten, \( {C}_{f}\), zu verwenden, können Sie der Abbildung entnehmen 29.3-1 von ASCE 7-16. Außerdem, bei der Berechnung dieser Kraftbeiwerte, Wir werden nur Fall A für einen vereinfachten Ansatz betrachten. Aus der Abbildung 29.3-1:
\({q}_{h} = 18.256 psf\)
\( B = 16.25 ft\)
\( s = 11.544 ft\)
\( h = 14.102 ft\)
\( s/h = 0.818\)
\( B/s = 1.408\)
Aus den tabellierten Werten von \( {C}_{f} \) in Abbildung 29.3-1, wir werden die bekannten Werte von interpolieren \( B/s \) gleich 1 und 2, und \( s/h \) gleich 0.9 und 0.7.
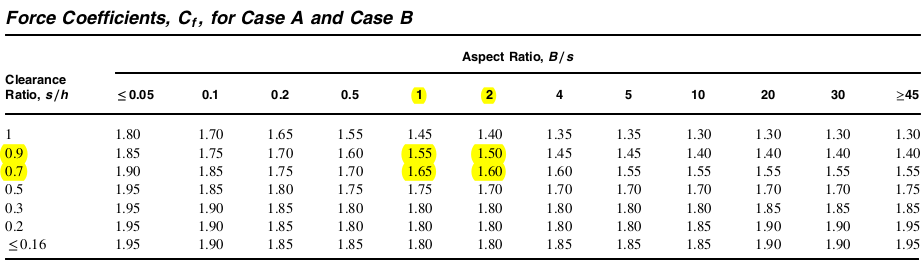
Abbildung 14. Nettokraftkoeffizient, \( {C.}_{f} \), Werte aus Abbildung 29.3-1 von ASCE 7-16 für solide Zeichen.
Durch Interpolieren erhält man die hervorgehobenen Werte \( {C}_{f} \) von unserer \( B/s \) und \( s/h \), ,:
\( {C}_{f} = 1.5706 \)
Design-Winddruck – Neigungswinkel > 45°
Bei der Berechnung der Windlast auf Sonnenkollektoren mit Neigungswinkel > 45°, Wir werden Gleichung verwenden (2), daher, die Windlasten auf Freiflächen-Solarpanels:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
\( {C}_{f} = 1.5706 \)
\(p = {q}_{h}G{C}_{f} = (18.256)(0.85)(1.5706) = 24.372 psf\)
\(p = 24.372 psf\)
Deshalb, die Windlasten auf bodenmontierte Solarmodule, wenn sie aufgebracht werden: 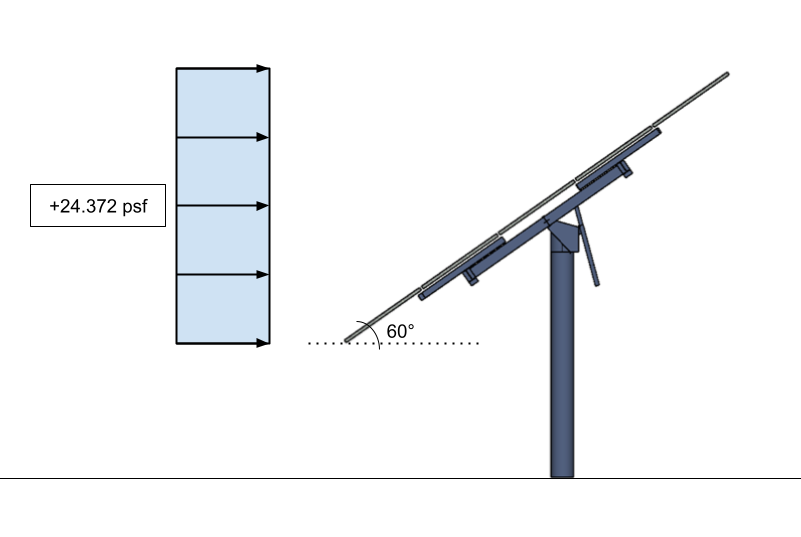
Abbildung 15. Der Auslegungswinddruck für das Solarpanel als solides Zeichen – auf die vertikale Projektion angewendet.
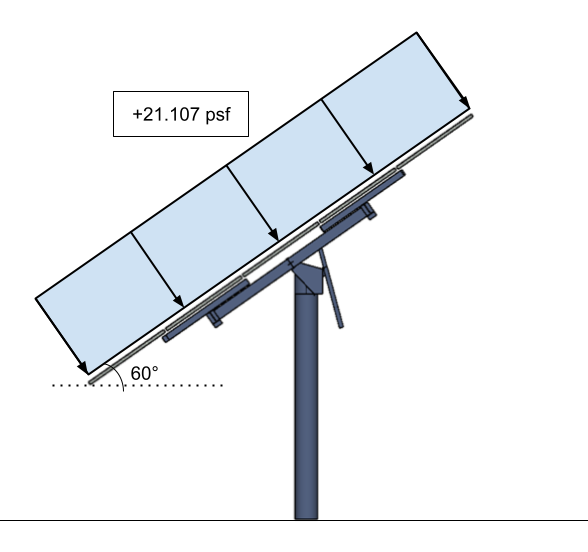
Abbildung 16. Der umgerechnete Auslegungswinddruck für das Solarpanel als solides Zeichen – auf die Oberfläche des Solarpanels aufgetragen.
Die Windberechnungen können alle mit dem SkyCiv Load Generator für ASCE durchgeführt werden 7-16 (Rechner für die Windlast von Solarmodulen). Benutzer können den Standort eingeben, um die Windgeschwindigkeit und Geländedaten zu erhalten, Geben Sie die Solarmodulparameter ein und generieren Sie die Auslegungswinddrücke. Mit der Standalone-Version, Sie können diesen Prozess rationalisieren und erhalten einen detaillierten Windlastberechnungsbericht für Solarmodule!
Schneebeladung
Für schneebedeckte Gebiete, Schneelasten auf dem Solarmodul sollten ebenfalls berücksichtigt werden. Um Schneelasten für unser Solarpanel zu berechnen, Wir werden Kapitel verwenden 7 von ASCE 7-16. Wir werden die Solarzellenstruktur als Gebäude mit geneigtem Dach betrachten wir betrachten nur die ausgeglichene Schneelast (Schneelast auf Schrägdächern). Die Formeln zur Bestimmung der Schneelast für unser Solarpanel lauten wie folgt:
Zur Berechnung der Flachdach-Schneelast \({p}_{f} \):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \) (7)
Wo:
\({C}_{e} \) = Belichtungsfaktor
\({C}_{t} \) = thermischer Faktor
\({I}_{s} \) = Wichtigkeitsfaktor für die Schneelast
\({p}_{g} \) = Schneelast am Boden, in psf
Zur Berechnung der Schneelast auf Schrägdächern \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \) (8)
Wo:
\({C}_{s} \) = Dachneigungsfaktor
\({p}_{r} \) = Regen-auf-Schnee-Zuschlagslast
Belichtungsfaktor, \({C}_{e} \)
Der Belichtungsfaktor, \({C}_{e} \), können aus der Tabelle ermittelt werden 7.3-1 von ASCE 7-16 basierend auf der Oberflächenrauheit und Exposition des Daches. Aus dem Satellitenbild des Standorts, das wir von Google Maps erhalten haben, Wir können klassifizieren, dass der Standort ist Oberflächenrauheit C (offenes Gelände mit vereinzelten Hindernissen, die im Allgemeinen weniger als hoch sind 30 ft) und mit der Annahme, dass die Sonnenkollektoren sind vollständig belichtet und ohne Hindernisse. Daher, bleibt die Belichtungsfaktor, \({C}_{e} \), der Struktur gleich ist 0.9.
Thermischer Faktor, \({C}_{t} \)
Der thermische Faktor, \({C}_{t} \), können aus der Tabelle ermittelt werden 7.3-2 von ASCE 7-16 basierend auf dem thermischen Zustand des Bauwerks im Winter. Vom Tisch, Wir können unser Solarpanel als klassifizieren “Unbeheizte und Open-Air-Strukturen.” Deshalb, das entsprechende von Thermischer Faktor, \({C}_{t} \), ist für die Struktur gleich 1.2.
Wichtigkeitsfaktor für die Schneelast, \({I}_{s} \)
Der Wichtigkeitsfaktor für die Schneelast, \({I}_{s} \), können aus der Tabelle ermittelt werden 1.5-2 von ASCE 7-16 basierend auf der Risikokategorie der Struktur. Da die Struktur in die Risikoklasse I eingestuft ist, vom Tisch, \({I}_{s} \) entspricht 0.8.
Grundschneelast, \({p}_{g} \)
Die Bodenschneelast, \({p}_{g} \), kann aus Abbildung bestimmt werden 7.2-1 von ASCE 7-16 Wie nachfolgend dargestellt. Von dieser Figur, bleibt die Bodenschneelast, \({p}_{g} \) für unser Solarpanel ist gleich 10 psf.
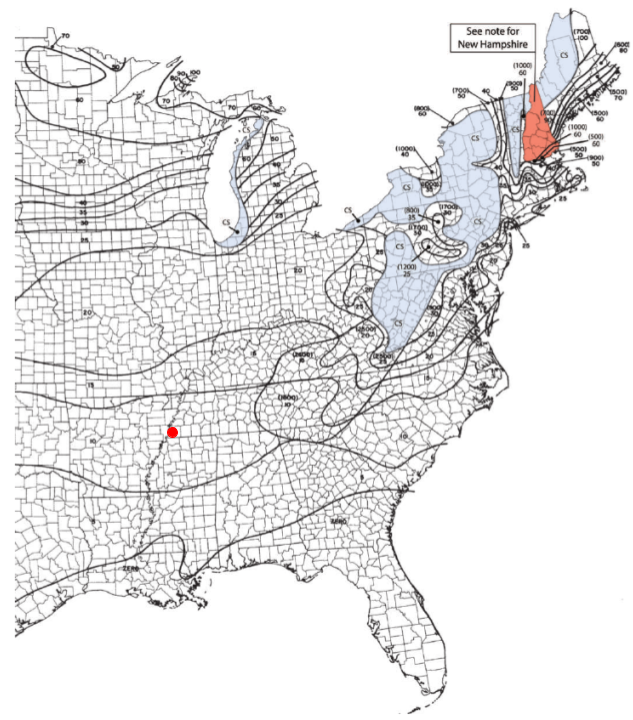
Abbildung 17. Bodenschneelastkarte aus Abbildung 7.2-1 von ASCE 7-16 mit rotem Punkt, um den Standort unseres Solarpanels anzuzeigen.
SkyCiv automatisiert auch die Bodenschneelastberechnungen mit einigen Parametern. Probier unser Rechner für die Windlast von Solarmodulen
Flachdach-Schneelast, \({p}_{f} \)
Aus den obigen Parametern, können wir bereits die Flachdach-Schneelast berechnen, \({p}_{f} \), unter Verwendung von Gleichung (7):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \)
\({p}_{f} = 0.7(0.9)(1.2)(0.8)(10) = 6.048 psf \)
\({p}_{f} = 6.048 psf \)
Dachneigungsfaktor, \({C}_{s} \)
Der Dachneigungsfaktor kann aus Abbildung berechnet werden 7.4-1 von ASCE 7-16 je nach Neigungswinkel, das Hindernis unterhalb der Dachfläche, und der Wert des thermischen Faktors \({C}_{t} \). Für unser Solarpanel, Wir gehen davon aus, dass unser Solarpanel als klassifiziert ist “Rutschige Oberfläche.” Da der thermische Faktor \({C}_{t} \) entspricht 1.2, wir können den Wert von bereits interpolieren \({C}_{s} \) von 7-2 c. Aus der Grafik, die bekannten Werte sind:
\({C}_{s} = 1.0 \) for 15°
\({C}_{s} = 0.0 \) for 70°
Durch Interpolation dieser Werte können wir erhalten:
\({C}_{s} = 0.727 \) for 30°
Deshalb, \({C}_{s} = 0.727 \) für unser Solarpanel.
Regen-auf-Schnee-Zuschlag, \({p}_{r} \)
Ein zusätzliches 5 psf Regen-auf-Schnee-Zuschlag laden, \({p}_{r} \), sollte für Standorte in Betracht gezogen werden, wo \({p}_{g} \) kleiner oder gleich ist 20 psf aber nicht null, für alle Dächer mit Neigungswinkel (in Grad) weniger als \( W/50 \) Grad wo \( W \) ist der horizontale Abstand von der Traufe zum First. Der Wert von \({p}_{r} \) gilt nur für das Schrägdach (ausgewogen) Lastfall. Für dieses Beispiel:
\(W = 13.33 cos 30° = 11.544 ft \)
\( W/50 =0.231° \)
Schon seit \({p}_{g} = 10 psf \) aber Neigungswinkel 30° ist größer als \( W/50 =0.231° \), \({p}_{r} \) kann vernachlässigt werden und ist gleich 0.0
Schrägdach Schneelast, \({p}_{s} \)
Aus der Gleichung (8), können wir die Schneelast für Schrägdächer berechnen \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \)
\({p}_{s} = (0.727)(6.048) + 0.0 = 4.397 psf \)
\({p}_{s} = 4.397 psf \)
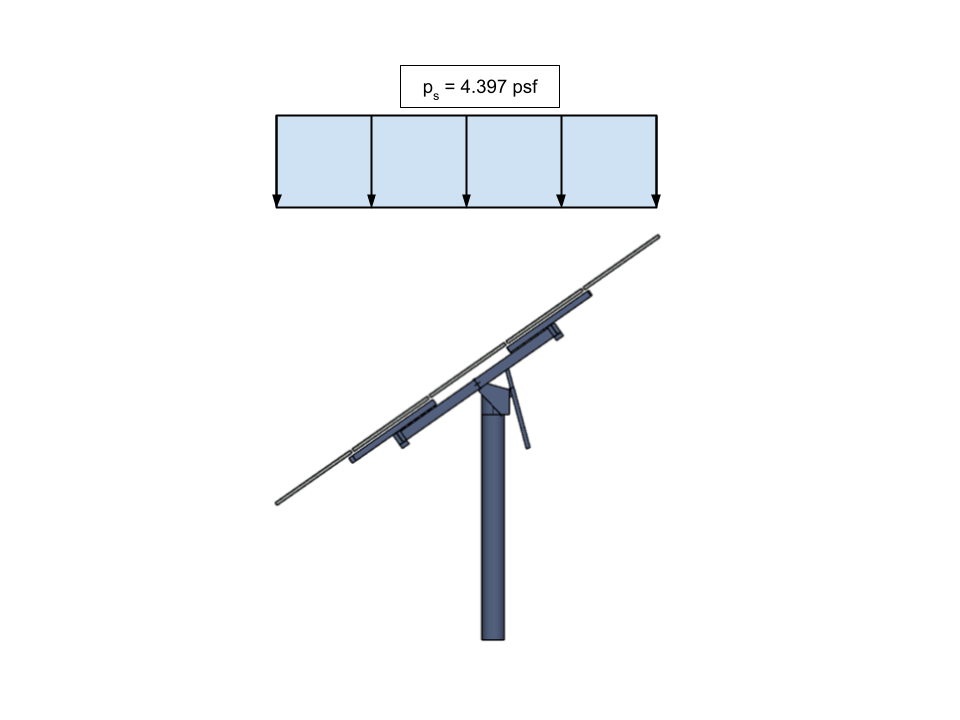
Abbildung 18. Die berechnete ausgeglichene Schneelast (Schneelast auf Schrägdächern) für das Solarpanel, das auf der horizontalen Projektion der Struktur angebracht ist.
Beachten Sie, dass \({p}_{s} \) wird auf die horizontale Projektion der Struktur angewendet. Wir müssen diesen Wert in eine äquivalente geneigte Drucklast umwandeln, damit wir ihn auf unser Modell anwenden können.
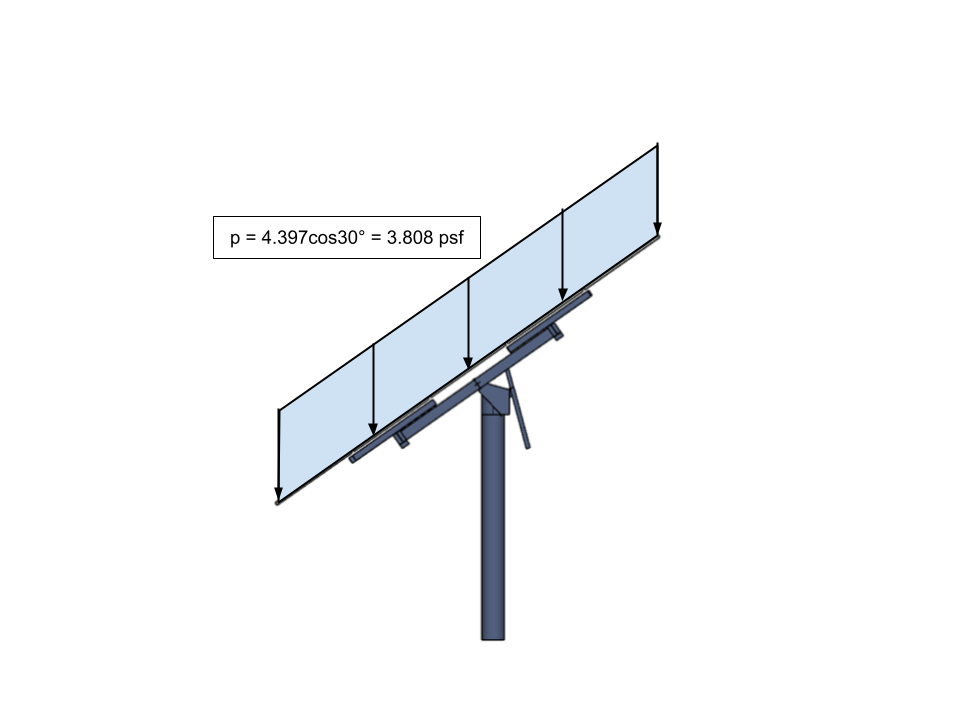
Abbildung 19. Die umgerechnete ausgeglichene Schneelast (Schneelast auf Schrägdächern) für das Solarpanel, das auf unser Modell angewendet werden soll.
Die Schneelastberechnungen können auch im SkyCiv Load Generator für ASCE durchgeführt werden 7-16. Jedoch, Es ist nur in unserer Standalone-Version und dem Professional Account verfügbar.
SkyCiv Lastgenerator
Verwenden des SkyCiv-Lastgenerators, Mit wenigen Klicks und Eingaben erhalten Sie Windlasten und Schneelasten auf Freiflächen-Solarmodulen. Wenn Sie die Standalone-Version kaufen oder sich für ein Professional-Konto anmelden, Sie können den detaillierten Wind- und Schneeberechnungsbericht für Ihr Solarmodulprojekt erstellen!
Sie können den detaillierten Wind- und Schneelastbericht für das Solarmodul über diese Links einsehen:
Außerdem, Sie können auch Ihren eigenen Windlastrechner für Solarmodule mit der SkyCiv Load Generator API erstellen, genau wie wir eine Lösung für einen unserer Kunden erstellt haben. Mit nur wenigen Eingaben, Es entwirft automatisch das Solarpanelsystem für Sie. Sie können unsere API-Dokumentation hierüber überprüfen link.
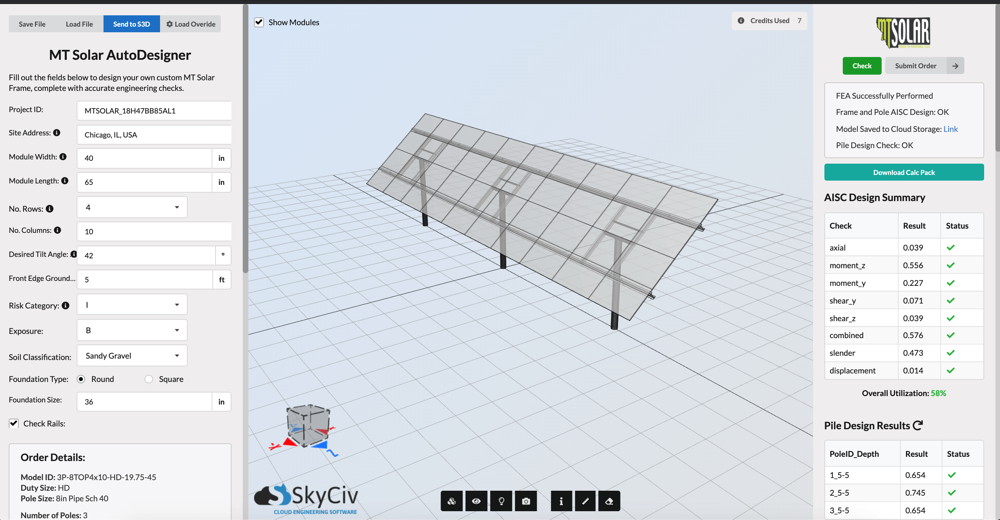
Abbildung 20. Unsere kundenspezifische Lösung für Solarmodule, die für MT Solar mithilfe der SkyCiv-API erstellt wurde.
Für zusätzliche Ressourcen, Sie können diese Links verwenden:
- Einführung in SkyCiv Load Generator
- ASCE 7-16 Windlastberechnungen (Solarplatten)
- ASCE 7 Schneelastberechnungen
- Berechnen und Anwenden von Dachschneeverwehungslasten mit ASCE 7-10
- Berechnung der Dachschneelasten mit ASCE 7-10
Statiker, Produktentwicklung
MS Bauingenieurwesen
Verweise:
- Coulbourne, W.. L. L., & Stafford, T.. E.. (2020, April). Windlasten: Leitfaden zu den Windlastbestimmungen von ASCE 7-16. Amerikanische Gesellschaft der Bauingenieure.
- Amerikanische Gesellschaft der Bauingenieure. (2017, Juni). Minimale Auslegungslasten und zugehörige Kriterien für Gebäude und andere Strukturen. Amerikanische Gesellschaft der Bauingenieure.
- Google Maps
- MT Solar



