Ein voll funktionsfähiges Beispiel für NBCC 2015 Schneelastberechnungen
Die Ansammlung von Schnee auf Bauwerken kann für Dachbauteile oder andere freiliegende Bauelemente sehr gefährlich sein. Das Nationales Baugesetz von Kanada (2015) Abteilung B. – Sektion 4.1.6 bietet eine detaillierte Berechnung der Schneelasten und der damit verbundenen Regenlasten. Verwendung dieser Richtlinie, Wir werden anhand eines Beispiels für strukturelles 3D zeigen, wie die Schneelasten berechnet werden (S3D) Lagermodell, Wie nachfolgend dargestellt:
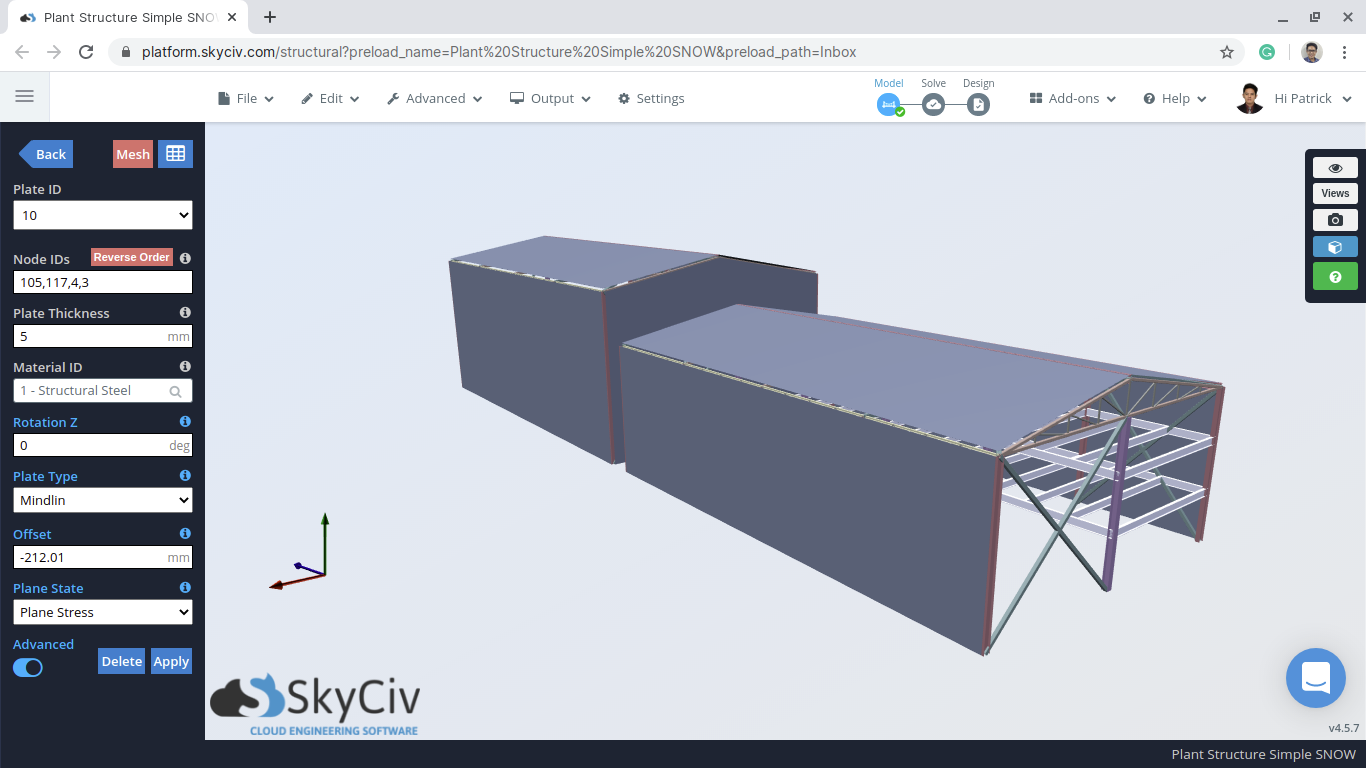
Zahl 1: Beispiel S3D-Lagermodell
Zahl 2: Beispiel für einen Standort mit Google Maps (Nur zur Veranschaulichung).
Tabelle 1: Gebäudedaten, die für unsere Schneelastberechnung benötigt werden.
| Ort | Ogden, Calgary, Alberta (Nur zur Veranschaulichung) |
| Belegung | Lagerung oder Lagerung von Materialien |
| Maße | 19.508 m x 31.70 m für jede Struktur Traufhöhe des kleineren Gebäudes 9.144 m Scheitelhöhe des kleineren Gebäudes 11.941 m Der Unterschied zwischen oberem und unterem Dach ist 3.50 m Dachneigungswinkel 16° |
| Weitere Details | Dach hat eine rutschige Oberfläche Lücke zwischen Strukturen ist 2.30 m |
Aus der Tabelle 1, die angegebene Schneelast, \(S ), kann mit der Formel berechnet werden:
\(S = {I}_{s}[{S.}_{s}{C.}_{b}{C.}_{w}{C.}_{s}{C.}_{ein} +{S.}_{r}]\) (1)
Wo:
\({I}_{s}\) = Wichtigkeitsfaktor für die Schneelast, Tabelle 4.1.6.2-A
\({S.}_{s}\) = 1-in-50 Jahre Bodenschneelast, kPa, Unterabschnitt 1.1.3
\({C.}_{b}\) = grundlegender Dachschneelastfaktor, 4.1.6.2 (2)
\({C.}_{w}\) = Windexpositionsfaktor basierend, 4.1.6.2 (3) und (4)
\({C.}_{s}\) = Steigungsfaktor, 4.1.6.2 (5), (6), und (7)
\({C.}_{ein}\) = Akkumulationsfaktor, 4.1.6.2 (8)
\({S.}_{r}\) = 1 in 50 Jahren damit verbundene Regenlast, kPa, Unterabschnitt 1.1.3, aber nicht größer als \({S.}_{s}{C.}_{b}{C.}_{w}{C.}_{s}{C.}_{ein}\)
Jeder Parameter wird in den folgenden Abschnitten einzeln untersucht. Die folgenden Schneelastfälle werden berechnet: ausgeglichene und unausgeglichene Schneelast auf jedem Dach (Wind normal zum Grat), sowie die auf dem unteren Dach erzeugte Drift unter Berücksichtigung der Ansammlung durch Gleiten.
Wichtigkeitsfaktor, \({I}_{s}\)
Das erste, was bestimmt wird, ist der Wichtigkeitsfaktor, \({I}_{s}\), welches mit gefunden wird Tabelle 4.1.6.2-A wie angegeben. Da es sich bei der Struktur um ein Lagergebäude handelt, das im Falle eines Versagens nur geringe direkte Auswirkungen auf das menschliche Leben hat, Die Wichtigkeitskategorie ist Niedrig. Außerdem, Die Berechnung erfolgt im endgültigen Grenzzustand (ULS). Also von Tabelle 4.1.6.2-A, \({I}_{s}\) entspricht 0.80.
| Wichtigkeitskategorie | Wichtigkeitsfaktor, \({I}_{s}\) | |
|---|---|---|
| ULS | SLS | |
| Niedrig | 0.8 | 0.9 |
| Normal | 1.0 | 0.9 |
| Hoch | 1.15 | 0.9 |
| Nach der Katastrophe | 1.25 | 0.9 |
Grundschneelast, \({S.}_{s}\), und zugehörige Regenlast, \(({S.}_{r})\)
Die Bodenschneelast, \({S.}_{s}\), und damit verbundene Regenlast, \(({S.}_{r})\), Werte sind in tabellarisch aufgeführt Anhang C, Abteilung B von NBCC 2015 je nach Standort und Provinz. Für dieses Beispiel, die entsprechende \({S.}_{s}\) und \(({S.}_{r})\) im Calgary, Alberta entspricht 1.10 kPa und 0.1 kPa, beziehungsweise.
Es fällt mir schwer, nach dem Bodenschnee und der damit verbundenen Regenlast für NBCC zu suchen 2015? Versuchen das SkyCiv Free Load Generator Tool um Ihre Suche zu beschleunigen und die entsprechenden zu erhalten \({S.}_{s}\) und \({S.}_{r}\) basierend auf dem Standort Ihrer Struktur.
Windexpositionsfaktor, \({C.}_{w}\)
Für den Windexpositionsfaktor, \({C.}_{w}\), es darf gleich sein 1.0 basierend auf 4.1.6.2 (3). Dieser Faktor kann noch reduziert werden, solange die Bedingungen in 4.1.6.2 (4) ist befriedigt. Für dieses Beispiel, \({C.}_{w}\) soll gleich sein 1.0 da der Standort kein offenes Gelände ist, das die Struktur vollständig dem Wind aussetzt.
Grundlegender Schneelastfaktor für das Dach, \({C.}_{b}\)
Der grundlegende Dachschneelastfaktor, \({C.}_{b}\), kann mit den folgenden Formeln berechnet werden, wie in verwiesen 4.1.6.2 (2):
\({C.}_{b} = 0.8\) (2) zum \({l}_{c} ≤ (70/{{C.}_{w}}^{2})\) und
\({C.}_{b} = (1/{C.}_{w}) [1 – (1 – 0.8{C.}_{w})exp(-0.01({l}_{c}{{C.}_{w}}^{2} – 70))] \) (3) zum \({l}_{c} > (70/{{C.}_{w}}^{2})\)
Wo:
\({l}_{c}\) = charakteristische Länge des oberen oder unteren Daches definiert als: \(2w -{w}^{2}/l )
\(l ) = größere Planabmessung des Daches
\(w\) = kleinere Planabmessung des Daches
Für dieses Beispiel,\(l ) und \(w\) entspricht 31.7 m und 19.51 m, beziehungsweise, daher, \({l}_{c}\) entspricht 27.01. Schon seit \({l}_{c}\) ist weniger als \((70/{1.0}^{2})\), der grundlegende Dachschneelastfaktor, \({C.}_{b}\), entspricht 0.8.
Steigungsfaktor, \({C.}_{s}\)
Die Berechnung des Steigungsfaktors ist \({C.}_{s}\) detailliert in 4.1.6.2 (5), (6), und (7) wird unten gezeigt.
Für ungehindertes rutschiges Dach:
\({C.}_{s} = 1.0\) zum \(α ≤ 15°\)
\({C.}_{s} = 0\) zum \(ein > 60°\)
\({C.}_{s} = (60° – ein)/45°\) zum \(15° < α ≤ 60°\)
Für andere Fälle:
\({C.}_{s} = 1.0\) zum \(α ≤ 30°\)
\({C.}_{s} = 0\) zum \(ein > 70°\)
\({C.}_{s} = (70° – ein)/40°\) zum \(30° < α ≤ 70°\)
Spezifisches Gewicht des Schnees, \(γ )
Das spezifische Gewicht des Schnees ist in angegeben 4.1.6.13 und wird als genommen:
\(γ = 0.43{S.}_{s} + 2.2 kN /{m}^{3} ≤ 4,0 kN /{m}^{3}\) (4)
Für dieses Beispiel, \(γ ) entspricht \(2.673 kN /{m}^{3}\).
Akkumulationsfaktor, \({C.}_{ein}\)
Akkumulationsfaktor, \({C.}_{ein}\), w w 4.1.6.2 (8). w.
Spezifizierte Schneelast, \(S )
In diesem Abschnitt, die angegebene Schneelast, \(S ), wird für die ausgeglichenen und drifteten Fälle berechnet.
Ausgeglichener / ungetriebener Fall
Für den ausgeglichenen / ungetriebenen Fall, das Akkumulationsfaktor \({C.}_{ein}\) entspricht 1.0. Außerdem, w \(α\) ist \(16°\) und die Dachfläche wird als ungehindert rutschig angenommen, der Steigungsfaktor, \({C.}_{s}\), für unser Beispiel ist gleich 0.978. Gleichung verwenden (1), die angegebene Schneelast, \(S ), für ausgeglichenen / ungetriebenen Fall ist:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
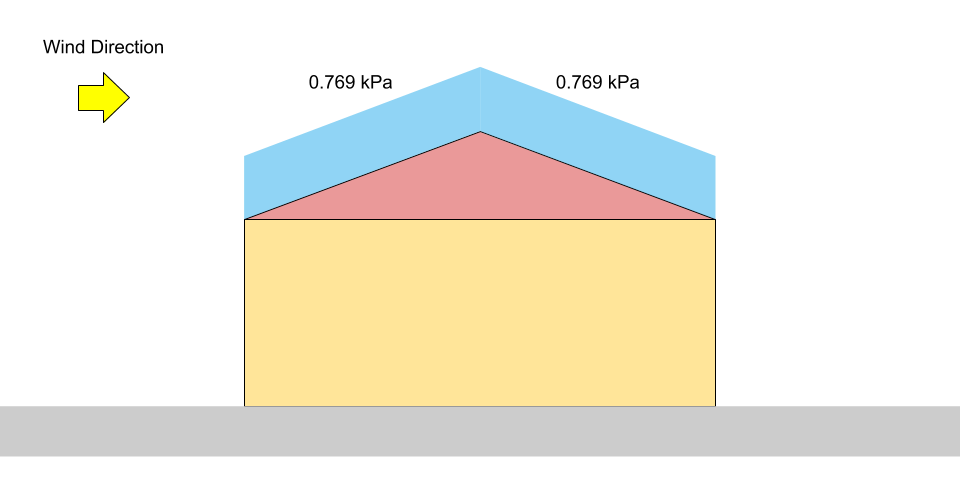
Zahl 3: Lastdiagramm für ausgeglichene Schneelast auf einem Satteldach.
Unausgeglichener / drifteter Fall
Wind wirkt normal auf Ridge
Da die Strukturen Satteldächer haben, die unausgeglichene Schneelast (Wind wirkt normal auf den Grat) Akkumulationsfaktor \({C.}_{ein}\) wird mit gefunden 4.1.6.9:
\({C.}_{ein, gegen den Wind} = 0\)
\({C.}_{ein, gegen den Wind} = 0.25 +α/20\) zum \(15° ≤ α ≤ 20°\)
\({C.}_{ein, gegen den Wind} = 1.25\) zum \(20° < α ≤ 90°\)
Weil beide Strukturen einen Dachneigungswinkel von 16 ° haben, die Akkumulationsfaktoren \({C.}_{ein, gegen den Wind}\) und \({C.}_{ein, gegen den Wind}\) sind gleich 0 und 1.05, beziehungsweise. Außerdem, w \(α\) ist \(16°\) und die Dachfläche wird als ungehindert rutschig angenommen, der Steigungsfaktor, \({C.}_{s}\), für unser Beispiel ist gleich 0.978.
Im unausgeglichenen / drifteten Fall normal zum Grat, \({C.}_{ein}\) wird berechnet auf der Grundlage von 4.1.6.9 für einen Satteldachkoffer. Aus der obigen Berechnung, \({C.}_{ein, gegen den Wind} = 0\) und \({C.}_{ein, gegen den Wind} = 1.05\). Daher, Die angegebenen Schneelasten für jede Seite sind:
\({S.}_{gegen den Wind} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S.}_{gegen den Wind} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)
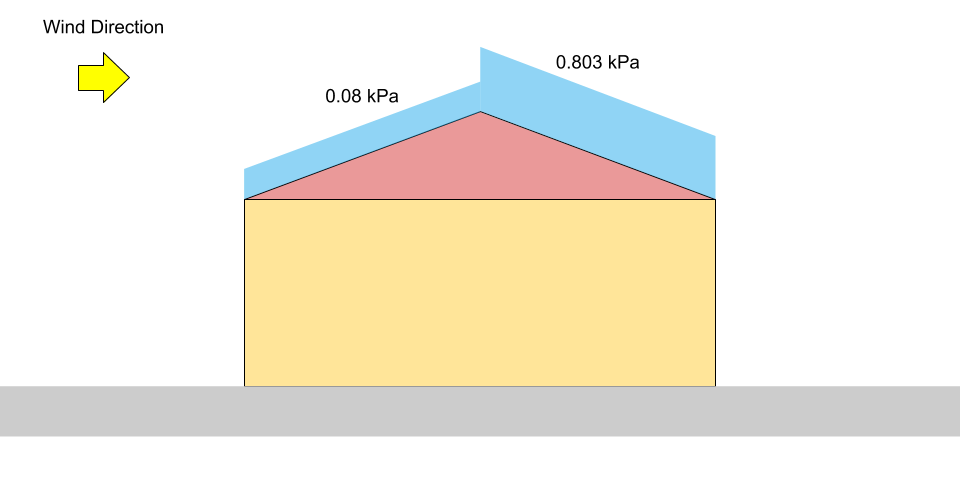
Zahl 4: Lastdiagramm für unausgeglichene Schneelast auf einem Satteldach (nicht maßstabsgetreu).
Wind wirkt parallel zum Grat – Fall I. – Wind vom oberen zum unteren Dach
Wenn der Wind parallel zum Grat wirkt, Auf dem unteren Dach wird höchstwahrscheinlich eine Schneeverwehung auftreten. w Akkumulationsfaktor \({C.}_{ein}\), die folgenden Formeln aus 4.1.6.2 (8) werden verwendet:
\({C.}_{ein} ={C.}_{a0} – ({C.}_{a0} – 1)(x /{x}_{d})\) zum \(0 ≤ x ≤ {x}_{d}\)
\({C.}_{ein} = 1.0\) zum \(x > {x}_{d}\)
Wo:
\({C.}_{a0}\) = Spitzenwert von \({C.}_{a0}\) bei x = 0
\(x ) = Abstand von der Dachstufe
\({x}_{d}\) = Driftlänge wie in Abbildung gezeigt 3 unten
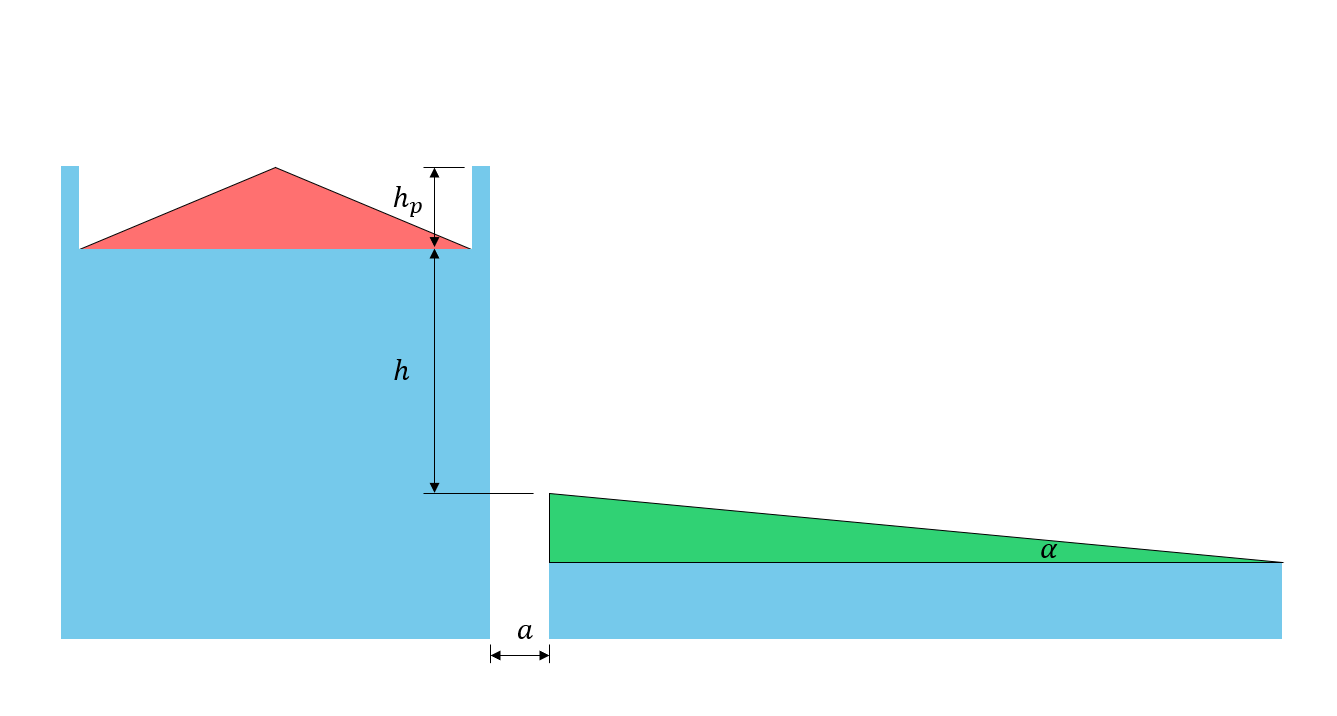
Zahl 5: Darstellung der Dachabmessungsparameter
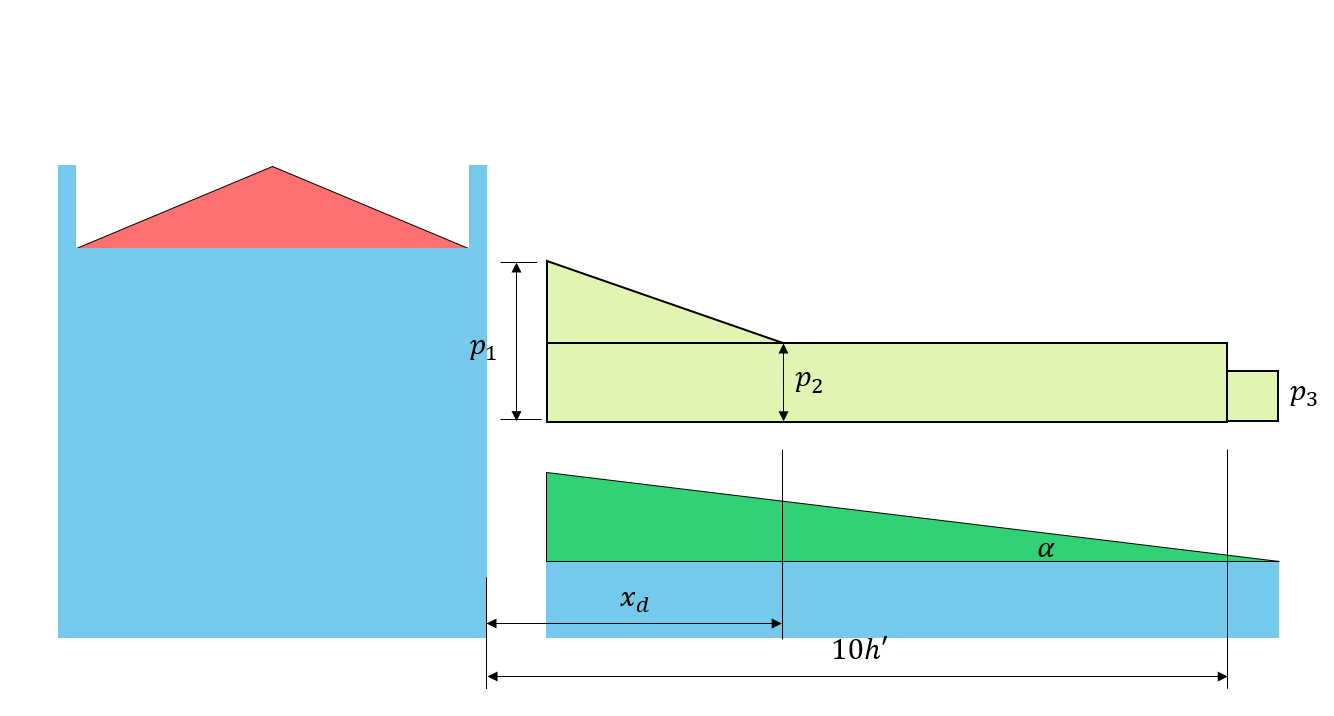
Zahl 6: Entsprechende Driftlast auf dem unteren Dach basierend auf Abbildung 4.1.6.5-A.
\({C.}_{a0}\) und \({x}_{d}\) kann mit den folgenden Formeln berechnet werden:
\({C.}_{a0} = frac{βγh}{{C.}_{b}{S.}_{s}}\) oder \({C.}_{a0} = frac{F.}{{C.}_{b}}\) (5), was auch immer geringer ist
\({x}_{d} = 5 \frac{{C.}_{b}{S.}_{s}}{γ }({C.}_{a0} – 1)\) (6)
\(F = 0.35β\sqrt{\frac{γ ({l}_{cs} – 5{{h}_{p}}^{„})}{{S.}_{s}}} +{C.}_{b}\) aber \(F ≤ 5\) zum \({C.}_{ws} = 1.0\) (7)
\({h}^{„} = h – \frac{{C.}_{b}{C.}_{w}{S.}_{s}}{γ }\) (8)
\({{h}_{p}}^{„} ={h}_{p} – \frac{0.8{S.}_{s}}{γ }\) aber \(0 ≤ {{h}_{p}}^{„} ≤ \frac{{l}_{cs}}{5}\) (9)
Wo:
\({h}_{p}\) = Höhe der Brüstung auf dem oberen Dach (0 in diesem Fall gibt es keine Brüstung)
\(h ) = Höhenunterschied zwischen oberer und unterer Dachebene
\({C.}_{ws}\) = Wert von \({C.}_{w}\) anwendbar auf die Quelle des Driftens
\({l}_{cs}\) = charakteristische Länge des Quellgebiets definiert als: \(2{w}_{s} -{{w}_{s}}^{2}/{l}_{s}\)
\({l}_{s}\) = größere Planabmessung des Quellbereichs wie in Abbildung gezeigt 7 und 8, unten gezeigt
\({w}_{s}\) = kleinere Planabmessung des Quellbereichs wie in Abbildung gezeigt 7 und 8, unten gezeigt
\(β ) = 1.0 für Fall I., und 0.67 für Fall II und III.
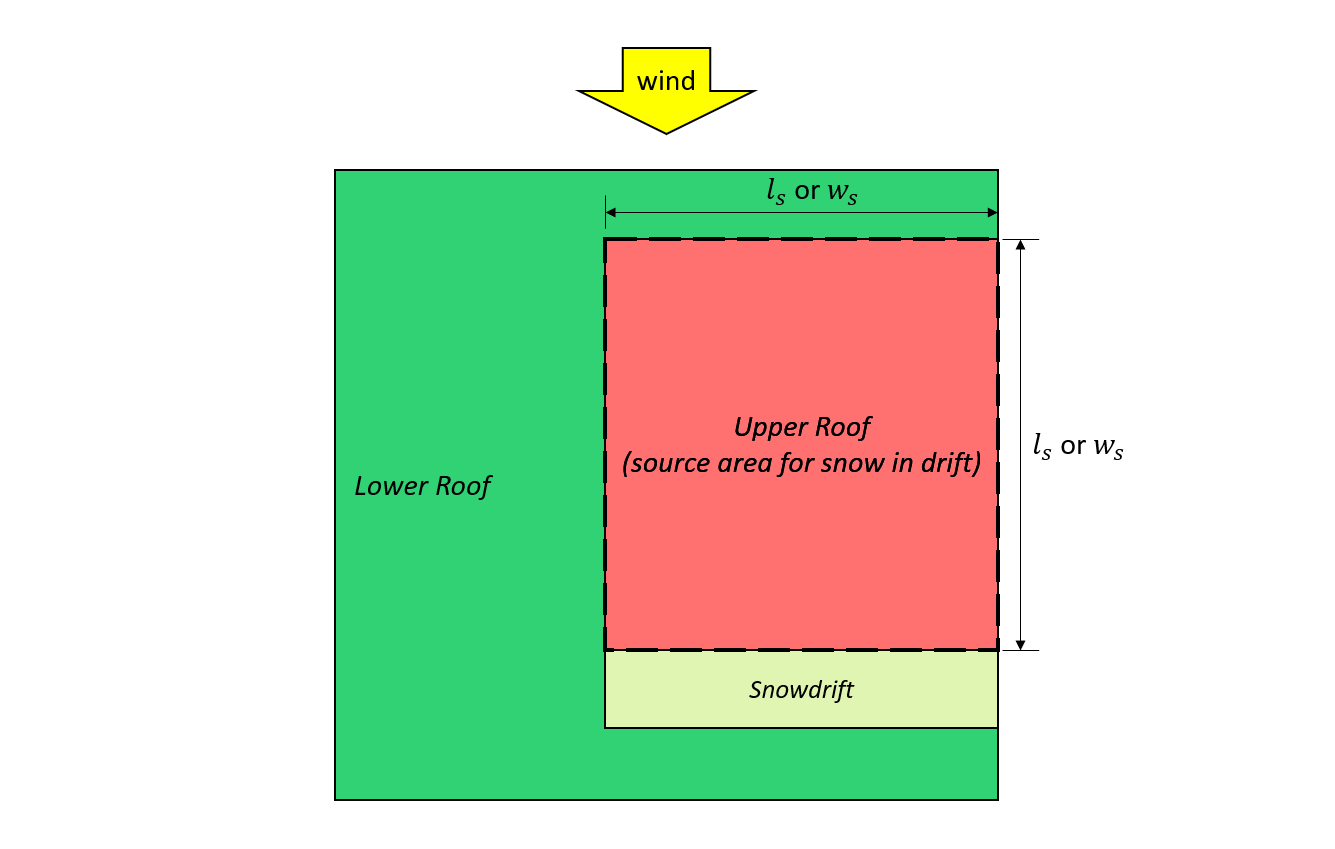
Zahl 7: Fall I. – Schneeverwehung gebildet aus dem Wind vom oberen Dach basierend auf Abbildung 4.1.6.5-B.
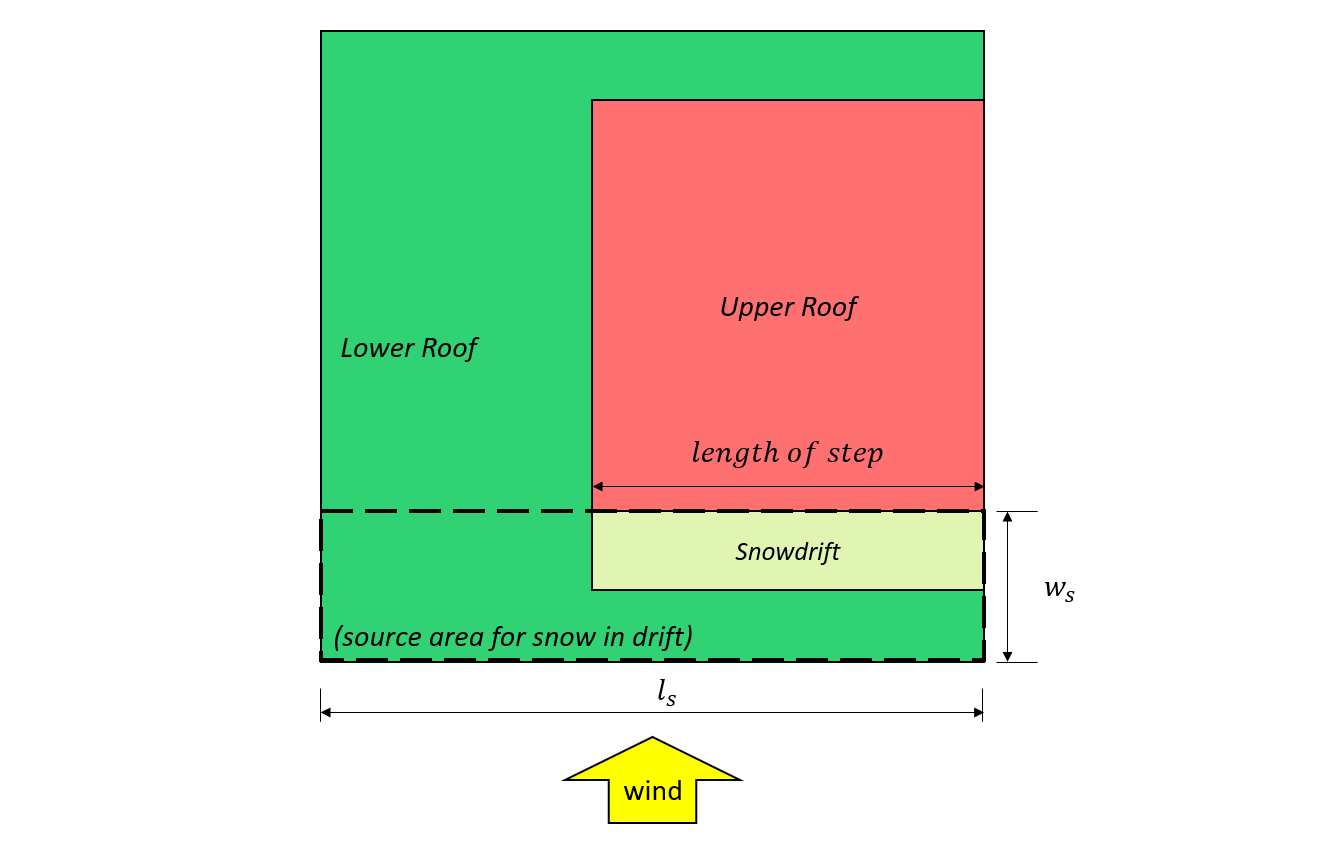
Zahl 8: Fall II – Schneeverwehung gebildet aus dem Wind vom unteren Dach basierend auf Abbildung 4.1.6.5-B.
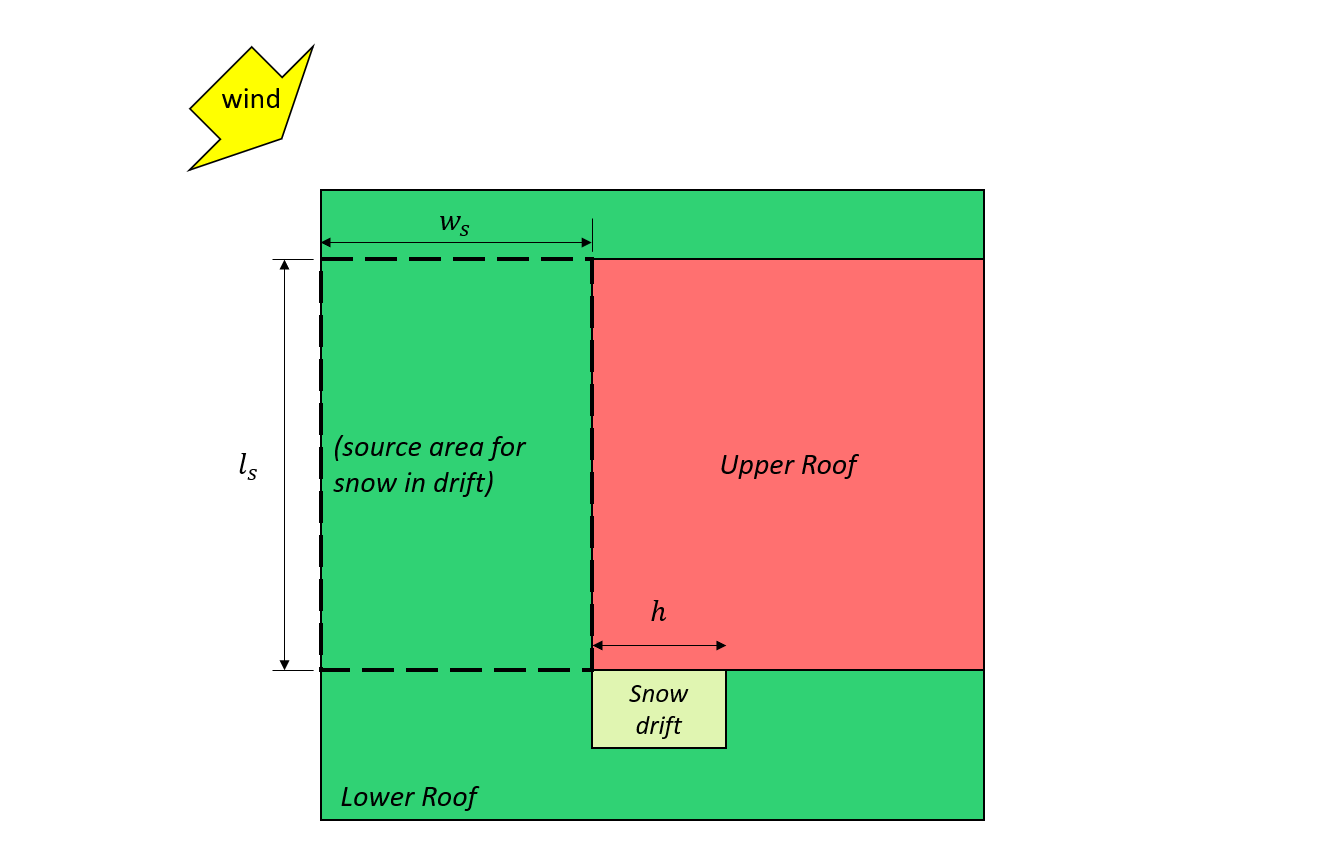
Zahl 7: Fall III – Teilschneeverwehung gebildet durch den Wind vom unteren Dach basierend auf Abbildung 4.1.6.5-B.
Für dieses Beispiel, Die Fälle I und II werden berücksichtigt.
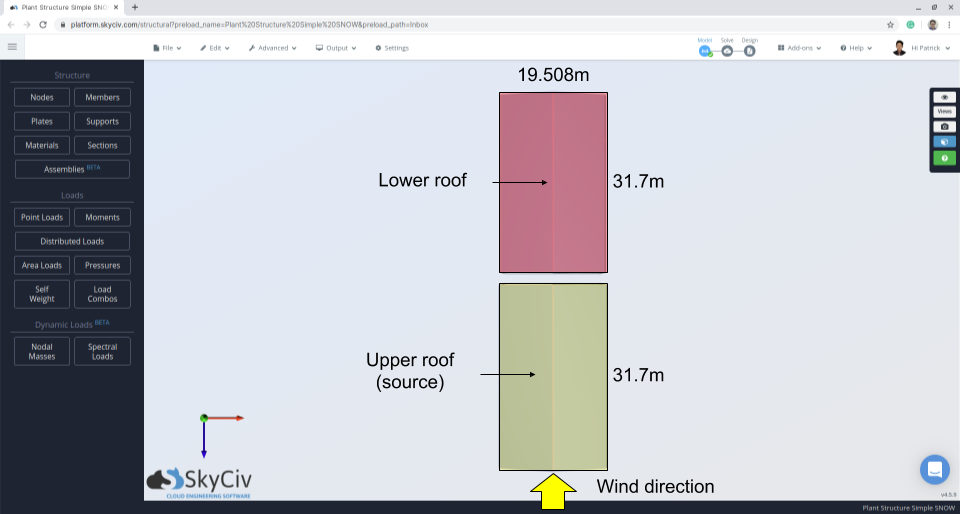
Zahl 10: Strukturplan mit Angabe der Windrichtung und des Quellgebiets.
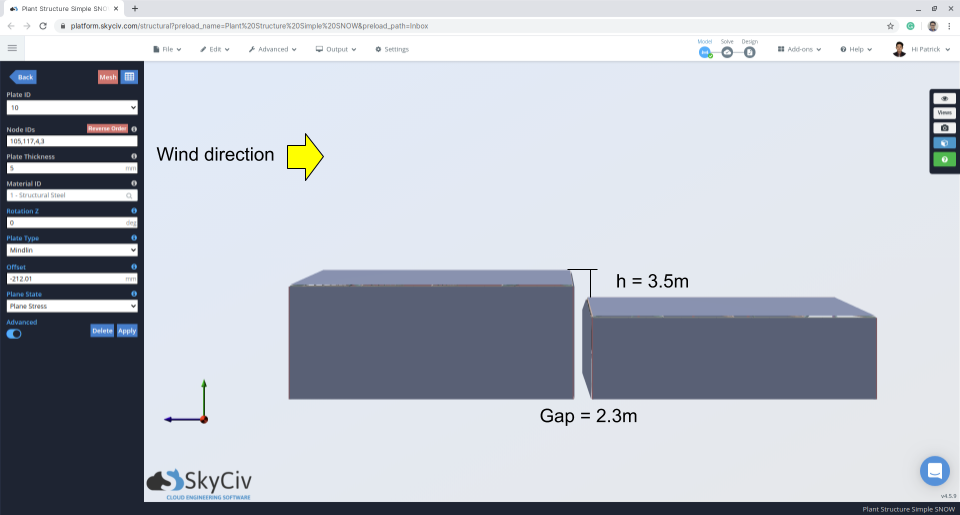
Zahl 11: Die Ansicht zeigt die Lücke und den Unterschied zwischen oberem und unterem Dach.
Für den unausgeglichenen / drifteten Fall parallel zum Grat, \({C.}_{ein}\) wird für Fall I und Fall II auf der Grundlage von berechnet 4.1.6.5 für das mehrstufige Dach. Für Fall I., Diese folgenden Parameter sollten zuerst unter Verwendung der verschiedenen zuvor in diesem Beispiel erwähnten Gleichungen berechnet werden:
\(β = 1.0\)
\({h}^{„} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m )
\({h}_{p} = 0\)
\({{h}_{p}}^{„} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m )
\(F = 0.35(1.0)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C.}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) oder \({C.}_{a0} = frac{3.66}{0.8} = 4.544\)
\({C.}_{a0} = 4.544\)
\({x}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 m )
Aus diesen Parametern, der Akkumulationsfaktor, \({C.}_{ein}\), kann durch Ersetzen des Wertes von berechnet werden \({C.}_{a0}\) bei jedem \(x ) Entfernung. Beachten Sie, dass wir berechnen müssen \({C.}_{ein}\) beim \(x = a ) wo \(ein) ist der Spalt zwischen dem Dach, da der Dachspalt kleiner als ist 5 m wie in angegeben 4.1.6.6.
beim \(x = 0\): \({C.}_{ein} = 4,544 – (4.544 – 1)(0/5.835) = 4.544\)
beim \(x = a ): \({C.}_{ein} = 4,544 – (4.544 – 1)(2.3/5.835) = 3.147\)
beim \(x = {x}_{d}\): \({C.}_{ein} =1.0\)
beim \(x = 10{h}^{„}\): \({C.}_{ein} =1.0\)
w w w, \({C.}_{s} = 1.0\). Außerdem, beim Auffinden der angegebenen Schneelast auf dem oberen Dach, der Akkumulationsfaktor, \({C.}_{ein}\), und Steigungsfaktor, \({C.}_{s}\), sind beide gleich 1.0. Daher, Die Größe der angegebenen Schneelasten an jedem Standort beträgt:
beim \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa\)
beim \(x = a ): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
beim \(x = {x}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
auf der oberen Dachebene: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)
Wind wirkt parallel zum Grat – Fall II – Wind vom unteren zum oberen Dach
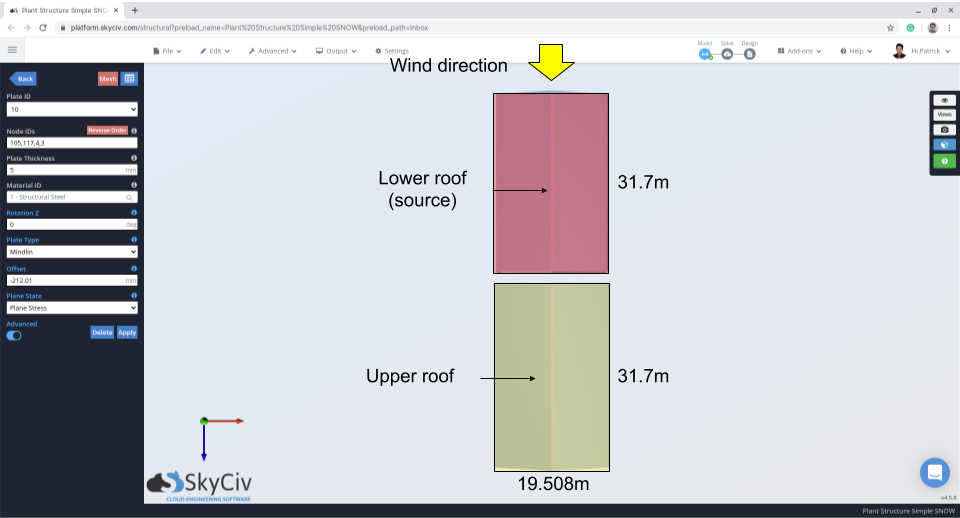
Zahl 12: Strukturplan mit Angabe der Windrichtung und des Quellgebiets – Wind vom unteren Dach zum oberen.
Für Fall II, Die Berechnung ist ähnlich wie in Fall I, hat jedoch eine andere \(β = 0.67\):
\(β = 0.67\)
\({h}^{„} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m )
\({h}_{p} = 0\)
\({{h}_{p}}^{„} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m )
\(F = 0.35(0.67)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C.}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) oder \({C.}_{a0} = frac{2.70}{0.8} = 3.375\)
\({C.}_{a0} = 3.375\)
\({x}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 m )
beim \(x = 0\): \({C.}_{ein} = 3,375 – (3.375 – 1)(0/3.909) = 3.375\)
beim \(x = a ): \({C.}_{ein} = 3,375 – (3.375 – 1)(2.3/3.909) = 1.978\)
beim \(x = {x}_{d}\): \({C.}_{ein} =1.0\)
beim \(x = 10{h}^{„}\): \({C.}_{ein} =1.0\)
beim \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa\)
beim \(x = a ): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
beim \(x = {x}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
auf der oberen Dachebene: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)
Zur Veranschaulichung, die entsprechende \({p}_{1}\), \({p}_{2}\), und \({p}_{3}\) sind in den Figuren gezeigt 13 und 14 unten für beide Fälle I und II, beziehungsweise.
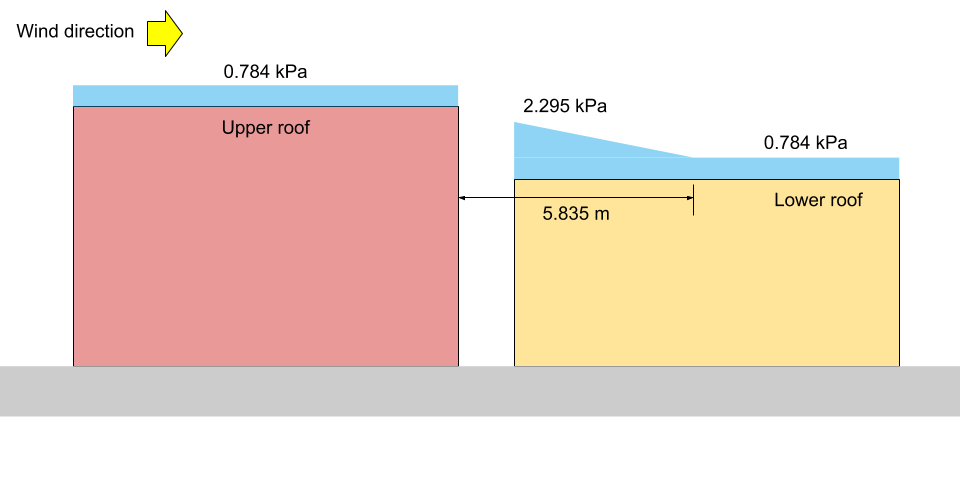
Zahl 13: Schneelastillustration für Fall I. (nicht maßstabsgetreu).
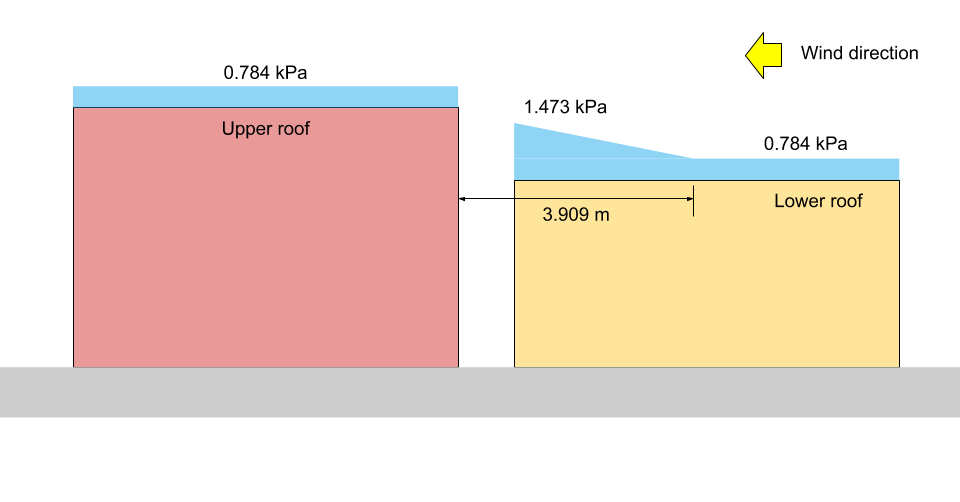
Zahl 14: Schneelastabbildung für Fall II (nicht maßstabsgetreu).
Führen Sie diese Berechnungen automatisch in Minuten durch
Das war eine lange Berechnung, Was können Sie als Ingenieur tun, um diesen Prozess für Ihre zukünftigen Projekte zu beschleunigen?? Vor kurzem hat SkyCiv den Schneelastgenerator als Teil des SkyCiv-Lastgenerators veröffentlicht und automatisiert, das kann auch Windlasten erzeugen. Um die Schneelasten des gezeigten Beispiels zu finden, Mit dem Tool sind nur ein paar Klicks erforderlich:
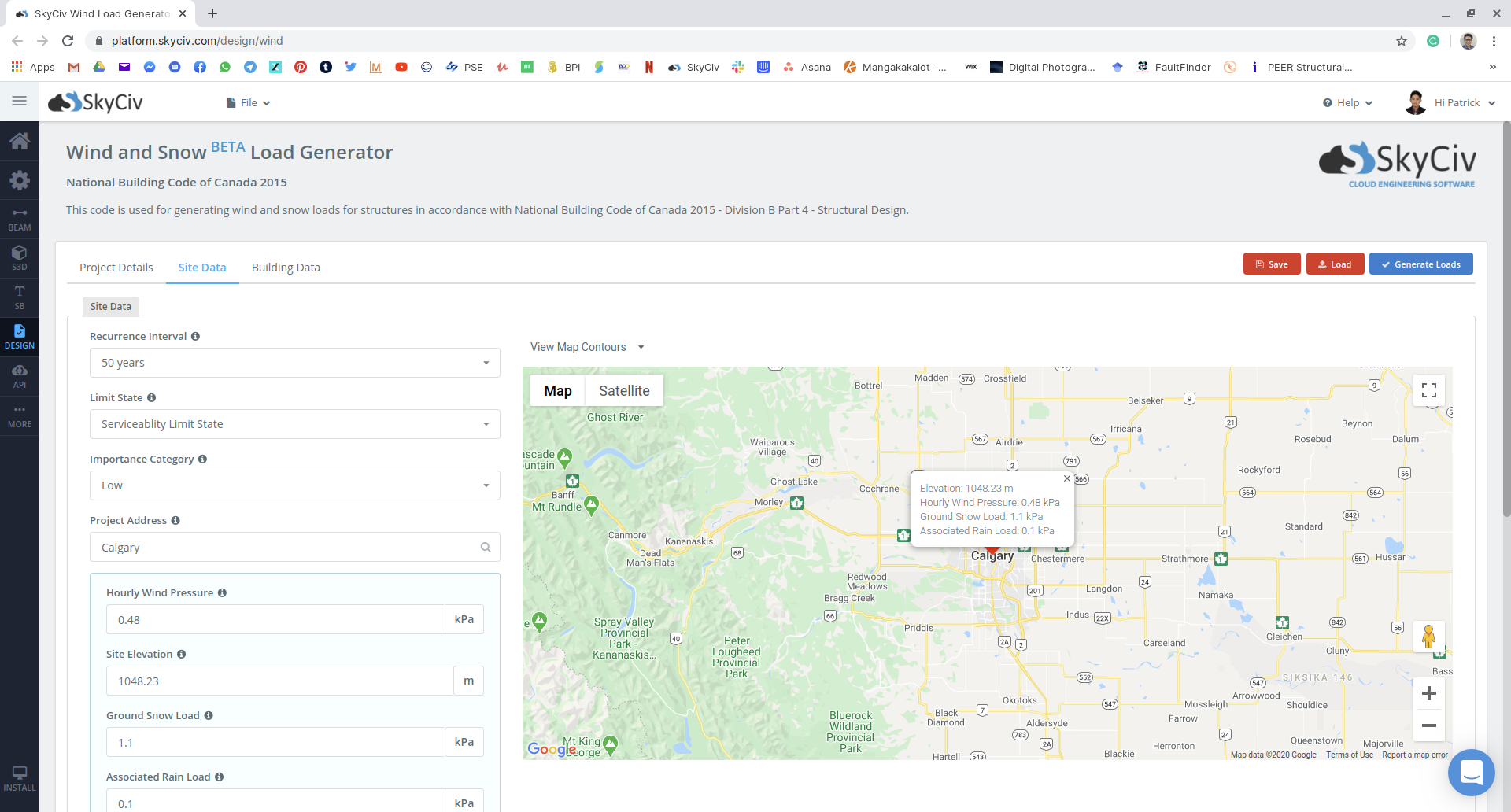
Zahl 15: Standortdateneingabe auf dem SkyCiv Load Generator-Modul anhand unseres Beispiels.
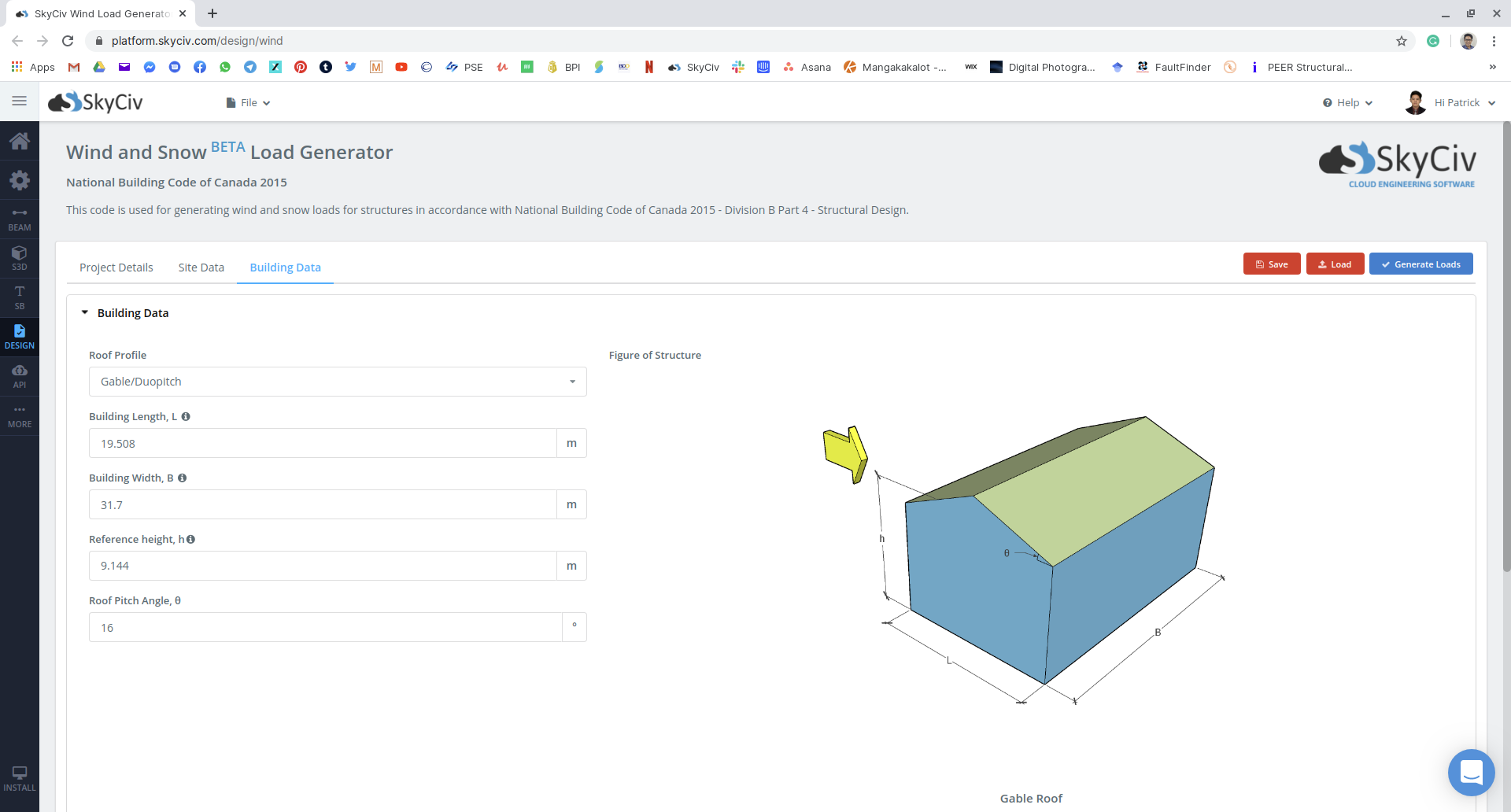
Zahl 16: Eingabe von Gebäude- und Schneeparametern am SkyCiv Load Generator-Modul anhand unseres Beispiels.
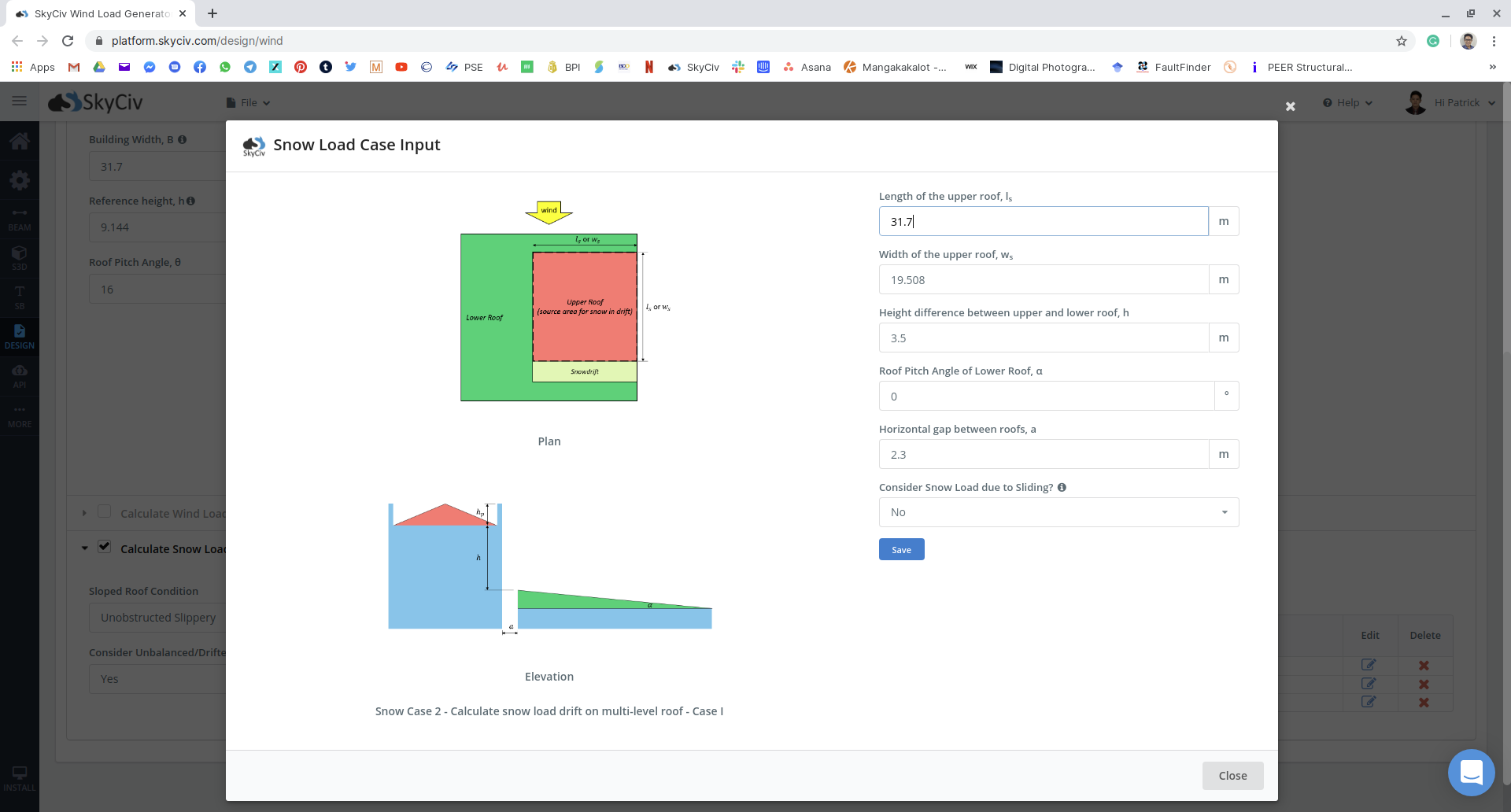
Zahl 17: Schneelasteingabe für mehrere unausgeglichene Fälle für das Beispiel.
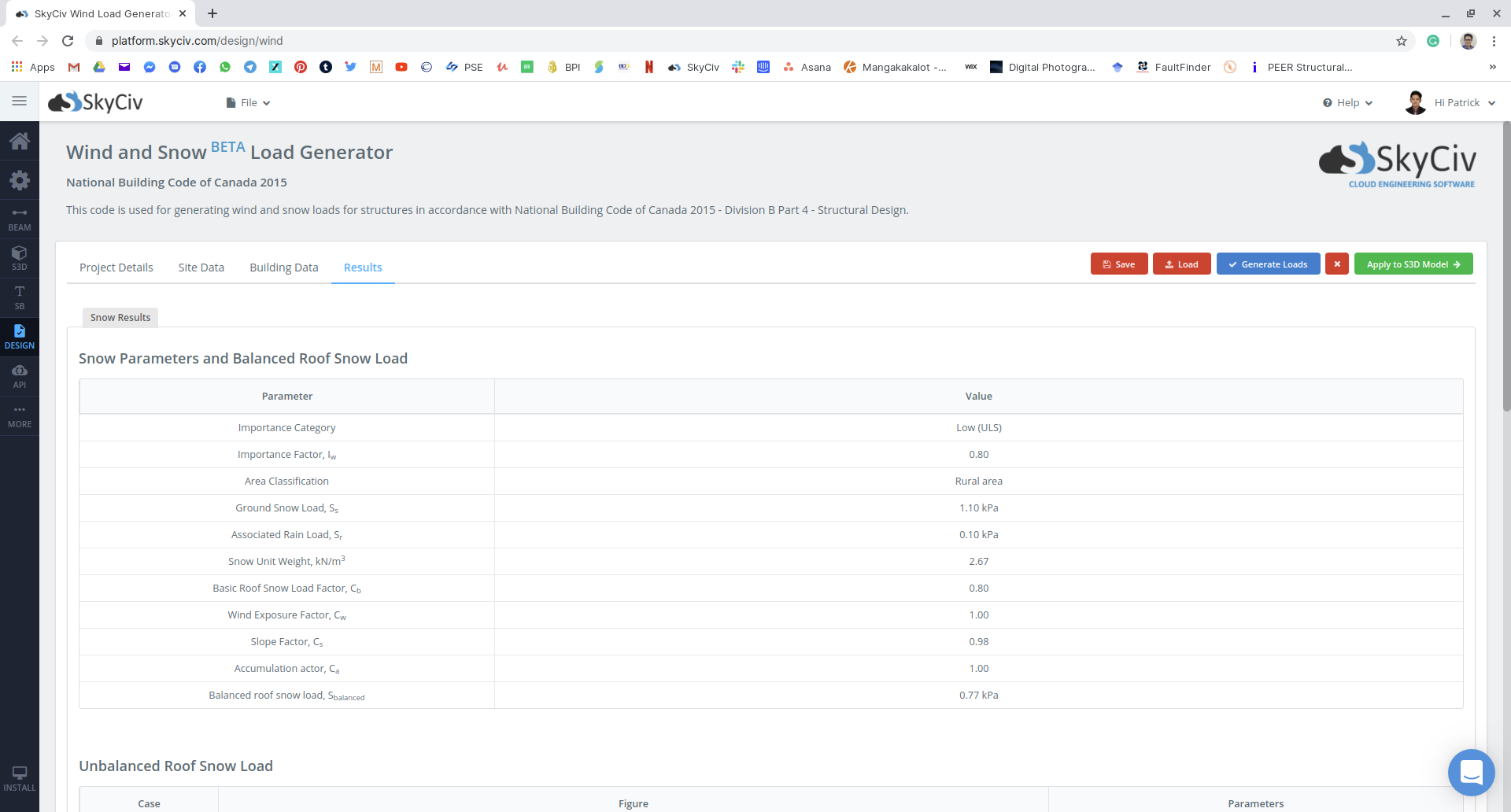
Zahl 18: Zusammenfassung der verwendeten Schneelastparameter und der ausgeglichenen Schneelast, die auf die Struktur angewendet werden soll.
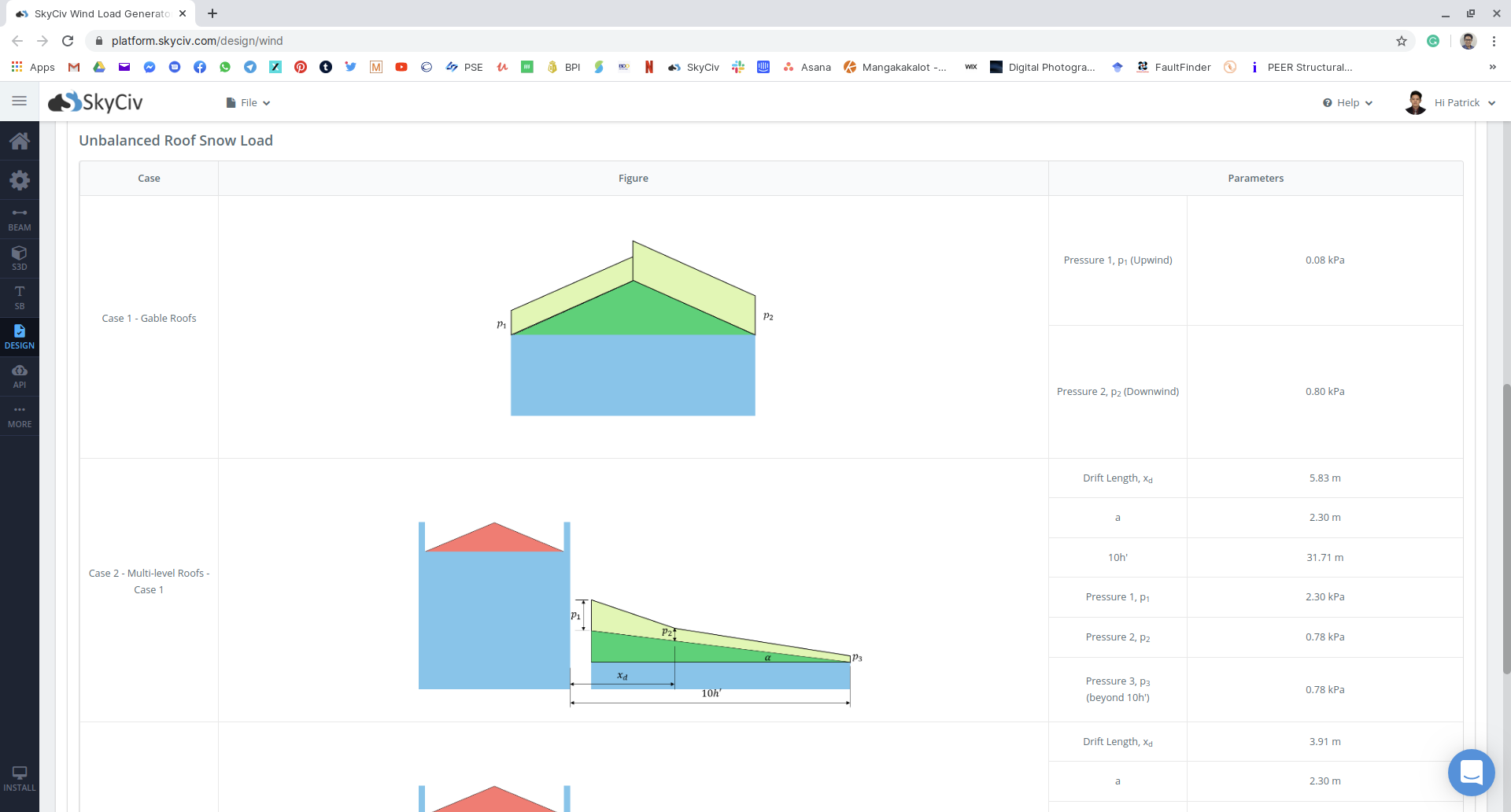
Zahl 19: Zusammenfassung der Ergebnisse der unausgeglichenen Schneelast.
Schneelastberechnungen im SkyCiv Load Generator-Modul werden durch Referenzcodes wie ASCE unterstützt 7-10, 7-16, IM 1991-1-3, NBCC 2015, und AS / NZS 1170.3, und ist auf der verfügbar Eigenständige (Nur Generator laden) und Fachmann Konten. Mit Programmierung und APIs vertraut? Diese Funktionalität kann mit dem automatisiert werden SkyCiv API.
Statiker, Produktentwicklung
MS Bauingenieurwesen
Verweise:
- Nationaler Forschungsrat von Kanada. (2015). Nationales Baugesetz von Kanada, 2015. Nationaler Forschungsrat von Kanada.
Hinweis:
- NBCC-Code-Referenz für die “Grundlegender Schneelastfaktor für das Dach” — suchen 4.1.6.2 Satz (2)
- NBCC-Code-Referenz für die “Windexpositionsfaktor” — suchen 4.1.6.2 Sätze (3) und (4)
- NBCC-Code-Referenz für die “Steigungsfaktor” — suchen 4.1.6.2 Sätze (5), (6), und (7)
- NBCC-Code-Referenz für die “Akkumulationsfaktor” — suchen 4.1.6.2 Satz (8), 4.1.6.5 für mehrstufige Dächer, 4.1.6.6 für Dächer mit Spalt, und 4.1.6.9 für Satteldächer
