Der SkyCiv-Lastgenerator hat kürzlich die Berechnung der seismischen Last gemäß ASCE7-16 hinzugefügt. Dies beinhaltet die Integration der seismischen USGS-Daten und deren Verarbeitung, um die seismische Basisscherung mit Abschnitt zu generieren 12.8 Äquivalentes laterales Verfahren. In diesem Artikel, Wir werden tiefer in den Prozess der Berechnung der seismischen Lasten für ein Gebäude mit ASCE eintauchen 7-16.
SkyCiv hat jetzt die seismischen Daten der Website von der USGS-Web-API integriert. Probier unser SkyCiv Lastgenerator!
Strukturdaten
In diesem Beispiel, Wir werden die folgenden Daten zur Berechnung der seismischen Belastung verwenden:
Tabelle 1. Gebäudedaten, die für unsere Erdbebenlastberechnung benötigt werden.
| Ort | 8050 SW Beaverton Hillsdale Hwy, Portland, ODER 97225, USA |
| Belegung | Wohnhaus |
| Maße | 64 ft (4 Buchten) × 104 ft (6 Buchten) Im Plan Bodenhöhe 15 ft Dachhöhe bei elev. 75 ft Flachdach Spalte: 20″x20″ Strahl: 14″x20″ Platte: 8″ Dicke |
| Wird geladen | Gewicht der konkreten Einheit : 156 PCF Überlagertes Eigengewicht (auf dem Boden): 100 psf Überlagertes Eigengewicht (auf Dach): 50 psf |
Abbildung 1. Standort (von Google Maps).
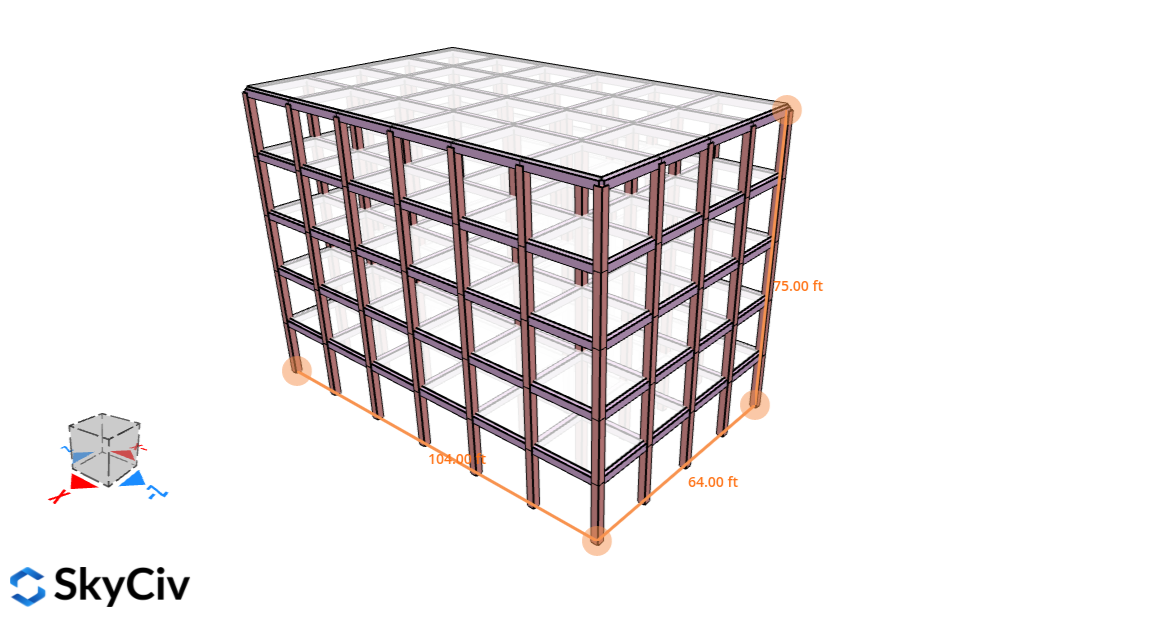
Abbildung 2. Struktur für dieses Beispiel.
USGS Seismische Daten
USGS hat eine Open-Source-Website seismische Daten die über ihre Design Web Services API verwendet werden können. Bei dieser Berechnung, Wir benötigen nur die folgenden Daten:
- \({S.}_{D1}\) ist der Design-Spektralantwort-Beschleunigungsparameter bei einer Periode von 1.0 s
- \({S.}_{1}\) ist das kartierte Maximum, das als Beschleunigungsparameter für die spektrale Reaktion auf Erdbeben betrachtet wird
- \({S.}_{DS}\)ist der Entwurfsparameter für die spektrale Reaktionsbeschleunigung im Kurzperiodenbereich
- \({T.}_{L.}\) ist die lang andauernde Übergangszeit
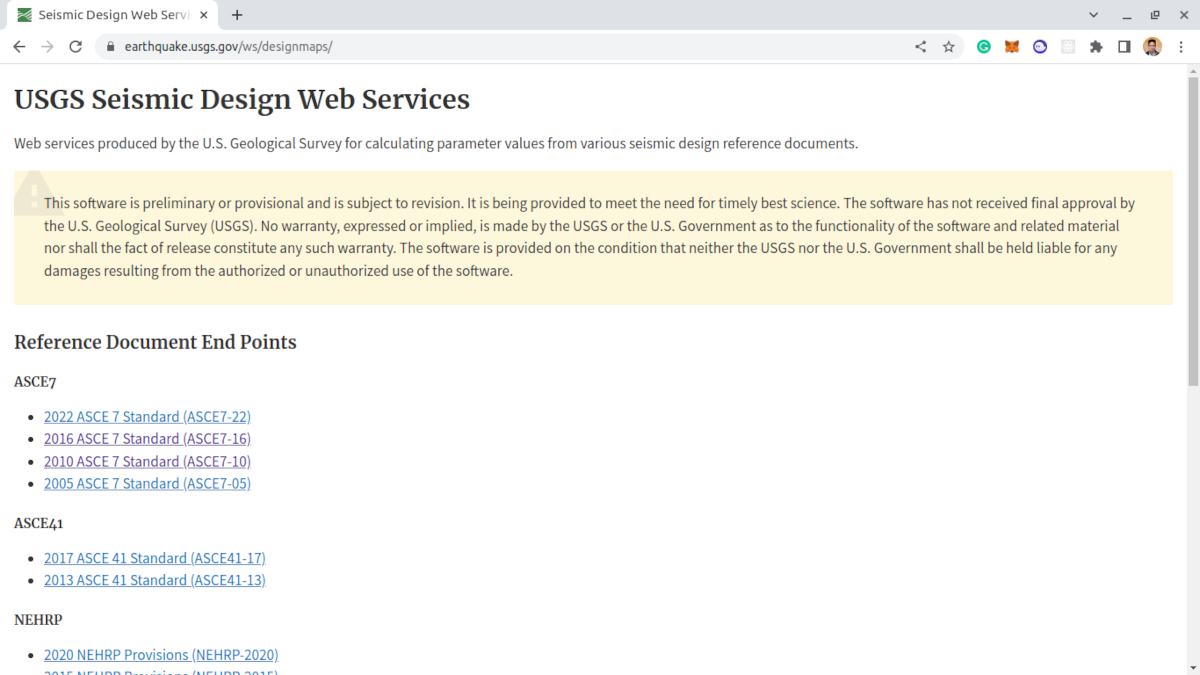
Abbildung 3. USGS Seismic Design-Webdienste.
Um die oben genannten Daten anzufordern, benötigen wir die folgenden Daten:
- Breite, Längengrad, den wir von Google Maps erhalten können
- Risikokategorie der Struktur basierend auf Abschnitt 1.5 von ASCE 7-16
- Standortklasse basierend auf Tabelle 20.3-1 von ASCE 7-16
Äquivalentes Querkraftverfahren
Die Erdbebenbemessungsbasisscherung kann mit Gleichung berechnet werden 12.8-1 von ASCE 7-16:
\( V = {C.}_{S.} W. \) (Gl. 12.8-1)
Wo:
\( V \) ist die Grundscherung für die seismische Bemessung
\( {C.}_{s} \) ist der seismische Reaktionskoeffizient basierend auf Abschnitt 12.8.1.1
\( W. \) ist das effektive seismische Gewicht gemäß Abschnitt 12.7.2
Die Formel zur Bestimmung des seismischen Antwortkoeffizienten lautet:
\( {C.}_{s} = frac{{S.}_{DS}}{ \frac { R. }{ {I}_{e} } } \) (Gl. 12.8-2)
Wo:
\( {S.}_{DS} \) ist der Entwurfsparameter für die spektrale Reaktionsbeschleunigung im Kurzperiodenbereich (von USGS-Daten)
\( R. \) ist der Response-Modifikationsfaktor gemäß Tabelle 12.2-1
\( {I}_{e} \) ist der aus Abschnitt ermittelte Wichtigkeitsfaktor 11.5.1
Jedoch, wir müssen Gleichungen erfüllen 12.8-3 zu 12.8-6:
Der Wert von \({C.}_{s}\) sollte nicht überschritten werden 12.8-3 oder 12.8-4
Zum \( T ≤ {T.}_{L.}\):
\({C.}_{s,max} = frac { {S.}_{D1}}{ \frac{TR}{{I}_{e}}} \) (Gl. 12.8-3)
Zum \( T. > {T.}_{L.}\) :
\({C.}_{s,max} = frac { {S.}_{D1} {T.}_{L.} }{ \frac{ {T.}^{2} R.}{{I}_{e}}} \) (Gl. 12.8-4)
Außerdem, \( {C.}_{s} \) darf nicht kleiner als Gleichung sein 12.8-5
\( {C.}_{s,Mindest} = 0.044 {S.}_{DS} {I}_{e} ≥ 0.01 \) (Gl. 12.8-5)
Zusätzlich, für Strukturen, die sich wo befinden \( {S.}_{1} ≥ 0,6 g):
\( {C.}_{s,Mindest} = 0.5 \frac {{S.}_{1}} { \frac{R.}{{I}_{e}}} \) (Gl. 12.8-6)
Wo
\( {S.}_{D1} \) ist der Beschleunigungsparameter für die spektrale Antwort des Entwurfs im Zeitraum von 1.0 s (von USGS-Daten)
\( T. \) ist die grundlegende Periode der Struktur
\( {T.}_{L.} \) ist die lange Übergangszeit (von USGS-Daten)
\( {S.}_{1} \) ist der kartierte maximal berücksichtigte Erdbeben-Spektralreaktionsbeschleunigungsparameter (von USGS-Daten)
Sobald wir den Wert der seismischen Bemessungsbasisscherung berechnet haben \( V \), Wir müssen die Kräfte mithilfe von Abschnitt entlang der Höhe der Struktur verteilen 12.8.3 von ASCE 7-16. In diesem Beispiel, Wir gehen davon aus, dass die Struktur keine vertikalen oder horizontalen Unregelmäßigkeiten aufweist.
\( {F.}_{x} ={C.}_{vx} V \) (Gl. 12.8-11)
\( {C.}_{vx} = frac {{w}_{x}{{h}_{x}}^{k}} { \Summe_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}^n{w}_{ich}{{h}_{ich}}^{k}} \) (Gl. 12.8-12)
Wo
\( {C.}_{vx} \) ist der vertikale Verteilungsfaktor
\( {w}_{ich} \) und \( {w}_{x} \) ist der Anteil am gesamten effektiven seismischen Gewicht der Struktur \( W. \) befindet oder einer Ebene zugeordnet ist ich oder x
\( {h}_{ich} \) und \( {h}_{x} \) ist die Höhe von der Basis bis zum Niveau ich oder x
\( k \) ist wie folgt definiert:
- \( k = 1 \) für Strukturen mit \( T ≤ 0.5 s)
- \( k = 2 \) für Strukturen mit \( T ≥ 2.5 s)
- lineare Interpolation von \( k \) für \( 0.5 < T. < 2.5 s \)
Zusätzlich, Boden- und Dachscheibenkräfte können mit Abschnitt ermittelt werden 12.10.1 von ASCE 7-16. Die Bemessungskraft kann mithilfe von Gleichungen berechnet werden 12.10-1 zu 12.10-3:
\( {F.}_{px} = frac { \Summe_{ich=x}^n {F.}_{ich}} { \Summe_{ich=x}^n {w}_{ich} }{w}_{px} \) (Gl. 12.10-1)
\( {F.}_{px,Mindest} = 0.2 {S.}_{DS}{I}_{e}{w}_{px} \) (Gl. 12.10-2)
\( {F.}_{px,max} = 0.4 {S.}_{DS}{I}_{e}{w}_{px} \) (Gl. 12.10-3)
Wo
\( {F.}_{px} \) ist die Auslegungskraft der Membran in der Ebene x
\( {F.}_{ich} \) ist die auf der Ebene aufgebrachte Bemessungskraft ich
\( {w}_{ich} \) ist das Gewicht, das dem Niveau zufließt ich
\( {w}_{px} \) ist das Gewicht, das dem Zwerchfell auf Höhe zufließt x
Wir werden weiter unten tiefer in diese Parameter eintauchen und das Konzept auf unsere Struktur anwenden.
Wichtigkeitsfaktor, \( {I}_{e} \)
Der Wichtigkeitsfaktor, \( {I}_{e} \), für die Struktur kann aus Abschnitt bestimmt werden 11.5.1 was auf Tabelle zeigt 1.5-2 von ASCE 7-16.
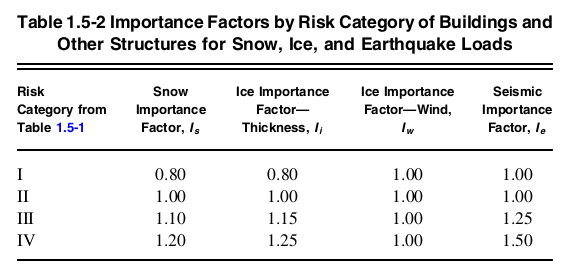
Abbildung 4. Tabelle 1.5-2 von ASCE 7-16 Angabe der Wichtigkeitsfaktorwerte pro Risikokategorie.
Da fällt der Aufbau unter Risikokategorie II, der entsprechende Wichtigkeitsfaktor \( ICH_{e} \) entspricht 1.0 basierend auf Tabelle 1.5-2.
\( {I}_{e} = 1.0 \)
Reaktionsmodifikationsfaktor, \( R. \)
Der Antwortmodifikationsfaktor, \( R. \), können aus der Tabelle ermittelt werden 12.2-1 je nach verwendetem Struktursystem. In diesem Beispiel, wir gehen davon aus, dass das verwendete Struktursystem ist “Spezielle Stahlbeton-Momentrahmen” für X- und Z-Richtung. Davon, wir können diesen Wert bestimmen \( R. \) entspricht 8 gemäß Tabelle 12.2-1.
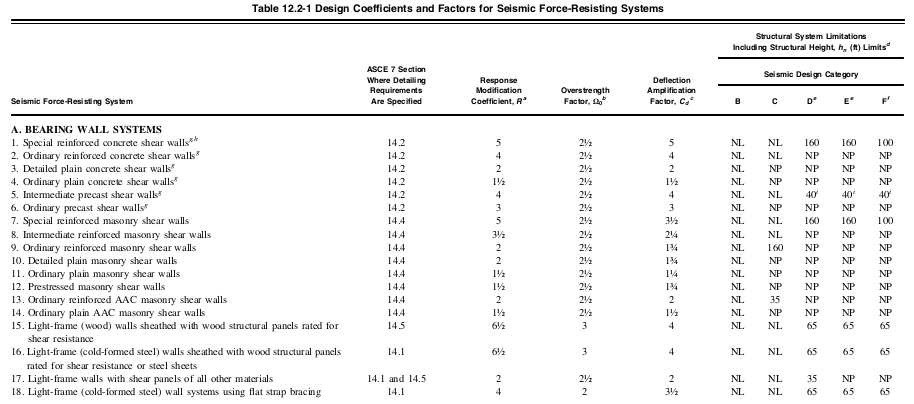
Abbildung 5. Abgeschnittene Werte der Tabelle 12.2-1 von ASCE 7-16 Angabe des Response Modification Coefficient, \( R. \), pro Struktursystem.
Site-Klasse
Für unsere seismische Belastung zu berechnen, Der Standort, den wir verwenden werden, ist bei Raleigh Hills, Portland, ODER, USA basierend auf Erdbebenlasten: Leitfaden zu den Bestimmungen für seismische Lasten von ASCE 7-16 (Charneyet al., 2020) welches klassifiziert ist als Standortklasse C.
USGS Seismische Daten
.Die seismischen USGS-Daten für den Standort lauten wie folgt:
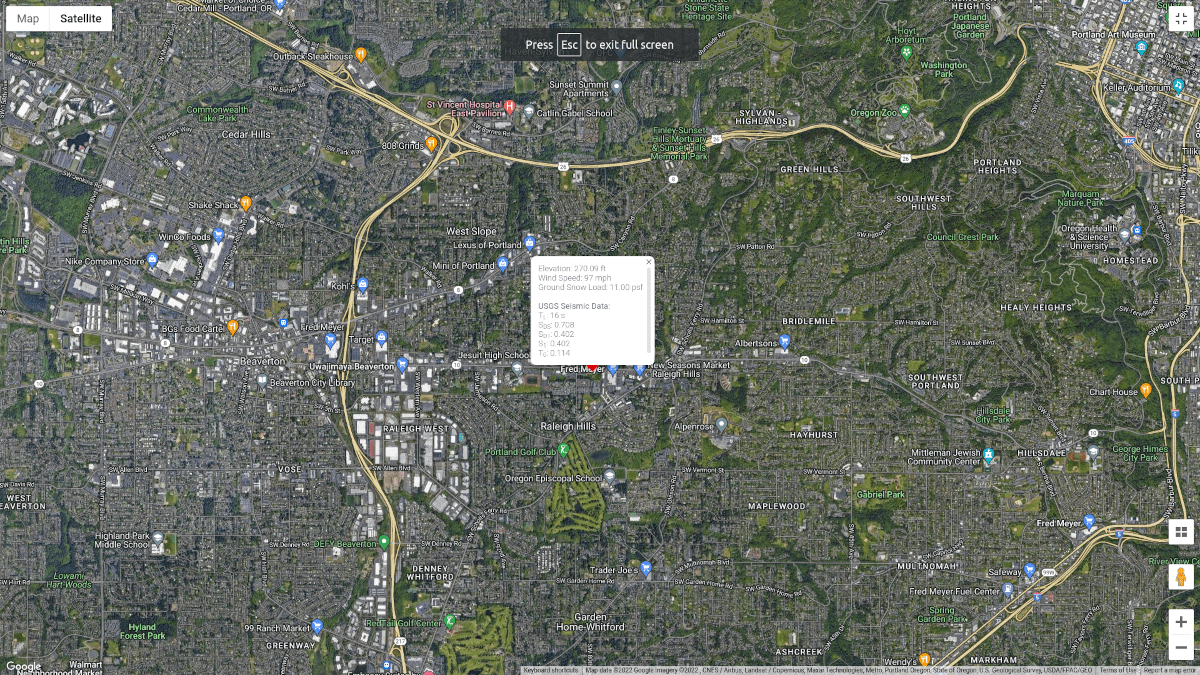
SkyCiv hat jetzt die seismischen Daten der Website von der USGS-Web-API integriert. Probier unser SkyCiv Lastgenerator!
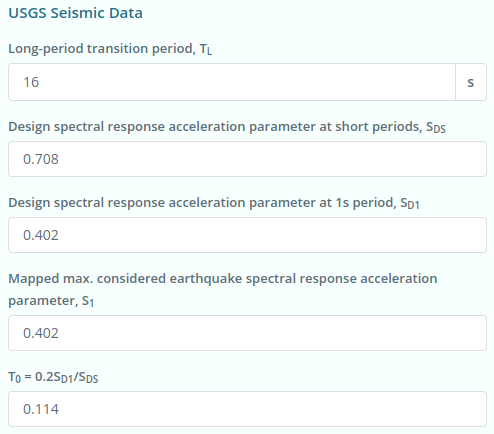
Abbildung 6. Seismische Standortdaten von USGS Web Services.
\({S.}_{D1} = 0.402 \)
\({S.}_{1} = 0.402 \)
\({S.}_{DS} = 0.708 \)
\({T.}_{L.} = 16 s \)
\({T.}_{0} = 0.114 \)
Kategorie seismisches Design
Sektion 11.6 von ASCE 7-16 beschreibt das Verfahren zur Bestimmung der seismischen Entwurfskategorie der Struktur basierend auf der Risikokategorie und der Standortklasse für die Struktur.
- Zum \({S.}_{1} ≥ 0.75 \) und Risikoklasse I, II, oderIII, die Erdbebendesign-Kategorie wird der Erdbebendesign-Kategorie E zugeordnet
- Zum \({S.}_{1} ≥ 0.75 \) und Risikokategorie IV, die Erdbebendesign-Kategorie wird der Erdbebendesign-Kategorie F zugeordnet
- Andernfalls, Tabelle 11.6-1 und Tabelle 11.6-2 verwendet werden, was schwerer ist.
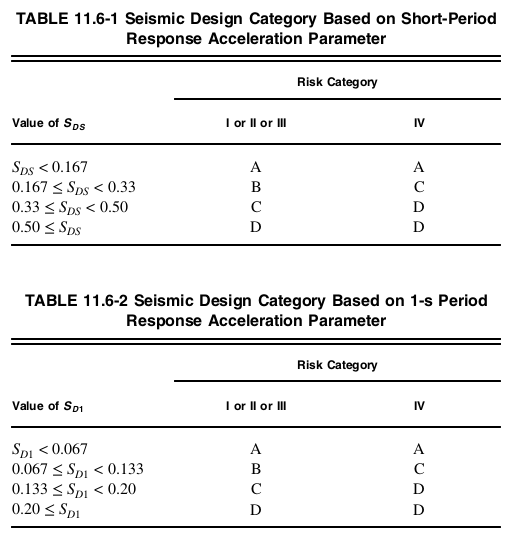
Abbildung 7. Kategorie seismische Bemessung aus Abschnitt 11.6 von ASCE 7-16.
Für diese Struktur, mit Risikoklasse II, \({S.}_{D1} = 0.402 \), und \({S.}_{DS} = 0.708 \) die seismische Entwurfskategorie ist D, basierend auf beiden Tabellen 11.6-1 und 11.6-2 von ASCE 7-16. Die seismische Entwurfskategorie wird für den Redundanzfaktor verwendet \( r \) bei der Berechnung der Konstruktionskräfte der Membran.
Fundamentale Periode der Struktur \( T. \)
Die Grundperiode einer Struktur kann aus der Modalanalyse der Struktur bestimmt werden. ASCE 7-16 ermöglicht die Annäherung der Grundperiode einer Struktur mit Section 12.8.2.1.
\( {T.}_{ein} = {C.}_{t} {{h}_{n}}^{x} \)
Wo \( {h}_{n} \) ist die Bauhöhe des Bauwerks (vertikaler Abstand von der Basis bis zur höchsten Ebene des erdbebensicheren Systems des Bauwerks), und \( {C.}_{t} \) und \( x \) können aus der Tabelle ermittelt werden 12.8-2.
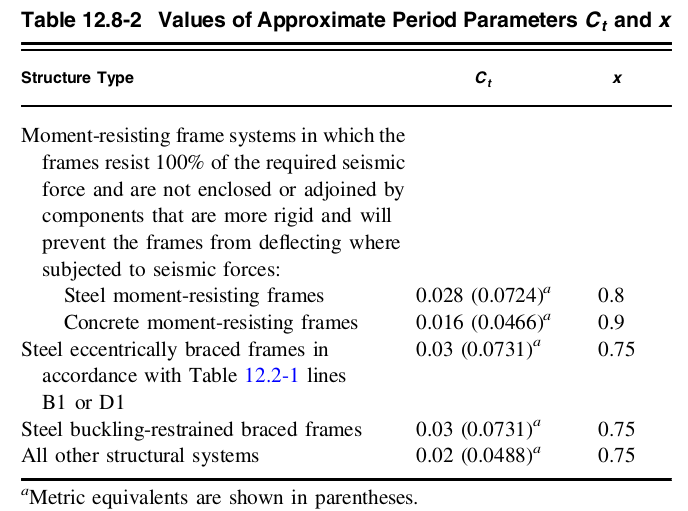
Abbildung 8. Werte von \( {C.}_{t} \) und \( x \) aus der Tabelle 12.8-2 von ASCE 7-16.
Da es sich bei der Struktur um einen Momententragrahmen aus Beton handelt:
\( {C.}_{t} = 0.016\)
\( x = 0.9\)
Deshalb, Strukturhöhe verwenden \( {h}_{n} \) gleich 75 ft., die ungefähre Grundperiode der Struktur \( {T.}_{ein} \) bestimmt werden kann:
\( {T.}_{ein} = {C.}_{t} {{h}_{n}}^{x} = (0.016) {(75)}^{0.9}\)
\( T = {T.}_{ein} = 0.7792 s)
Seismischer Reaktionskoeffizient \({C.}_{s}\)
Aus den obigen Werten, wir können bereits den seismischen Reaktionskoeffizienten berechnen \({C.}_{s}\):
\( {C.}_{s} = frac{ {S.}_{DS} }{ \frac {R.}{{I}_{e}} } = frac{ 0.402 }{ \frac {8}{1.0} } \)
\( {C.}_{s} = 0.0885\)
Schon seit \( T ≤ {T.}_{L.}\):
\({C.}_{s,max} = frac { {S.}_{D1}}{ \frac{TR}{{I}_{e}}} = frac { (0.402)}{ \frac{(0.7792)(8)}{(1.0)}} \)
\({C.}_{s,max} = 0.0645 \)
Zusätzlich, der Mindestwert von \( {C.}_{s} \) soll nicht kleiner sein als:
\( {C.}_{s,Mindest} = 0.044 {S.}_{DS} {I}_{e} ≥ 0.01 \)
\( {C.}_{s,Mindest} = 0.044 (0.402) (1.0) ≥ 0.01 \)
\( {C.}_{s,Mindest} = 0.0312 \)
Der Endwert von \( {C.}_{s} \) zur Berechnung herangezogen werden:
\( {C.}_{s} = 0.0645\)
Effektives seismisches Gewicht \( W. \)
In diesem Beispiel, Wir berechnen das effektive seismische Gewicht unter Verwendung der Eigen- und Auflast, die auf die Böden aufgebracht werden. Außen- und Innenwände werden gleich in die aufgelagerte Bodeneigenlast einfließend angenommen 100 psf. Mit konkretem Einheitsgewicht gleich 156 lb/cu.ft.:
Für typische Bodenhöhe (ausgenommen Boden- und Dachebenen):
Spalte: Typische Geschosshöhe x Querschnittsfläche x Gewicht der Betoneinheit x Gesamtzahl. Spalten = 15 ft x 156 lb/cu.ft. x (20″x20″) x 35 = 227.5 Kips
Platte: Bodenfläche x Dicke x Gewicht der Betoneinheit = 64ft (104 ft) x 8″ x 156 lb/cu.ft. = 692.224 Kips
Balken: Gesamtlänge x Querschnittsfläche x Einheitsgewicht des Betons = 968 ft x 156 lb/cu.ft. x (14″x20″) = 293.627 Kips
Überlagertes Eigengewicht: Bodenfläche x Last = 64ft (104 ft) x 100 psf= 665.6 Kips
Gesamte Totlast pro Ebene: 1878.951 Kips
Für Dachebene:
Spalte: Typische Geschosshöhe x Querschnittsfläche x Gewicht der Betoneinheit x Gesamtzahl. Spalten = 7.5 ft x 156 lb/cu.ft. x (20″x20″) x 35 = 113.75 Kips
Platte: Bodenfläche x Dicke x Gewicht der Betoneinheit = 64ft (104 ft) x 8″ x 156 lb/cu.ft. = 692.224 Kips
Balken: Gesamtlänge x Querschnittsfläche x Einheitsgewicht des Betons = 968 ft x 156 lb/cu.ft. x (14″x20″) = 293.627 Kips
Überlagertes Eigengewicht: Bodenfläche x Last = 64ft (104 ft) x 50 psf= 332.8 Kips
Gesamte Eigenlast auf Dachebene: 1432.401 Kips
Zusammenfassend:
| Erdgeschoss | Elevation, ft | Gewicht, wx, Kips |
| Dach | 75 | 1432.401 |
| 5Stufe | 60 | 1878.951 |
| 4Stufe | 45 | 1878.951 |
| 3rd-Ebene | 30 | 1878.951 |
| 2Stufe | 15 | 1878.951 |
| Effektives seismisches Gewicht, W. | 8948.203 | |
\( W = 8949.203 [object Window])
Seismische Basisscherung \( V \)
Gleichung verwenden 12.8-1 von ASCE 7-16, die seismische Basisscherung kann berechnet werden:
\( V = {C.}_{S.} W = (0.0645)(8948.203) \)
\( V = 577.159 Kips \)
Vertikale Verteilung seismischer Kräfte \( {F.}_{x} \)
Wir müssen die seismische Belastung über die gesamte Struktur verteilen. Da die grundlegende Periode der Struktur ist \( T = {T.}_{ein} = 0.7792 s), deshalb:
\( k = 1.1396\)
Um die seismische Kraft zu berechnen \( {F.}_{x} \) pro Ebene, Der beste Ansatz besteht darin, die seismischen Gewichte pro Ebene tabellarisch aufzulisten:
| Erdgeschoss | \( {w}_{x} \) Kips | \( {h}_{x} \) ft | \( {w}_{x} {{h}_{x}}^{k} \) | \( {C.}_{vx} \) |
\( {F.}_{x} \) Kips |
| Dach | 1432.401 | 75 | 196303.644 | 0.2923 | 168.6950 |
| 5Stufe | 1878.951 | 60 | 199681.715 | 0.2973 | 171.5980 |
| 4Stufe | 1878.951 | 45 | 143865.010 | 0.2142 | 123.6315 |
| 3rd-Ebene | 1878.951 | 30 | 90631.141 | 0.1349 | 77.8845 |
| 2Stufe | 1878.951 | 15 | 41135.482 | 0.0612 | 35.3501 |
| S = 671616.992 | \( V \) = 577.1591 |
Membrankräfte \( {F.}_{px} \)
Die Berechnung der Membrankräfte ist unten dargestellt. Da wir davon ausgegangen sind, dass es keine Unregelmäßigkeiten gibt, der Redundanzfaktor \( r \) ist eingestellt auf 1.0. Dieser Parameter soll mit multipliziert werden \( {F.}_{px} \):
| Erdgeschoss | \( {w}_{px} \) Kips | \( Σ {w}_{ich} \) |
\( Σ {F.}_{ich} \) | \( {F.}_{px,Mindest} \) | \( {F.}_{px,max} \) | \( {F.}_{px} \) | Design \( {F.}_{px} \) |
| Dach | 1432.401 | 1432.401 | 168.6950 | 202.8279 | 405.6559 | 168.6950 | 202.8279 |
| 5Stufe | 1878.951 | 3311.351 | 340.2930 | 266.0594 | 532.1188 | 193.0915 | 266.0594 |
| 4Stufe | 1878.951 | 5190.302 | 463.9245 | 266.0594 | 532.1188 | 167.9461 | 266.0594 |
| 3rd-Ebene | 1878.951 | 7069.253 | 541.8090 | 266.0594 | 532.1188 | 144.0085 | 266.0594 |
| 2Stufe | 1878.951 | 8948.203 | 577.1591 | 266.0594 | 532.1188 | 121.1923 |
266.0594 |
SkyCiv Lastgenerator
Alle diese Berechnungen sind bereits im SkyCiv-Lastgenerator enthalten. Optimieren Sie Ihre Berechnung mit unserem kostenlosen Erdbebenlastrechner für ASCE 7-16!
Seismische Daten des Standorts
Die seismischen USGS-Daten können nach der Risikokategorie abgerufen werden, Site-Klasse, und Projektadresse sind definiert. Beachten Sie, dass die Parameter \({S.}_{D1} \), \({S.}_{1} \), \({S.}_{DS} \), und \({T.}_{L.} \) Werte haben sollten, um mit der seismischen Lastberechnung fortzufahren.
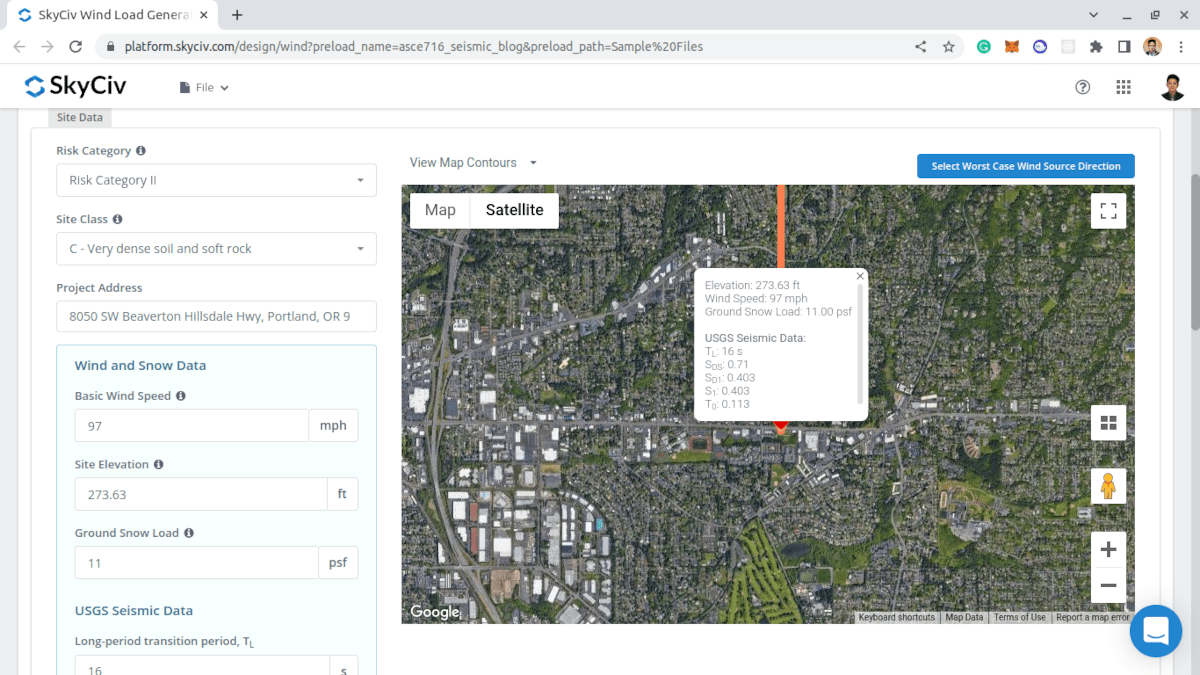Abbildung 9. Parameter, die zum Abrufen der seismischen USGS-Daten für den Standort erforderlich sind.
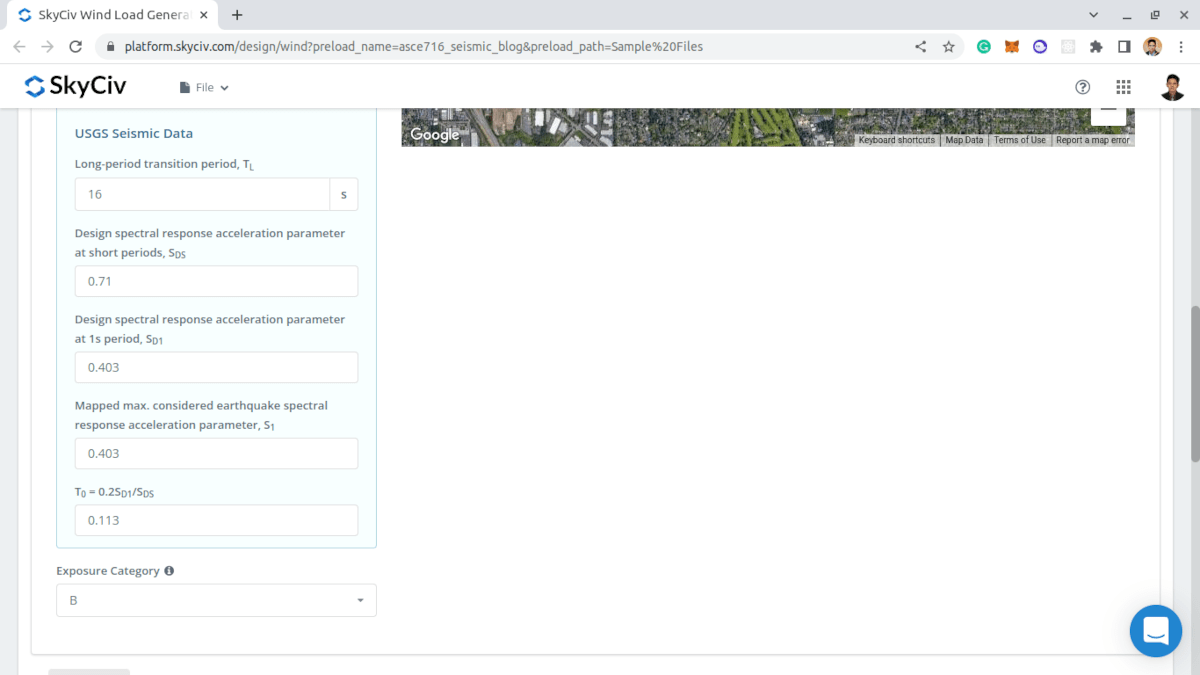
Abbildung 9. Ergebnisse aus seismischen USGS-Daten.
Benutzer können die von USGS Web Services erhaltenen Parameter ändern, um die am besten geeignete seismische Belastung für die Struktur zu erhalten.
Strukturdaten
Auf der Registerkarte Strukturdaten, Sie müssen lediglich die Standard-Gebäudedaten definieren: Dachprofil, Gebäudelänge, Gebäudebreite, Mittlere Dachhöhe, und Dachneigungswinkel.
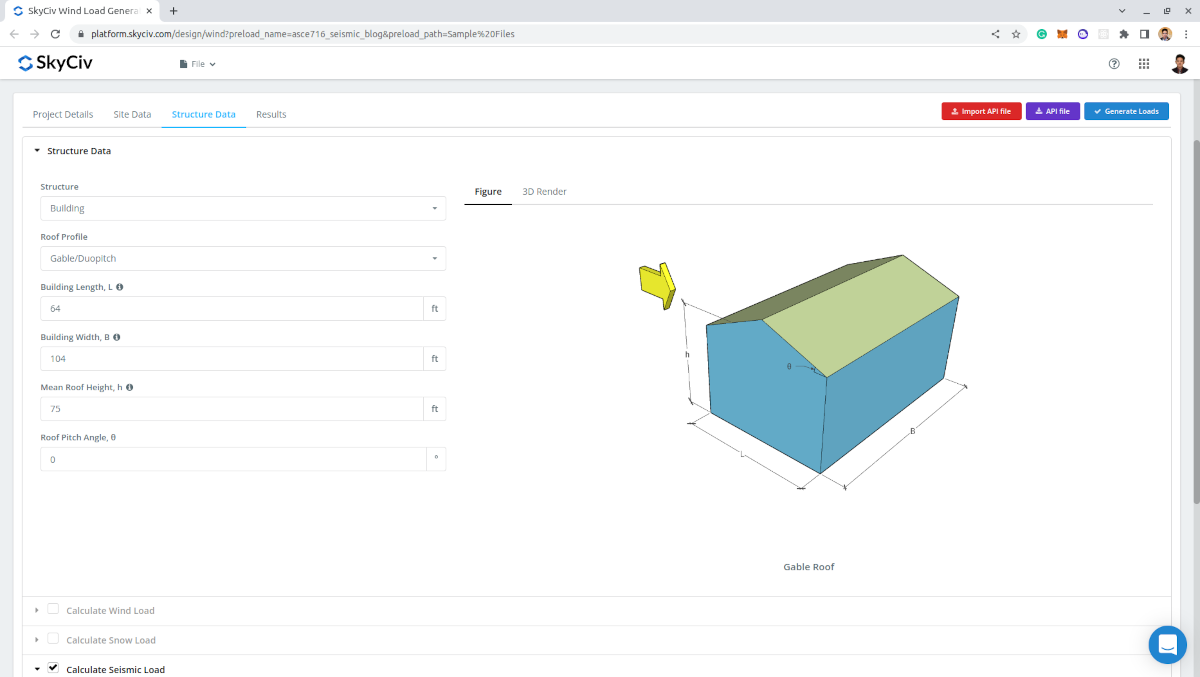
Abbildung 10. Gebäudedateneingabe.
Seismische Daten
Um mit den seismischen Berechnungen fortzufahren, die erforderlichen sind die folgenden:
- Struktursystem – zur Bestimmung der Werte von \({C.}_{t} \) und \(x \) die zur Berechnung der ungefähren Grundperiode der Struktur verwendet werden \({T.}_{ein} \)
- Ungefähre grundlegende Periode der Struktur \({T.}_{ein} \) – kann für eine angemessenere seismische Lastberechnung benutzerdefiniert werden
- Reaktionsmodifikationsfaktor \( R. \) – Standardwert ist 8.5 und für geeignetere seismische Ergebnisse modifiziert werden
- Redundanzfaktor, \( r \) – Standardwert ist 1.0 und kann geändert werden. Wird bei der Berechnung der Membrankräfte verwendet
- Bodengewichte – wird für die vertikale Verteilung des Basisschubs und für Membrankräfte verwendet. Daten pro Ebene erforderlich sind: Niveau (zur Benennung), Elevation, und Gewicht
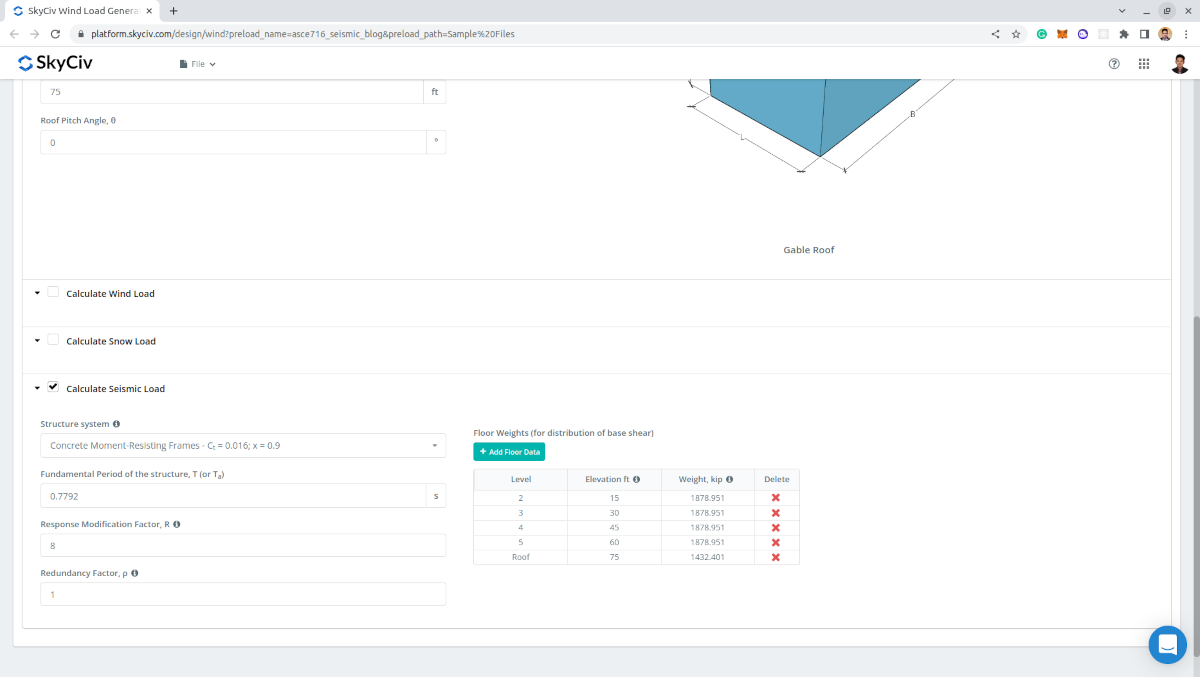
Abbildung 11. Seismische Parameter, die für die seismische Berechnung erforderlich sind.
Ergebnisse
Das Ergebnis der Berechnung sind die verwendeten seismischen Parameter und die berechnete seismische Basisscherung \(V \), seismische Kräfte pro Ebene, und Membrankräfte pro Ebene.
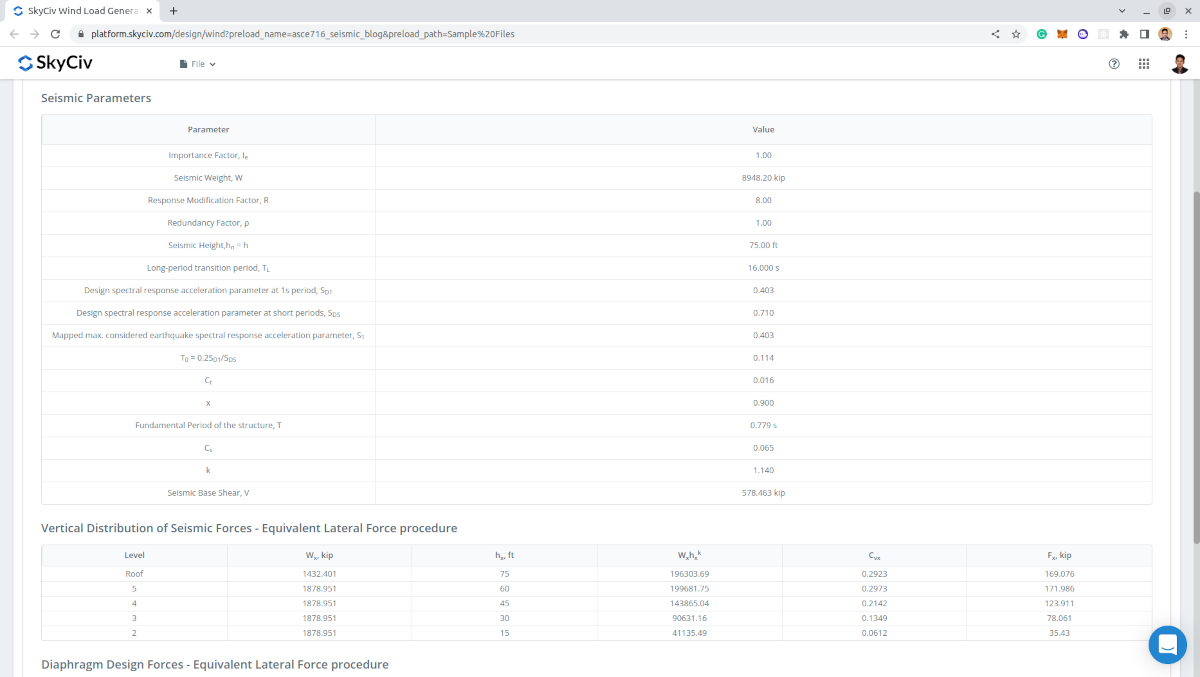
Abbildung 12. Eingabeparameter und Ergebnisse für die Erdbebenlastberechnung.
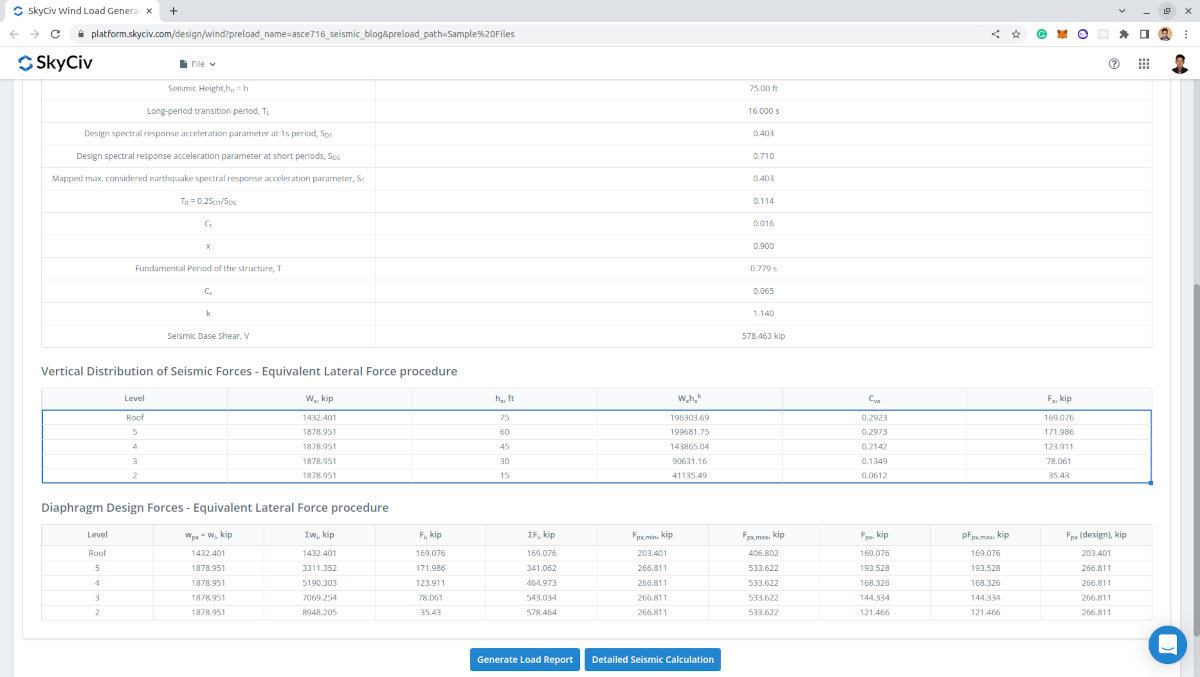
Abbildung 13. Tabellierte seismische Kräfte pro Ebene, einschließlich der Membranbemessungskräfte.
Ausführlicher Bericht
Beim Generieren der Ergebnisse, Professionelle Kontonutzer und diejenigen, die die gekauft haben Standalone-Lastgeneratormodul kann eine detaillierte seismische Berechnung erstellen. Der Bericht zeigt alle Parameter und Annahmen, die in der seismischen Berechnung verwendet wurden, um sie für den Benutzer transparent zu machen. Der generierte Bericht für diese Beispielrechnung kann hierüber aufgerufen werden link.
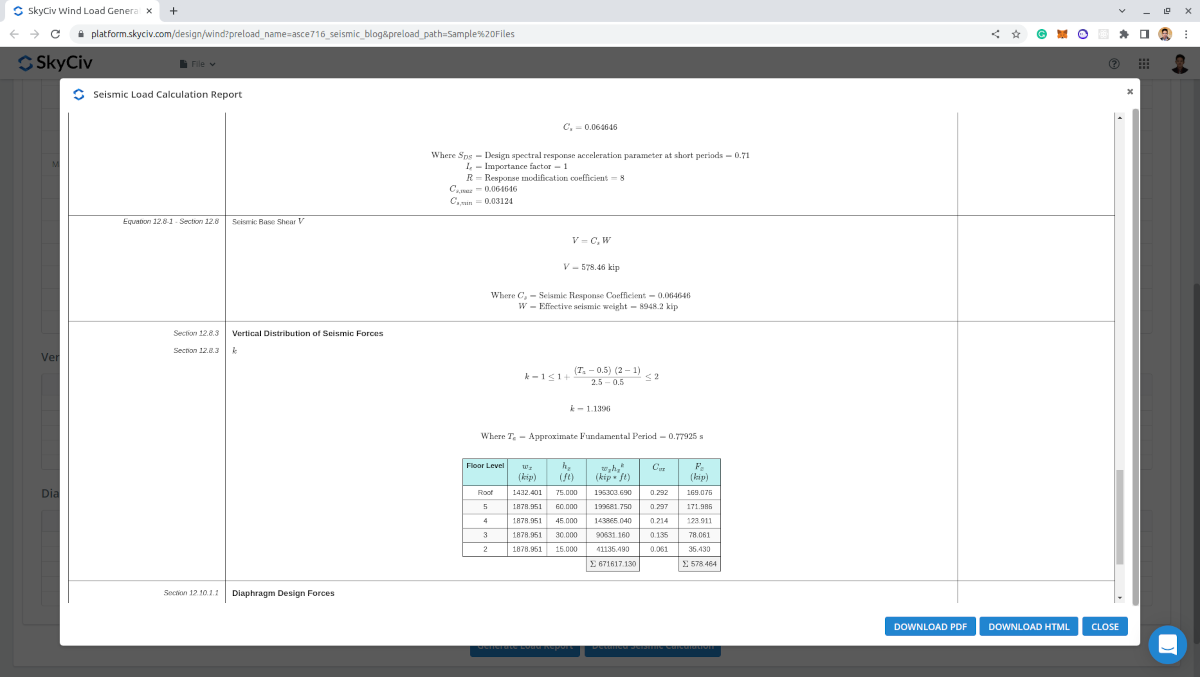
Abbildung 14. Detaillierte Berechnung der seismischen Last des SkyCiv-Lastgenerators.
Nutzen Sie diese Funktion, indem Sie Anmeldung für ein professionelles Konto oder durch den Kauf der Standalone-Lastgeneratormodul! Für bestehende Benutzer, ein KOSTENLOSE DEMO ist auch verfügbar, wenn Sie eine umfassendere Lösung für Lastberechnungen benötigen.
Für zusätzliche Ressourcen, Sie können diese Links verwenden:
Statiker, Produktentwicklung
MS Bauingenieurwesen
Verweise:
- Amerikanische Gesellschaft der Bauingenieure. (2017, Juni). Minimale Auslegungslasten und zugehörige Kriterien für Gebäude und andere Strukturen. Amerikanische Gesellschaft der Bauingenieure.
- Charney, F., Heusler, T., und Marshall, J.. (2020). Erdbebenlasten: Leitfaden zu den Bestimmungen für seismische Lasten der ASCE 7-16. Amerikanische Gesellschaft der Bauingenieure.
- Google Maps
