Berechnen Sie die Eigenfrequenzen Ihrer Struktur in Structural 3D
Dynamische Frequenzanalyse, oder Modalanalyse, wird benötigt, um die Eigenfrequenzen zu bestimmen (oder Resonanzfrequenzen) einer Struktur, um ihre maximale Antwort vorherzusagen. Wenn eine auf die Struktur ausgeübte Vibrationslast mit der Eigenfrequenz übereinstimmt, Dies kann gefährlich sein und zur Zerstörung des Systems führen.
Eingang
Benutzer können problemlos Knotenmassen hinzufügen, durch einfaches Umwandeln ihrer vorhandenen statischen Lasten in Knotenmassen. SkyCiv Structural 3D berechnet automatisch die Knotenmassen (basierend auf Ihren Lastgruppen) und wenden Sie sie auf die Struktur an, So kann Ihr Modell auf dynamische Frequenzeffekte analysiert werden. Anfangen, klicken Knotenmassen aus dem linken Menü. Benutzer können Knotenmassen aus vorhandenen Lasten konvertieren. Hier ist ein Beispiel dafür, wann ein Benutzer klickt Lasten konvertieren unter dem Knotenmassen Eingang:
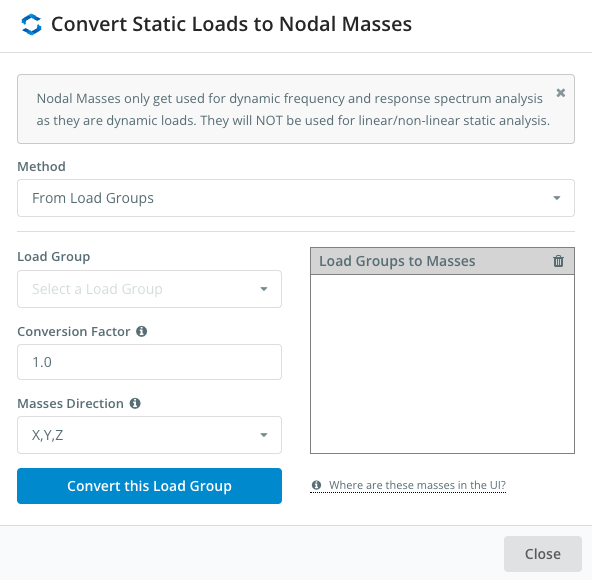
Auf diese Weise können Benutzer Lastgruppen hinzufügen und in modale Massen konvertieren, Geben Sie dem Benutzer die volle Kontrolle darüber, welche Lasten enthalten sind, mit Kontrollen für Massenrichtungen und Faktoren.
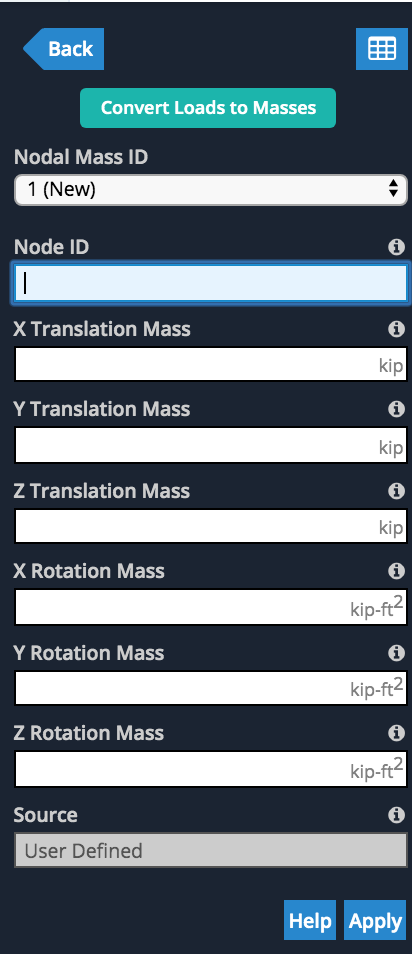
Benutzer können auch ihre eigenen Knotenmassen an jedem Knoten angeben, indem sie in das X eingeben,UND,Z Translations- und Rotationsmassenwerte:
Dynamische Frequenzanalyse
Die SkyCiv Dynamic Frequency-Analyse berechnet die niedrigsten Eigenfrequenzen der Struktur, durch Lösen der folgenden Eigenwertgleichung. In einer statischen Analyse, Wir gehen davon aus, dass das System nicht von der Zeit abhängt. In der dynamischen Analyse, Es besteht eine Zeitabhängigkeit.
Während der dynamischen Frequenzanalyse lösen wir die Modenformen und -frequenzen unter Vibration. Insbesondere lösen wir die Schwingungsfrequenz (Zyklen pro Sekunde) und Punkt (die Zeit, die benötigt wird, um einen Zyklus abzuschließen) für jede Modenform der Struktur.
Die folgende Formel stellt die Berechnungen dar, die von Structural 3D während einer Frequenzanalyse durchgeführt wurden:
[M.][U.¨]+[K.][U.]=[0]
[M.] = Strukturmassenmatrix,
[K.] = Struktursteifigkeitsmatrix,
[U.] = Verschiebung,
[U.¨] ist die doppelte Ableitung der Verschiebung in Bezug auf die Zeit (d.h.. Beschleunigung).
Hier, Die Gleichung ist nicht gelöst, sondern es wird auf ein allgemeines Eigenwertproblem reduziert. Wo λ = Eigenwerte
[M.][U.]λ+[K.][U.]=[0]
Die resultierenden Eigenwerte sind die Frequenzen der Struktur, während die Eigenvektoren die Modusformen sind. Eine niedrigere Frequenz oder ein niedrigerer Modus bedeutet weniger Zyklen pro Sekunde und damit eine langsamere Schwingung.
Ergebnisanzeige
Sobald die dynamische Frequenzanalyse abgeschlossen ist, Benutzer können die Ergebnisse mehrerer Modusformen überprüfen. Wählen Sie einfach die Modusform, und die Struktur wird animiert, um die Modenform anzuzeigen. Benutzer können auch die Frequenz- und Periodenwerte für alle Modi der Struktur überprüfen. Hier ist ein Beispiel für die Animation und die Ergebnisse:
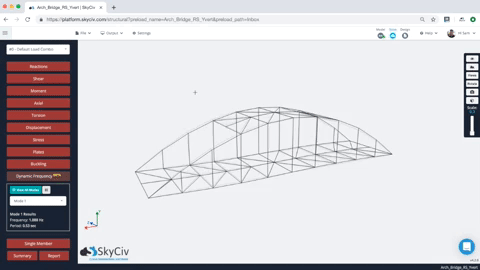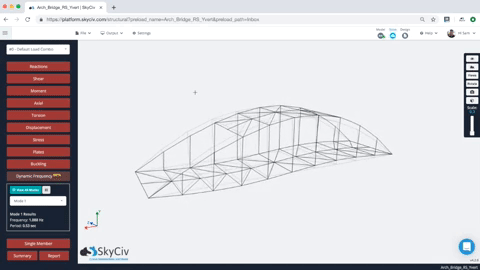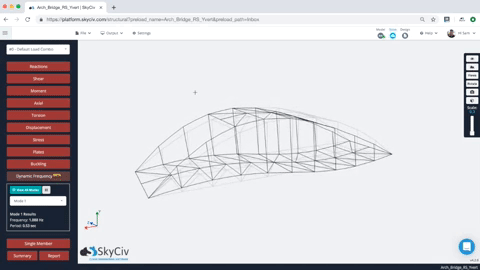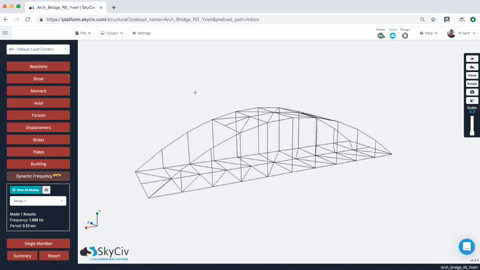
Benutzer erhalten außerdem eine tabellarische Ergebnisliste für jeden Modus, einschließlich der Eigenfrequenz und Periode. So zum Beispiel, Im obigen Modell haben wir die Häufigkeit und Periode jedes Ergebnisses (Hinweis zur Vereinfachung, nur der erste 10 Modi wurden generiert – Dies kann unter gesteuert werden die Einstellungen):
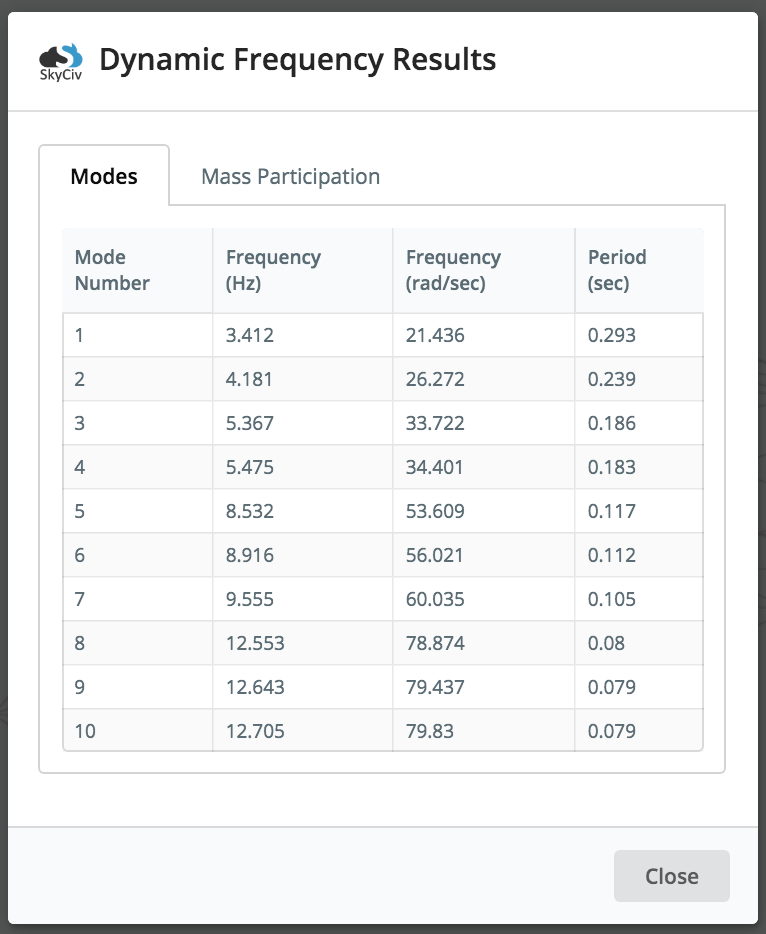
zusätzlich, Die modale Massenbeteiligung ergibt sich aus einer Struktur, und seine Modi können durch Klicken auf überprüft werden Massenbeteiligung Tab. Der Massenbeteiligungsfaktor gibt die Menge an Masse an, die mit der spezifischen Frequenz oder dem Schwingungsmodus verbunden ist. Es ermöglicht dem Benutzer im Wesentlichen zu sehen, wie viel von der Masse der Struktur mit dem gegebenen Modus angeregt wird. Dadurch erhalten Sie Einblicke in die Reaktion der Struktur: Je größer der Massenbeteiligungsfaktor, Je größer die Bedeutung für die Gesamtreaktion ist.
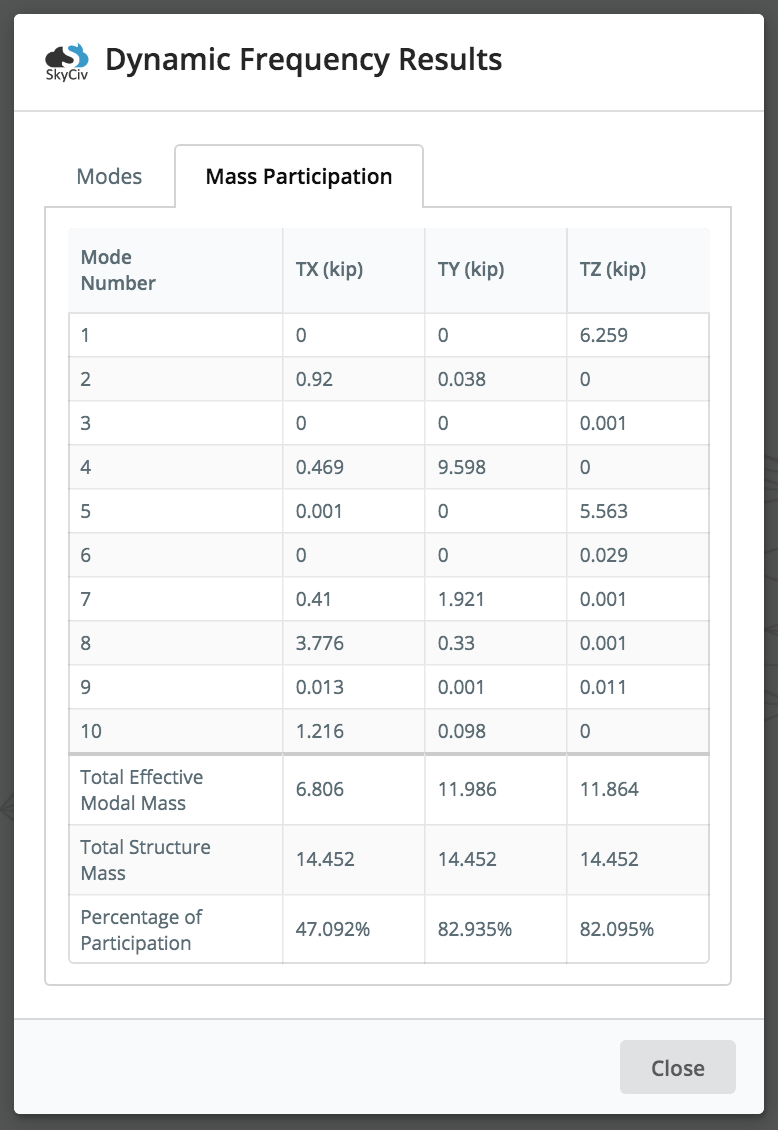
In der obigen Beispielanimation (die Brückenstruktur), Sie können sehen, dass sich die Brücke NUR in x- und y-Richtung für diesen Modus bewegt / vibriert (Modus 2), also davon, , 0 Beteiligungsfaktoren in z-Richtung (seitwärts). Beim Umgang mit relativ kleinen Massenbeteiligungsfaktoren, Der Benutzer sollte immer ein technisches Urteilsvermögen üben und die Auswirkungen dieser Schwingungsarten analysieren. Die meisten Bauvorschriften erfordern mindestens 90% kumulative Massenbeteiligung zur Analyse.
