In diesem Artikel, Wir werden ein Slab-Design-Beispiel unter Verwendung der letzten Version von ACI-318-19 entwickeln: “Bauvorschriften für Konstruktionsbeton,” bestehend aus der Modellierung eines Flachbaus aus Stahlbeton in SkyCiv, wobei der Schwerpunkt auf dem Vergleich von Softwareergebnissen und Handberechnungen anhand einer von ACI akzeptierten Methode liegt: “Das direkte Bemessungsverfahren für Decken.” Dieses Verfahren besteht darin, das Gesamtmoment anhand geeigneter Faktoren auf verschiedene Streifen entlang der Hauptrichtungen und Rahmen des Gebäudes aufzuteilen, um die Menge der Bewehrung und die Position in der Platte zu bestimmen.

Wir hoffen, dass Sie den vorherigen Artikel gelesen haben, Plattendesign in S3D, um sich mit dem Modellieren und Entwerfen von Platten mit SkyCiv vertraut zu machen. Eine weitere hilfreiche Information, die Sie unbedingt berücksichtigen sollten, finden Sie in So modellieren Sie Platten? Sobald Sie beide Dokumente vollständig gelesen haben, Fühlen Sie sich frei, in das folgende vollständige Beispiel für den Plattenvergleich einzutauchen!

Allgemeiner Gebäudeplan

Die folgenden Bilder zeigen eine isometrische Ansicht und Planmaße des zu berechnenden Beispiels. Das Gebäude hat zwei aufgeständerte Flachdecken ohne Unterzüge zwischen den Stützenstützen.

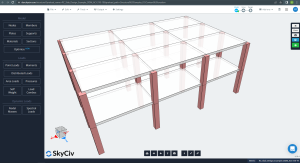
Abbildung 1. Isometrische Ansicht des Gebäudebeispiels

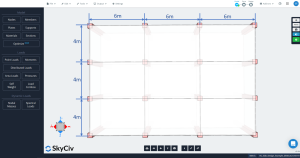
Abbildung 2. Abmessungen des Plattenplans

Direktes Bemessungsverfahren für Zwei-Weg-Platten (DDM)

Einschränkungen

ACI 318 ermöglicht die Verwendung des DDM zur Bemessung von Stahlbetonplatten für Schwerkraftlasten, die einige Requisiten nach Geometrie sammeln, Belastungsbeziehungen, Symmetrie, etc. Wir können diese Einschränkungen in der folgenden Liste zusammenfassen (PCA-Notizen):

• “In jeder Richtung müssen drei oder mehr durchgehende Spannweiten vorhanden sein.”: Abbildung 2 zeigt drei Spannweiten in jeder Hauptrichtung, längs und quer. OK!
• “Deckenplatten müssen rechteckig sein mit einem Verhältnis von längerer zu kürzerer Spannweite (Mittellinie zu Mittellinie der Stützen) nicht größer als 2.”: Laut Abbildung 2, das Verhältnis ist gleich \({\frac{l_1}{4}= frac{6m}{4m}=1,5 < 2}\). OK!
• “Aufeinanderfolgende Spannweiten (Mittellinie zu Mittellinie der Stützen) in jeder Richtung darf sich um nicht mehr als unterscheiden 1/3 der längeren Spanne”. Die Spannweiten sind in jede Richtung gleich, 6m in Längsrichtung und 4 m in Querrichtung. OK!
• “Spalten dürfen nicht mehr als versetzt werden 10% der Spannweite (in Versatzrichtung) von jeder Achse zwischen den Mittellinien aufeinanderfolgender Spalten”. Das Gebäudebeispiel weist keine Versätze in den Spalten auf. OK!
• “Lasten müssen gleichmäßig verteilt werden, bei der unfaktorisierten oder betriebsbedingten Verkehrslast nicht mehr als das Zweifache der unfaktorisierten oder betriebsbedingten Eigenlast (L/D ≤ 2)”. Nehmen Sie die Werte jeder Schwerkraftlast, Das Verhältnis ist definiert als \({\frac{L.}{D.}= frac{2}{7.8}=0,256 < 2}\). OK!.
• “Für zweiseitig trägergestützte Decken, Die relative Steifigkeit von Trägern in zwei senkrecht zueinander stehenden Richtungen muss die Mindest- und Höchstanforderungen der Norm erfüllen.” Schon zufrieden; Es gibt keine Balken in den Platten. OK!
• “Die Umverteilung negativer Momente per Code ist nicht gestattet.” Aufgrund der Einfachheit des Beispiels, Es ist nicht erforderlich, negative Momente in den Platten neu zu verteilen. OK!.

Definition der Längs- und Querstreifen

Die Platte in DDM muss für die Analyse und Bemessung eines bestimmten Linienrasters in zwei Hauptstreifen unterteilt werden: Säulen- und Mittelstreifen. Die Breite für Stützenstreifen ist die kleinere \({\frac {l_1}{4}}\) sowie \({\frac{l_2}{4}}\), wo \({l_1}\) ist die Länge der Spanne entlang des Liniengitters und \({l_2}\) ist die Querlänge senkrecht.

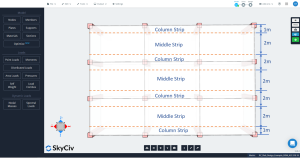
Abbildung 3. Längssäule und Mittelstreifen.

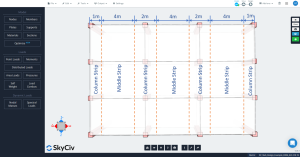
Abbildung 4. Quersäule und Mittelstreifen.

Minimale Dicke

ACI-318 schlägt die Verwendung der Gleichung vor: \({t_{Mindest}}= {\frac{l_n}{30}}={\frac{6m-0.50m}{30}}=0,1833m = 0,20m)

Vorläufige Prüfung der Scherfestigkeit

Vor der Berechnung der Stahlbewehrung, Es wird empfohlen, die Scherfestigkeit der Platte zu überprüfen, eine für den direkten Schub in der Verbindung und die andere für die Durchstanztragfähigkeit an der Verbindungsplattenstütze.

Berechnung des Scherbedarfs, Wir verwenden die folgenden Schwerkraftlasten:

• Eigengewichtsplatte: \({SW={\gamma_c}\mal {t_{Platte}}={24 {\frac{kN}{m^3}}}\mal {0.20m}=4,8{\frac{kN}{m^2}} }\)
• Überlagertes Eigengewicht: \({SD={3 {\frac{kN}{m^2}}}}\)
• Gesamte Eigenlast (SW+SD): \({D={7.8 {\frac{kN}{m^2}}}}\)
• Live-Last (Wohnbelegung) : \({L={2 {\frac{kN}{m^2}}}}\)
• Faktorisierte Kraftbelastung (1.2D+1,6L): \({q_{u}={12.56 {\frac{kN}{m^2}}}}\)

Der erste Schernachweis ist der “Balkenscherung” Art, wobei das folgende Bild den Bereich angibt, der zur Ermittlung der Gesamtscherung berücksichtigt werden muss. Wir prüfen jede Richtung, den größeren Bereich einnehmen.

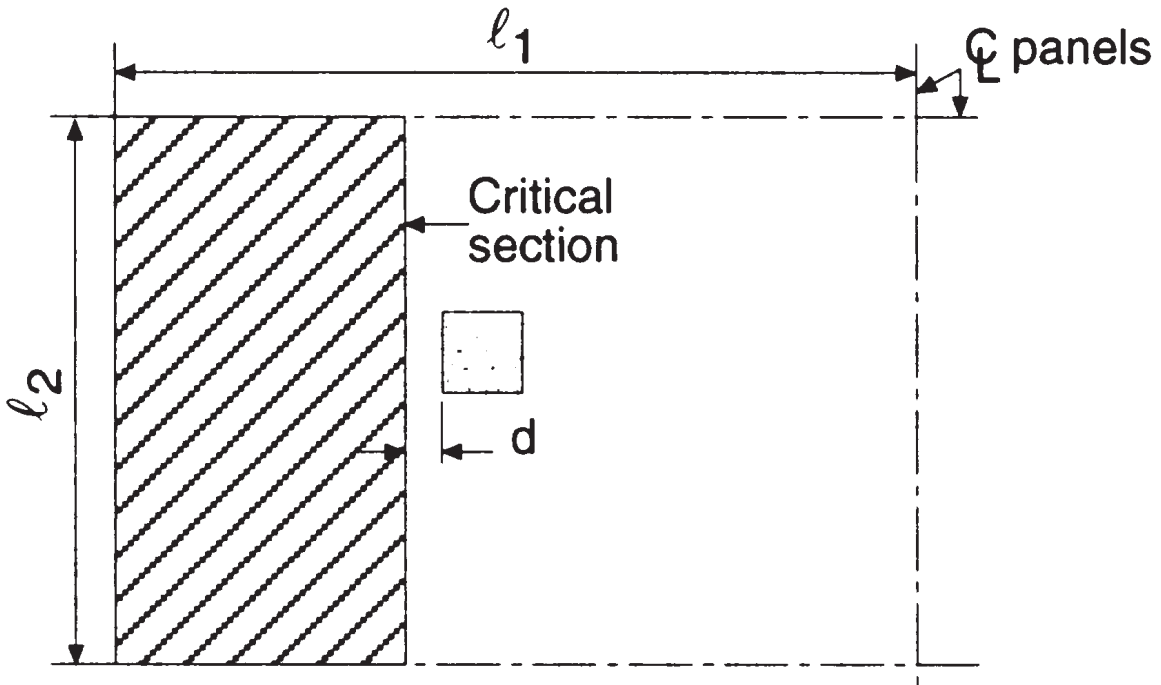
Abbildung 5. Balkenschub an der Innenstütze (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

Wo:

• Längenspanne in Längsrichtung, \({l_1 = 6,0m }\)
• Längenspanne in Querrichtung, \({l_2 = 4,0m}\)
• Gesamtes Nebenflussgebiet, Scherung in Längsrichtung \({A_t = l_2 times (\frac{l_1}{2}-\frac{c_1}{2}-d) = 4,0m times (\frac{6.0m}{2}-\frac{0.50m}{2}-0.17m) = 10.32 m^2}\) (ausgewählt)
• Gesamtes Nebenflussgebiet, Scherung in Querrichtung, \({A_t = l_1 times (\frac{l_2}{2}-\frac{c_2}{2}-d) = 6,0m times (\frac{4.0m}{2}-\frac{0.50m}{2}-0.17m) = 9.48 m^2}\)
• Quadratische Säulenabmessung, \({c_1 = c_2 = 0,50 m}\)
• Abstand d, \({d = h_{Platte} – Abdeckung = 0,20 m – 0.03m = 0,17m }\)

Deshalb, Die maximale Balkenscherung in der Innenstütze beträgt

\({V_u =q_utimes A_t =12,56 {\frac{kN}{m^2}}\mal 10.32 m^2 = 129.62 kN }\)

Dies wird mit der Scherfestigkeit verglichen, \({\phi_sV_c}\)

• Betonfestigkeit, \({f’_c = 25 MPa}\)
• Streckgrenze des Bewehrungsstahls, \({f_y = 420 MPa}\)
• \({\phi_s = 0.75}\)
• \({\phi_sV_c = 0,17phi_slambdasqrt(f’_c) b_w d; b_w=l_2}\)

\({\phi_sV_c = 0,17times 0,75times 1times sqrt(25 MPa) \mal 4000 mmtimes 170 mm = 433.50 kN }\)

Wir können sehen, dass der Scherwiderstand größer ist als der Scherbedarf: \({\phi_sV_c = 433.50 kN > V_u = 129.62 kN }\) OK!.

Gemäß den folgenden Bildern, Wir müssen die Durchstanzkapazität und die Kraft berechnen, der der Beton in der inneren Verbindung zwischen Decke und Stütze standhalten muss. Das Ziel des Codes bei der Durchstanzprüfung besteht darin, niedrige Scherspannungswerte aufrechtzuerhalten.

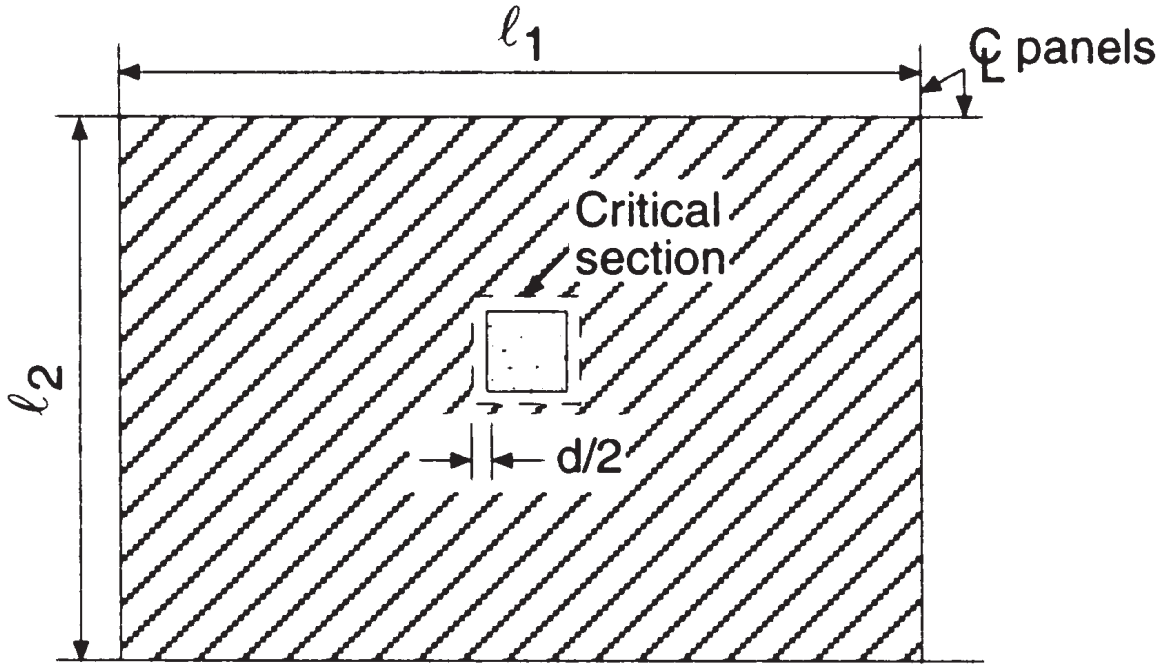
Abbildung 6. Zweiseitige Scherung an der Innensäule (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

• Gesamtes Nebenflussgebiet, Stanzschere, \({A_t = l_1 times l_2 – (c_1+d)^2 = 6,0m times 4,0m – (0.50m+0,17m)^2 = 23.55 m^2}\) (gleiche Fläche für beide Hauptrichtungen)

Die gesamte zu widerstehende Scherkraft beträgt

\({V_u =q_utimes A_t =12,56 {\frac{kN}{m^2}}\mal 23.55 m^2 = 295.79 kN }\)

Zur Ermittlung der Durchstanztragfähigkeit in einer zweiseitigen Platte, Wir werden die empirische Methode verwenden, die durch den Code ACI-318 festgelegt ist, Dabei wird die maximal verfügbare Schubspannung im wirksamen Umfang am kritischen Abschnitt berücksichtigt. Der konservativere Ausdruck für die Innensäule ist

• Durchstanzkapazität, \({\phi_sV_c = 0,33phi_slambdasqrt(f’_c) b_0 d; b_0=4times (c_1+d)}\)

Deshalb, wir haben den Scherwiderstand von

\({\phi_sV_c = 0,33times 0.75 \mal 1 \sqrt(25 MPa) \mal (4\mal (500 mm+170 mm)\mal 170mm) = 563.81 kN }\)

Wir können sehen, dass der Scherwiderstand größer ist als der Scherbedarf: \({\phi_sV_c = 563.81 kN > V_u = 295.75 kN }\) OK!.

Wir haben die einseitigen und zweiseitigen Schubanforderungen an der inneren Stützenverbindung überprüft. Da beide Anforderungen geringer sind als ihre jeweiligen Kapazitäten oder Widerstände, Wir werden nun mit der Berechnung der Hauptbewehrungsbewehrung für die Plattenbiegung fortfahren.

Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!

Melden Sie sich bei SkyCiv an!

Gesamtfaktoriertes statisches Moment pro Spanne.

Das maximale Moment, das in einen Doppelträger mit festem Ende entwickelt werden kann, ist ein isostatisches Moment gleich \({M=frac{wtimes {l_1}^ 2}{8}}\) (Siehe Abbildung 6).

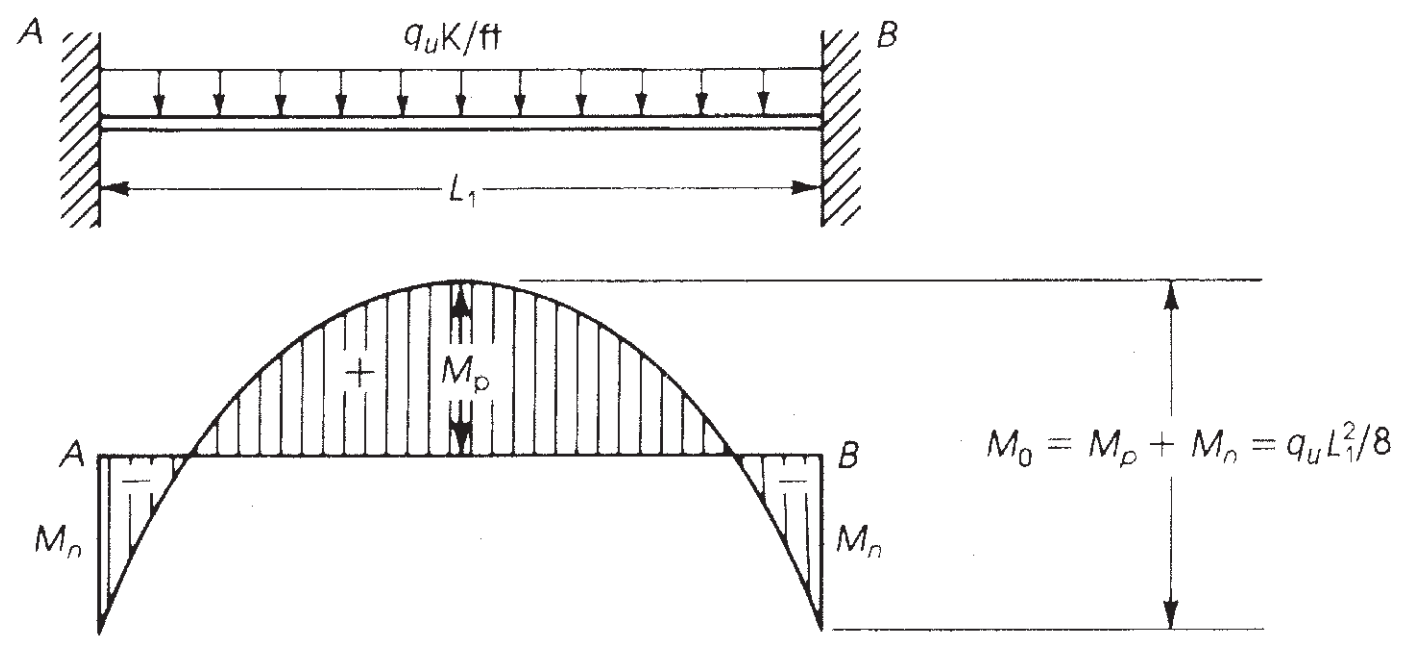
Abbildung 7. Biegemoment in einem Festbalken. (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

ACI-18 übernimmt dieses Prinzip und, für die Direct-Design-Methode (DDM), legt das maximal zu berücksichtigende statische Moment pro Feld fest \({M_0}\)

Längsrichtung:

• \({M_0 = frac {q_utimes l_2times {l_{n,1}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{kN}{m^2}}\mal 4,0mmal (6m-0.50m)^ 2}{8}=189,97 kN-m}\)

Querrichtung:

• \({M_0 = frac {q_utimes l_1times {l_{n,2}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{kN}{m^2}}\mal 6,0mmal (4m-0.50m)^ 2}{8}=115,40 kN-m}\)

Der nächste Schritt besteht darin, dieses Gesamtmoment unter Berücksichtigung des Paneeltyps zuzuweisen, innen oder außen. (Siehe Abbildung 7). Danach, da die Spannweiten durchgehend sind, Es ist notwendig, auch den Moment in positiv und negativ zu unterteilen. Letzteres ist auf den Bildern zu sehen 8 sowie 9.

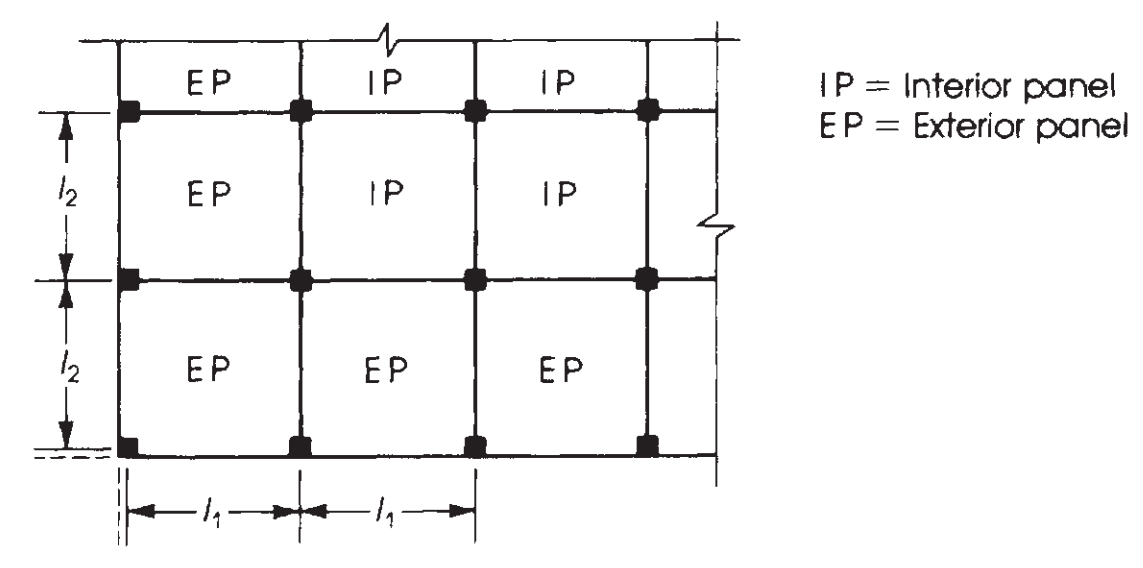
Abbildung 8. Definition von Paneelen entsprechend ihrer relativen Position in einem Deckenplan. (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

 

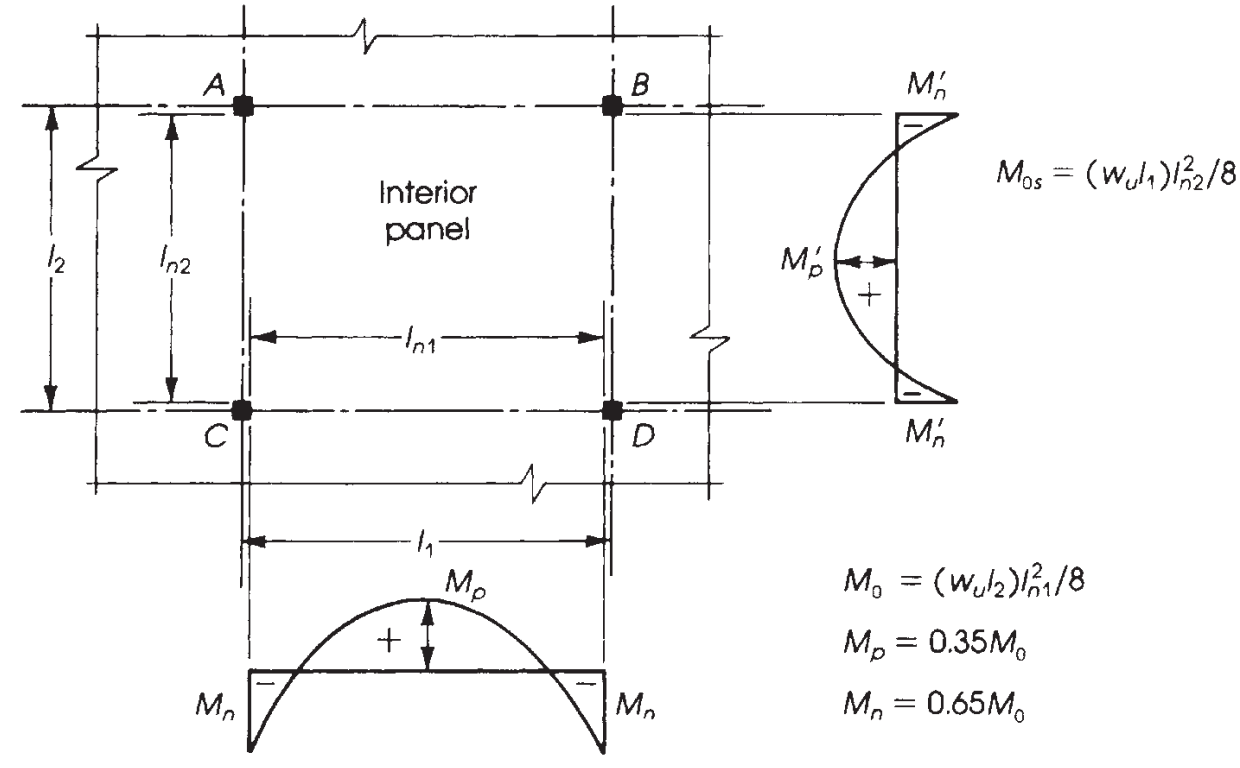
Abbildung 9. Momentenverteilung in einer Innenverkleidung. (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

 

Es ist wichtig, die richtige Momentenverteilung je nach der von uns entworfenen Platte zu kennen. In diesem Beispiel, Wir haben den letzten Fall im folgenden Bild (Zahl 9), “Keine Balken,” Wird auf einer Flachdecke oder Massivdecke ohne Balken angebracht, weder am Rand noch zwischen Stützen.

Der Hauptunterschied in den fünf in der Abbildung dargestellten Fällen 9 ist der Momentenanteil, der auf Außenpaneelen zugewiesen werden soll, wobei die relative Beschränkung am Ende die zu berechnenden Werte verändert.

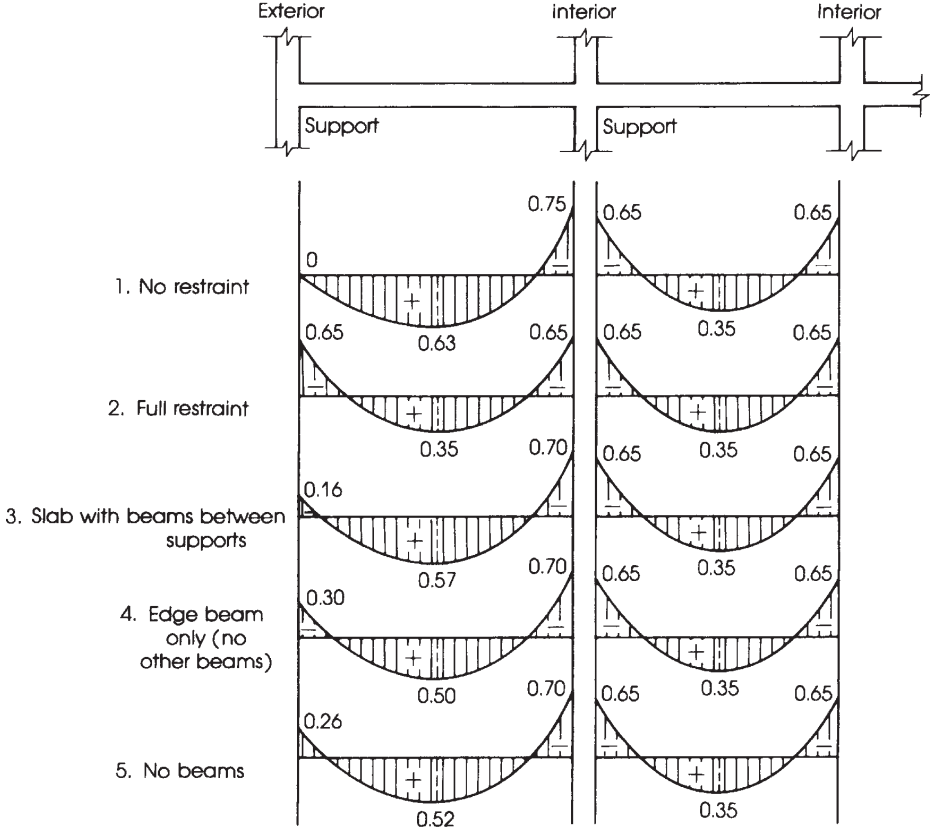
Abbildung 10. Verteilung des gesamten statischen Moments in negative und positive Spannmomente. (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

Verteilung des gesamten faktorisierten Moments \({M_0}\) pro Spanne in negative und positive Momente.

Einmal \({M_0}\) wurde berechnet, Es ist an der Zeit, in jedem Designstreifen den Anteil der Momente in positive und negative zuzuordnen, das ist, Säulen- und Mittelstreifen. Für mehr Klarheit, Zahl 10 hilft dabei, den geeigneten Faktor anzugeben, der bei der Verteilung des Gesamtmoments berücksichtigt werden soll.

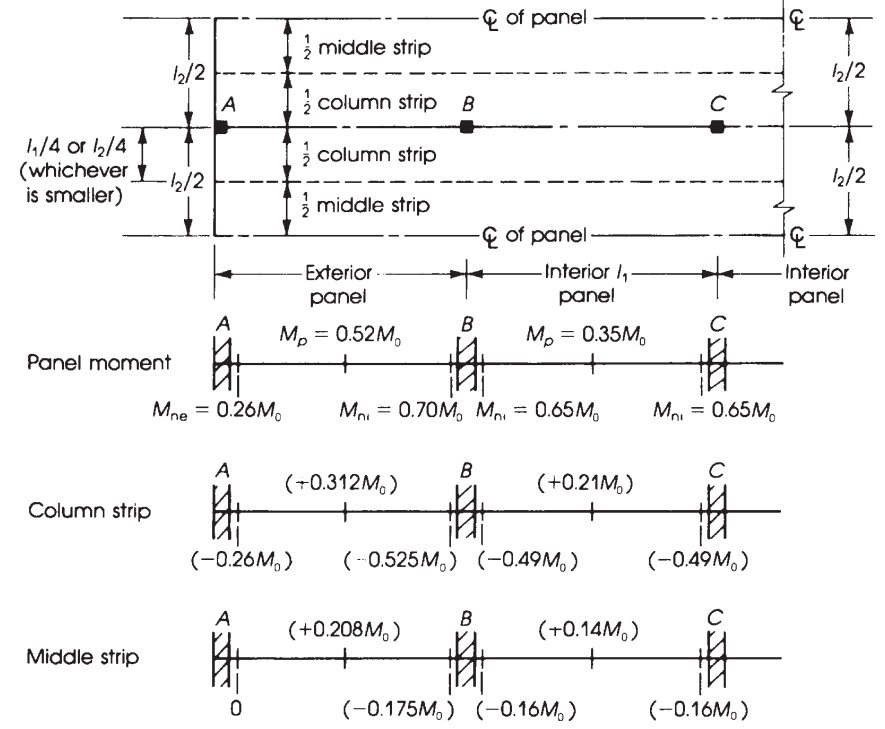
Abbildung 11. Breite des äquivalenten starren Rahmens und Momentenverteilung in Flachdecken. (Nadim Hassoun und Akthem AI-Manaseer, “Konstruktionsbetontheorie und -design”)

Unter Verwendung der in der Abbildung angegebenen vorherigen Faktoren 10, Wir erhalten in der folgenden Tabelle das ultimative Moment.

Längsrichtung: \({M_0 = 189.97 kN-m}\)

Spanne (ES:Außen, IS:Innere)	Totaler Moment (kN-m)	Stützenstreifenmoment (kN-m)	Moment im Mittelstreifen (kN-m)
Äußeres negatives ES	0.26M0=49,39	0.26M0=49,39	0
Positives ES	0.52M0=98,78	0.31M0=58,89	0.21M0=39,89
Innen negativ ES	0.70M0=132,98	0.53M0=100,68	0.17M0=32,29
Positiver IS	0.35M0=66,49	0.21M0=39,89	0.14M0=26,60
Negativer IS	0.65M0=123,48	0.49M0=93,09	0.16M0=30,40

Mit dem Moment einmal verteilt, Es ist an der Zeit, die Stahlbewehrung zu bestimmen, die in der Platte angebracht werden soll. Wir werden nur eine Berechnung entwickeln und dann alle Ergebnisse in einer Tabelle zusammenfassen.

Moment in der äußeren negativen Spanne im Stützenstreifen, \({M_u = 49.39 kN-m}\)

• Angenommener spannungsgesteuerter Abschnitt. \({\phi_f = 0.9}\)
• Breite des Säulenstreifens, \({b=2,0m}\)
• Bereich der Stahlverstärkung, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{49.39kN-m}{0.9\mal 0.9(0.17m)\mal 420 MPa}=853,996 {mm}^ 2}\)
• \({\rho_{Mindest} = 0.0018}\). Mindestbewehrungsfläche aus Stahl, \({EIN_{s,Mindest}=rho_{Mindest}\mal bmal d = 0.0018 \mal 2,0m times 0,17m =612 {mm}^ 2}\). Jetzt, Überprüfen Sie, ob sich der Abschnitt spannungsgesteuert verhält.
• \({a = frac{A_stimes f_y}{0.85\mal f’cmal b} = frac{853.996 {mm}^2times 420 MPa}{0.85\mal 25 MPatimes 2,0 m }= 8.439 mm}\)
• \({c = frac{ein}{\beta_1}= frac{8.439 mm}{0.85} = 9,929 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\mal d – 0.003 = (\frac{0.003}{9.929mm})\mal 170mm – 0.003 = 0.048 > 0.005 }\) OK!, Es handelt sich um einen Abschnitt mit kontrollierter Spannung!.

Spanne(ES:Außen, IS:Innere)	Stützenstreifenmoment (kN-m)	\({EIN_{s,kalk} ({mm}^ 2)}\)	\({EIN_{s,Mindest} ({mm}^ 2)}\)	\({ein (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Äußeres negatives ES	49.39	853.996	612.0	8.439	9.929	0.048 > 0.005!
Positives ES	58.89	1018.259	612.0	10.063	11.839	0.040 > 0.005!
Innen negativ ES	100.68	1740.844	612.0	17.204	20.24	0.022 > 0.005!
Positiver IS	39.89	689.733	612.0	6.816	8.019	0.06 > 0.005!
Negativer IS	93.09	1609.607	612.0	15.907	18.714	0.024 > 0.005!

Moment im äußeren positiven Bereich im Mittelstreifen, \({M_u = 39.89 kN-m}\)

• Angenommener spannungsgesteuerter Abschnitt. \({\phi_f = 0.9}\)
• Mittlere Streifenbreite, \({b=2,0m}\)
• Bereich der Stahlverstärkung, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{39.89kN-m}{0.9\mal 0.9(0.17m)\mal 420 MPa}=689,733 {mm}^ 2}\)
• \({\rho_{Mindest} = 0.0018}\). Mindestbewehrungsfläche aus Stahl, \({EIN_{s,Mindest}=rho_{Mindest}\mal bmal d = 0.0018 \mal 2,0m times 0,17m =612 {mm}^ 2}\). Jetzt, Überprüfen Sie, ob sich der Abschnitt spannungsgesteuert verhält.
• \({a = frac{A_stimes f_y}{0.85\mal f’cmal b} = frac{689.766 {mm}^2times 420 MPa}{0.85\mal 25 MPatimes 2,0 m }= 6.816 mm}\)
• \({c = frac{ein}{\beta_1}= frac{6.816 mm}{0.85} = 8.019 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\mal d – 0.003 = (\frac{0.003}{8.019mm})\mal 170mm – 0.003 = 0.0605 > 0.005 }\) OK!, Es handelt sich um einen Abschnitt mit kontrollierter Spannung!.

Spanne(ES:Außen, IS:Innere)	Mittlerer Strip-Moment (kN-m)	\({EIN_{s,kalk} ({mm}^ 2)}\)	\({EIN_{s,Mindest} ({mm}^ 2)}\)	\({ein (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Äußeres negatives ES	0	0.00	612.0	6.048	7.115	0.069 > 0.005!
Positives ES	39.89	689.733	612.0	6.816	8.019	0.061 > 0.005!
Innen negativ ES	32.29	558.322	612.0	6.048	7.115	0.069 > 0.005!
Positiver IS	26.60	459.937	612.0	6.048	7.115	0.069 > 0.005!
Negativer IS	30.40	525.642	612.0	6.048	7.115	0.069 > 0.005!

Querrichtung: \({M_0 = 115.40 kN-m}\)

Spanne (ES:Außen, IS:Innere)	Totaler Moment (kN-m)	Stützenstreifenmoment (kN-m)	Moment im Mittelstreifen (kN-m)
Äußeres negatives ES	0.26M0=30,00	0.26M0=30,00	0
Positives ES	0.52M0=60,00	0.31M0=35,77	0.21M0=24,23
Innen negativ ES	0.70M0=80,78	0.53M0=61,16	0.17M0=19,62
Positiver IS	0.35M0=40,39	0.21M0=24,23	0.14M0=16,16
Negativer IS	0.65M0=75,01	0.49M0=56,55	0.16M0=18,46

Mit dem Moment einmal verteilt, Es ist an der Zeit, die Stahlbewehrung zu bestimmen, die in der Platte angebracht werden soll. Wir werden nur eine Berechnung entwickeln und dann alle Ergebnisse in einer Tabelle zusammenfassen.

Moment in der äußeren negativen Spanne im Stützenstreifen, \({M_u = 30.00 kN-m}\)

• Angenommener spannungsgesteuerter Abschnitt. \({\phi_f = 0.9}\)
• Breite des Säulenstreifens, \({b=2,0m}\)
• Bereich der Stahlverstärkung, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{30.00kN-m}{0.9\mal 0.9(0.17m)\mal 420 MPa}=518,726 {mm}^ 2}\)
• \({\rho_{Mindest} = 0.0018}\). Mindestbewehrungsfläche aus Stahl, \({EIN_{s,Mindest}=rho_{Mindest}\mal bmal d = 0.0018 \mal 2,0m times 0,17m =612 {mm}^ 2}\). Jetzt, Überprüfen Sie, ob sich der Abschnitt spannungsgesteuert verhält.
• \({a = frac{A_stimes f_y}{0.85\mal f’cmal b} = frac{518.726 {mm}^2times 420 MPa}{0.85\mal 25 MPatimes 2,0 m }= 6.048 mm}\)
• \({c = frac{ein}{\beta_1}= frac{6.048 mm}{0.85} = 7,115 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\mal d – 0.003 = (\frac{0.003}{7.115mm})\mal 170mm – 0.003 = 0.069 > 0.005 }\) OK!, Es handelt sich um einen Abschnitt mit kontrollierter Spannung!.

Spanne(ES:Außen, IS:Innere)	Stützenstreifenmoment (kN-m)	\({EIN_{s,kalk} ({mm}^ 2)}\)	\({EIN_{s,Mindest} ({mm}^ 2)}\)	\({ein (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Äußeres negatives ES	30.00	518.726	612.0	6.048	7.115	0.069 > 0.005!
Positives ES	35.77	618.494	612.0	6.112	7.191	0.068 > 0.005!
Innen negativ ES	61.16	1057.509	612.0	10.451	12.295	0.038 > 0.005!
Positiver IS	24.23	418.958	612.0	6.048	7.115	0.069 > 0.005!
Negativer IS	56.55	977.799	612.0	9.663	11.368	0.042 > 0.005!

Moment im äußeren positiven Bereich im Mittelstreifen, \({M_u = 24.23 kN-m}\)

• Angenommener spannungsgesteuerter Abschnitt. \({\phi_f = 0.9}\)
• Breite des Säulenstreifens, \({b=4,0m}\)
• Bereich der Stahlverstärkung, \({A_s = frac{M_u}{\phi_ftimes 0,9dtimes fy}= frac{24.23 kN-m}{0.9\mal 0.9(0.17m)\mal 420 MPa}=418,958 {mm}^ 2}\)
• \({\rho_{Mindest} = 0.0018}\). Mindestbewehrungsfläche aus Stahl, \({EIN_{s,Mindest}=rho_{Mindest}\mal bmal d = 0.0018 \mal 4,0m times 0,17m =1224 {mm}^ 2}\). Jetzt, Überprüfen Sie, ob sich der Abschnitt spannungsgesteuert verhält.
• \({a = frac{A_stimes f_y}{0.85\mal f’cmal b} = frac{1224 {mm}^2times 420 MPa}{0.85\mal 25 MPatimes 4,0 m }= 6.048 mm}\)
• \({c = frac{ein}{\beta_1}= frac{6.048 mm}{0.85} = 7.115 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\mal d – 0.003 = (\frac{0.003}{7.115mm})\mal 170mm – 0.003 = 0.069 > 0.005 }\) OK!, Es handelt sich um einen Abschnitt mit kontrollierter Spannung!.

Spanne(ES:Außen, IS:Innere)	Mittlerer Strip-Moment (kN-m)	\({EIN_{s,kalk} ({mm}^ 2)}\)	\({EIN_{s,Mindest} ({mm}^ 2)}\)	\({ein (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Äußeres negatives ES	0.00	0.00	1224.00	6.048	7.115	0.069 > 0.005!
Positives ES	24.23	418.958	1224.00	6.048	7.115	0.069 > 0.005!
Innen negativ ES	19.62	339.247	1224.00	6.048	7.115	0.069 > 0.005!
Positiver IS	16.16	279.420	1224.00	6.048	7.115	0.069 > 0.005!
Negativer IS	18.46	319.189	1224.00	6.048	7.115	0.069 > 0.005!

Wenn Sie neu bei SkyCiv sind, Melden Sie sich an und testen Sie die Software selbst!

Melden Sie sich bei SkyCiv an!

SkyCiv S3D-Designmodul

In diesem Abschnitt, Wir beschreiben das Designergebnis mithilfe des in SkyCiv enthaltenen Moduls für Plattendesign. Wir erklären nicht, wie die Struktur modelliert und analysiert wird (für diese, Weitere Artikel zu diesem Thema finden Sie in unserer Dokumentation: So modellieren Sie eine Struktur in SkyCiv?, So wenden Sie Lasten in meinem Gebäudemodell an? sowie So führen Sie eine lineare elastische Analyse durch?)

Um ein genaues Designergebnis zu erzielen, ist es zweckmäßig, ein feines Netz auf die Platten aufzubringen. Für mehr Klarheit schauen Sie sich bitte das folgende Bild an.

Abbildung 12. Auf Platten wird ein feineres Netz aufgetragen

Der nächste Schritt besteht darin, das Designmodul auszuführen und die Optionen auszuwählen, mit denen eine optimierte Stahlbewehrungsfläche berechnet wird.

Abbildung 13. Definition der Plattenbetoneigenschaften vor der Entwurfsoptimierung.

Abbildung 14 stellt die Ausrichtung der lokalen Achsen der Platte dar. Weil lokale Achse 3 ist nach unten, bleibt die “oben” ist der Boden, und das “Unterseite” wird die Spitze sein, Somit werden die Daten korrekt aus dem Design übernommen.

Ein weiterer wichtiger Faktor ist die Maschenweite der Platte; Es handelt sich um ein quadratisches Plattenelement mit den Grundrissabmessungen 500 mm x 500 mm. SkyCiv S3D gibt die Bewehrungsfläche als integrierten Wert pro finitem Element an. So, wenn wir die gesamte Bewehrungsfläche einer Säule oder eines Mittelstreifens ermitteln möchten, Wir müssen den Mittelwert aus der Anzahl der Elemente berechnen, die die zu analysierende Streifenbreite summieren. Ein Träger, für den Säulenstreifen, Vier Elemente werden berücksichtigt (4×0.5m = 2m).

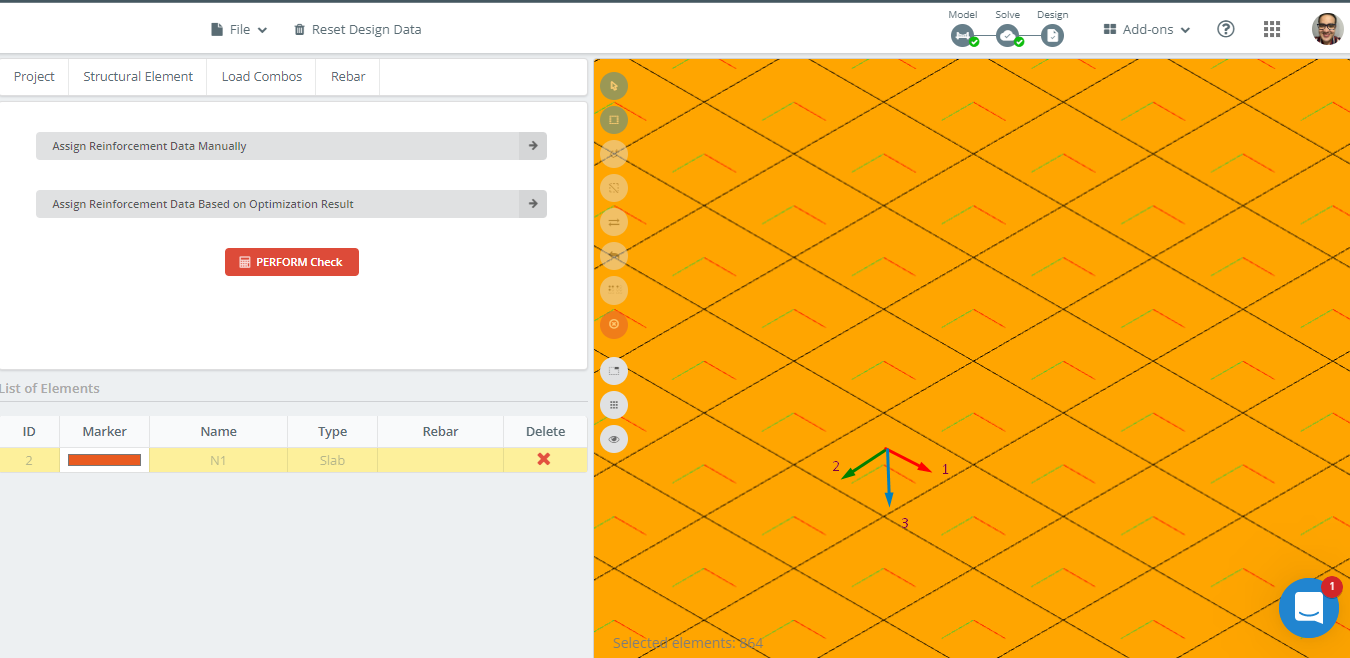
Abbildung 14. Lokale Achsenorientierung im Beispiel einer Platte.

Zuerst, Wir analysieren die erforderliche Verstärkungsfläche entlang der Längsrichtung in der Achse 1.

Säulenstreifen

• Äußerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(119.09\mal 2 + 952.72 + 833.64 )\frac{{mm}^ 2}{m} \mal 0,50m = 1012.27 {mm}^ 2}\)
• Äußerer positiver Moment (untere Verstärkung): \({EIN_{s,bot} = 4*463.90 \frac{{mm}^ 2}{m}\mal 0,50m = 927.80 {mm}^ 2}\)
• Äußerer, innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(1071.82\mal 2 +714.54 \mal 2 )\frac{{mm}^ 2}{m} \mal 0,50m = 1786.36 {mm}^ 2}\)
• Positiver Moment im Innenraum(untere Verstärkung): \({EIN_{s,bot} = 4*309.27 \frac{{mm}^ 2}{m}\mal 0,50m = 618.54 {mm}^ 2}\)
• Innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(714.54\mal 2 +952.73 \mal 2 )\frac{{mm}^ 2}{m} \mal 0,50m = 1667.27 {mm}^ 2}\)

Mittelstreifen

• Äußerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(119.09\mal 4)\frac{{mm}^ 2}{m} \mal 0,50m = 238.18 {mm}^ 2}\)
• Äußerer positiver Moment (untere Verstärkung): \({EIN_{s,bot} = (463.90\mal 2 +412.36 \mal 2 ) \frac{{mm}^ 2}{m}\mal 0,50m = 876.26 {mm}^ 2}\)
• Äußerer, innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(357.27\mal 2 +476.36 \mal 2 )\frac{{mm}^ 2}{m} \mal 0,50m = 833.63 {mm}^ 2}\)
• Positiver Moment im Innenraum(untere Verstärkung): \({EIN_{s,bot} = 4*257.72 \frac{{mm}^ 2}{m}\mal 0,50m = 515.44 {mm}^ 2}\)
• Innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(357.27\mal 2 +476.36 \mal 2 )\frac{{mm}^ 2}{m} \mal 0,50m = 833.63 {mm}^ 2}\)

Abbildung 15. Optimierungsergebnisse in Richtung “1” und die Oberseite (Unterseite, Genau genommen).

Abbildung 16. Optimierungsergebnisse in Richtung “1” und die Unterseite (Oberseite, Genau genommen).

Schließlich, Wir analysieren die erforderliche Verstärkungsfläche entlang der Querrichtung in der Achse 2.

Säulenstreifen

• Äußerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(91.55\mal 2 + 457.73 + 549.28 )\frac{{mm}^ 2}{m} \mal 0,50m = 595.055 {mm}^ 2}\)
• Äußerer positiver Moment (untere Verstärkung): \({EIN_{s,bot} = (269.68\mal 3+239.72) \frac{{mm}^ 2}{m}\mal 0,50m = 524.38 {mm}^ 2}\)
• Äußerer, innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(823.92\mal 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \mal 0,50m = 1327.43 {mm}^ 2}\)
• Positiver Moment im Innenraum(untere Verstärkung): \({EIN_{s,bot} = (179.79\mal 3+149.82) \frac{{mm}^ 2}{m}\mal 0,50m = 344.60 {mm}^ 2}\)
• Innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(823.92\mal 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \mal 0,50m = 1327.43 {mm}^ 2}\)

Mittelstreifen

• Äußerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(183.09\mal 2+91,55times 6)\frac{{mm}^ 2}{m} \mal 0,50m = 457.74 {mm}^ 2}\)
• Äußerer positiver Moment (untere Verstärkung): \({EIN_{s,bot} = (209.75\mal 2 +179.79 \mal 2 +149.82 \mal 4) \frac{{mm}^ 2}{m}\mal 0,50m = 689.18{mm}^ 2}\)
• Äußerer, innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(274.64\mal 2+91,55times 6)\frac{{mm}^ 2}{m} \mal 0,50m = 549.29 {mm}^ 2}\)
• Positiver Moment im Innenraum(untere Verstärkung): \({EIN_{s,bot} = (119.86\mal 4 + 89.89\mal 4) \frac{{mm}^ 2}{m}\mal 0,50m = 419.50 {mm}^ 2}\)
• Innerer negativer Moment (obere Verstärkung): \({EIN_{s,oben} =(274.64\mal 2+91,55times 6 )\frac{{mm}^ 2}{m} \mal 0,50m = 549.29 {mm}^ 2}\)

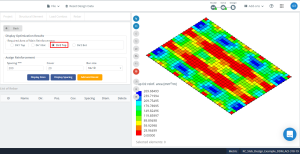
Abbildung 17. Optimierungsergebnisse in Richtung “2” und die Oberseite (Unterseite, Genau genommen).

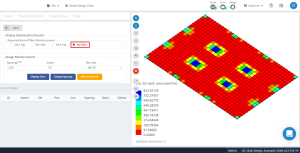
Abbildung 18. Optimierungsergebnisse in Richtung “2” und die Unterseite (Oberseite, Genau genommen).

 

Ergebnisvergleich

Die folgende Tabelle zeigt die Ergebnisse für das DDM (“Direkte Designmethode”) und die S3D-Stahlbewehrungsoptimierung.

Spanne (ES:Außen, IS:Innere)	Säulenstreifen (S3D-Design) \({Als ({mm}^ 2)}\)	Säulenstreifen (ACI-318 DDM) \({Als ({mm}^ 2)}\)	% Diff	Mittelstreifen (S3D-Design) \({Als ({mm}^ 2)}\)	Mittelstreifen (ACI-318 DDM) \({Als ({mm}^ 2)}\)	% Diff
Äußeres negatives ES	1012.27	853.996	15.636	238.18	0 (612.0)	100.00
Positives ES	927.80	1018.259	9.75	876.26	689.733	21.287
Innen negativ ES	1786.36	1740.844	2.48	833.63	558.322 (612.0)	26.586
Positiver IS	618.54	689.733	11.51	515.44	459.937 (612.0)	18.734
Negativer IS	1667.27	1609.607	3.459	833.63	525.642 (612.0)	26.586

Querrichtung

Spanne (ES:Außen, IS:Innere)	Säulenstreifen (S3D-Design) \({Als ({mm}^ 2)}\)	Säulenstreifen (ACI-318 DDM) \({Als ({mm}^ 2)}\)	% Diff	Mittelstreifen (S3D-Design) \({Als ({mm}^ 2)}\)	Mittelstreifen (ACI-318 DDM) \({Als ({mm}^ 2)}\)	% Diff
Äußeres negatives ES	595.055	518.726	12.827	457.74	0 (1224)	100.00
Positives ES	524.38	618.494	17.948	689.18	418.958	39.209
Innen negativ ES	1327.43	1057.509	20.334	549.29	339.247	38.239
Positiver IS	344.60	418.958	21.578	419.50	279.42	33.392
Negativer IS	1327.43	977.799	26.339	549.29	319.189	41.891

Fazit

Wir haben in diesem Artikel gezeigt, dass das SkyCiv-Modul für Plattenkonstruktion die Stahlbewehrung für Biegeplatten gemäß dem Code ACI-318-19 berechnet. Vergleich der Ergebnisse der Analyse in den Spaltenstreifen, wo wegen ihrer relativen Steifigkeit, Die Momente sind hochkonzentriert, Die Unterschiede zwischen Handberechnungen und Optimierung durch S3D runden einen Wert von ab 10 – 15%. Diese Praktikabilität weist auf eine hervorragende Übereinstimmung zwischen Analyse- und Entwurfsverfahren hin.

Für Mittelstreifen, Die Ergebnisse unterscheiden sich etwas stärker, da der Code den Rest des Moments erst nach der Aufnahme der entsprechenden Spaltenstreifen zuordnet. Dies wirkt sich auf die Übereinstimmung aus, wenn wir sie mit der Analyse der Software vergleichen, was genauer ist.

Neu bei SkyCiv? Melden Sie sich an und testen Sie die Software selbst!

Melden Sie sich bei SkyCiv an!