Schätzung der Pfahlkapazität
Die Schätzung der Tragfähigkeit des Pfahls ist erforderlich, um die maximale Axiallast zu bestimmen, die der Pfahl tragen kann. Die ultimative Tragfähigkeit des Pfahls (Qu) entspricht der Summe der Endtragfähigkeiten (Qp) und Reibungswiderstand (Fragen), dargestellt durch Abb. 1 und Gl. 1. Zahlreiche veröffentlichte Studien und Praktiken bestimmen die Endtragfähigkeit und den Reibungswiderstand des Pfahls. Dieser Artikel konzentriert sich auf verschiedene Methoden zur Schätzung der endgültigen Pfahlkapazität.
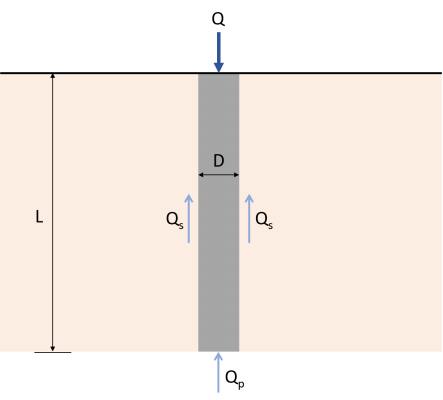
\( {Q.}_{u} = {Q.}_{p} + {Q.}_{s} \) (1)
Q.u : Ultimative Tragfähigkeit
Q.p : Endlagertragfähigkeit
Q.s : Reibungswiderstand der Haut
Universelle Gleichungen für Qp und Qs
\( {Q.}_{p} = {Ein}_{p} \mal {q}_{p} \) (2)
\( {q}_{p} = (c times {N.}_{c}) + (q’ \mal {N.}_{q}) + (\Gamma times D times {N.}_{\p-Delta-Effekte}) \) (3)
\( {Q.}_{p} = {Ein}_{p} \mal[ (c times {N.}_{c}) + (q’ \mal {N.}_{q}) ] \) (4)
Der gesamte Reibungswiderstand des Pfahls, die sich entlang ihrer Länge entwickelt, kann mit dieser Gleichung berechnet werden:
\( {Q.}_{s} = ∑ (p × ΔL × f) \) (5)
p: Umfang des Pfahls
L: Inkrementelle Pfahllänge, über die p und f gemessen werden
f: Reibungswiderstand der Einheit in jeder Tiefe
Methoden zur Schätzung von Qp
Meyerhofs Methode
Sandiger Boden
Laut Meyerhof, der Einheitspunktwiderstand (qp) von Pfählen im Sand nimmt im Allgemeinen mit der Einbettungslänge zu, bis sie beim Einbettungsverhältnis ihren Maximalwert erreicht (L/D) einen kritischen Wert erreicht. Kritisches Einbettungsverhältnis (L/D)Einstellungen für Biege-Torsionsknicken variiert normalerweise von 16 zu 18. Bei dieser Methode, Es wird davon ausgegangen, dass Pfähle im Sand keine Kohäsion aufweisen (c ≈ 0), und der Einheitspunktwiderstand sollte den Grenzpunktwiderstand nicht überschreiten (ql), was durch Gl. gegeben ist. 7. Der Tragfähigkeitsfaktor (Bodenkohäsion an der Pfahlspitze q) Die Werte sind direkt proportional zum Bodenreibungswinkel der tragenden Schicht (Tabelle 1). Basierend auf Meyerhofs Theorie, die universelle Gleichung für Qp (Gleichung 4) kann vereinfacht werden zu:
\( {Q.}_{p} = {Ein}_{p} \mal (q’ \mal {N.}_{q}) \leq ({Ein}_{p} \mal {q}_{l}) \) (6)
\( {q}_{l} = 0.5 \mal {p}_{ein} \mal {N.}_{q} \mal braun (\Phi’) \) (7)
ql : Grenzpunktwiderstand
pein: Luftdruck (≈100 kN/m2)
\( \phi’): Effektiver Bodenreibungswinkel an der Pfahlspitze
Tabelle 1: Interpolierte Werte von Nq (Meyerhofs Theorie)
Tonerde
Gleichung 4 kann auch die Endtragfähigkeit von Pfählen in tonigen oder bindigen Böden berechnen (φ ≈ 0). Da der Bodenreibungswinkel und der Tragfähigkeitsfaktor vernachlässigt werden (N.c) hat einen konstanten Wert von 9 für bindige Böden, Gleichung 4 kann geschrieben werden als::
\( {Q.}_{p} = {Ein}_{p} \mal c times {N.}_{c} = 9 \mal c times {Ein}_{p} \) (8)
Vesics Methode
Vesics Methode zur Berechnung der Endtragfähigkeit auf sandigen oder tonigen Böden basiert auf seiner Theorie der Hohlraumausdehnung.
Sandiger Boden
Basierend auf seiner Theorie, Die Endtragfähigkeit von Pfählen im Sand kann anhand der folgenden Gleichungen abgeschätzt werden:
\( {Q.}_{p} = {Ein}_{p} \mal bar{\Sigma’}_{Das} \mal {N.}_{\Sigma} \) (9)
\(\Bar{\Sigma’}_{Das} = frac{1 + (2 \mal {K.}_{Das})}{3} \mal q’) (10)
\( {K.}_{Das} = 1 – sin \phi’\) (11)
\( {N.}_{\Sigma} = frac{3 \mal {N.}_{q}}{1 + (2 \mal {K.}_{Das})} \) (12)
\(\Bar{\Sigma’}_{Das} \) : Mittlere effektive Bodennormalspannung auf Höhe der Pfahlspitze
Ist: Erddruckkoeffizient im Ruhezustand
Ns: Tragfähigkeitsfaktor
Tonerde
Das Gleiche gilt für Meyerhofs Methode, Gl. 4 ist auch zur Berechnung der Endtragfähigkeit von Pfählen aus Ton anwendbar. Jedoch, der Wert des Tragfähigkeitsfaktors (N.c) ist ein Faktor des Steifigkeitsindex (Ir). Nach seiner Theorie der Ausdehnung von Hohlräumen, N.c und ichr kann geschätzt werden durch:
\( {N.}_{c} = (\frac{4}{3}) \mal [ln({I}_{r}) + 1] + \frac{\Pi}{2} + 1 \) (13)
\( {I}_{r} = frac{{E.}_{s}}{3 \mal c} \) (Für φ ≈ 0)(14)
Ir: Steifigkeitsindex
E.s: Elastizitätsmodul des Bodens
Die Methode von Coyle und Castello (Sandiger Boden)
Bezogen auf 24 groß angelegte Feldbelastungsversuche von Rammpfählen im Sand, Coyle und Castello schlugen vor, dass die Endtragfähigkeit von Pfählen mithilfe von Gleichung 15 berechnet werden kann. Die Werte des Tragfähigkeitsfaktors (Bodenkohäsion an der Pfahlspitze q) ist ein Faktor beider Einbettungsverhältnisse (L/D) und der Bodenreibungswinkel (Phi'), wie in Abb. 2
\( {Q.}_{p} = {Ein}_{p} \mal (q’ \mal {N.}_{q}) \) (15)
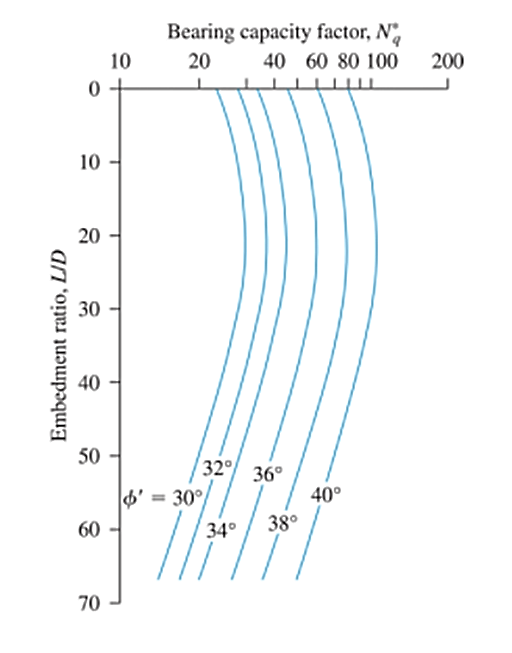
Abbildung 2: Variation von Nq mit L/D & Phi’ (Nach Coyle neu gezeichnet & Castello, 1981)
Quelle: Das, Braja. Grundlagen des Grundbaus (7th Ausgabe, S.564)
Methoden zur Schätzung von Qs
Reibungswiderstand von Pfählen im Sand
Die Einheit des Reibungswiderstands von Pfählen im Sand, wie in Gl. gezeigt. 5, berücksichtigt mehrere Faktoren, die recht schwer zu berechnen sind. Darin ist der Erddruckbeiwert enthalten (K.) & Reibungswinkel Boden-Haufen, Beide haben unterschiedliche Werte, je nachdem, welcher Ansatz verwendet wird oder welche Bodendaten verfügbar sind.
\( f = Ktimes {\Sigma}_{Das}’ \mal braun (\p-Delta-Effekte) \) (15)
K.: Effektiver Erddruckkoeffizient
σ’Das: Effektive Vertikalspannung in der betrachteten Tiefe
D: Reibungswinkel Boden-Haufen
Im Folgenden werden die verschiedenen Methoden zur Schätzung des effektiven Erddruckkoeffizienten und der Werte des Bodenreibungswinkels beschrieben. Diese Variablen sind ein Faktor des Bodenreibungswinkels (Phi') oder Pfahltyp.
Effektiver Erddruckkoeffizient
Der Boden übt seitlichen Erddruck auf die Pfahloberfläche aus. Dieser Druck muss bei der Konstruktion oder Stabilitätsanalyse berücksichtigt werden. Im Folgenden werden die verschiedenen Methoden zur Bestimmung der Erddruckkoeffizienten beschrieben, um den Einheitsreibungswiderstand von Pfählen im Sand zu berechnen.
NAVFAC DM 7.2
| Pfahltyp | Kompression | Erheben |
|---|---|---|
Tabelle 2: Erddruckkoeffizient, K. (NAVFAC DM 7.2)
Durchschnittliche K-Methode
Der Erddruckkoeffizient (K.) kann auch anhand des Durchschnitts des Erddruckkoeffizienten im Ruhezustand ermittelt werden (K.0), aktiver Erddruck (K.ein), und passiver Erddruck (K.p), wie aus den Gleichungen hervorgeht 16-19.
\( K =frac{{K.}_{0} + {K.}_{ein} + {K.}_{p}}{3} \) (16)
\( (K.)_{0} =1 – sin phi \) (17)
\( (K_{ein} =1 – {bräunen}^{2}( \frac{45 – \phi}{2}) \) (18)
\( (K_{p} =1 + {bräunen}^{2}( \frac{45 + \phi}{2}) \) (19)
Mansur und Hunter (1970)
Basierend auf verschiedenen Ergebnissen von Feldbelastungstests, Mansur und Hunter ermittelten die Werte des Erddruckkoeffizienten mit den entsprechenden Pfahltypen.
| Pfahltyp | K. |
|---|---|
Tabelle 3: Erddruckkoeffizient, K. (Mansur und Hunter, 1970)
Reibungswinkel Boden-Haufen
Der Reibungswinkel zwischen Boden und Pfahloberfläche ist ein wesentlicher Aspekt der Fundamentkonstruktion. Praktisch, Viele Ingenieure schätzen diesen Wert als gleich an 2/3 des inneren Reibungswinkels des Bodens. Jedoch, basierend auf der Studie von Coyle und Castello in 1981, Der Boden-Haufen-Reibungswinkel entspricht ungefähr 80% des inneren Reibungswinkels des Bodens. Andererseits, NAVFAC DM7.2 nutzt diese Werte, um den Reibungswinkel zwischen Boden und Pfahl abzuschätzen:
| Pfahltyp | D |
|---|---|
Tabelle 4: Reibungswinkel Boden-Haufen (D) (NAVFAC DM 7.2)
Reibungswiderstand von Pfählen aus Ton
Die Berechnung des Reibungswiderstands von Pfählen in tonigen Böden kann aufgrund der Einführung neuer Variablen ebenso schwierig sein wie die in sandigen Böden, die auch nicht so einfach zu bestimmen sind. Jedoch, Es stehen mehrere Methoden zur Verfügung, um die Werte dieser Variablen zu ermitteln.
λ-Methode
Basierend auf der Studie von Vijayvergiya und Focht in 1972, Der gesamte Reibungswiderstand von Pfählen aus Ton kann durch Bestimmung des durchschnittlichen Einheitsreibungswiderstands des Pfahls geschätzt werden, wie durch Gleichungen gezeigt 20 und 21. Die λ-Werte ändern sich mit zunehmender Eindringtiefe des Pfahls. Tabelle 5 zeigt die Variation von λ mit der Einbettungslänge des Pfahls.
\( {f}_{von} = lambdatimes [\Bar{\Sigma’}_{Das} +( 2 \mal {c}_{u})] \) (20)
\({Q.}_{s} = p times L times {f}_{von} \) (21)
\( \Bar{\Sigma’}_{Das} \): Mittlere effektive Vertikalspannung über die gesamte Einbettungslänge
cu: Mittlere undrainierte Scherfestigkeit
| L. ( Mio.) | λ |
|---|---|
Tabelle 5: Variation von λ mit der Pfahleinbettungslänge (L.)
α-Methode
Die α-Methode legt nahe, dass der Einheitsreibungswiderstand von Pfählen dem Produkt aus der undrainierten Kohäsion der Bodenschicht und dem entsprechenden empirischen Adhäsionsfaktor entspricht (ein). Tabelle 6 zeigt den entsprechenden Wert des Adhäsionsfaktors mit dem Verhältnis von undrainierter Kohäsion und Atmosphärendruck (cu/pein).
\(f = alphatimes {c}_{u}\) (22)
Deshalb, Der Gesamtreibungswiderstand eines Pfahls in Ton kann mit dieser Methode umgeschrieben werden als:
\({Q.}_{s} = sum (f times p times Updelta L) = sum (\Alpha times {c}_{u} \mal p times Updelta L)\) (23)
| cu/pein | ein |
|---|---|
| 0.8 | |
pein = Atmosphärendruck ≈ 100 kN / m2
Tabelle 6: Variation von α (p-Delta-Effekte, Picken, und Mesri, 1996)
β-Methode
Der Porenwasserdruck um den Pfahl herum erhöht sich, wenn der Pfahl in gesättigten Ton gerammt wird. Diese Methode, basierend auf einer effektiven Stressanalyse, ist für den Langzeitgebrauch geeignet (entwässert) Analysen der Pfahltragfähigkeit unter Berücksichtigung des allmählichen Abbaus des überschüssigen Porenwasserdrucks im Laufe der Zeit. Laut Tomlinson (1971), Pfähle, die in weiche Tone gerammt werden, gehen davon aus, dass Fehler im umgeformten Boden nahe der Pfahloberfläche auftreten. Basierend auf Gl. 15, der Begriff (K × tanδ) für den Einheitsreibungswiderstand von Pfählen im Sand wird durch β dargestellt. Der Bodenreibungswinkel (D) durch einen nachgeformten entwässerten Reibungswinkel des Bodens ersetzt werden (Phi’R.). Daher wird der Einheitsreibungswiderstand von Pfählen aus Ton auf gleich geschätzt:
\(f = betatimes {\Sigma’}_{Das}\) (24)
\(\Beta = K times tan {\Phi‘}_{R.}\) (25)
Konservativ, der Erddruckkoeffizient (K.) entspricht dem Erddruckbeiwert im Ruhezustand (K.0) die für normal verfestigte Tone und überverfestigte Tone unterschiedlich ist, wie in den folgenden Gleichungen gezeigt:
\( K = {K.}_{0} = 1 – ohne {\Phi‘}_{R.}\) (Normalerweise verfestigter Ton) (26)
\( K = {K.}_{0} = (1 – ohne {\Phi‘}_{R.}) \mal sqrt(OCR)\) (Überverfestigter Ton) (27)
OCR: Überkonsolidierungsquote
Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Unser kostenloses Tool ermöglicht es Benutzern, Tragfähigkeitsberechnungen durchzuführen, ohne dass ein Download oder eine Installation erforderlich ist!
Verweise:
- Das, B.M. (2007). Grundlagen des Grundbaus (7th Ausgabe). Globales Engineering
- Rajapakse, R.. (2016). Faustregel für Pfahldesign und -konstruktion (2nd Ausgabe). Elsevier Inc.
- Tomlinson, M.J. (2004). Pfahlentwurfs- und Baupraxis (4th Ausgabe). E. & Sponser der Vereinten Nationen.


