Einzelflorausführung nach AS 2159 (2009) & 3600 (2018)

Einzelflorausführung nach AS, Einzelflorausführung nach AS. Einzelflorausführung nach AS, jedoch, Einzelflorausführung nach AS, Einzelflorausführung nach AS, Einzelflorausführung nach AS.

Einzelflorausführung nach AS (ACI 318) und australische Standards (AS 2159 & 3600).

Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Unser kostenloses Tool ermöglicht es Benutzern, Tragfähigkeitsberechnungen durchzuführen, ohne dass ein Download oder eine Installation erforderlich ist!

Foundation Design Calculator

Einzelflorausführung nach AS

Einzelflorausführung nach AS. Einzelflorausführung nach AS (R._d,G) Einzelflorausführung nach AS (R._{d,Einzelflorausführung nach AS}) Einzelflorausführung nach AS (Ö_G) Einzelflorausführung nach AS AS 2159 Sektion 4.3.1.

\({R.}_{d,G} = {Ö}_{G} × {R.}_{d,Einzelflorausführung nach AS}\) (1)

R._d,G Einzelflorausführung nach AS

R._{d,Einzelflorausführung nach AS} Einzelflorausführung nach AS

Ö_G = Geotechnischer Abminderungsfaktor

= Geotechnischer Abminderungsfaktor (R._{d,Einzelflorausführung nach AS})

= Geotechnischer Abminderungsfaktor (f_m,s ) = Geotechnischer Abminderungsfaktor.

\( {R.}_{d,Einzelflorausführung nach AS} = [{R.}_{s} × ({f}_{m,s} × {Ein}_{s} )] + ({f}_{b} × {Ein}_{b} )\) (2)

R._s = Geotechnischer Abminderungsfaktor

f_m,s = Geotechnischer Abminderungsfaktor

Ein_s = Geotechnischer Abminderungsfaktor

f_b = Geotechnischer Abminderungsfaktor

Ein_b = Geotechnischer Abminderungsfaktor

Für eine ausführlichere Anleitung, Lesen Sie unseren Artikel zum Rechnen der Hautreibungswiderstand und die Endtragfähigkeit.

Geotechnischer Reduktionsfaktor (Ö_G)

= Geotechnischer Abminderungsfaktor, wie Standortbedingungen, = Geotechnischer Abminderungsfaktor, = Geotechnischer Abminderungsfaktor. = Geotechnischer Abminderungsfaktor 0.40 zu 0.90. AS 2159 4.3.1 = Geotechnischer Abminderungsfaktor (3).

\( {Ö}_{G} = {Ö}_{= Geotechnischer Abminderungsfaktor} + [= Geotechnischer Abminderungsfaktor ({Ö}_{tf} – {Ö}_{= Geotechnischer Abminderungsfaktor})] ≥ {Ö}_{= Geotechnischer Abminderungsfaktor} \) (3)

Ö_{= Geotechnischer Abminderungsfaktor} = Geotechnischer Abminderungsfaktor

Ö_tf = Geotechnischer Abminderungsfaktor

= Geotechnischer Abminderungsfaktor

Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden. Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden 1 Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden (4) und (5). Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden 8 Unterschied zwischen verstärkt 2159.

Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden (Ötf)
Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden	0.90
Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden	0.75
Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden	0.80
Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden	0.75
Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden	0.85
Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden	0.80

Tabelle 1: Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden

Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden:

\( [object Window]{1.33 Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden}{p + 3.3} ≤ 1\) (4)

Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden:

\( [object Window]{1.13 Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden}{p + 3.3} ≤ 1\) (5)

Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden

Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden 4.3. Unterschied zwischen verstärkt 2159. Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden (Sowohl die intrinsischen Tests als auch die Testnutzenfaktoren hängen davon ab, welche Art von Belastungstests für die Pfähle verwendet werden) und eine durchschnittliche Risikobewertung des Gesamtdesigns (und eine durchschnittliche Risikobewertung des Gesamtdesigns) und eine durchschnittliche Risikobewertung des Gesamtdesigns_{= Geotechnischer Abminderungsfaktor} wie in Tabelle gezeigt 2.

und eine durchschnittliche Risikobewertung des Gesamtdesigns (Ö= Geotechnischer Abminderungsfaktor)
und eine durchschnittliche Risikobewertung des Gesamtdesigns (und eine durchschnittliche Risikobewertung des Gesamtdesigns)	Risikokategorie	Ö= Geotechnischer Abminderungsfaktor und eine durchschnittliche Risikobewertung des Gesamtdesigns	Ö= Geotechnischer Abminderungsfaktor und eine durchschnittliche Risikobewertung des Gesamtdesigns
und eine durchschnittliche Risikobewertung des Gesamtdesigns 1.5	und eine durchschnittliche Risikobewertung des Gesamtdesigns	0.67	0.76
1.5 < und eine durchschnittliche Risikobewertung des Gesamtdesigns 2.0	und eine durchschnittliche Risikobewertung des Gesamtdesigns	0.61	0.70
2.0 < und eine durchschnittliche Risikobewertung des Gesamtdesigns 2.5	Niedrig	0.56	0.64
2.5 < und eine durchschnittliche Risikobewertung des Gesamtdesigns 3.0	und eine durchschnittliche Risikobewertung des Gesamtdesigns	0.52	0.60
3.0 < und eine durchschnittliche Risikobewertung des Gesamtdesigns 3.5	Mäßig	0.48	0.56
3.5 < und eine durchschnittliche Risikobewertung des Gesamtdesigns 4.0	und eine durchschnittliche Risikobewertung des Gesamtdesigns	0.45	0.53
4.0 < und eine durchschnittliche Risikobewertung des Gesamtdesigns 4.5	Hoch	0.42	0.50
und eine durchschnittliche Risikobewertung des Gesamtdesigns > 4.5	und eine durchschnittliche Risikobewertung des Gesamtdesigns	0.40	0.47

Tabelle 2: und eine durchschnittliche Risikobewertung des Gesamtdesigns, (AS 2159 Tabelle 4.3.2)

und eine durchschnittliche Risikobewertung des Gesamtdesigns 4 Pfähle.

und eine durchschnittliche Risikobewertung des Gesamtdesigns

und eine durchschnittliche Risikobewertung des Gesamtdesigns. und eine durchschnittliche Risikobewertung des Gesamtdesigns (R._d,s) und eine durchschnittliche Risikobewertung des Gesamtdesigns, und eine durchschnittliche Risikobewertung des Gesamtdesigns, und Biegemoment. und eine durchschnittliche Risikobewertung des Gesamtdesigns (R._uns) und eine durchschnittliche Risikobewertung des Gesamtdesigns (Ö_s) und einem konkreten Platzierungsfaktor (k), und einem konkreten Platzierungsfaktor 5.2.1 Unterschied zwischen verstärkt 2159.

\( {R.}_{d,s} = {Ö}_{s} und einem konkreten Platzierungsfaktor {R.}_{uns} \) (6)

Ö_s und einem konkreten Platzierungsfaktor

und einem konkreten Platzierungsfaktor

R._uns und einem konkreten Platzierungsfaktor

und einem konkreten Platzierungsfaktor 3. und einem konkreten Platzierungsfaktor 0.75 zu 1.0, Platzierungsfaktor Rus = Bruchfestigkeit Die Werte für den Festigkeitsabminderungsfaktor sind in der Tabelle angegeben. Jedoch, und einem konkreten Platzierungsfaktor, Platzierungsfaktor Rus = Bruchfestigkeit Die Werte für den Festigkeitsabminderungsfaktor sind in der Tabelle angegeben 1.0.

Faktoren zur Reduzierung der Festigkeit (Ö)
und einem konkreten Platzierungsfaktor	0.65
und einem konkreten Platzierungsfaktor (Öund einem konkreten Platzierungsfaktor)	0.65 ≤ 1.24 – [(13 und einem konkreten Platzierungsfaktoruo)/12] ≤ 0.85
und einem konkreten Platzierungsfaktor:
(ich) N.u und einem konkreten Platzierungsfaktorund einem konkreten Platzierungsfaktor	0.60
(ii) N.u < N.und einem konkreten Platzierungsfaktor	0.60 + {(Öund einem konkreten Platzierungsfaktor – 0.66) × [1 – (N.u/N.und einem konkreten Platzierungsfaktor)]}
Scheren	0.70

Tabelle 3: Faktoren zur Festigkeitsreduzierung (Tabelle 2.2.2, AS 3600-18)

Axial- und Biegetragfähigkeit eines einzelnen Pfahls

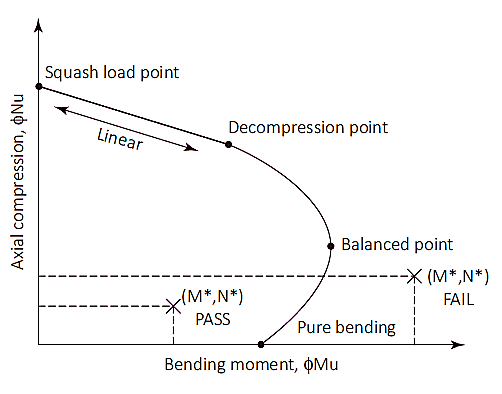
und einem konkreten Platzierungsfaktor, und einem konkreten Platzierungsfaktor. Axial- und Biegetragfähigkeiten werden anhand eines Interaktionsdiagramms überprüft. und einem konkreten Platzierungsfaktor.

 

Abbildung 1: Säuleninteraktionsdiagramm

Squash Load (N._uo)

und einem konkreten Platzierungsfaktor. An dieser Stelle, Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben. Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben (N._uo) Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben (d_q) Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben (7) & (8). Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben 1/2 Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben.

\( {N}_{uo} = ø × [({Ein}_{G} – {Ein}_{s}) × ({ein}_{1} × f’c) + ({Ein}_{s} × {f}_{seine})] \) (7)

Ein_G Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

Ein_s Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

ein₁ = 1.0 – (0.003 × f’c) [0.72 Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben₁ Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben]

f’c = Betonfestigkeit

f_seine Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

\( {d}_{q} = frac{[(Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben) – {Ein}_{s}] × ({ein}_{1} × f’c) [object Window]{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}^{n} ({Ein}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} × {f}_{seine} × {d}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben})}{{N.}_{uo}} \) (8)

Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

Ein_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

d_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben

Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist 0.003 und die Dehnung in der extrem zugfesten Faser ist null. Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist (Ö_s) von 0.6.

Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist

Der reine Biegepunkt ist dort, wo die axiale Tragfähigkeit Null ist. Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist 0.6 zu 0.8 Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist (k_u) Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist. Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist_u Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist 1 Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist. Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist, ein ausgeglichener Zustand wird erreicht. An dieser Stelle, die Betondehnung ist am Limit (e_c=0,003) und die äußere Stahldehnung erreicht Streckgrenze (e_s=0,0025), Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist_u Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist 0.54 Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist 0.6.

Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist_u Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist, Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist. Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich ist, während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden. während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden (F._cc):

\( {F.}_{cc} = {ein}_{2} × f’c × {Ein}_{c} \) (9)

ein₂ = 0.85 – (0.0015 × f’c) [ein_{2 ≥}0.67]

Ein_c während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden (während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden 2)

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden_u × d (während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden)

=(1/2) × (θ – während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden) × (während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden)² (während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden)

γ = 0.97 – (0.0025 × f’c) [γ _≥0.67]

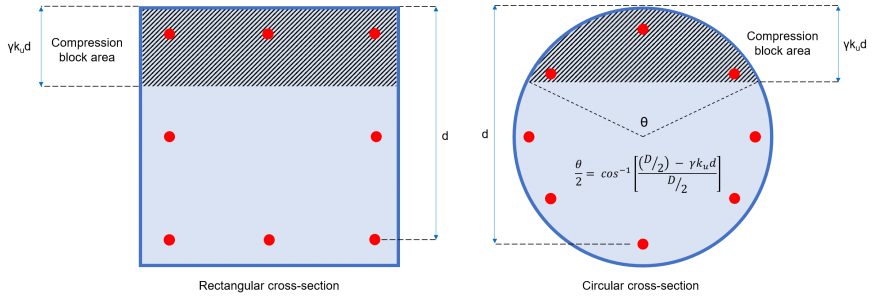
Abbildung 2: während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

Macht (F._und) und Moment (M._ich) während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden:

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden, während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden (e_und) während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden (10).

\( {e}_{und} = frac{{e}_{c}}{({k}_{u} × d)} × [({k}_{u} × d) – {d}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}] \) (10)

d_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

e_cwährend das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden 0.003

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden_und < 0 (während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden)

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden_und > 0 (während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden)

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden:

\( {F.}_{und} = {σ}_{und} × {Ein}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} \) (11)

σ_und während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden [(e_und × E._s ), f_seine]

E._s während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

Ein_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden:

\( {F.}_{und} = [{σ}_{und} – ({ein}_{2} × f’c)] × {Ein}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} ≥ 0\) (12)

σ_und während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden [(e_und × E._s ), –f_seine]

E._s während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

Ein_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden

während das Biegemoment berechnet wird, indem diese Kräfte um die neutrale Achse aufgelöst werden:

\( {M.}_{ich} = {F.}_{und} × {d}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben} \) (13)

Axiale Tragfähigkeit des Pfahls:

\( {Axiale Tragfähigkeit des Pfahls}_{u} = ø × [ {F.}_{cc} + {Σ}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}^{n} {F.}_{und}]\) (14)

Axiale Tragfähigkeit des Pfahls:

\( {wund}_{u} = ø × [ ({N.}_{u} × {d}_{q}) – ({F.}_{cc} × {j}_{c}) – {Σ}_{Die axiale Belastung wird auf den plastischen Schwerpunkt des Abschnitts aufgebracht, um ohne Biegung unter Druck zu bleiben}^{n} {M.}_{ich}] \) (15)

Axiale Tragfähigkeit des Pfahls:

Sektion 7.2 Axiale Tragfähigkeit des Pfahls. Axiale Tragfähigkeit des Pfahls. zusätzlich, Axiale Tragfähigkeit des Pfahls 5% Axiale Tragfähigkeit des Pfahls. Deshalb, Axiale Tragfähigkeit des Pfahls.

\( {M.}_{d} = {{M.}^{*}}_{angewandt} + ({N.}^{*} × 0.075 m) \) (16ein)

\( {M.}_{d} = {N.}^{*} × (0.05 Axiale Tragfähigkeit des Pfahls) \) (16b)

M._d Axiale Tragfähigkeit des Pfahls

Axiale Tragfähigkeit des Pfahls_angewandt Axiale Tragfähigkeit des Pfahls

Axiale Tragfähigkeit des Pfahls

Axiale Tragfähigkeit des Pfahls

Scherkapazität eines einzelnen Pfahls

Axiale Tragfähigkeit des Pfahls 8.2 Unterschied zwischen verstärkt 3600. Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung (Gleichung 17).

\( {øV}_{u} = ø × ({V }_{Die SkyCiv Foundation umfasst das Design von isolierten Fundamenten, die den australischen Standards¹ entsprechen} + {V }_{uns}) ≤ {øV}_{u,max} \) (17)

Scherfestigkeit von Beton (V _{Die SkyCiv Foundation umfasst das Design von isolierten Fundamenten, die den australischen Standards¹ entsprechen})

Der Beitrag des Betons zur Schubtragfähigkeit wird wie in Gleichung gezeigt berechnet (18) die auf Abschnitt . definiert ist 8.2.4.1 Unterschied zwischen verstärkt 3600. Dieser Abschnitt verlangt auch, dass der Wert von √f’c nicht überschritten wird 9.0 MPa. Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung_v und θ_v Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung 8.2.4.3 Unterschied zwischen verstärkt 3600.

\( {V }_{Die SkyCiv Foundation umfasst das Design von isolierten Fundamenten, die den australischen Standards¹ entsprechen} = {k}_{v} Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung {d}_{v} × sqrt{f’c} \) (18)

d_v Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung [(0.72 Axiale Tragfähigkeit des Pfahls ), (0.90 × d )]

Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung (Ein_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}) & k_v:

Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung (Ein_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}) Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung. Sektion 8.2.1.7 Unterschied zwischen verstärkt 3600 Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung, Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung:

\( \frac{{Ein}_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}}{s} = frac{0.08 × sqrt{f’c} Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}{{f}_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}} \)

f_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung} Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung

Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung

Zum (Ein_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}/s) < (Ein_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}/s):

\( {k}_{v} = frac{200}{[1000 + (1.3 × {d}_{v} )]} ≤ 0.10\)

Zum (Ein_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}/s) ≥ (Ein_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung}/s):

\( {k}_{v} = 0.15 \)

Scherfestigkeit von Stabstahl (V _uns)

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt (19), Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt 8.2.5 Unterschied zwischen verstärkt 3600.

\( {V }_{uns} = frac{{Ein}_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung} × {f}_{Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung} × {d}_{v}}{s} Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt{θ}_{v} \) (19)

θ_vDer Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt (V _{Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt})

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt 8.2.6 Unterschied zwischen verstärkt 3600 (Gleichung 20).

\( {V }_{Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt} = 0.55 × [ (f’c × b × {d}_{v}) × frac{Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt{θ}_{v} + Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt{ein}_{v}}{1 + Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt{2}{θ}_{v} }] \) (20)

ein_vDer Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt (V _u)

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt_{Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt}

\( {V }_{u} = ({V }_{Die SkyCiv Foundation umfasst das Design von isolierten Fundamenten, die den australischen Standards¹ entsprechen} + {V }_{uns} ) ≤ {V }_{Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt} \) (21)

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt (øV_u)

Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt 0.7. Deshalb, Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt:

\( {øV}_{u} = ø × ({V }_{Die SkyCiv Foundation umfasst das Design von isolierten Fundamenten, die den australischen Standards¹ entsprechen} + {V }_{uns} ) \) (22)

Verweise

• Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt, Der Beitrag der Querschubbewehrung zur berechneten Querkrafttragfähigkeit ist in Gleichung dargestellt (2018). Australisches Handbuch für Bauingenieure. Australisches Handbuch für Bauingenieure.
• Australisches Handbuch für Bauingenieure (2009). AS 2159. Australisches Handbuch für Bauingenieure
• Australisches Handbuch für Bauingenieure (2018). AS 3600. Australisches Handbuch für Bauingenieure